Общие методы решения конечных игр.
Приведение матричной игры к задаче линейного
Программирования
Мы рассматривали до сих пор только самые элементарные игры типа 2´m, которые могут быть весьма просто решены и допускают удобную и наглядную геометрическую интерпретацию.
В общем случае решение игры n´m представляет довольно трудную задачу, причем сложность задачи и объем необходимых для решения вычислений резко возрастает с увеличением n и m. Однако эти трудности не носят принципиального характера и связаны только с очень большим объемом расчетов, который в ряде случаев может оказаться практически невыполнимым. Принципиальная сторона метода отыскания решения остается при любом n и m одной и той же.
Проиллюстрируем это на примере игры 3´m. Дадим ей геометрическую интерпретацию - уже пространственную. Три наши стратегии А1, А2 и А3 изобразим тремя точками на плоскости х0у; первая лежит в начале координат (рис. 3.7), вторая и третья - на осях 0x и 0у на расстояниях 1 от начала.
III I II
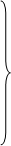
B1
B1
B1
a31 a11
0 (A1) a21
|
|
|
1
1 
(A3)
Y
(A2) X
III I II
Рис. 3.7.
Через точки А1, А2 и А3 проводятся оси I-I, II-II и III-III, перпендикулярные к плоскости х0у. На оси I-I откладываются выигрыши при стратегии А1, на осях II-II и III-III - выигрыши при стратегиях А2, А3. Каждая стратегия противника Bj изобразится плоскостью, отсекающей на осях I-I, II-II и III-III отрезки, равные выигрышам при соответствующих стратегиях А1, А2 и А3 и стратегии Bj.
Построив таким образом все стратегии противника, мы получим семейство плоскостей над треугольником A1, А2, А3 (рис. 3.8).
|
|
|
|
|
|
|
|
|
 | |||
 | |||
|
|
|
|
|
y
 |
(A3) (A2)
Y X
III I II
Рис. 3.8.
Для этого семейства также можно построить нижнюю границу выигрыша, как мы это делали в случае 2хm, и найти на этой границе точку N с максимальной высотой над плоскостью х0у. Эта высота и будет ценой игры n.
Частоты p1, р2, р3 стратегий A1, A2, А3 в оптимальной стратегии S*a будут определяться координатами (х, у) точки N, а именно: р2 = х; р3 = y; р1 = 1 - p2 - p3.
Однако, такое геометрическое построение даже для случая 3´m нелегко осуществимо и требует больших затрат времени и усилий воображения. В общем же случае игры оно переносится в n‑мерное пространство и теряет всякую наглядность, хотя употребление геометрической терминологии в ряде случаев может оказаться полезным. При решении игр n´m на практике удобнее пользоваться не геометрическими аналогиями, а расчетными аналитическими методами, тем более, что для решения задачи на вычислительных машинах эти методы единственно пригодны.
|
|
|
Вкратце остановимся на одном расчетном методе решения игр n´m - на применении метода линейного программирования.
Пусть игра n´m задана платежной матрицей A= аij ,i=1,n; j=1,m. Игрок А обладает стратегиями А1, A2,..., An, игрок В - стратегиями B1, B2,..., Bm. Необходимо определить оптимальные стратегии S*a= (p*1,p*2,..., p*n) и S*b = (q*1,q*2,..., q*m), где p*i, q*j - вероятности применения соответствующих чистых стратегий Ai, Bj;
Можно записать p*1+p*2+ ... +p*n = 1, q*1+q*2+ ... +q*m = 1.
Оптимальная стратегия S*a удовлетворяет следующему требованию. Она обеспечивает игроку А средний выигрыш, не меньший, чем цена игры n, при любой стратегии игрока В и выигрыш, равный цене игры n, при оптимальной стратегии игрока В. Без ограничения общности полагаем n>0, этого можно добиться, сделав все элементы аij >0. Если игрок А применяет смешанную стратегию S*a = (p*1,p*2,..., p*n) против любой чистой стратегии Bj игрока B, то он получает средний выигрыш, или математическое ожидание выигрыша aj = а1j·p*1+ a2j·p*2+ ... + аnj·р*n, j = 1,m (т.е. элементы j-го столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий A1, A2,..., An и результаты складываются).
|
|
|
Для оптимальной стратегии S*a все средние выигрыши не меньше цены игры n, поэтому получаем систему неравенств:
a11·p1 + a21·p2 + … + an1·pn ³ n a12·p1 + a22·p2 + … + an2·pn ³ n (3.6)
. . . . . . . . . . . . . . . . .
a1m·p1 + a2m·p2 + … + anm·pn ³ n
Каждое из неравенств можно разделить на число n>0. Введем новые переменные:
G1 = p1/n, G2 = p2/n, ..., Gn = pn/n (3.7)
Тогда система (3.6) примет вид:
a11·G1 + a21·G2 + … + an1·Gn ³ 1 a12·G1 + a22·G2 + … + an2·Gn ³ 1 (3.8)
. . . . . . . . . . . . . . . . .
a1m·G1 + a2m·G2 + … + anm·Gn ³ 1
Разделив на n¹0 равенство p1+p2+ ... +pn = 1, получаем, что переменные Gi (i =1,n) удовлетворяют условию: G1+G2+ ... +Gn = 1/n.
Цель игрока А - максимизировать свой гарантированный выигрыш, т.е. цену игры n. Максимизация цены игры n эквивалентна минимизации величины 1/n, поэтому задача может быть сформулирована следующим образом: определить значения переменных Gi³ 0, i=1,n, так, чтобы они удовлетворяли линейным ограничениям (3.8) и при этом линейная функция
Z = G 1 + G 2 + ... + G n (3.9)
обращалась в минимум.
Это задача линейного программирования. Решая задачу (3.8)-(3.9), получаем оптимальное решение p*1,p*2,...,p*n и оптимальную стратегию S*a.
При определении оптимальной стратегии 2-го игрока S*b=(q*1, q*2, ..., q*m) исходим из того, что средний проигрыш игрока В не превосходит цены игры, какую бы чистую стратегию не применял игрок А. То есть, переменные q1,q2,...,qm удовлетворяют неравенствам
a11·q1 + a12·q2 + … + a1m·q m≤ n a21·q1 + a22·q2 + … + a2m·q m≤ n (3.10)
. . . . . . . . . . . . . . . . .
an1·q1 + an2·q2 + … + anm·q m≤ n
Если обозначить Uj = qj/n, j =1, m (3.11)
то получим систему неравенств:
a11·U1 + a12·U2 + … + a1m·Um≤ 1 a21·U1 + a22·U2 + … + a2m·Um≤ 1 (3.12)
. . . . . . . . . . . . . . . . .
an1·U1 + an2·U2 + … + anm·Um≤ 1
Переменные Uj (j = 1, m) удовлетворяют условию
U1 + U2 + ... + Um = 1/n (из равенства q1+q2+...+ qm=1).
Если учесть, что игрок В стремится минимизировать гарантированный выигрыш, т.е. найти max(1/n), игра сведется к следующей задаче.
Определить значения переменных Uj≥0, j=1, m, которые удовлетворяют системе неравенств (3.12) и максимизируют линейную функцию
Z' = U1 + U2 + ... + Um (3.13)
Решение задачи линейного программирования (3.12), (3.13) определяет оптимальную стратегию S*b=(q*1, q*2, ..., q*m). При этом цена игры
n = 1/maxZ'= 1/minZ (3.14)
Составив расширенные матрицы для задач (3.8)-(3.9) и (3.12)-(3.13), убеждаемся, что:
- одна матрица получилась из другой транспонированием;
- знаки неравенств поменялись на противоположные;
- экстремумы линейных функций имеют противоположный смысл;
- свободные члены системы ограничений и коэффициенты линейных функций поменялись местами.
Таким образом, задачи линейного программирования (3.8)-(3.9) и (3.12)-(3.13) являются взаимно-двойственными. Очевидно, при определении оптимальных стратегий в конкретных задачах следует выбрать ту из взаимно-двойственных задач, решение которой менее трудоемко, а решение другой задачи найти с помощью теорем двойственности.
* * * * * *
Итак, с учетом вышеизложенного можно рекомендовать следующую схему решения произвольной конечной игры размера n×m:
1. Исключить из платежной матрицы заведомо невыгодные стратегии по сравнению с другими стратегиями. Такими стратегиями для игрока А являются те, которым соответствуют строки с элементами, заведомо меньшими по сравнению с элементами других строк. Для игрока В - столбцы с элементами, заведомо большими по сравнению с элементами других столбцов.
2. Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если седловая точка есть, то соответствующие ей чистые стратегии игроков будут оптимальными, а цена игры совпадает с верхней и нижней ценами.
3. Если седловая точка отсутствует, то решение следует искать в смешанных стратегиях. Для игр размера 2×2 возможно применение аналитического метода, для игр размера 2×2, 2×m, n×2 - геометрического или сочетания геометрического и аналитического методов решения, для игр размера n×m рекомендуется симплексный метод.
Дата добавления: 2018-09-22; просмотров: 316; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!