Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами и специальной правой частью
Для дифференциальных уравнений высших порядков с постоянными коэффициентами вида уравнения (11) существует более простой способ нахождения частного решения  , если правая часть имеет так называемый «специальный вид»:
, если правая часть имеет так называемый «специальный вид»:
 , ,
| (5) |
где  – постоянные,
– постоянные,  ,
,  – многочлены степени n и m соответственно.
– многочлены степени n и m соответственно.
Алгоритм построения частного решения неоднородного линейного дифференциального уравнения (2) следующий:
1. Найти корни характеристического уравнения (4).
2. Сравнить заданную правую часть уравнения (2) с общим видом выражения (5), при котором применим метод неопределенных коэффициентов, и найти из этого сопоставления три числа:  ,
,  .
.
3. Сравнить контрольное комплексное число  с корнями характеристического уравнения и найти число корней r, совпавших с этим комплексным числом (если таких корней нет, то r = 0).
с корнями характеристического уравнения и найти число корней r, совпавших с этим комплексным числом (если таких корней нет, то r = 0).
4. Записать частное решение неоднородного уравнения (2) в виде
 ,
,
где  и
и  – многочлены одной и той же степени l, но с неопределёнными и различными коэффициентами.
– многочлены одной и той же степени l, но с неопределёнными и различными коэффициентами.
5. Для нахождения неопределенных коэффициентов подставить записанное в п. 4 частное решение  в исходное уравнение и приравнять коэффициенты при одинаковых степенях переменной х. В результате получают систему уравнений, из которой находят значения неопределенных коэффициентов.
в исходное уравнение и приравнять коэффициенты при одинаковых степенях переменной х. В результате получают систему уравнений, из которой находят значения неопределенных коэффициентов.
Примечания:
1. Если правая часть уравнения (2) имеет более простой вид:  , то частное решение ищут в виде
, то частное решение ищут в виде  .
.
|
|
|
2. Правая часть уравнения может содержать только функцию вида  или функцию вида
или функцию вида  , но частное решение следует искать в полной форме, содержащей и
, но частное решение следует искать в полной форме, содержащей и  и
и  .
.
Пример 6. Найти общее решение уравнения 
Решение: общее решение уравнения будем искать в виде 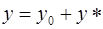 , где
, где  – общее решение соответствующего однородного уравнения
– общее решение соответствующего однородного уравнения  ,
,  – частное решение неоднородного уравнения.
– частное решение неоднородного уравнения.
Характеристическое уравнение  имеет корни
имеет корни  и
и  . Поэтому общее решение однородного уравнения имеет вид
. Поэтому общее решение однородного уравнения имеет вид  .
.
Частное решение неоднородного уравнения найдем методом неопределенных коэффициентов:
1. Корни характеристического уравнения  и
и  .
.
2.  , т.е.
, т.е.  ,
,  ;
; 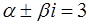 ,
,  и
и  – многочлены нулевой степени,
– многочлены нулевой степени,  .
.
3. Число 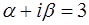 – корень характеристического уравнения кратности 1, поэтому r = 1.
– корень характеристического уравнения кратности 1, поэтому r = 1.
4. Частное решение следует искать в виде  .
.
5. Подставим  в исходное уравнение:
в исходное уравнение:
 ,
,  );
);
 ;
;
 ;
;
 ;
;  ;
;
 .
.
Общее решение исходного уравнения имеет вид  .
.
Ответ:  .
.
Пример 7. Решить уравнение  .
.
Решение: общее решение уравнения будем искать в виде  , где
, где  – общее решение соответствующего однородного уравнения
– общее решение соответствующего однородного уравнения  ,
,  – частное решение неоднородного уравнения.
– частное решение неоднородного уравнения.
Составим характеристическое уравнение:  , найдем его корни:
, найдем его корни:  и
и  . Общее решение однородного уравнения
. Общее решение однородного уравнения  имеет вид
имеет вид 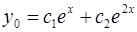 .
.
|
|
|
Частное решение неоднородного уравнения найдем методом неопределенных коэффициентов.
1. Корни характеристического уравнения  и
и  .
.
2.  ,
,  ,
,  ;
;  ;
;  ,
,  ;
;  ,
,  ;
;  .
.
3.  . Совпадений с корнями характеристического уравнения нет, следовательно, r = 0.
. Совпадений с корнями характеристического уравнения нет, следовательно, r = 0.
4. Частное решение исходного уравнения следует искать в виде  .
.
5. Подставим 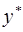 в исходное уравнение:
в исходное уравнение:
 =
=
=  ;
;
 =
=  ;
;
 +
+ 
 =
=  ;
;

 ;
;


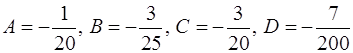 .
.
 .
.
Общее решение уравнения имеет вид  .
.
Ответ:  .
.
Дата добавления: 2018-09-20; просмотров: 168; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
