Предикаттар к лассификация сы
ДӘРІСТЕР ТЕЗИСТЕРІ 1 тақырып Жиындар теориясының элементтері Мақсаты: 1. Жиындар теориясының негізгі түсініктерін енгізу. 2. Жиындардың берілу тәсілдерін көрсету. 3. Жиындарға қолданылатын амалдарды және олардың негізгі қасиеттерін қарастыру. Жоспары : 1. Жиын. Ішкі жиын. Жиындардың берілу тәсілдері. 2. Жиындарға қолданылатын амалдар және олардың негізгі қасиеттері. 1 Жиын. Ішкі жиын. Жиындардың берілу тәсілдері Жиын түсінігі математиканың негізгі түсініктерінің бірі болып табылады. Бұл түсінікке қатаң түрде анықтама беруге болмайды. Жиындар теориясының негізін қалаған неміс математигі Георг Кантор (1845-1918) жиын түснігін келесі түрде анықтаған: «Бірнеше заттардың, объектілердің қандай да бір белгісіне қарай біртұтас болып бірігуі жиынды анықтайды». Кез келген жиындар A,B,C… үлкен латын әріптері арқылы белгіленеді. Жиынды құрайтын заттар (объектілер) оның элементтері деп аталады және а, b, c, … , x… кіші латын әріптерімен белгіленеді. М={x, y, z,…} жазуы М жиыны x, y, z,… элементтерінен тұрады дегенді білдіреді. а Î М – а элементі М жиынына тиісті, “Γ - тиістілік белгісі Егер жиынның құрамындағы элементтер саны ақырлы болса, онда жиын шектелген деп аталады, ал керісінше жағдайда шектелмеген деп аталады. 1 анықтама. Егер А жиынының әрбір элементі В жиынына тиісті болса, онда А жиыны В жиынының ішкі жиыны деп аталады, яғни , егер x Î A онда x Î В. Белгіленуі: А Í В- А жиыны B жиынының ішкі жиыны. Мысал . А={1,2} B={1,2,{1,3}} AÍB 2 анықтама . Құрамында бірде-бір элементі жоқ жиын бос жиын деп аталады және Æ белгіленеді. Берілген анықтамадан келесі қорытынды жасауға болады: 1. 1. Әрбір жиын өзінің ішкі жиыны болады, яғни 2. 2. Бос жиын кез келген жиынның ішкі жиыны болады, яғни Æ Универсал жиын деп, қандай-да бір берілген, анықталған, бізге белгілі жиынды атайды және U деп белгіленеді. Мысалы стереометрияда: кеңістіктегі барлық нүктелер жиыны . Алгебрада: Сандық жиындар үшін - C жиыны; элементар алгебрада – R жиыны. 3 анықтама . Құрамында бірдей элементтері бар екі жиын өзара тең деп аталады. Егер А жиынының кез келген элементі В жиынына тиісті болса және керісінше болса, яғни бір мезгілде 1)AÍB 2)BÍA екі шарт орындалса, онда А және В жиындары өзара тең болады. Екі жиынның теңдігі ескерту негізінде дәлелденеді.
|
|
|
Меншікті ішкі жиын.
|
|
|
4 анықтама. Егер А жиынының ішкі жиыны А жиынынан өзгеше және бос емес жиын болса, онда ол А жиынының меншікті ішкі жиын деп аталады. Анықтамадан Æ және берілген А жиынының өзі меншіксіз ішкі жиындар болып табылады.
Мысал. A = {a, b, c}
A жиынының 2 меншіксіз ішкі жиындары: Æ, A және 6 меншікті ішкі жиындары бар: {a}, {b}, {c}, {a,b}, {b,c}, {a,c}.
Жиындардың берілу тәсілдері
1) Жиын оның барлық элементтерін санау арқылы беріледі (тек қана ақырлы жиындар үшін қолданылады, оның өзінде бәріне емес).
A={x 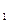 , x
, x 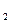 ,¼, x
,¼, x 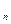 }
}
2) Жиынның элементтерінің сипаттамалық қасиеттерін көрсету арқылы:
2 Жиындарға қолданылатын амалдар.
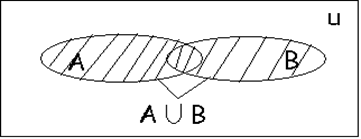
5 анықтама. А және В жиындарының бірігуі деп, элементтері А және В жиындарының кем дегенде біреуіне тиісті болатын жиынды атайды.
Белгіленуі: AÈB={x çxÎA немесе xÎB}.
Мысал. A={1,2,3} B={2,3,4}; AÈB={1,2,3,4}
Көрнекілік үшін Эйлера-Венн диаграммасын қолдану ыңғайлы .
|
|
|
6 анықтама. А және В жиындарының қиылысуы деп, элементтері бір мезгілде А және В жиындарына тиісті болатын жиынды атайды.
Белгіленуі: А ∩ В = {х | х ÎA және хÎB}
Мысал: А = {1, 2, 3} В = {1, 2, 3} А ∩ В = {2, 3}
U
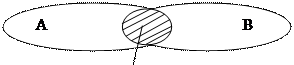 |
А ∩ В
Ç , È амалдарының қасиеттері :
3. Коммутативті: А È В = B È A; А Ç В = B Ç A
2. Ассоциативті: (А È В) È С = А È (В È С);
(А Ç В) Ç С = А Ç (В Ç С).
3. Дистрибутивті: А Ç (В È С) = (А Ç В) È (А Ç С)
А È (В Ç С) = (А È В) Ç (А È С).
4. Идемпотентті: А È A = A; А Ç A = A
5. А È Æ = A; А Ç Æ = Æ;
А È U = U; A Ç U = A.
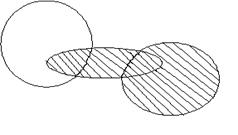
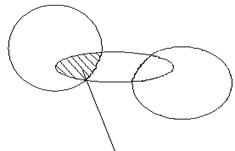
3 қасиетті диаграмма арқылы көрсетейік.
|

|
|
|
 U
U
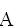 B A
B A
C B
C
A Ç (BÈC) (AÇB) È (AÇC)
7 анықтама. А және В жиындарының айырмасы деп, элементтері А жиынына тиісті, ал В жиынына тиісті емес жиынды атайды.
Белгіленуі: А \ В = {x | x Î A және x Ï B}.
Мысал: А = {1, 2, 3} В = {2, 3, 4}
А \ В = {1} В \ А = {4}
Бұл мысалдан азайту амалының коммутативті емес екендігі көрінеді.
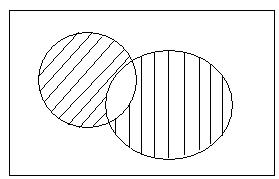
A U
B
A\B B\A
8 анықтама. B Í A жағдйына аса нзар аударайық.
Егер B Í A болса, онда A \ B = 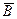 а айырмасы В жиынын А жиынына дейін толықтыру деп аталады.
а айырмасы В жиынын А жиынына дейін толықтыру деп аталады.
Мысал: В = {1, 3, 5} А = {1, 2,3,4,5} 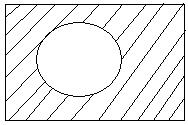
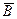 а = {2, 4}
а = {2, 4} 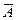 в = Æ
в = Æ
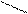
A
B 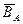
Жиі жағдайда А жиыны ретінде универсал U жиыны қарастырылады.
Белгіленуі: 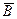 и =
и = 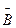
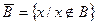
Азайту және толықтауыш амалдарының қасиеттері
6. А \ Æ = A; Æ \ А = Æ
7. Æ = U; 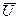 = Æ
= Æ
8. А Ç 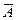 = Æ; А È
= Æ; А È 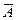 = U
= U
9. Де Морган заңдары: 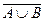 =
= 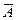 Ç
Ç 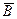 ;
; 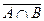 =
= 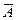 È
È 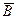
10. Инволюция заңы(екі рет терістеу): 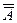 = А.
= А. 
Әдебиет : 1, 19-23 бет, 17, 69-83 бет, 3, 44-48 бет
Өзін-өзі тексеруге арналған сұрақтар:
1. Жиынның канторлық анықтамасын беріңіз және мысал келтіріңіз.
2. Қандай жиын бос, универсал деп аталады?
3. Қандай екі жиын өзара тең деп аталады?
4. Ішкі жиын дегеніміз не? Меншікті ішкі жиынды көрсету керек.
5. Жиындардың қандай берілу тәсілдері білесіз?
6. Жиындарға қолданылатын қандай амалдарды білесіз?
7. Жиындарға қолданылатын амалдардың қандай қасиеттері бар.
2 тақырып
Тура (декарт ты ) көбейтінді . Бейнелеулер
Мақсаты :
1. Декартты көбейтінді түсінігін енгізу.
2. Бейнелеулер, бейнелеудің мәндер жиыны түсініктерін енгізу.
3. Бейнелеудің түрлерін анықтау дағдысын қалыптастыру,
бейнелеудің композициясын таба білу.
Жоспары :
1. Жиындардың тура (декартты) көбейтіндісі.
2. Бейнелеулер, бейнелеудің түрлері, бейнелеудің композициясы.
1 Жиындардың тура (декарт ты ) көбейтіндісі
Біз жиындарға қолданылатын төрт амалды қарастырдық. Енді тағы да бір амал – жиындардың тура көбейтіндісін қарастырамыз.
А және В жиындары берілсін. <a,b> түріндегі барлық реттелген қостар жиынтығын қарастырамыз, мұндағы aЄA, bЄB. Белгілі бір ретте алынған екі элементті жиын реттелген қос деп аталады.
‹a, b› ≠ ‹b, a›
‹a, b› = ‹b, a›, егер a = b.
Қасиеті: ‹a, b› = ‹с, d› ↔ a = c, b = d
(Геометрияда: жазықтықтың кез келген нүктесі ‹x, y› - нүктенің координатасы деп аталатын екі сан арқылы бірмәнді анықталады, мұндағы бірінші сан х – абсцисса деп, ал екінші сан y – ордината деп аталады.)
1 анықтама. ‹x, y› түріндегі барлық реттелген қостар жиыны, мұндағы
x Є A, y Є B жиындардың тура (декартты) көбейтіндісі деп аталады.
Жазылу түрі: А´В = {‹x,y› | x Є A ^ y Є B}
Кез келген көрсетілген ретте алынған А және В жиындары үшін, олардың жалғыз түрде тура көбейтіндісі табылады: A´B=Ø <=> А=Ø ν B = Ø.
Егер A және B – ақырлы жиындар болса, онда A´B – ақырлы болады.
Мысал. А={-2,0,5} B={3,5}, A´B={(-2,3),(-2,5),(0,3),(0,5),(5,3),(5,5)}
Яғни А´B көбейтіндісінде 6 элемент бар.
Декартты көбейтінді түсінігінің геометриялық мағынасын қарастырайық.
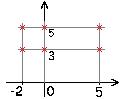 A´B жиынының геометриялық моделі.
A´B жиынының геометриялық моделі.
B´A={(3,-2),(3,0),(3,5),(5,-2),(5,0),(5,5)} табайық, яғни А´В ≠ B´A.
Осы мысалдан жиындардың тура көбейтіндісінің коммутативті емес екендігі көрінеді.
|A| арқылы ақырлы жиындағы элементтер санын белгілейік,
онда |А´В|=6.
Егер A – а1, … аn әртүрлі n элементтерден тұратын ақырлы жиын, ал В – b1, ... bm әртүрлі m элементтерден тұратын ақырлы жиын болса, онда A´B жиынының құрамында (a1,b1),(a1,b2), ... , (an,bm), ... , (an,bm) m*n әртүрлі элементтер бар=› |A´B|=|A|´|B|
Егер А және В жиындары өзара тең болса, онда А жиынын өзіне-өзін көбейту тура енемесе декартты квадрат деп аталады және A´A=А2 түрінде белгіленеді.
Анықталған ретте алынған үш элементтен тұратын жиын реттелген үштік деп аталады.
Үш жиынның тура көбейтіндісі ұғымын келесі түрде енгіземіз: A´B´С = {‹x, y, z› | x Є A, y Є B, z Є C}
Енді жазықтықтағы нүктелер жиынын R´R=R2 (нақты сандар жиыны) түріндегі тура көбейтінді ретінде көрсетеміз, ал кеңістіктегі нүктелер жиынын R´R´R=R3 түрінде көрсетеміз.
A1,A2, ... ,An n жиындар берілсін (әр түрлі болуы міндетті емес).
Реттелген қос түсінігінің жалпылауы n элементтен тұратын кортеж болады; ‹a1,a2, ... , an› түрінде белгіленеді және ұзындығы n – ге тең кортеж деп аталады.
2 анықтама. (a1,a2, ... , an), аi Є Ai (i=1, ... , n) түріндегі барлық реттелген кортеждер жиыны n жиынның тура көбейтіндісі деп аталады және келесі түрде белгіленеді A1´A2´..´An .
Сонымен: А1´A2´...´An= {‹a1,¼, an› | a1ЄA1, ... , anЄAn}.
Егер барлық Аi өзара тең болса, онда n-жиынның тура көбейтіндісі. А´A´…´A=Аn белгіленеді және А жиынының n дәрежесі деп аталады.
Егер А – ақырлы жиын және оның элементтерінің саны m – ге тең болса, яғни |A| = m болса, онда Аn жиынындағы элементтер саны mn болады. Дәлелдеуі:
|Аn| = |A´...´A| = |А|n = mn
Бейнелеулер
3 анықтама. Қандай да бір А жиынның әрбір элементін В жиынының тек қана бір элементімен салыстыратын f сәйкестігі A жиынын B жиынына бейнелеу деп аталады немесе В-дан мәндер қабылдайтын А анықталу облысы бар функция деп аталады.
Жазылу түрі: f: А®В
x®у = f (x), у – х элеметінің бейнесі,
х – у элементінің түпкі бейнесі.
f арқылы осы сәйкестік орнатылатын бейнелеуді (ережені ) белгілейді.
Венн диграммасы арқылы сәйкестік келесі түрде бейнеленеді.
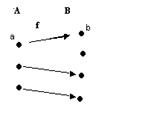
Сонымен, бейнелеуді (функцияны) үш жиын арқылы көрсетуге болады:
А, В және < x, y> A´B дан алынған барлық реттелген қостар жиыны, н мұндағы у = f (x).
3/ анықтама. Бейнелеу (функция) деп
<A,B,S > үштігі аталады, мұндағы S = {<x, y> Î A´B, y = f (x)}.
A – жиыны бейнелеудің анықталу облысы,
B – мәндер жиыны,
S – берілген бейнелеудің графигі.
Бейнелеудің түрлері
4 анықтама. Егер В жиынының әрбір элементі А жиынындағы бір ғана элементтің бейнесі болса, онда А жиынын В жиынына бейнелеу инъективті деп аталады.
Мысалы: х1¹х2 Þ f (х1) ¹ f (х2) " х1, х2 ÎA.
5 анықтама. Егер В жиынының әрбір элементі А жиынының кем дегенде бір элемнтінің бейнесі болса, онда А жиынын В жиынына бейнелеу сюръектив ті деп аталады.
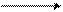

Инъекция Сюръекция
6 анықтама.Бір мезгілде сюръективті және инъективті болатын бейнелеу биективті бейнелеу немесе өзара бірмәнді сәйкестік деп аталады.
f бейнелеуі биектив ті деп аталады,егер кез-келген " bÎB А жиынындағы элементтің жалғыз бейнесі болса.


Бейнелеу емес. Бейнелеу емес.





инъекция, сюръекция емес жай бейнелеу
(инъекция емес, сюръекция емес)





Бейнелеу биекция
(сюръекция, инъекция емес)
7 анықтама. j:A®B, y:B®C бейнелеулері берілсін. f (x) = y (j (x)) формуласымен анықталған f:A®С бейнелеуі j, y бейнелеулерінің суперпозициясы (немесе композициясы) деп аталады.
Белгіленуі: y o j .
Кей-кезде суперпозиция көбейтінді деп аталады.
1) Бейнелеулердің суперпозиция операциясы ассоциативті:
j: А®В; y: B®C; f: A®C болсын
f o (y o j) = (f o j) o j
2) Бейнелеулердің суперпозиция операциясы коммутативті емес, яғни $ f, j: f o y ¹ y o f
j y
 A B C
A B C
 | |||
 | |||
y o j 
Әдебиет : 1, 38-39 бет; 152 бет; 2, 266 бет.
Бақылау сұрақтары :
1. Реттелген қос қалай анықталады?
2. Жиындардың тура (декартты) көбейтіндісі дегеніміз не?
3. Декартты квадрат қалай анықталады?
4. Жиындарды бейнелеу дегеніміз не?
5. Бейнелеудің қандай түрлерін білесіз?
6. Бейнелеудің композициясының анықтамасын айтыңыз.
6. тақырып
Бинар лық қатынастар . Фактор- жиын
Мақсаты :
1. Бинарлық қатынастар түсінігін енгізу және бинарлық
қатынастардың қасиеттерін қарастыру.
2. Эквивалентті және реттік қатынастар түсінігін енгізу.
3. Фактор-жиын түсінігін енгізу.
Жоспар:
1.Бинарлық қатынастар.Бинарлық қатынастардың негізгі қасиеттері.
2.Эквивалентті қатынас және кластарға бөлшектеу.
3. Реттік қатынас. Фактор-жиын.
1 Бинар лық қатынастар . Бинарлық қатынастардың негізгі қасиеттері
Математикада берілген жиынның элементтері арасындағы әртүрлі қатынастар зерттеледі. А жиынының әртүрлі қос элементтерін байланыстыратын қатынастарға тоқталамыз.
1 анықтама. Кез келген А және В жиындары үшін α 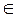 А´В ішкі жиыны А және В жиындарының элементтері арасындағы бинарлық қатынас деп аталады.
А´В ішкі жиыны А және В жиындарының элементтері арасындағы бинарлық қатынас деп аталады.
Егер А=В, онда α 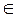 А2 А жиынында берілген бинарлық қатынас деп аталады.
А2 А жиынында берілген бинарлық қатынас деп аталады.
Егер реттелген қосы <а, в> 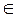 α болса, онда а және в α қатынасы арқылы байланысқан деп атайды, немесе, а элементі в элементімен α қатынасында деп айтады және а α в деп жазылады.
α болса, онда а және в α қатынасы арқылы байланысқан деп атайды, немесе, а элементі в элементімен α қатынасында деп айтады және а α в деп жазылады.
Мысал. А<в, а 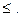 в, М нүктесі а түзуіне тиісті.
в, М нүктесі а түзуіне тиісті.
2 анықтама.Α бинарлық қкатынасының элементтерінің барлық бірінші координаталарының жиыны α қатынасының анықталу облысы деп аталады және 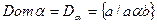 деп белгіленеді. Ал барлық екінші координаталарының жиыны α қатынасының мәндер жиыны деп аталады және
деп белгіленеді. Ал барлық екінші координаталарының жиыны α қатынасының мәндер жиыны деп аталады және 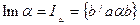 деп белгіленеді.
деп белгіленеді.
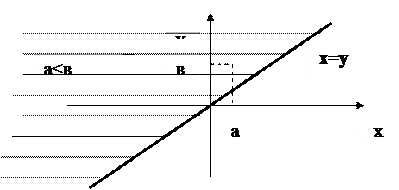
А жиыны- нақты сандар жиыны болған жағдайға аса назар аударамыз. Яғни А- R2 – кәдімгі жазықтық. Кез келген бинарлық қатынатар жазықтықтағы нүктелердің ішкі жиыны ретінде қарастырылады. Бұл сәйкес қатынастың көрнекі геометриялық сипаттамасын береді.
Мысал. Х<у қатынасы үшін орындалатын реттелген қостар жиыны у=х түзуінің жоғарғы бөлігінде орналасқан нүктелер жиыны.
 |
Жиындағы бинарлық қатынастардың қасиеттері
3 анықтама. А жиынындағы  бинарлық қатынас:
бинарлық қатынас:
а) рефлексивті деп аталады, егер А жиынының әрбір элементі өзімен - өзі 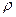 қатынаста болса.
қатынаста болса.
 - рефлексивті ó
- рефлексивті ó 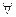 а
а 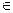 А а
А а  а.
а.
Мысалдар : =, 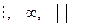 қатынастары
қатынастары
б) симметри ялы деп аталады , егер А жиынына тиісті кез келген а,в элементтері үшін а  в=>в
в=>в  а орындалса.
а орындалса.
 - симметриялы ó
- симметриялы ó 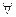 а, в
а, в 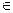 А а
А а  в=>в
в=>в 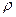 а.
а.
Мысалдар : =, 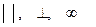 қатынастары
қатынастары
в) транзитив т деп аталадыі , егер А жиынына тиісті кез келген а,в,с элементтері үшін а  в
в 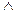 в
в  с => а
с => а  с
с
 - транзитивті ó
- транзитивті ó 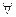 а, в, с
а, в, с 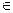 А а
А а  в
в 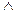 в
в 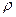 с => а
с => а 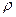 с.
с.
Мысалдар : <, 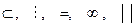 қатынастары
қатынастары
г) антирефлексив ті деп аталады, егер А жиынындағы бірде бір элемент өзімен-өзі 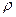 қатынасында болмаса.
қатынасында болмаса.
 - антирефлексивті ó
- антирефлексивті ó 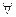 а
а 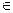 А а
А а  а.
а.
д) антисимметри ялы деп аталады, егер А жиынына бірмезгілде <а, в> және <в, а> қостары тиісті болмаса.
 - антисимметриялы ó
- антисимметриялы ó 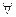 а,в
а,в 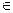 А а
А а  в
в 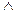 в
в  а => а = в немесе а
а => а = в немесе а 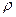 в
в 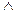 а
а 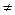 в => в
в => в 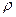 а.
а.
Мысалдар : 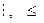 қатынастары
қатынастары
е) Байланысты деп аталады,егерА жиынының құрамына , әртүрлі а және в элементтері үшін немесе <а, в> қосы <в, а> болса.
 - байланысты ó
- байланысты ó 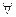 а,в
а,в 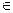 А а
А а 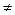 в => а
в => а  в
в 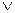 в
в 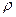 а.
а.
Мысалдар : <, 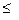 қатынастары
қатынастары
3 Эквивалентті қатынас және кластарға бөлшектеу
4 анықтама. А жиынында берілген  бинарлық қатынас рефлексивті, симметриялы және транзитивті болса, онда
бинарлық қатынас рефлексивті, симметриялы және транзитивті болса, онда  қатынасы А жиынында эквивалент ті қатынас деп аталады.
қатынасы А жиынында эквивалент ті қатынас деп аталады.
Белгіленуі ~.
Мысалдар: = , 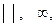
Кез келген жиында эквивалентті қатынастың берілуі кластарға бөлшектеу түсінігімен байланысты.
6. анықтама. А жиыныда оның Аi ішкі жиындарына бөлшектеу берілген дейміз, егер
1) барлық ішкі жиындар бос емес жиындар болса: Аi 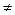 Ø
Ø 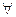 i
i 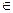 I;
I;
2) Әртүрлі екі ішкі жиын қиылыспаса
Аi 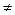 Aj => Ai
Aj => Ai 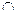 Aj = Ø
Aj = Ø 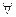 i,j
i,j 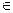 I;
I;
3) Барлық осындай ішкі жиындардың бірігуі А жиынын берсе :
UAi = A, i 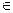 I.
I.
 - А жиынындағы бинарлық қатынас болсын.
- А жиынындағы бинарлық қатынас болсын.
{х | а  х} = ā
х} = ā 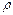 жиыны а элеметі тудыратын эквивалентті класс деп аталады.
жиыны а элеметі тудыратын эквивалентті класс деп аталады.
Мысалдар . А – үшбұрыштар жиыны, 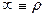 .
.
5 анықтама.  - А жиынындағы эквивалентті қатынас болсын, онда
- А жиынындағы эквивалентті қатынас болсын, онда 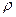 - ға қатысты барлық эквивалентті кластар жиыны А жиынының
- ға қатысты барлық эквивалентті кластар жиыны А жиынының 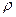 қатынасы бойынша фактор жиыны деп аталады және А/
қатынасы бойынша фактор жиыны деп аталады және А/  деп белгіленеді.
деп белгіленеді.
Әдебиет : 1, 34, 44 бет;
Бақылау сұрақтары :
1.Жиындағы бинарлық қатынас дегеніміз не?
2. Бинарлық қатынаста\ың қандай қасиеттері бар?
3. Бинарлық қатынастың мысалдарын келтіріңіз.
4. Эквивалентті қатынастың және кластарға бөлшектеудің анықтамасын беріңіз.
5. Реттік қатынас дегеніміз не?
6. Фактор-жиын қалай анықталады?
4. тақырып
Комбинаториканың э лемент тері .
Орын ауыстырулар
Мақсаты:
1. Комбинаторика түсінігін енгізу.
2. Комбинаториканың негізгі ережелерін қарастыру.
3. Орын ауыстыру түсінігін енгізу.
Жоспар:
1. Комбинаторика дискретті математиканың бөлімі.
2. Қосу және көбейту ережесі.
3. Қайталанатын және қайталанбайтын орын ауыстырулар.
5. Комбинаторика дискретті математиканың бөлімі.
Комбинаторика деп берілген шарт бойынша берілген объектілерден қанша әртүрлі комбинациялар құрауға болады деген сұрақты оқытатын математиканың бір бөлімі.
Көптеген практикалық жағдайларда анықталған шартты қанағаттандыратын объектілердің мүмкін болатын комбинациялар санын анықтау қажеттігі туады. Осындай есептер комбинаторлық деп аталады.
Комбинаторика 16 ғасырда пайда болды. Алғашқы кезде комбинаторика тек қана ойындарда қолданылып жүрді.
Комбинатормкалық есептер ықтималдықтар теориясында, математикалық логикада, сандар теориясында, есептеу техникасында, кибернетикада, экономикада, лингвистикада және т.б. қолданылады.
Комбинаторика – ықтималдық теориясында, математикалық логикада, комбинаторикада, есептеу техникасында, сандар теориясында қолданылуына байланысты маңызды орын алатын дискретті математиканың бір бөлімі.
6. Қосу және көбейту ережелері.
Комбинаторика есептерінің түрі әр типте болады. Көптеген есептер негізгі екі ереженің көмегі арқылы шешіледі. – қосынды және көбейту ережесі.
Мысал. Егер кітап сөресінің бірінші сөресінде 30 әртүрлі кітап болса, ал екіншісінде 40 әртүрлі кітап болса, онда бір кітапты таңдап алу 30+40=70 әдіс болады.
Қосу ережесі. Егер қандай да бір А объектіні m әдіспен таңдап алуға болса, ал B объектіні n әдіспен таңдап алуға болса, онда «немесе А, немесе В» таңдауын m+n әдіспен жүргізуге болады.
Мысал . Командир орнына 3 үміткер, ал бортмеханик орнына 2 үміткер бар. Қанша тәсілмен құрамында командир мен бортмеханик бар экипажды құруға болады?
Шешуі: Кемедегі командирді 3 тәсімен таңдап аплуға болады, командирді таңдағаннан соң ғана бортинженерді екі тәсілмен таңдауға болады. Жалпы тәсілдер саны көбейту ережесі бойынша 3*2=6 тең.
| ||||
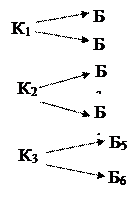 | ||||
Осындай сызба ағаш деп аталады.
Көбейту ережесі. Егер қандай да бір А объектіні m әдіспен таңдап алуға болса және осындай таңдаудан кейін ғана В объектісін n әдіспен таңдап алуға болса, онда (А, В) қосын көрсетілген ретте mn әдіспен таңдауға болады.
1 есеп. А қаласынан Б қаласына 2 жол бар, А қаласынан Г қаласына 4 жол бар, Б қаласынан В қаласына 3 жол бар, Г қаласынан В қаласына 5 жол бар.
А) А қаласынан Б қаласы арқылы В қаласына баратын қанша жол бар?
Б) А қаласынан В қаласына баратын қанша әртүрлі жол бар?
 Шешуі:
Шешуі:
а) Көбейту ережесі бойынша 2*3=6
б) 1 жағдай: Б арқылы: 6 жол
2 жағдай : Г арқылы: 4*5=20 жол
Қосынды ережесі бойынша 20+6=26 жол екенін аламыз.
2 есеп . 28 сүйектен тұратын доминодан қанша әдіспен екі сүйекті бір-біріне жалғап қоюға болатындай етіп, яғни екі сүйектегі ұпайлар саны бірдей етіп таңдауға болады.
Шешуі: алдымен бір сүйекті таңдап аламыз. Оны 28 әдіспен жүргізуге болады. 7 жағдайда сүйектердегі ұпайлар 00,11,22,33,44,55,66 болады. Ал 21 сүйектегі ұпайлар саны әртүрлі.
1 жағдай: екінші сүйекті 6 тәсілмен таңдауға болады, көбейту ережесі бойынша: 7*6=42 әдіс
2 жағдай: 2 сүйекті 12 әдіспен таңдауға болады және көбейту ережесі бойынша: 21*12=252 әдіс.
Қосу ережесі бойынша : 42+252=294 әдіс болады.
3 Қайталанатын және қайталанбайтын орын ауыстырулар.
{a1,…,an} n әртүрлі элементтерден тұратын жиын берілсін.
1 анықтама. К көлемді таңдау деп құрамында алғашқы элементтер бар {ai1,…,aik} жиыны аталады.
2 анықтама. Орналасу реті маңызды, ал элементтері бірдей болуы мүмкін болатын таңдаулар қайталанатын орынауыстыру деп аталады.
Белгіленуі: Аnk
|
7. анықтама. Барлық элементтері әртүрлі, орналасу реті маңызды болатын таңдаулар қайталанбайтын орын ауыстыру деп аталады. Белгіленуі: Ank
|
1 ден n-ге дейінгі барлық натурал сандардың көбейтіндісі n! Деп белгіленеді, яғни n!=1.2…n
Анықтама бойынша егер k>n болса, An0=1; Ank=0 деп есептеледі.
Әдебиет: 1, 134-136бет; 20; 10,9-21 бет
Бақылау сұрақтары:
1. Комбинаторика нені оқытады?
2. Комбинаториканың қандай негізгі ережелерін білесіз?
3. Қайталанатын орын ауыстыру қалай анықталады?
4. Қайталанбайтын орын ауыстыру қалай анықталады?
5. Оларды табу формулаларын жазыңыз.
5 тақырып
Алмастырулар және терулер
Мақсаты :
1. Қайталанатын және қайталанбайтын алмастырулар түсінігін енгізу.
2. Қайталанатын және қайталанбайтын терулер түсінігін енгізу.
Жоспар :
1. Қайталанатын және қайталанбайтын алмастырулар.
2. Қайталанатын және қайталанбайтын терулер.
1 Қайталанатын және қайталанбайтын алмастырулар
1 анықтама. k=n болғандағы қайталанбайтын орын ауыстыру алмастыру деп аталады. (Мұндай таңдаулар тек қана элементтеріның реті бойынша ажыратылады).
Белгіленуі: Pn
|
Теорема.
Дәлелдеуі: Pn=Ann= n (n-1)…(n-(к-1))=n!
0! =1 деп есептеледі.
Мысал. Морзе әліппесінің әріптері нүктелер тізбегі және тире арқылы құрылады. 5 символдан тұратын код арқылы қанша әртүрлі әріптер құруға болады?
Шешуі: Берілген жиын 2 элементтен тұрады: нүкте, тире. 5 символ қолданылады, сондықтан таңдауда қайталануы мүмкін 5 элемент бар. Демек, таңдаулар саны 25=32=А25
Мысал. 11 адамнан тұратын футбол командассымен қанша тәсілмен капитанды және қақпашыны таңдап алуға болады?
Шешуі: 11 футболисттің әрқайсысы капитан бола алады. Оны таңдағаннан кейін қақпашының орнына қалған 10 адам болуы мүмкін. Ендеше 11*10=110=А112 таңдаудың әртүрлі саны.
Мысал. Бір қатарға неше тәсілмен қызыл, қара, көк және жасыл шарларды қоюға болады?
Шешуі. 1-ші орынға 4 шардың кез келгенін қоюға, 2-ші орынға қалған 3 шардың кез келгенін, ал 3-ші –қалған 2-ң кез ккелгенін, 4-ші орынға– соңғы қалған шарды қоюға болады.
4!=24=P4
2 Қайталанатын және қайталанбайтын терулер
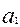 элементі
элементі 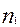 рет,
рет, 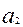 -
- 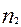 ,
, 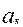 -
- 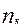 рет кіретін А= {
рет кіретін А= { 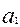 ,
, 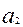 ,…,
,…, 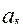 } жиынынан келесі таңдауларды қарастырамыз. Онда жалпы таңдау көлемі: m=
} жиынынан келесі таңдауларды қарастырамыз. Онда жалпы таңдау көлемі: m= 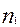 +
+ 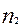 + …+
+ …+ 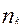 .
.
( 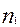 ,…,
,…, 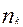 ) натурал сандар жиынтығын таңдаудың құрамы деп атайды.
) натурал сандар жиынтығын таңдаудың құрамы деп атайды.
2 анықтама.Бір құрамның әртүрлі таңдаулар саны m элементтен тұратын 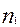 ,… ,
,… , 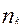 қайталау саны берілген алмастыру деп аталады.
қайталау саны берілген алмастыру деп аталады.
Мысал . Бұл сан мынау формуламен есептеледі: 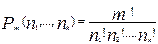 .
.
Дәлелдеуі: Расында да, егер барлық m элементтер әртүрлі болса, онда алмастырулар саны m ! болар еді. 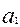 элементі
элементі 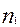 рет кіргендіктен, онда осы элементті алмастыру жаңа алмастыру бермейді =>
рет кіргендіктен, онда осы элементті алмастыру жаңа алмастыру бермейді => 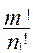 әртүрлі алмастырулар саны және т.с.с.
әртүрлі алмастырулар саны және т.с.с.
Есеп . «МАТАМАТИКА» сөзінің әріптерінен қанша әртүрлі сөздер құруға болады?
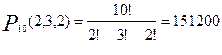 .
.
3 анықтама. Барлық элементтері әр түрлі, ал орналасу реті маңызды емес таңдаулар n элементтен k бойынша алынған терулер (қайталанбайтын) деп аталады.(Осындай таңдаулар ретімен емес, тек қана құрамы бойынша ажыратылады)
Теорема. 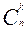 =
= 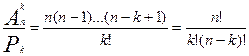 .
.
Дәлелдеуі: әрбір теруден k! Алмастыру құруға болады, ал осындай терулер саны 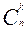 және көбейту ережесі бойынша
және көбейту ережесі бойынша
k!· 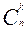 =
= 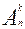 болады.
болады.
Есеп . Елде әрбір екеуі авиажол арқылы 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране?
Шешуі. Әрбір авиажол 2 қаланы байланыстырады. 1-ші қала ретінде 20 қаланың кез келгнін алуға болады (А қаласы), ал 2-ші қала ретінде қалған 19-дың кез келгенін алуға (В қаласы). Осы сандарды көбейтіп 20·19=380 аламыз. Бірақ әрбір санауда авиажол екі рет қайталанады. Ендеше авиажолдар саны 380:2=190= 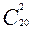 .
.
4 анықтама. Бірдей элементті k топтан құрылған құрамы әртүрлі n көлемді таңдаудың саны. k элемент бойынша n-н құрылған теру (қайталанатын) деп аталады. 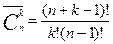
Әдебиет: 1, 136-142 бет; 15-20 бет; 10, 31-51 бет
Бақылау сұрақтары:
1. Қайталанатын және қайталанбайтын алмастырулардың анықтамасын беріңіз.
2. Қайталанатын және қайталанбайтын терулердің анықтамасын беріңіз.
3. Оларды табу формулаларын жазыңыз.
6 тақырып
Z сақинасындағы бөлінгіштік қатынасы
Мақсаты :
1. Z сақинасындағы бөлінгіштік қатынасын қарастыру.
2. ЕҮОБ және ЕКОЕ түсініктерін енгізу, олардың арасындағы байланыс.
3. Практикалық есептер шығарудағы біліктілік пен дағдыны қалыптастыру.
Жоспар :
1. Бөлінгіштік қатынасы, оның қарапайым қасиеттері.
2. ЕҮОБ. Евклид алгоритмі. ЕКОЕ.
3. Жай сандар.
Сандар теориясы 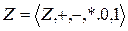 бүтін сандардың қасиеттерін қарастырады.
бүтін сандардың қасиеттерін қарастырады.
1 Бөлінгіштік қатынасы, оның қарапайым қасиеттері
1 аны0тама . Егер a=b*q шартын қанағаттандыратын бүтін q саны табылса, онда а бүтін саны b бүтін санына бөлінеді дейміз.
а – бөлінгіш, b – бөлгіш, q – бөлінді.
Б өлінгіштік қатынасының қасиеттері .
10 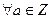 бөлінгіштік қатынасы рефлективті.
бөлінгіштік қатынасы рефлективті. 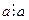 (так как а=а*1, 1
(так как а=а*1, 1 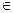 Z) .
Z) .
20 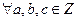 бөлінгіштік қатынасы транзитивті.
бөлінгіштік қатынасы транзитивті. 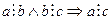
( 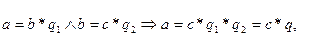
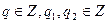 ).
).
30 Кез-келген а сыны 1-ге бөлінеді. 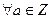 (а=1*а).
(а=1*а).
40 Егер 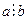 , онда
, онда 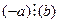 ,
, 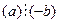 және
және 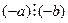 . Бөлінгіштің де, бөлгіштің де таңбалары өзгергенде бөлінгіштік қатынасы сақталады.
. Бөлінгіштің де, бөлгіштің де таңбалары өзгергенде бөлінгіштік қатынасы сақталады.
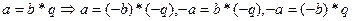 , мұндағы
, мұндағы 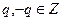 .
.
50 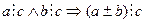
( 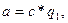
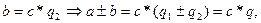
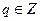 )
)
60 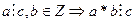
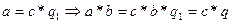 , мұндағы
, мұндағы 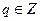 ( ассоциативті, коммутативті болғандықтан).
( ассоциативті, коммутативті болғандықтан).
70 (50,60 қасиеттерден шығады) 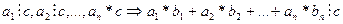 ,
, 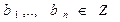 .
.
80 Егер 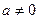 болса, онда 0*
болса, онда 0* 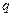 =а шартын қанағаттандыратын
=а шартын қанағаттандыратын 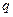 саны табылмайды.
саны табылмайды.
Қысқаша айтқанда, нөлге бөлуге болмайды.
90 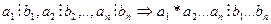
( 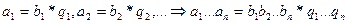 ,
, 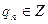 ).
).
100 (90 қасиеттің салдары) 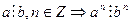
( 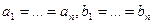 болғанда, дербес жағдай).
болғанда, дербес жағдай).
110 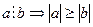 ,
, 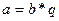 , себебі
, себебі 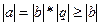 .
.
120 (110 қасиеттің салдары ) 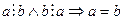 немесе
немесе 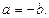
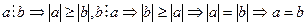 немесе
немесе 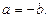
Қалдықпен бөлу .
Анықтама. Егер келесі екі шарт орындалатындай 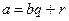 ,
, 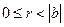 ,
, 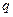 және
және 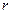 сандары табылса, онда а бүтін саны
сандары табылса, онда а бүтін саны 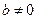 бүтін санына қалдықпен бөлінеді дейміз.
бүтін санына қалдықпен бөлінеді дейміз. 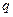 - бөлінді,
- бөлінді, 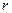 - қалдық.
- қалдық.
Теорема. а және 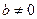 бүтін сандары қандай болса да а санын b санына қалдықпен бөлуге болады және бір ғана тәсілмен.
бүтін сандары қандай болса да а санын b санына қалдықпен бөлуге болады және бір ғана тәсілмен.
Дәлелдеуі:
I. Алдымен қалдықпен бөлу мүмкіндігін дәлелдейміз.
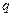 және r табылуы.
және r табылуы.
а) 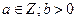 .
.
b -ға еселі барлық бүтін сандарды қарастырып, өспелі түрде орналастырамыз. …, b*(-2), b*(-1), b*0, b*1, b*2, …
bq – a –дан аспайтын, b –ң ең үлкен еселігі болсын.
Онда 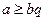 , бірақо
, бірақо 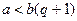 , яғни
, яғни 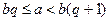 , осыдан
, осыдан 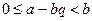 .
.
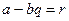 деп алып,
деп алып, 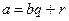 ,
, 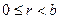 екенін аламыз.
екенін аламыз.
б) 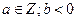 болсын.
болсын.
b<0 болғандықтан, –b>0 . Ендеше а) жағдайына қатысты а саны –b-ға бөлінеді, q және r бүтін сандары табылады.
Демек 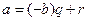 ,
, 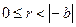 немесе
немесе 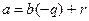
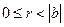
II. q мен r жалғыздығы.
Кері жоримыз.
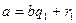
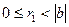
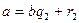
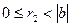 болсын.
болсын.
Яғни екі 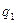 мен
мен 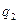 және
және 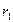 мен
мен 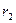 табылады. .
табылады. .
Онда 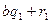 =
= 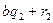
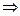
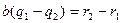 …(*)
…(*)
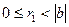 ,
, 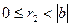 болғандықтан
болғандықтан 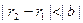
Басқа жағынан алғанда 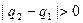
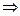
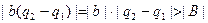
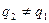 – қайшылыққа келдік
– қайшылыққа келдік 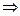
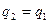
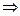
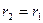
2 ЕҮОБ. Евклид алгоритмі. ЕКОЕ.
3 анықтама. 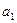 , ... ,
, ... , 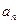 сандарының әрқайсысын да бөлетін
сандарының әрқайсысын да бөлетін 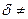 0 бүтін санын олардың ортақ бөлгіші деп аталады.
0 бүтін санын олардың ортақ бөлгіші деп аталады.
4 анықтама. Егер келесі екі шарт орындалса:
1) 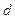 бүтін саны
бүтін саны 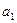 , ... ,
, ... , 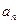 сандарының ортақ бөлгіші болса;
сандарының ортақ бөлгіші болса;
2) 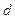

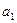 , ... ,
, ... , 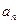 сандарының кез-келген ортақ бөлгішіне бөлінсе;
сандарының кез-келген ортақ бөлгішіне бөлінсе;
онда 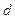 бүтін саны осы сандардың ең үлкен ортақ бөлгіші деп аталады.
бүтін саны осы сандардың ең үлкен ортақ бөлгіші деп аталады.
Қысқаша ЕҮОБ және 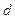 = (
= ( 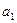 , ... ,
, ... , 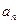 ) деп белгіленеді.
) деп белгіленеді.
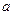 және
және 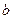 сандары үшін (
сандары үшін ( 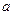 ,
, 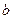 ) =
) = 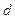 .
.
Евклид алгоритмі
Лемма 1. Егер 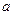
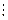
 , онда (
, онда ( 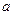 ,
,  ) =
) = 
Дәлелдеуі: 1) 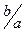 и
и 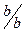
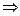
 -
- 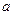 және
және  ортақ бөлгіші.
ортақ бөлгіші.
2) 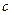 -
- 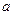 және
және  ортақ бөлгіші болсын.
ортақ бөлгіші болсын.
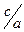 ,
, 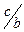
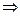
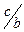
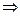
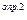 (
( 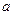 ,
,  ) =
) =  .
.
Лемма 2. Егер 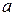 =
= 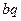 +
+ 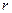 , мұндағы a , b ,
, мұндағы a , b , 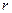 нөлден өзгеше сандар, онда (
нөлден өзгеше сандар, онда ( 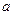 ,
, 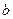 ) = (
) = ( 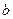 ,
, 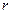 ).
).
Евклид алгоритмі екі санның ЕҮОБ табу үшін қолданылады.
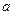 және
және  - оң сандар болсын,
- оң сандар болсын, 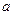 >
>  >0.
>0.
Алдымен 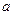 санын
санын  санына бөлеміз, егер
санына бөлеміз, егер 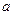
 -ға бөлінсе, онда 1 лемма бойынша
-ға бөлінсе, онда 1 лемма бойынша 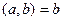 , ал егер
, ал егер 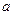
 -ға бөлінбесе, онда қалдықпен бөлу теоремасы бойынша
-ға бөлінбесе, онда қалдықпен бөлу теоремасы бойынша 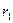 қалдық аламыз:
қалдық аламыз: 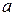 =
= 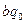 +
+ 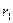 , 0
, 0 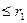 <
<  .
.
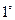 .
. 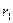 =0, яғни
=0, яғни 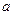
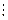

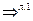
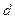 =
=  .
.
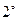 .
. 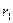
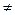 0, онда келесі теңдіктерді аламыз.
0, онда келесі теңдіктерді аламыз.
 =
= 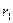
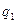 +
+ 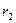 ; 0 <
; 0 < 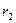 <
< 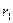 (егер
(егер 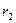 =0, онда процесс аяқталады).
=0, онда процесс аяқталады).
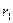 =
= 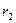
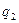 +
+ 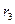 0<
0< 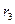 <
< 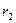
- - - - - - - - - - - - - - - - - - - - - -
(I) 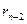 =
= 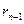
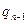 +
+ 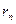 0<
0< 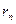 <
< 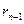
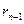 =
= 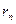
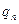
Біз 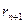 =0 алған кезде бұл процесс аяқталады.
=0 алған кезде бұл процесс аяқталады.
Бөлу процесінде шыққан сандар натурал болғандықтан және кемімелі болғандықтан, қандай-да бір қадамда қалдықсыз бөлу аламыз.
2 лемма бойынша: ( 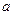 ,
,  ) = (
) = (  ,
, 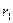 ) = (
) = ( 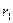 ,
, 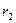 ) = …= (
) = …= ( 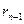 ,
, 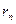 ) =
) = 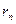 .
.
Қорытынды: Ең соңғы нөлден өзгеше қалдық а және в сандарының ЕҮОБ болып табылады.
Мысал. 185 және 5 сандарының ЕҮОБ табу керек.
(185, 55)= 5.
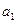 , ... ,
, ... , 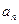 сандар жиынының ЕҮОБ табу есебі екі санның ЕҮОБ табу болып табылады..
сандар жиынының ЕҮОБ табу есебі екі санның ЕҮОБ табу болып табылады..
1 т еорема . Егер ( 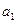 ,
, 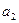 )=
)= 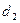 ; (
; ( 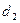 ,
, 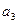 )=
)= 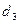 , … , (
, … , ( 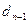 ,
, 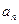 )=
)= 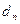 , онда
, онда
( 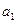 , ... ,
, ... , 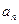 )=
)= 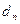 .
.
ЕҮОБ қасиеттері .
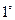 .
. 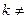 0,
0, 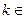 Z болсын.
Z болсын.
Онда ( 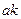 ,
, 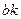 )= (
)= ( 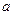 ,
,  )
) 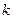
Евклид алгоритмін қолданамыз 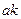 =
= 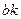
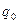 +
+ 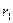
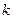
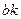 =
= 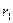
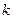
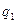 +
+ 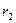
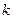
- - - - - - - - - - - -
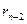
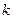 =
= 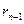
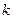
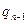 +
+ 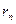
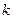
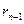
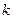 =
= 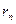
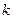
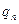
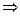 (
( 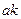 ,
, 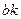 )=
)= 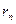
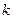 = (
= ( 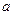 ,
,  )
) 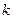 .
.
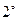 .
. 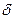 -
- 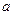 және
және  сандарының кез келген ортақ бөлгіші болсын, онда
сандарының кез келген ортақ бөлгіші болсын, онда
( 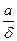 ;
; 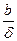 )=
)= 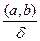
( 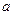 ,
, 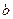 )= (
)= ( 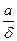
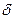 ;
; 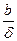
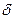 )= (
)= ( 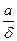 ;
; 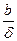 )
) 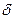
ЕКОЕ
5 анықтама. 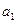 , ... ,
, ... , 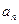 - нөлден өзгеше бүтін сандар болсын. Егер
- нөлден өзгеше бүтін сандар болсын. Егер 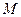
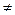 0 бүтін саны берілген сандардың әрқайсысына бөлінсе,онда осы сандардың ортақ еселігі деп талады.
0 бүтін саны берілген сандардың әрқайсысына бөлінсе,онда осы сандардың ортақ еселігі деп талады.
6 анықтама. Егер 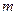 бүтін саны
бүтін саны 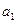 , ... ,
, ... , 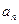 сандарының
сандарының
1) ортақ еселігі болса;
2) кез- келген ортақ еселік 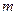 -ге бөлінсе;
-ге бөлінсе;
онда 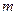 -
- 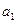 , ... ,
, ... , 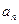 сандарының ең кіші ортақ еселігі деп аталады.
сандарының ең кіші ортақ еселігі деп аталады.
ЕКОЕ табу тәсілі, ЕКОЕ пен ЕҮОБ арасындағы байланыс.
Теорема. 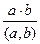 саны, мұндағы (a,b)=d - a және b сандарының ең кіші ортақ еселігі болып табылады.
саны, мұндағы (a,b)=d - a және b сандарының ең кіші ортақ еселігі болып табылады.
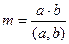 .
.
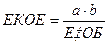
Жай сандар
1 анықтама . Егер p натурал саны 1-ден үлкен болса және 1 мен p –дан өзге оң бөлгіштері болмаса, онда p натурал саны жай сан деп аталады.
2 анықтама. Егер n натурал саны 1-ден үлкен болса және 1 мен n –нен өзге ең болмағанда бір оң бөлгіші бар болса, онда n натурал саны құрама сан деп аталады.
1 жай сан да, құрама сан да емес.
Натурал қатардағы алғашқы жай сандар: 2, 3, 5, 7, 11, 13, …
Жай сандардың арасында жалғыз жұп сан – 2.
Сонымен натурал сандар жиынының 3 ішкі жиыны бар: жай сандар, құрама сандар, 1 саны.
Жай сандардың қасиеттері :
1. Егер p жай саны қандай да бір n 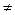 1 натурал санға бөлінсе, онда p=n .
1 натурал санға бөлінсе, онда p=n .
Дәлелдеуі: p 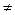 n болсын
n болсын 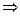 p санының үш бөлгіші болушы еді: 1, p, n.
p санының үш бөлгіші болушы еді: 1, p, n.
Берілгені бойынша p жай сан, ендеше бұлай болуы мүмкін емес.
2. Егер p1мен p2 –әртүрлі жай сандар болса, онда p2 саны p1 ге бөлінбейді.
Дәлелдеуі: p2 – жай сан, онда p2-нің бөлгіштері 1 және p2 өзі болады. Шарт бойынша p2 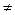 p1 , ал анықтама бойынша p1
p1 , ал анықтама бойынша p1 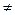 1. Демек p2 саны p1 ге бөлінбейді.
1. Демек p2 саны p1 ге бөлінбейді.
3. Егер n 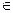 N сан, ал p – жай сан болса, онда n саны p –ға бөлінеді немесе n мен p өзара жай болады.
N сан, ал p – жай сан болса, онда n саны p –ға бөлінеді немесе n мен p өзара жай болады.
Дәлелдеуі: (p, n)= d болсын 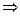
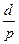 p- жай сано
p- жай сано 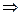 d= 1 немесе d = p, d = 1
d= 1 немесе d = p, d = 1 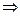 (d, n)
(d, n) 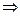 1; d = p
1; d = p 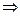 n
n 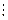 d, т.е. n
d, т.е. n 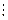 p
p
4. Егер екі немесе бірнеше натурал сандардың көбейтіндісі p жай санға бөлінсе, онда көбейткіштердің кемінде біреуі p – ға бөлінеді.
Яғни ab 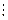 p
p 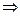 a
a 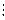 p
p 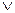 b
b 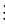 p
p
Дәлелдеуі: егер a 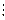 p – онда теореманың шарты тура болады, ал егер
p – онда теореманың шарты тура болады, ал егер
саны a p-ға бөлінбесе 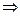 (a, p) = 1
(a, p) = 1 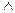 ab
ab 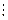 p
p 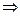 b
b 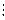 p
p
Теорема 1. Кез келген n>1 натурал саны кем дегенде бір жай санға бөлінеді.
Теорема 2. Егер n натурал саны құрама сан болса, ал p – оның жай бөлгіші болса, онда 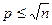 .
.
Осы теорема арқылы натурал сан жай ма әлде құрамас сан ба анықтауға болады.
Жай сандар тізбегі шексіз. Бұл қорытынды 9 ғасырда Евклидтің “Бастамаларында” 20 теорияда айтылған болатын.
Евклида т еорема сы. Жай сандар жиыны шексіз.
Жай сандар шексіз болса да, барлық натурал сандардың көп бөлігін құрамайды.
Әдебиет : 8, 8-16 бет, 16, 7-18 бет
Бақылау сұрақтары :
1. Қалдықпен бөлу туралы теореманы айтыңыз.
2. Безу теоремасын айтыңыз.
3. Екі санның ЕҮОБ дегеніміз не?
4. ЕҮОБ қасиеттерін санап шығыңыз.
5. Евклид алгоритмінің мағынасы неде және ол екі санның ЕҮОБ табуда қалай қолданылады?
6. Екі санның ЕКОЕ дегеніміз не?
7. Қандай сандар жай сандар, құрама сандар деп аталады?
8. Екі санның ЕҮОБ және ЕКОЕ қандай формула байланыстырады?
9. Жай сандар жиыны ақырлы ма?
7 тақырып
Z сақинасындағы салыстырулар
Мақсаты :
1. Z сақинасындағы салыстырулар қатынасын қарастыру.
2. Қалындылардың толық және келтірілген жүйесі түсінігін енгізу.
3. Эйлер және Ферма теоремаларын дәлелдеу.
4. Практикалық есептер шығаруда дағды мен біліктілікті қалыптастыру.
Жоспар :
1. Салыстырулар қатынасы, салыстырулардың қасиеттері.
2. Қалындылардың толық және келтірілген жүйесі.
3. Эйлер функциясы. Эйлер және Ферма теоремалары.
4. Бір белгісізі бар бірінші дәрежелі салыстырулар.
Салыстырулар қатынасы, салыстырулардың қасиеттері
1 анықтама . m – натурал сан болсын. Егер а-в айырмасы m санына бөлінетін болса, онда а мен в бүтін сандары m модулі бойынша салыстырымды деп аталады.
Жазылу түрі a ≡ b (mod m). Оқылу түрі «а саны в санымен m mod бойынша салыстырымды ».
2 анықтама. Егер а және в бүтін сандарының m-ге бөлгендегі қалдықтары бірдей болса, онда а және в сандары m модулі бойынша салыстырымды деп аталады.
Сөйлем . 1 – 2 анықтамалар мәндес.
Салдарлар.
1. a 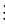 m ó a ≡ 0 (mod m)
m ó a ≡ 0 (mod m)
m –ге еселі кез келген сан, m модулі бойынша салыстырымды.
2. a =mg + r ó a ≡ r (mod)
0 ≤ r < m
Кез келген бүтін сан m –ге бөлгендегі r қалдықпен, m модулі бойынша салыстырымды.
Салыстырудың қасиеттері.
10. рефлексивті: а ≡ а (mod m) а Є Z
a – a = 0 m
20. симметриялы: а ≡ b (mod m) => b ≡ а (mod m)
a – b 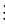 m => b – a
m => b – a 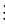 m
m
30. транзитивті: а ≡ b (mod m) Λ b ≡ c (mod m) => a ≡ c (mod m)
a – b 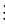 m Λ b – c
m Λ b – c 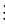 m => (a – c) + (b – c) =a – c
m => (a – c) + (b – c) =a – c 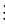 m
m
Қорытынды . Z жиынындағы m модулі бойынша салыстыру қатынасы – эквивалентті қатынас болады => Z жиыны өзара қиылыспайтын эквивалентті кластарға бөлшектенеді.
Бұл кластар – m модулі бойынша қалындыла кластары деп аталады.
40.Модульдері бірдей екі немесе бірнеше салыстыруларды қосуға не азайтуға болады.
а1 ≡ b1 (mod m)
а2 ≡ b2 (mod m)
______________
a1 ± a2 ≡ b1 ± b2 (mod m)
a1 – b1 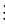 m
m
=> (a1 ± a2) - (b1 ± b2) =(a1 – b1) ± (a2 – b2) m a1 ± a2 ≡ b1 ± b2(mod m)
a2 – b2 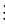 m
m
С алдарлар .
1. Салыстырудың кез келген мүшесін бір жағынан екінші жағына кері таңбамен көшіруге болады.
а + b ≡ с (mod m) => а ≡ с – b (mod m)
- b ≡ - b (mod m)
_______________
а ≡ с – b (mod m)
2. Салыстырудың екі жағына да модульге еселі санды қосуға не азайтуға болады.
а ≡ b (mod m) => а ≡ b – mk (… m)
0 ≡ mk (… m)
50 Бірдей модульді салыстыруларды мүшелеп көбейтуге болады.
а1 ≡ b1 (mod m)
а2 ≡ b2 (… m)
_________________
a1a2 ≡ b1b2 (… m)
a1a2 – b1b2 = a1a2 – b1b2 + a1b2 – b1b2 = a1 (a2 – b2) + b2 (a1 – b1) m
С алдарлар .
1) Салыстырудың екі жағын да бірдей бүтін санға көбейтуге болады.
a ≡ b (… m) => ac ≡ bc (mod m) => a – b =mg => ac – bc ≡ m (gc)
2) Салыстырудың екі жағын да бірдей дәрежеге шығаруға болады.
a ≡ b (mod m) => an ≡ bn (mod m)
60 Салыстырудың екі жағын да модульмен өзара жай сан болып табылатын олардың ортақ бөлгішіне бөлуге болады.
aс ≡ bс (mod m) Λ (c, m) = 1 => a ≡ b (mod m) => ac – bc m => c (a – b) m Λ (c, m) = 1 =>a – b m
70 Салыстырудың екі жағын да және модульды бірдей оң бүтін санға көбейтуге болады.
a ≡ b (mod m), r (mod m) Є Z => ak ≡ bk (mod mr)
a – b = mg => ak – bk = (mr)g k Є Z
80 Егер ak ≡ bk (mod mk) => a ≡ b (mod m) мұндағы r, m – кез келген натурал сандар.
90 a ≡ b (mod m) Λ m d => a ≡ b (mod m) => a – b m и m d => a – b d
100 a ≡ b (mod m) => a мен m-нің барлық ортақ бөлгіштер жиыны, b мен m-нің барлықортақ бөлгіштер жиынымен бірдей болады, (a, m) = (b, m).
110 a ≡ b (mod m1)
a ≡ b (mod m2)
-------------------
a ≡ b (mod mk) где m ≡ [m1, …, mk]
120 f(x) – бүтін коэффициентті көпмүшелік болсын, a ≡ b (mod m) =>
f(a) ≡ f(b) (mod m)
2 Қалындылардың толық және келтірілген жүйесі
3 анықтама . Берілген модуль бойынша әрбір қалындылар класынан бір-бірден таңдап алынған сандар жүйесін қалындылардың толық жүйесі деп аталады.
Мысалы: 6 модулі бойынша : 12,-13,2,63,-2,5
Әрбір клсастан бір-бірден қалындылар алып, берілген модуль бойынша шексіз көп қалындылардың толық жүйесін құруға болады.
Қалындылар жүйесі фигуралы жақшасыз жазылады.
a) Ең кіші теріс емес қалындылардың толық жүйесі 0,1, …. ,m-1
(мысалда 0,1,2,3,4,5)
б) Ең кіші абсолют қалындылардың толық жүйесі (абсолют шамасы бойынша ең кіші сандардан құралады)
Мысалда: 2,-1,0,1,2,3
Қасиеттері
1 теорема. M бүтін сандардың кез келген жиыны, қос-қостан m модулі бойынша салыстырымды емес, m модулі бойынша қалындылардың толық жүйесін құрайды.
2 теорема. Егер (a,m)= 1 және 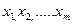 қалындыладың толық жүйесі болса, онда
қалындыладың толық жүйесі болса, онда 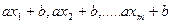 сандары да m модулі бойынша қалындыладың толық жүйесі болады.
сандары да m модулі бойынша қалындыладың толық жүйесі болады.
3 анықтама. Егер ( 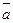 ,m ) = 1 боолса, онда m модулі бойынша
,m ) = 1 боолса, онда m модулі бойынша 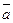 қалындылар класы m модулімен өзара жай болады.
қалындылар класы m модулімен өзара жай болады.
Кез келген модуль үшін өзара жай кластар табылады.
Мысалы: m=6 үшін өзара жай кластар 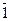 ,
, 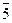 кластары болады.
кластары болады.
m=7үшін , 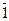 ,
, 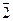 ,
, 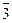 ,
, 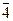 ,
, 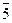 ,
, 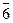 өзара жай кластар .
өзара жай кластар .
m модулі бойынша өзара жай кластар 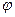 (m) деп белгіленеді және Эйлер функциясы деп аталады.
(m) деп белгіленеді және Эйлер функциясы деп аталады.
Эйлер функциясы m –н өзара жай m –н артық емес сандардың санын көрсетеді.
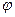 (6)=2 ;
(6)=2 ; 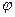 (7)=6
(7)=6
Егер модуль жай сан болса, яғни m= р, онда нөлдік кластан басқа барлық кластар m –н өзара жай болады.
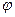 (p)=p-1 өзара жай кластар саны
(p)=p-1 өзара жай кластар саны
5 анықтама. m модулімен өзара жай болатын әрбір қалындылар класынан алынған қалындылар жиынтығы m модулі бойынша қалындылардың келтірілген жүйесі деп аталады.
3 Эйлер ф ункция сы . Эйлер және Ферма т еорем алар ы
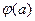 Эйлер функциясы барлық натурал сандар үшін анықталады және а - мен өзара жай 1,..,а-1 сандар қатарынан алынады.
Эйлер функциясы барлық натурал сандар үшін анықталады және а - мен өзара жай 1,..,а-1 сандар қатарынан алынады.
Теорема.
Егер 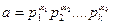 - а санының канондық түрдегі жіктелуі болса, онда
- а санының канондық түрдегі жіктелуі болса, онда
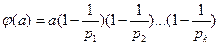
Т еорема.
р – жай сан болсын, 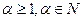 , онда
, онда 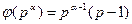
Эйлер және Ферма теоремалары барлық салыстыоулар теориясының негізі болып табылады, теориялық зерттеулерде де, арифметикалық қосымшаларда да кеңінен қолданылады.
Мысал. 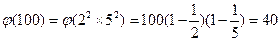
Эйлер теоремасы.
Егер (a,m)=1 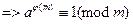 a
a 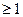 (I)
(I)
Эйлер теоремасын m=p – жай сан болған кезде қарастырамыз. Бұл жағдайда φ(p)=p-1, сондықтан келесі теорема шығады.
Ферма теоремасы . Егер р – жай сан болса және 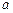 саны р –ға бөлінбейтін бүтін сан болса, онда
саны р –ға бөлінбейтін бүтін сан болса, онда
( 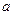 ,p)=1, то
,p)=1, то 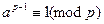 (II)
(II)
Ферма теоремасының басқаша айтылуы: (Салдар)
Егер р – жай сан болса, онда кез келген 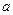 бүтін саны үшін келесі теңдік орын алады
бүтін саны үшін келесі теңдік орын алады 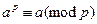
Расында да,
а) егер (а,р)=1 (II) салыстырудың екі жағын да 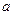 -ға көбейтіп,
-ға көбейтіп, 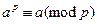 аламыз.
аламыз.
б) егер (а,р)≠1, онда 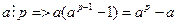 да р –ға бөлінеді, яғни
да р –ға бөлінеді, яғни 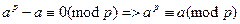
4 Бір белгісізі бар бірінші дәрежелі салыстырулар
Кез келген бір белгісізі бар бірінші дәрежелі салыстыруды келесі түрге келтіруге болады:
ах 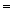 b (mod m) (I)
b (mod m) (I)
a 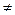 0 (mod m)
0 (mod m)
(I) салыстыруының жалғыз шешімі, бірнеше шешімі, мүлде шешімі болмауы мүмкін.
1 т еорема . Егер (a,m) = 1 болса, онда (1) салыстыруының шешімі бар және жалғыз болады.
2 т еорема . Егер (a,m)=d>1 және b d-ға бөлінбесе , онда (1) салыстыруының шешімі жоқ.
3 теорема. Егер (a,m)=d>1 және b 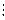 d, онда (1) салыстырудың d әртүрлі шешімі бар болады. Бұл шешімдердің барлығы
d, онда (1) салыстырудың d әртүрлі шешімі бар болады. Бұл шешімдердің барлығы 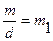 модулі бойынша бір класс құрайды.
модулі бойынша бір класс құрайды.
Әдебиет: 8, 22-29 бет, 16, 40-56 бет
Бақылау сұрақтары:
1. Қандай сандар модулі бойынша салстырымды деп аталады.
2. Эйлер функциясы қалай анықталады? Оны табу формуласы қандай.
3. Эйлер және Ферма теоремаларын айтыңыз.
4. Қалындылардың толық және келтірілген жүйесі дегеніміз не.
5. Бір белгісізі бар бірінші дәрежелі салыстырулар қалай шешіледі ?
8 та қ ырып
Диофант ты теңдеулер .
М ақсаты :
1. Тарихи шолу жасау.
2. Екі белгісізі бар бірінші дәрежелі анықталмаған теңдеулерді шешуді қарастыру.
3. Практикалық есептер шығаруда дағды мен біліктілікті қалыптастыру.
Жоспар :
1. Диофантты теңдеулер – тарихи шолу.
2. Диофантты теңдеулерді шешудің екі кезеңі.
1 Диофант ты теңдеулер – тарихи шолу
Диофант өмірі ғылым тарихында өте жұмбақ болып көрінеді. Диофант өмір сүрген аралық шамамен 500 жыл аралығын қамтиды, ал дәл өмір сүрген уақыты белгісіз. Диофант 3 ғасырда ғылым орталығы деп есетелетін Александрия қаласында тұрған. Ол анықталмаған теңдеулерді рационал сандарда шешу мәселесін және оларды шешу әдістерін қарастырған.
Оның әдістері түсінікті болған және Виет пен Ферманың жаңа есептерінде қолданыс тапқан.
Анықталмаған теңдеулерді бүтін сандарда шешу мәселесімен Эйлер, Лагранж және Лежандр айналысқан.
Анықталмаған теңдеулерді шешу есептерін қарастыратын математика бөлімі – диофантты талдау (жиі диофантты геометрия) деген атау алған.
1 анықтама. Екі белгісізі бар бірінші дәрежелі анықталмаған теңдеу деп ах +bу=с (1) теңдеуі аталады, мұндағы a,b,c 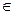 Z, a
Z, a 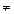 0, b
0, b 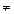 0.
0.
Бірнеше белгісізі бар теңдеулердің шексіз көп шешімі бар, сондықтан мұндай теңдеулер анықталмаған теңдеулер деп аталады.
Егер с ≠ 0 болса, онда (1) теңдеуі біртекті емес теңдеу деп аталады (немесе оң жағы бар теңдеу). Ал егер с=0 болса, яғни ах +bу=0 (2) теңдеуі берілген (1) теңдеуіне сәйкес біртекті теңдеу деп аталады.
(1) теңдеуінің бүтін сандарда шешілуін қарастырамыз.
2 анықтама. (1) анықталмаған теңдеудің бүтін сандардағы шешімі деп, осы теңдеуді қанағаттандыратын (х0,у0) бүтін сандар қосы аталады.
(яғни, (1) теңдеуіндегі белгісіздер орнына қойғаннан ах0+bу0=с сандық теңдік шықса).
(х0,у0) жеке шешімдер (1) теңдеуінің дербес шешімдері деп аталады; жалпы шешңм мүмкін болатын дербес шешімдерден тұрады (барлық дербес шешімдер жиынтығы).
Теорема 1. (1) бүтін коэффициентті екі белгісізі бар бірінші дәрежелі анықталмаған теңдеудің (а,b)=d болып, оң жағы с коффициенті d –ға бөлінбесе, онда (1) теңдеуінің шешімі болмайды.
(а,b)  =d
=d  >1
>1 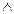
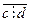
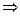 шешімі болмайды.
шешімі болмайды.
2 Диофант ты теңдеулерді шешудің екі кезеңі
Бүтін шешімді табу кеі кезеңге бөлінеді:
I. (1) теңдеуінің шешімі бар екенін дәлелдеу және осы шешімді табу әдісін көрсету.
II. Жалпы шешімді табу.
I кезең . Дербес шешімді табу.
Бүтін шешімді іздеу салыстыруларды шешумен тығыз байланысты.
2 т еорема . Егер (х0, у0) –(1) теңдеуінің бүтін шешімі болса, мұндағы а 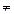 0, b
0, b 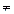 0, онда х0 -
0, онда х0 - 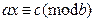 теңдеуінің шешімі болады.
теңдеуінің шешімі болады.
Керісінше , егер х0 – 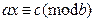 (4) салыстырудың шешімі болса, онда (х0, у0) - (1) анықталмаған теңдеудің шешімі болатындай,
(4) салыстырудың шешімі болса, онда (х0, у0) - (1) анықталмаған теңдеудің шешімі болатындай, 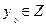 табылады.
табылады.
Дәлелдеуі: 1) (х0, у0) – ах+bу=с теңдеуінің бүтін шешімдерінің бірі болсын 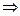 ах
ах 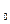 - с= -by0
- с= -by0 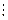 b
b 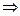 ax0
ax0 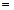 c(mod b)
c(mod b) 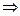 x0 – (4) салыстырудың шешімі.
x0 – (4) салыстырудың шешімі.
2) х0 – (4) салыстырудың шешімі болсын 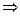
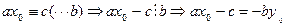 , мұндағы у0
, мұндағы у0 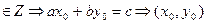 - ах+bу=с анықталмаған теңдеудің бүтін шешімі.
- ах+bу=с анықталмаған теңдеудің бүтін шешімі.
1 салдар :
Егер (а,b)=d болса және с коэффициенті d-ға бөлінсе, онда ах+bу=с анықталмаған теңдеудің бүтін шешімі бар болады.
Дербес шешімді ЕҮОБ сызықты түрде өрнектеу арқылы шешу:
ах+bу=1 теңдеуін қарастырамыз.
х0, у0 – оның шешімі болсын. Егер (а,b)=1 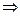 ах+bу=1 орындалатындай,
ах+bу=1 орындалатындай, 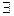
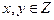 табылады. Ендеше (*) анықталмаған теңдеудің дербес шешімі
табылады. Ендеше (*) анықталмаған теңдеудің дербес шешімі
(х0с, у0с) түрінде болады.
II кезең: жалпы шешімді табу.
3 теорема. Егер бүтін коэффициентті анықталмаған теңдеудің бүтін дербес шешімі (х0, у0) болса, мұндағы (а, b)=1, онда осы теңдеудің жалпы шешімі келесі түрде болады:
(**) { 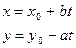
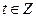
Әдебиет : 8, 38-42 бет
Өзін-өзі тексеруге арналған сұрақтар :
1. Екі белгісізі бар бірінші дәрежелі анықталмаған теңдеудің анықтамасын беріңіз.
2. Қандай диофантты теңдеулер біртекті және біртекті емес деп аталады?
3. Анықталмаған теңдеудің дербес шешімі дегеніміз не?
4. Диофантты теңдеулерді шешудің екі кезеңін көрсетіңіз.
9 тақырып
Пікірлер алгебрасы
Мақсаты :
1. Математикалық логика тарихына қысқаша шолу.
2. Математикалық логиканың негізгі түсініктеріне кіріспе.
3. Практикалық есептер шығаруда біліктілік пен дағдыны қалыптастыру.
Жоспар :
1. Пікір. Мысалдар.
2. Пікірлерге қолданылатын амалдар.
3. Пікірлер алгебрасының функциясының кесте арқылы берілуі.
Кіріспе
"Логика" термині гректің logoz (логос) деген сөзінен шыққан. Бұл сөздің мағынасы "түсінік", "ес, ақыл-ой" дегенді білдіреді. Логика ғылым ретінде ойлауды оқытады.
Логика едұрыс ойлаудың формалары мен заңдары туралы ғылым.
Математикалық логика дәстүрлі локикадан дамыған. Бұл ғылым дұрыс ойлаудың жалпы құрылымын зерттеу үшін математикалық әдістерді қолданып, математиканың бір бөлімі болып қалыптасты. Логиканың ғылым ретінде негізін салған ежелгі грек философы және ғалымы Аристотель (384 - 322 ж. б.э.д.) болатын. Ол дедукция теориясын, яғни логикалық түрде қорыту теориясын жасап шығарды.
1 Пікір. Мысалдар.
Пікірлер алгебрасы бар пікірлерден пікір құру әдістерін, заңдылықтарын оқытады. Пікірлер алгебрасы математикалық логиканың негізі болып табылады.
Анықтама 1. Пікір деп, мағынасы бойынша немесе ақиқат, немесе жалған болып табылатын хабарлы сөйлемді айтады.
Пікір бір мезгілде ақиқат және жалған болуы мүмкін емес.
Мысалы: 1) “2+5=1” - ж
2) “14:3” - пікір емес
Кез-келген сөйлем пікір болып табылмайды. Мысалы, сұраулы және лепті сөйлемдер пікір болмайды. Анықтама да пікр емес.
Ақиқат пікірге – 1 символын, ал жалған пікірге – 0 символын сәйкестендіреміз.
Барлық пікірлер жиынында 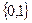 екі элементті жиыннан мәндер қабылдайтын
екі элементті жиыннан мәндер қабылдайтын 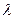 ақиқаттық функция анықталады:
ақиқаттық функция анықталады:
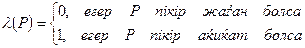
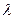 функциясы ақиқаттық функция деп, ал оның
функциясы ақиқаттық функция деп, ал оның 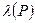 мәні Р пікірінің ақиқаттық мәні деп аталады
мәні Р пікірінің ақиқаттық мәні деп аталады
Қарапайым (элементар) пікірлерге амалдар қолдану арқылы күрделі пікірлер алуға болады.
Логикалық амалдар
2 анықтама. А және В екі пікірдің конъюнкциясы деп, А^В деп белгіленетін(А және В деп оқылады), берілген A және B екі пікір де ақиқат болғанда ақиқат болатын, ал қалған жағдайлардың бәрінде де жалған болатын жаңа пікірді атайды.
| А | В | А^В |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Ақиқаттық кесте:
Мысал:
1) «8 саны 2-ге бөлінеді және 4-ке бөлінеді». Пікірдің мәні ақиқат.
2) «12 саны жұп сан және жай сан». Пікірдің мәні жалған.
3)
3 анықтама. Екі пікірдің д изъюнкци ясы деп, АvВ деп белгіленетін (А немесе В деп оқылатын), берілген екі пікірдің кемінде біреуі ақиқат болғанда ақиқат, ал А және В екі пікір де жалған болғанда, жалған болатын жаңа пікірді айтады.
| А | В | АvВ |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Ақиқаттық кесте:
Мысалы: «7 кіші 4-тен немесе 42 саны 7- ге бөлінеді».
Пікірдің мәні ақиқат.
4 анықтама. Екі пікірдің импликациясы деп, А→В деп белгіленетін(егер А, онда В деп оқылатын), егер А ақиқат, ал В- жалған болса жалған, ал қалған уақытта ақиқат болатын жаңа пікірді атайды.
| А | В | А→В |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Ақиқаттық кесте:
А→В пікірінде А - алғы шарт немесе анцедент, ал В пікірі – салдар, нәтиже немесе консеквент деп аталады.
Мысалы: «Егер 48 саны 8-ге бөлінсе , онда ол 4-ке еселі». А 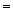 1; В
1; В 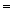 1
1 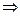 A→B
A→B 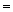 1.
1.
5 анықтама. Екі пікірдің э квивалент тігі деп, А↔В деп белгіленетін (А содн тек қана сонда, қашан В деп оқылатын), егер берілген А және В пікілерінің екеуі де жалған болған кезде ақиқат, ал қалған жағдайларда жалған болатын жаңа пікірді атайды.
Ақиқаттық кесте:
| А | В | А↔В |
| А | А | А |
| А | Ж | Ж |
| Ж | А | А |
| Ж | Ж | А |
Мысал: «Сан 3-ке бөлінеді сонда тек сонда ғана, егер оның цифрларының қосындысы 3-ке бөлінсе »
Бұл теоремада екі импликация бар:
1) А→В (шарт пен қорытынды орындарымен ауысқан)
2) В→А
3)
6 анықтама. А пікірінің терістеуі деп, 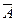 деп белгіленетін және берілген А пікірі жалған болса, ақиқат мән қабылдайтын, керісінше А пікірі ақиқат болса, жалған болатын жаңа пікірді атайды.
деп белгіленетін және берілген А пікірі жалған болса, ақиқат мән қабылдайтын, керісінше А пікірі ақиқат болса, жалған болатын жаңа пікірді атайды.
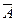 деп белгіленеді, « А емес » деп оқылады.
деп белгіленеді, « А емес » деп оқылады.
Мысал ”2<3”.
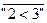 - бұл пікірдің терістеуі “2 саны 3-тен кіші емес”.
- бұл пікірдің терістеуі “2 саны 3-тен кіші емес”.
| А | 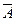
|
| 1 | 0 |
| 0 | 1 |
Ақиқаттық кесте:
Әдебиет : 1, 101-103 бет, 3, 5-57 бет, 5,13 бет, 6, 10-15 бет
Бақылыу сұрақтары :
1. Пікір дегеніміз не? Пікірдің мысалдарын келтіріңіз.
2. Қандай логикалық амалдар бар? Қандай ақиқаттық кестелер арқылы анықталады?
3. Логикалық амалдар барлық жағдайларда бір-бірімен мағынасы бойынша байланысады ма?
4. Берілген логикалық амалдардың қайсысы бинарлық болады?
10 тақырып
Формул алар . Формулалардың мәндестігі .
Формулалардың классификациясы .
Мақсаты :
1. Пікірлер алгебрасының формулалары түсінігін енгізу.
2. Буль алгебрасының негізгі заңдарын оқыту.
3. Логикалық формулалардың классификациясын қарастыру.
4. Практикалық есептерді шығаруда дағды мен біліктілікті қалыптастыру.
Жоспар :
1. Пікірлер алгебрасының формулалары, олардың мәндестігі.
2. Негізгі мәндестік формулалар (буль алгебрасының заңдары)
3. Логикалық формулалардың классификациясы.
1 Пікірлер алгебрасының формулалары , олардың мәндестігі
Қарастырылған логикалық амалдардың ( 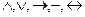 ) көмегі арқылы жай пікірлерден күрделі пікірлер құруға болады.
) көмегі арқылы жай пікірлерден күрделі пікірлер құруға болады.
1 анықтама. Орындарына нақты пікірлерді қоюға болатын айнымалылар пропозицианалды айнымалылар немесе айнымалы пікірлер деп аталады.
Бұл айнымалылар үлкен латын әріптерімен белгіленеді.
2 анықтама. Пікірлер алгебрасының формулалары келесі түрде анықталады:
а) Әрбір пропозиционалдық айнымалы формула болып табылады
б) Егер 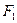 және
және 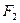 - формулалар болса, онда
- формулалар болса, онда
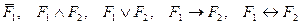 де формулалар болады
де формулалар болады
в) Алдыңғы екі ереже бойынша құрылған формулалардан басқа
фомулалар жоқ.
Бұл анықтама индуктивті анықтама деп аталады.
3 анықтама . Егер пікірлер алгебрасының 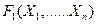 және
және 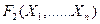 фомулаларының құрамына кіретін пропозиционалды айнымылылардың кез келген мәнінде F1 және F2 формулаларының мәндері бірдей болса, онда бұл формулалар мәндес деп аталады.
фомулаларының құрамына кіретін пропозиционалды айнымылылардың кез келген мәнінде F1 және F2 формулаларының мәндері бірдей болса, онда бұл формулалар мәндес деп аталады.
Белгіленуі: F1≡ F2, F1<=> F2
Кез келген күрделі пікір (формула) аргументтері 0 немесе 1 мәнін қабылдайтын (бір-біріне тәуелсіз) фнкцияны анықтайды, ал функцияның өзінің мәні {1, 0} жиынына тиісті болады. Мұндай функциялар буль функциялары деп аталады.
Мысал. 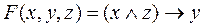
2 Негізгі мәндестік формулалар (буль алгебрасының заңдары)
A, B, C – буль функциялары болсын.
Теорема: A, B, C – буль функциялары үшін келесі мәндестіктер тура болады:
1. Коммутативті: 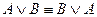 ;
; 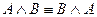
2. Ассоциативті: 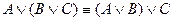 ;
; 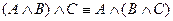
3. Дистрибутивті: 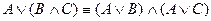 ;
; 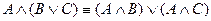
4. Де Морган заңдары: 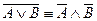 ;
; 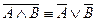
5. Екі рет терістеу заңы (инволюция): 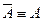
6. Жұтып қою заңы: 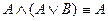 ;
; 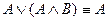
7. Идемпотентті заңы: 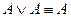 ;
; 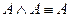
8. Үшіншіні жоққа шығару заңы: 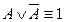 ;
;
9. Қарама- қайшылық заңы: 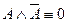 ;
;
10. 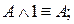
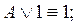
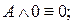
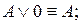
11. 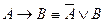
12. 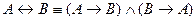
Негізгі мәндестіктер арқылы берлген формуланы түрлендіріп, ықшамдауға болады.
Формулаларды ықшамдаған кезде 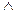 (яғни логикалық көбейту) ең күшті операция болып есептеледі, одан кейін
(яғни логикалық көбейту) ең күшті операция болып есептеледі, одан кейін 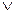 (яғни, логикалық қосынды) болады, ал
(яғни, логикалық қосынды) болады, ал 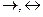 келесі ретте орындалады.
келесі ретте орындалады.
3 Логикалық формулалардың классификациясы
Логикалық формлалардың келесі классификациясын қарастырамыз: ақиқат формулалар немесе тавталогиялар, жалған формулалар немесе қарама-қайшы, орындалатын формулалар.
4 анықтама . Егер формуланың құрамына енетін айнымалы пікірлердің барлық мәндерінде формула ақиқат мән қабылдаса, онда берілген формула ақиқат немесе тавталогия деп аталады.
Мысал: 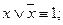
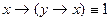
5 анықтама . Егер формуланың құрамына енетін айнымалы пікірлердің барлық мәндерінде формула жалған мән қабылдаса, онда берілген формула жалған немесе қарама-қайшы деп аталады.
Мысал: 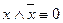
6 анықтама . Егер формуланың құрамына енетін айнымалы пікірлердің кейбір мәндерінде формула ақиқат немесе жалған мән қабылдаса, онда берілген формула орындалатын деп аталады.
Мысал: 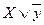 ;
; 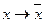
F формуласының мәні келесі түрде белгіленеді: I(F)
1 т еорема: F - қандай-да бір формула болсын.
Онда 1. егер F-тавтология болса, онда 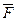 -қарама-қайшылық.
-қарама-қайшылық.
2. егер F- қарама-қайшы болса, онда 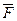 - тавтология.
- тавтология.
Дәлелдеуі : тікелей анықтамадан шығады.
2 т еорема : Егер F және F 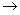 Q формулалары тавтологиялар болса, онда
Q формулалары тавтологиялар болса, онда
Qформуласы да - тавтология.
Дәлелдеуі :кері жорудан шығады.
I(Q) 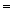 0 болсын, I(Q)
0 болсын, I(Q) 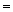 1 ( шарт бойынша .)
1 ( шарт бойынша .) 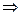 I(F
I(F 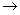 Q)=0, бұл
Q)=0, бұл
F 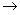 Q - тавтология дегенге қайшы.
Q - тавтология дегенге қайшы.
Қорытынды:
Логикалық байланыстарды қарастырған кезде ,біз оның мазмұнына емес, тек қана логикалық мәніне назар аударамыз. Сондықтан кез келген пікірді {0,1} екі элементті жиында анықталған қандай да бір амалдар ретінде қарастыруға болады.
0^0=0 0^1=1^0=0 1^1=1
Әдебиет: 1, 101 бет, 5, 31 бет, 6, 16-23 бет;
Бақылыу сұрақтары:
1. Пікірлер алгебрасының формулалары дегеніміз не?
2. Пікірлер алгебрасының қандай формулалары мәндес деп аталады?
3. Буль алгебрасының заңдары атап шығыңыз.
4. Логикалық формулалардың негізгі заңдарының анықтамаларын айтыңыз. Мысалдар келтіріңіз.
5. Логикалық формулалардың негізгі түрлері арасында қандай байланыс бар.
11 тақырып
П і к і рлер алгебрасыны ң тавталогиялары .
Нормаланған формалар.
Мақсаты :
1. Шешілімдік мәселесі мен екіжақты заңды қарастыру.
2. Тавталогия түсінігін және оны алу ережесін енгізу.
3. ДНФ, КНФ, жетілдірілген ДНФ, жетілдірілген КНФ түсініктерін енгізу.
4. Пікірлер алгебрасы үшін нормаланған формалар мен жетілдірілген ДНФ
және КНФ анықтауда біліктілік пен дағдыны қалыптастыру.
5. Пікірлер алгебрасының тавталогияларын анықтауда біліктілік пен
дағдыны қалыптастыру.
Жоспар :
1. Екіжақтылық заңы.
2. Шешілімділік мәселесі.
3. Негізгі тавталогиялар. Тавталогияларды алу ережесі.
4. Нормаланған формалар: ДНФ, КНФ.
5. Жетілдірілген нормаланған формалар: ДНФ, КНФ.
Екіжақтылық заңы
Құрамында тек қана конъюнкция, дизъюнкция және терістеу амалдары бар формулаларды қарастырамыз ( кез келген формула мәндес түрлендірулер арқылы осы түрге келтіріледі).
Анықтама . Конъюнкция ( 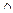 )операциясы дизъюнкция (
)операциясы дизъюнкция ( 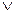 ) операциясына қатысты екіжақты деп аталады.
) операциясына қатысты екіжақты деп аталады.
Анықтама. F және F* формулалары бір-бірінен әрбір операцияны екіжақты операцияға алмастырғаннан шықса, онда олар екіжақты формулалар деп аталады.
Мысал: F=(X 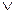
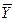 )
) 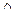 Z; F* =(X
Z; F* =(X 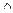
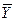 )
) 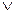 Z.
Z.
Мәндестік формулалардан (Де Морган заңдарынан ) келесі тұжырым оңай шығады:
(1) 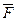 (X1,…,Xn)
(X1,…,Xn) 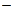 F*(
F*( 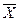 1,…,
1,…, 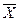 n).
n).
Осы қатынастан екіжақтылық заң шығады:
Екіжақтылық заңы:
Егер F және F1 формулалары мәндес болса, онда оларға екіжақты F* және F*1 формулалары да мәндес болады.
(2) F 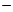 F1
F1 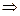 F*
F* 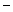 F*1 F*(X1,…,Xn)
F*1 F*(X1,…,Xn) 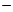
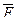 *(
*( 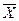 1,…,
1,…, 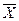 n).
n).
Мысал: F=A 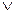 B
B 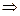 F* =A
F* =A 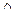 B
B 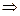
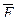 (
( 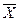 1,…,
1,…, 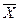 n)=
n)= 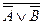
A 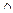 B
B 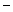
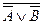
F 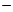 F1
F1 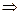 F(
F( 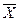 1,…,
1,…, 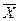 n )
n ) 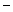 F1(
F1( 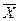 1,…,
1,…, 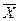 n )
n )
 (1)
(1)
X 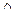 (Y
(Y 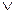 Z)
Z) 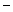 (X
(X 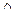 Y)
Y) 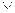 (X
(X 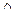 Z)
Z)
(2)
X 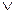 (Y
(Y 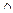 Z)
Z) 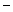 (X
(X 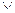 Y)
Y) 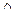 (X
(X 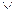 Z)
Z)
Егер F формуласына (1) дистрибутивті заңды қолдану арқылы F1 формуласын алсақ, онда F*екіжақты формуладан F* 1 екіжақты формулаға өту де (2) дистрибутивті заң арқылы жүзеге асады (дистрибутивті түрлендірулер).
F* формуласынан F* 1 формуласына өтетін түрлендірулер, F формуласынан F1 формуласына өтетін түрлендірулерге екіжақты деп аталады.
F 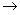 F1
F1 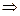 F*
F* 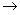 F* 1
F* 1
Тавтологиялар
Тавтологиялар оны құрайтын пікірлердің мазмұнына және ақиқат немесе жалған екеніне тәуелсіз, ақиқат пікірлерді құру үлгісін көрсетеді. Тавталогиялардың негізгі мәні: олардың кейбіреуі дұрыс ой-тұжырымдар жасауға мүмкіндік береді. Ақиқат алғышарттар әрдайым ақиқат қорытындыға келеді.
Теорема. Келесі пікірлер алгебрасының фрмулалары тавталогиялар болып табылады:
 1.1. Үшіншіні жоққа шығару заңы
1.1. Үшіншіні жоққа шығару заңы
|= Х V Х
1.2. Қарама-қайшылықты терістеу заңы
 |= Х Λ Х
|= Х Λ Х
1.3. Екі рет терістеу заңы 

Х « Х
1.4. Теңбе-тең заңы
Х → Х

 1.5. Контрапозиция заңы
1.5. Контрапозиция заңы
(Х → У) « (У → Х)
1.6. Силлогизм заңы
((Х →У) Λ (У → Z)) → (Х → Z)
1.7. Қарама-қарсылық заңы
(Х « У) « (Х « У)
1.8. Антецедентті қосу заңы («истина из чего угодно»)
Х → (У → Х)
 1.9. «из ложного что угодно» ережесі
1.9. «из ложного что угодно» ережесі
Х → (Х → У)
1.10. «modus ponens» ережесі
(X Λ (Х → У)) → У

 1.11 «modus tollens» ережесі
1.11 «modus tollens» ережесі
((Х → У) Λ У) → Х
1.12. Алғышарттарды орынауыстыру ережесі
(Х → (У → Z)) « (У → (Х → Z))
1.13. Алғышарттарды біріктіру (және айыру) ережесі
(Х → (У → Z)) « ((Х Λ У) → Z)
1.14. Оқиғаларды сараптау ережесі
((Х → Z) Λ (У → Z) « ((Х V У) → Z


 1.15. Жоққа келтіру ережесі
1.15. Жоққа келтіру ережесі

 ((Х → У) Λ (Х → У) → Х
((Х → У) Λ (Х → У) → Х
(Х → (У Λ У)) → Х
Келесі тавталогиялар логикалық амалдардың қасиеттерін көрсетеді.
I. К онъюнкци я мен дизъюнкци яның қасиеттері .
2.1. Идемпотентті заңы
|= Р Λ Р « Р, Р V Р « Р
2.2. Қысқарту заңы
|= (Р Λ Q) → Р; Р → (Р → Q)
2.3. Коммутативті заңдар
|= Р Λ Q « Q Λ Р; Р V Q « Q V Р
2.4. Ассоциативті заңдар:
|= (Р V Q) V R « Р V (Q V R);
2.5. Дистрибутивті заңдар:
Р Λ (Q V Р) « (Р Λ Q) V (Р Λ R)
Р V (Q Λ Р) « (Р V Q) Λ (Р V R)
2.6. Жұтып қою заңдары:
Р Λ (Р V Q) « Р; Р V (Р Λ Q) « Р
2.7. Де Морган заңдары:





 |= Р Λ Q « Р V Q; Р V Q « Р Λ Q
|= Р Λ Q « Р V Q; Р V Q « Р Λ Q
Им пликаци я мен эквивален цияның қасиеттері
3.1. (Р → (Q → Р)) → ((Р → Q) → (Р → R))
3.2. Р → (Q → (Р Λ Q))
 3.3. (Р → R) → ((Q → R) → ((Р V Q) → R))
3.3. (Р → R) → ((Q → R) → ((Р V Q) → R))

 3.4. (Р → Q) → ((Р → Q) → R
3.4. (Р → Q) → ((Р → Q) → R
3.5. (Q Λ (Р → Q)) → Р
 3.6. (Р Λ (Р V Q)) → Q
3.6. (Р Λ (Р V Q)) → Q
3.7. (Р → Q) → ((Р V R) → (Q V R))
3.8. (Р → Q) → ((Р Λ R) → (Q Λ R))
3.9. (Р → Q) → ((Q → R) → (Р → R))

 3.10. (Р → Q) V (Q → Р)
3.10. (Р → Q) V (Q → Р)
3.11. (Q → Р) → ((Q → Р) → Q)
3.12. ((Р → Q) Λ (R → Q)) « ((Р V R) → Q
3.13. (((Р → Q) Λ (Р → R)) « (Р → (Q Λ R))
3.14. Р « Р
3.15. (Р « Q) « (Q « Р)
3.16. ((Р « Q) Λ (Q « R)) → (Р « R)
Тавталогия алудың негізгі ережелері
Жаңа тавталогиялар алу ережелерін қарастырамыз
1 т еорема. (қорытынды ережесі) «modus ponens» ережесі
Егер F және F → Н формулалары тавталогиялар болса, онда Н формуласы да тавталогия.
Басқаша айтқанда |= F және |= F → Н болса, онда |= Н.
Теорема 2. (орнына қою ережесі)
Егер құрамында Х пропозиционалды айнымалысы бар F формуласы тавталогия болса, онда F формуласындағы Х айнымалының орнына кез келген Н формуласын қойғаннан тавталогия аламыз.
Басқаша айтқанда: егер |= Fболса, онда |= 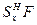
Мысал:
|= Х → (У → Х)
(х1 Λ х2) формуласын Х орнына қоямыз,
|= (х1 Λ х1) → (У → (х1 Λ х2)) нәтижесінде тавталогия аламыз.
Шешілімділік мәселесі
Біз берілген формула ақиқат па, жалған ба, әлде орындалатын екенін анықтайтын тәсілдерді қарастырдық, ендеше осы сұрақты 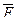 формуласы үшін де шешуге болады.
формуласы үшін де шешуге болады.
Егер 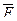 ақиқат формула болса, онда F – жалған формула болады (орындалмайтын).
ақиқат формула болса, онда F – жалған формула болады (орындалмайтын).
Егер 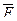 ақиқат формула болмаса, онда F- жалған формула болмайды, яғни орындалатын формула болады.
ақиқат формула болмаса, онда F- жалған формула болмайды, яғни орындалатын формула болады.
Қойылған мәселе «шешілімділік мәселесі» деп аталады.
(Ол тек қана пікірлер алгебрасы үшін ғана емес, басқа да логикалық жүйелер үшін де қойылады).
Пікірлер алгебрасы үшін бұл мәселе оңай шешіледі.
1. F(X1,…,Xn ) – құрамында X1,…,Xn элементар пікірлер бар, пікірлер алгебрасының формуласы болсын.
Бұл формула екі мән қабылдай алатын X1,…,Xn айнымалыларға қатысты қандай-да бір функцияны анықтайды.
X1,…,Xn айнымалыларының мәндерінің мүмкін болатын комбинацияларының саны 2n тең. Кез келген комбинация үшін айнымалылардың мәні кесте арқылы анықталады.
Аталған тәсіл шешілімділік мәселесінің шешуі болып табылады, бірақ өте көп сынау жүргізу керек.
2. Берілген формуланы «нормаланған түрге» келтіру деп аталатын, екінші тәсіл де бар.
Анықтама . Айнымалылардың және олардың терістеулерінің көбейтіндісі (қосындысы) элементар көбейтінді ( 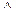 ) (сәйкесінше элементар қосынды (
) (сәйкесінше элементар қосынды ( 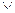 )) деп аталады.
)) деп аталады.
X 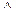
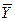
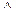 Z X
Z X 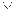
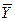
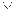 Z
Z
Элементар көбейтінді элементар қосынды
1 теорема . Элементар қосынды ақиқат болу үшін, оның құрамындағы қосындылардың кем дегенде бір қосында айнымалының өзі және оның терістеуінің болуы қажетті және жеткілікті.
Y 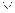 Z
Z 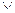 X
X 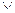
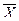
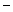 1 , мұндағы X
1 , мұндағы X 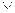
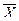
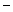 1.
1.
2 теорема. Элементар көбейтінді жалған болу үшін, оның құрамындағы көбейткіштердің кем дегенде бір бір қосында айнымалының өзі және оның терістеуінің болуы қажетті және жеткілікті.
Y 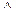 Z
Z 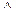 X
X 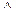
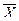
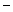 0 , мұндағы X
0 , мұндағы X 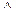
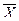
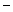 0.
0.
Пікірлер алгебрасының формулалары үшін нормаланған формалар
Пікірлер алгебрасының әрбір формуласы үшін, тек қана терістеу, конъюнкция мен дизъюнкция арқылы байланысқан мәндес формуланы көрсетуге болады ( ол үшін 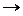 ,
, 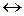 амалдары
амалдары 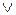 ,
, 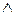 арқылы өрнектеледі). Берілген флормуланы
арқылы өрнектеледі). Берілген флормуланы  ,
, 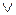 ,
, 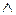 арқылы бірнеше тәсілмен өрнектеуге болады.
арқылы бірнеше тәсілмен өрнектеуге болады.
Мысал: 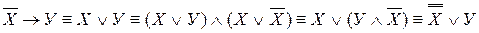

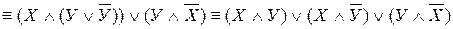
Анықтама . Х1 ,…,Хn айнымалылардың конъюнктивті бірмүшесі деп осы айнымалылардың конъюнкциясы немесе терістеуі аталады.
Мысал: 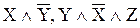 - элементар көбейтінді.
- элементар көбейтінді.
Анықтама . Х1 ,…,Хn айнымалылардың дизъюнктивті бірмүшесі деп осы айнымалылардың дизъюнкция сы немесе терістеуі аталады.
Мысал: 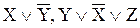 - элементар қосынды.
- элементар қосынды.
Анықтама. Конъюнктивті нормаланған форма (КНФ) деп дизъюнктивті бірмүшелердің конъюнкциясы аталады (немесе элементар қосындылардың көбейтіндісі )
Мысал: 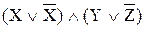
Анықтама . Дизъюнктивті нормаланған форма (ДНФ) деп конъюнктивті бірмүшелердің дизъюнкциясы аталады (немесе элементар көбейтінділердің қосындысы)
Мысал: 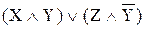
Әрбір формула үшін әрқашан да дизъюнктивті нормаланған форма да, конъюнктивті нормаланған форма да табылады. Де Морган және дистрибутивті қасиеттерді қолданып, бір формадан екінші формаға өтуге болады. Берілген F формуласы үшін шексіз көп дизъюнктивті, конъюнктивті нормаланған формалар табылады.
Мысал: КНФ және ДНФ табу керек:
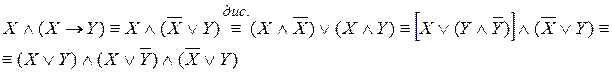
және т.б.
Көптеген ДНФ және КНФ арасында (берілген формула үшін) жалғыз келесі түрдегі форма табылады: жетілдірілген ДНФ және КНФ.
Анықтама . Х1,…,Хn айнымалыларына қатысты (конъюнктивті немесе дизъюнктивті) бірмүше жетілдірілген деп аталады, егер оның құрамына немесе айнымалының өзі кіретін болса, немесе оның терістеуі кіретін болса.
Анықтама . (Дизъюнктивті немесе конъюнктивті ) нормаланған форма жетілдірілген деп аталады, егер оның құрамына тек қана жетілдірілген бірмүшелер кіретін болса.
Мысал: Х1,Х2 айнымалыларына қатысты жетілдірілген КНФ табу керек:
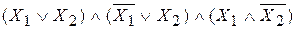
Әдебиет : 1, 86-90 бет; 6, 24-30 бет
Бақылау сұрақтары :
1. Қандай амалдар екіжақты деп аталады?
2. Қандай екі формула екіжақты деп аталады?
3. Тавталогия дегеніміз не?
4. Қандай негізгі тавталогияларды білесіз?
5. Тавталогия алудың негізгі ережелерін атаңыз.
6. Шешілімдік мәселесі дегеніміз не?
7. Элементар көбейтінді, элементар қосынды деп нені атайды?
8. Дизъюнктивті және конъюнктивті бірмүше дегеніміз не?
9. Дизъюнктивті және конъюнктивті нормаланған бірмүше дегеніміз не?
10. Жетілдірілген бірмүше қалай анықталады?
11. Қандай нормаланған форма жетілдірілген деп аталады?
12 тақырып
Теорияны аксиоматикалы қ т ү рде құ ру
Мақсаты :
1. Аксиоматикалық теория түсінігін енгізу.
2. Аксиома түсінігн және қорыту ережелерін енгізу.
3. Пеано аксиоматикасын қарастыру.
4.Толық математикалық индукция әдісімен дәлелдеуде дағды мен біліктілікті қалыптастыру.
Жоспар :
1. Аксиоматизация процесі.
2. Аксиомалар және қорыту ережелері.
3. Пеано арифметикасын аксиоматикалық түрде құру.
4. Толық математикалық индукция әдісі.
Қандай да бір мазмұнды теорияны формалды түрде көрсету оның жалпы қасиеттерін, пайдалы аналогтарын және жалпы сұрақтарға жауап беруге мүмкіндік береді. Дұрыс ойлау процесін формалды түрде көрсету аксиоматика түрінде жүзеге асады.
Формалды аксиоматикалық Т теория(синонимдер: формалды жүйе, есептеу) келесі түрде беріледі:
(1) Теорияның символдары деп аталатын, қандай да бір А символ д а р алфавиті. А алфавиттегі сөздер Т теорияда орнектер деп аталады.
(2) Т теорияның формула лары деп аталатын, өрнектердің қандай да бір ішкі жиынын айыру.
(3) Т теорияның аксиома лар деп аталатын, қандай да бір формулалар жиынын айыру.
Мазмұнды деңгейде – аксиомалар анықтама бойынша ақиқат формулалар.
(4) Әрқайсысы формулалар арасындағы қатынас болып есептелетін, R1,..., Rm қорытындылау ережелерінің ақырлы жиыны табылады.
Егер А1,…,Аk, В – формулалар және Ri(А1,…,Аk,В) қатынасы орындалса, онда В Ri ережесі бойынша алынған А1,…,Аk формулаларының тікелей салдары деп аталады.
Қандай да бір қорыту ережесін бір рет қолдану дұрыс ойлаудың, қарапайым қадамын көрсетеді.
Т теориясындағы қорытынды деп В1,В2,…,Вn формулаларының кез-келген тізбегі (шынжыр немесе кортеж аталады) Вi формуласы i=1,2,…,n, Т теориясындағы немесе аксиома, немесе осы тізбектің алдындағы қандай да бір формулалардың тікелей салдары болып табылады.
Қорытынды деп дәлелдеу барысында қарапайым қадамдарды тізбектеп қолдануды айтады.
Т теориясының С формуласы теорем а деп аталады, егер соңғы формуласы С болып табылатын қорытынды бар болатын болса. Бұл қорыту С формуласының қорытындысы деп аталады (ол Т теориясында жалғыз емес). С формуласын қорытудағы аксиомалардан басқа барлық формулалар да осы теорияның теоремалары болады. Сонымен аксиоматикалық теориядағы теоремелар – қабылданған ережелер бойынша аксиомалардан қорытылып шығарылатын формулалар.
Жалпы мағынада, қорытындыны тек қана аксиомалардан ғана емес деп қарастыруға болады. Г ={B1,…,Bn} формулалар жиыны үшін А1,..., Аm формулалар тізбегі бар болсын, кез -келген i=1,…,m үшін Аi формуласы – немесе теорияның аксиомасы, немесе Г жиынындағы формула (яғни Bi-ң бірі), неммесе алдыңғы формулалардың тікелей салдары. Онда Аm Г формулалар жүйесінің салдары деп аталады: Г├ Аm деп белгіленеді, немесе B1,…,Bn ├ Аm деп белгіленеді. А1,..., Аm тізбегі Г жүйесіндегі Аm формуласының қорытылуы деп аталады. Г жүйесіндегі формулалар алғышарттар немесе гипотезалар деп талады, ал Аm формуласы – Г гипотезалар жүйесінен қорытылған деп аталады.
Г = Ø болған кезде, дербес жағдай деп есептеледі, яғни А тек қана аксиоманың салдары, теорема: белгіленуі├ А. Теореманың қорытылуы оның дәләлдеуі деп аталады.
Қандай да бір формулалар жүйесінің және дербес жағдайда Т теориясының барлық салдарлар жиыны осы процесс тудыратын қорытынды болады.
Bn қорытынды формула мен гипотезалар жиыны арасындағы “гипотезалар жүйесінен қорытып шығару” қатынасын “тікелей салдар болу” қатынасының транзитивті тұйықталуы ретінде қарастыруға болады.
Гипотезалар жүйесінен қорытылудың кейбір қасиеттерін қарастырайық: Г – кез - келген формулалар жиыны, А,В,С – қандай да бір формулалар болсын.
1. Бұл егер алғышартта Г-дан басқа, қандай да бір Аформуласы бар болса, онда А <Г,А> қосының салдары екенін көрсетеді. Бұл жағдайда Г жүйесін қолданбауға болады – қорытынды жалғыз А формуласынан тұрады.
2. Егер Г├ А болса, онда В├ А. Мағынасы, Г алғышартына кез – келген В формуласын қосқаннан А-ң қорытылуы өзгермейді – А формуласының қорытылуын өзгертпеуге болады.
3. Егер (Г├ А)&( Г├ В)&( А,В├ С), онда Г├ С. Егер Г жүйесінен А және В қорытылса, ал олардан С қорытылса, онда С Г жүйесінің салдары болады. Действительно, пусть А1,..., Аm, А- вывод формулы А из Г, B1,…,Bn, В вывод из Г, С1,…,Сk, С- вывод С из (А,В). тогда А1,..., Аm, А, B1,…,Bn, В, С1,…,Сk, С есть вывод С из Г.
4. Егер (Г,А├ В)&( Г├ А), онда ( Г├ В). Бұл қорытылатын гипотезадан жою ережесі. Формалды жүйе көбіне абстрактілі объектілерге символдарға, сөздерге және оларды тізбектеріне сүйенеді.
Математикалық индукция әдісі.
Толық емес индукция жиі қате қорытынды әкеліп соғады. Толық индукция әдісі тек қана шектеулі түрде қолданылады. Көптеген қызықты математикалық тұжырымдар шексіз дербес жағдайлардан тұрады, ал шексіз дербес жағдайлардың бәрін тексеріп шығу мүмкін емес. Сондықтан да ерекше әдіс – математикалық индукция әдісіне тоқталамыз.
Математикалық индукция принципі (аксиомасы).
Егер келесі екі шарт орындалса, n натурал санға тәуелді тұжырым, кез келген n үшін тура болады:
а) n =1 үшін тұжырым тура ;
б) кез келген натурал k үшін, n = k боғандағы тұжырымның дұрыстығынан n = k +1 үшін тура екендігі шығады .
Математикалық индукция әдісі бойынша дәлелдеудің мысалы.
1 мысал . Кез келген 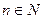 үшін теңдіктің тура екенін дәлелдеу керек.
үшін теңдіктің тура екенін дәлелдеу керек.
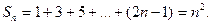
Шешуі .
а) 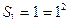 , демек, n=1 үшін тұжырым тура.
, демек, n=1 үшін тұжырым тура.
б) k – кез келген натурал сан болсын және тұжырым n=k үшін орындалсын,
яғни
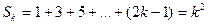 .
.
n=k+1 үшін тұжырымның дұрыстығын дәлелдейміз, яғни
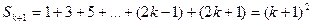 .
.
Расында, да
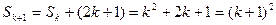 .
.
Сонымен математикалық индукция принципі бойынша кез келген n натурал мән үшін тұжырым дәлелденді.
Әдебиет: 1, 127-128 бет, 6, 185-200 бет;
Бақылау сұрақтары:
1. Аксиоматикалық теория қалай беріледі?
2. Аксиомалар және қорыту ережелері қалай анықталады?
3. Пеано аксиомалар жүйесін көрсетіңіз.
4. Толық математикалық индукция әдісінің мағынасы неде.
1. тақырып
Логикалық салдар
Мақсаты:
1. Логикалық салдар түсінігін енгізу.
2. Логикалық салдар белгілерін қарастыру.
3. Логикалық қорыту ережелерін қарастыру.
4. Силлогизм құру және оның дұрыстығын анықтауда біліктілік пен дағдыны қалыптастыру.
Жоспар:
1. Логикалық салдар.
2. Логикалық салдар белгілері.
3. Логикалық қорыту ережесі.
4. Тура және кері теоремалар.
5. Силлогизмдер.
Логикалық зерттеулердің, логикалық ой-қорытындалардың заңдылықтарын зерттейтін пікірлер алгебрасы осы бөлімнің өзегі болып табылады. Осы заңдылықтарды білу ең алдымен математикалық ғылымға қажетті. Сол білімдердің арқасында математикалық дәлелдеулер жасалады, демек математиканың дамуы болады.
Логикалық салдар түсінігі. Бір немесе бірнеше 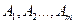 сөйлемдерінен В сөйлемі шығады деп: әр кезде,
сөйлемдерінен В сөйлемі шығады деп: әр кезде, 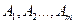 барлық сөйлемдерінің ақиқаттығынан В сөйлемі де ақиқат болатындығын айтады. Мысалы: «Егер мен жазда жұмыс істесем (А тұжырым), онда менде ақша болады (В тұжырым)». «Егер менде ақша болса (В тұжырым), онда мен магнитофон сатып аламын(С тұжырым)». «Егер мен күндіз сабақты дайындамасам (А1 тұжырым) және кешке киноға барсам(А2 тұжырым), онда ертең сабаққа дйын болмаймын (Д тұжырым)». Келтірілген пікірлердің дұрыстығы олардың мазмұнын және мағынасын талдау арқылы жүзеге асады.
барлық сөйлемдерінің ақиқаттығынан В сөйлемі де ақиқат болатындығын айтады. Мысалы: «Егер мен жазда жұмыс істесем (А тұжырым), онда менде ақша болады (В тұжырым)». «Егер менде ақша болса (В тұжырым), онда мен магнитофон сатып аламын(С тұжырым)». «Егер мен күндіз сабақты дайындамасам (А1 тұжырым) және кешке киноға барсам(А2 тұжырым), онда ертең сабаққа дйын болмаймын (Д тұжырым)». Келтірілген пікірлердің дұрыстығы олардың мазмұнын және мағынасын талдау арқылы жүзеге асады.
Математикалық логиканың (пікірлер алгебрасының) логикалық салдар сұрақтары бойынша міндеті келесі түрде анықталады: 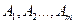 пікірлерінің мазмұнына тәуелсіз, соңғы пікір алғашқы m пікірдің салдары болуы керек. Пікірлер формалары пікірлер алгебрасының формулалары арқылы өрнектеледі. Логикалық салдар теориясы (пікірлер алгебрасы шеңберінде) F
пікірлерінің мазмұнына тәуелсіз, соңғы пікір алғашқы m пікірдің салдары болуы керек. Пікірлер формалары пікірлер алгебрасының формулалары арқылы өрнектеледі. Логикалық салдар теориясы (пікірлер алгебрасы шеңберінде) F 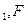
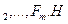 формулаларының пайда болу заңдылықтарын оқытуы керек. Алғашқы m формулалар соңғы формуламен логиқалық байымдау қатынасында болуы керек.
формулаларының пайда болу заңдылықтарын оқытуы керек. Алғашқы m формулалар соңғы формуламен логиқалық байымдау қатынасында болуы керек.
Пункттің басында келтірілген байымдауларға оралайық: А 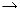 В және В
В және В  С. Оларға қатысты келесі ойқорытуды шығарамыз: «Егер А
С. Оларға қатысты келесі ойқорытуды шығарамыз: «Егер А  В және В
В және В  С, онда А
С, онда А  С». Келесі түрде айтылады: «Егер А
С». Келесі түрде айтылады: «Егер А 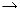 В тура және В
В тура және В 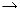 С тура болса, онда А
С тура болса, онда А 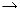 С пікірі де тура».
С пікірі де тура».
1 анықтама. Егер H (X) формуласы оның барлық X 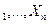 пропозиционалды айнымалыларының орнына нақты пікірлерді қойғаннан ақиқат пікірге айналса, барлық F (X), …., F
пропозиционалды айнымалыларының орнына нақты пікірлерді қойғаннан ақиқат пікірге айналса, барлық F (X), …., F  (X
(X 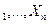 ) формулалары ақиқат пікірлерге айналса, онда H(X
) формулалары ақиқат пікірлерге айналса, онда H(X 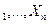 ) формуласы F
) формуласы F  (X
(X 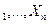 ), …., F
), …., F  (X
(X 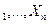 ) формулаларының логикалық салдары деп аталады. H формуласы F
) формулаларының логикалық салдары деп аталады. H формуласы F  , …, F
, …, F  формулаларының логикалық салдары келесі түрде жазылады: F
формулаларының логикалық салдары келесі түрде жазылады: F  , …, F
, …, F  =H. F
=H. F  , …, F
, …, F  формуласы H формуласының логикалық салдары үшін алғышарт деп аталады.
формуласы H формуласының логикалық салдары үшін алғышарт деп аталады.
Сонымен, F  , …, F
, …, F  =H, егер кез-келген
=H, егер кез-келген 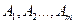 пікірлері үшін
пікірлері үшін 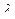 (F
(F 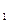 (
( 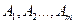 ))=1,…,
))=1,…, 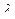 (F
(F  (
( 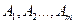 ))=1 ден
))=1 ден 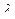 (H (
(H ( 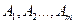 ))=1 екендігі шығады.
))=1 екендігі шығады.
Логикалық пікірлердің белгілері.
Теорема. (логикалық салдардың белгісі). H формуласы F формуласының логикалық салдары болады сонда тек сонда ғана, қашан F 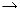 H формуласы таврология болады: F=H
H формуласы таврология болады: F=H  =F
=F  H.
H.
Теорема. Кез-келген F, …, F, H (m 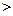 2) формулалары үшін келесі тұжырымдар мәндес:
2) формулалары үшін келесі тұжырымдар мәндес:
а) F 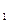 , …, F=H
, …, F=H
б) F 
 F
F 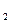 …, F=H
…, F=H
в) = (F 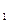
 F
F 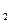 …, F)
…, F) 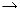 H
H
Теорема. Пікірлер алгебрасының екі формуласымәндес болады сонда тек сонда ғана, егер әрқайсысы бір-бірінің логикалық салдары болса:
F 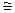 H
H 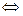 F=H и H=F
F=H и H=F
Логикалық қорыту ережелері.
1 ереже. (modus ponens)
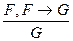
Бұл ереженің мағынасы: F алғышарттың ақиқаттығын F 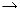 G басқа алғышарттың көмегі арқылы көрсеткеннен кейін G салдардың ақиқаттығына көшеді.
G басқа алғышарттың көмегі арқылы көрсеткеннен кейін G салдардың ақиқаттығына көшеді.
Берілген ереже қорытынды жасау ережесі деп те айтылады.
2. ереже. (modus tollens)
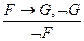
Бұл ереженің мағынасы: G алғышарттың ақиқаттығын F 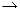 G арқылы терістеуден F –ң ақиқаттығын терістеуге көшеді.
G арқылы терістеуден F –ң ақиқаттығын терістеуге көшеді.
3 ереже . (конъюнкцияны енгізу)
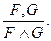
4 ереже . (конъюнкцияны жою)
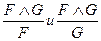
5 ереже . (дизъюнкцияны енгізу)
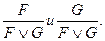
6 ереже . (контрапозиция)
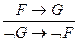
7 ереже . (шынжырлы қорыту)
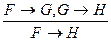
8 ереже . (алғышарттардың орнын ауыстыру)
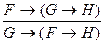
9 ереже . (алғышарттарды біріктіру және ажырату)
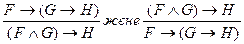
Аристотель алғаш рет логикалық байламдар және силлогизмдер туралы оқытуды негіздеді.
Аристотель және оның оқушылары силлогизм туралы түсінікті енгізді, яғни 2 пікірден үшіншісі қорытылып шығады.
1 мысал. «Барлық құстар –жануарлар»,
«Барлық торғайлар – құстар»,
демек «Барлық торғайлар –жануарлар»
Алғашқы екі сөйлем алғышарт деп, ал үшінші сөйлем қорытынды деп аталады.
Бұл жерде барлық үш сөйлем де ақиқат, қорытындының ақиқаттығы алғышарттардың ақиқаттығынан анықталған сызба бойынша шығады.
Сызба келесі түрде болады:
«Барлық В, С болады» Дұрыс түрдегі силлогизм
« Барлық А, В болады»
демек, «Барлық А, С болады».
Сондықтан осындай сызба бойынша жасалған қорытынды логикалық дұрыс деп есептеледі.
2 мысал. «Барлық квадраттар – ромб».
« Кейбір ромбтар сүйір бұрышты болады ».
Демек, «Кейбір квадраттар сүйір бұрышты болады».
Алғашқы екі пікір – дұрыс, ал қорытынды жалған, себебі құрамында логикалық қате бар.
Қорытынды келесі сызба бойынша жасалды:
«Барлық А, В болады»
« Кейбір В, С болады »
Демек, «КейбірА, С болады».
Бұл сызба ақиқат алғышарттардан жалған қорытынды береді, ал дұрыс қорытынды деп, ақиқат алғышарттардан ақиқат қорытынды алынатын сызбаларды айтады.
Логикалық қорытындылар қандай да бір анықталған сызбалар бойынша жасалады.
Силлогизмнің дұрыстығын тексеру үшін, жиындар теориясына негізделген әдісті қолданамыз.
«Барлық А, В болады» деген пікір, А жиыны В жиынының ішкі жиыны дегенді білдіреді.
3. « Барлық А , В болады »  А
А  В.
В.
А  В
В
4. « Кейбір А , В болады »  А
А  В
В  .
.
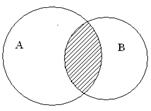
А  В
В 
5. « Ешқандай А , В болмайды » 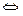 А
А  В
В 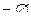 .
.

А  В
В 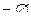
6. « Кейбір А , В емес » 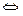 А\В
А\В  .
.
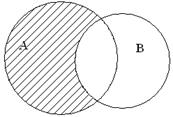
А\В 
Логикалық пікірлер, жиындарға ұқсас, Венн диаграммалары арқылы бейнелеген ыңғайлы.
1 мысал. А  В
В  В
В 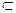 С
С 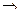 А
А  С.
С.

7. мысал. А  В
В  В
В  С
С 
 А
А  С
С 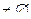 .
.
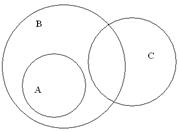
қорытынды – жалған .
Ә дебиет: 1, 123 бет,6, 42-51 бет
Бақылау сұрақтары :
1.Логикалық салдар қалай анықталады?
2. Логикалық салдарлар белгілерін көрсетіңіз.
3. Қандай логикалық ойқорытуларды білесіз?
4.Тура және кері теоремалар қалай анықталады?
5. Силлогизмдер құратын негізгі тұжырымдар қандай.
14 тақырып
Пікірлердің есептелімі
Мақсаты :
1.Пікірлер есептелімін аксиоматикалық түрде құру.
2. Пікірлер есептелімінің қорыту ережесін қарастыру.
3. Үшіншіні жою заңын дәлелдеу.
4. Дедукция теоремасын және оның салдарларын қолдану.
5. Тавталогиялардың қорытылуы туралы теоремалар.
6. Дедукция теоремасын және қорыту ережелерін қолдануда біліктілік пен дағдыны қалыптастыру.
Жоспар :
1. Символдар, формулалар және пікірлер есептелімінің аксиомалары.
2. Пікірлер есептелімінің қорыту ережесі.
3. Дедукция теоремасы және оның салдарлары.
4. Тавталогиялардың қорытылуы туралы теоремалар.
Әрбір есептелудің құрамында қолданылатын символдардың, есептеу формулаларының, ақиқаттық формулалардың анықтамасының сипаттамасы болады. Келесі жүйені қарастырамыз:
1. Пікірлер есептелімінің символдары:
-индекстері бар және индекстері жоқ айнымалылардың символдары:
X, Y ,…, Xi,…;
- Екі логикалық символдар: ˉ және v ;
- оң жақ және сол жақ жақшалар «(« и «)».
2. Пікірлер есептелімінің формулалары:
а) барлық айнымалылар;
б) егер А, В – формулалар болса, онда (  ) және (A v В) – да формулалар.
) және (A v В) – да формулалар.
Берілген анықтама бойынша , егер А, В, С – формулалар болса, онда A v 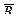 v С – формула емес (себебі қажетті жақшалар жетіспейді), ал
v С – формула емес (себебі қажетті жақшалар жетіспейді), ал 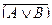 - формула,
- формула, 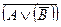 - формула,
- формула,  - да формула. Жазылу түрін қысқарту және ықшамдау үшін формулалардағы сыртқы жақшаларды алып тастауға болады.
- да формула. Жазылу түрін қысқарту және ықшамдау үшін формулалардағы сыртқы жақшаларды алып тастауға болады.
ˉ және v символдары пікірлер логикасында терістеу және дизъюнкция амалдары (немесе функциялары) ретінде қарастырылады. Ыңғайлылық үшін басқа да логикалық амалдарды енгіземіз:
А & В ≡ 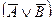
A→B ≡ 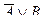
Бұл белгілерді аксиомалық жүйенің элементтері емес, қысқаша жазылуы түрінде қарастырамыз.
5. Пікірлер есептелімінің аксиомалары (А, В, С – кез келген формулалар):
A1. 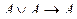
А2. 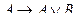
A3. 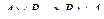
A4. 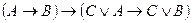
Осы аксиоамалардың әрқайсысын есептелудің негізгі логикалық символдары арқылы жазуға болады. Мысалы, А3 аксиомасы келесі түрде жазылады: 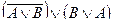
А1-А4 өрнектері аксиомалардың сызбасы деп аталады. Бұл жерде А,В,С – ның орнына кез келген формулаларды қоюға болады.
4. Жалғыз қорыту ережесі – силлогизм modus ponens (қысқаша m.p.), жазылу түрі, 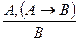 , мұнда с ызықтың үстінде алғышарттар, ал сызықтың астында - қорытынды.
, мұнда с ызықтың үстінде алғышарттар, ал сызықтың астында - қорытынды.
Аксиоматикалық теорияда қоытылу түрінде бұл ереже келесі түрде жазылады: 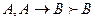
Жүйенің қалай жұмыс жасайтындығын көрсету үшін, үшіншіні жою заңының дәлелдеуін келтіреміз.
1. 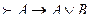 - А2 аксиомасы
- А2 аксиомасы
2. 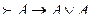 -1-ден, В орнына А қойылған
-1-ден, В орнына А қойылған
3. 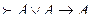 - А1 аксиомасы
- А1 аксиомасы
4. 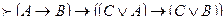 - А4 аксиомасы
- А4 аксиомасы
5 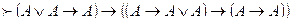 -4-тен, А-ның орнына AvA қойылған, В орнына A, С орнына
-4-тен, А-ның орнына AvA қойылған, В орнына A, С орнына 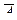 ( р→q – қысқаша
( р→q – қысқаша 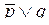 )
)
6. 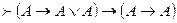 -3 және 5- тен m.p. ережесі бойынша
-3 және 5- тен m.p. ережесі бойынша
7. 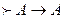 яғни
яғни 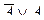 - 2 және 6-дан m.p. ережесі бойынша
- 2 және 6-дан m.p. ережесі бойынша
8. 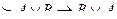 - A3 аксиомасы
- A3 аксиомасы
9. 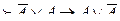 -8-ден; A орнына
-8-ден; A орнына 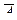 және A орнына B қойылған
және A орнына B қойылған
10. 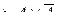 - 7 және 9 –дан m.p. ережесі бойынша
- 7 және 9 –дан m.p. ережесі бойынша
Соңғы формуланың мағынасы, екі қарама-қарсы пікірден, яғни А және 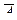 -дің кем дегенде біреуінің ақиқаттығынан, олардың дизъюнкциясы ақиқат болғандықтан ақиқат екені шығады.
-дің кем дегенде біреуінің ақиқаттығынан, олардың дизъюнкциясы ақиқат болғандықтан ақиқат екені шығады.
4 формуласынан 5 формуласына өтуді көрсетеміз:
4 формуласы 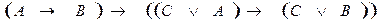
↓ ↓ ↓ ↓ ↓ ↓
ауыстыру 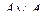 A
A 
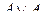
 A
A
Қорытынды 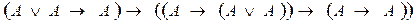
ауыстыру < 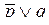 > <
> < 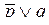 >
>
дизъюнкцияны импликацияға алмастыру 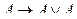
<p→q> <p→q>
5 формуласы 
Пікірлер есептелімі үшін 1-4 жалпы қасиеттерден басқа келесі қасиет те орындалады
6. Егер 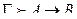 және
және 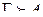 , онда
, онда 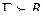
Дедукция т еорема сы. Егер А, В формулалары және Г жүйесі үшін, Г, 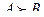 орындалса, онда
орындалса, онда 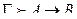 орындалады.
орындалады.
Дедукция теоремасын қолдану «егер А , онда В « пікірінің ақиқаттығын көрсетеді.
Дедукция теоремасының салдарлары.
1 салдар. (силлогизм ережесі). 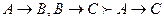 .
.
2 салдар . 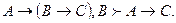
3 салдар . Егер 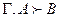 және
және 
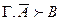 болса, онда
болса, онда 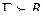 (егер Г жүйесінен А формуласын қосқаннан В формуласы қорытылса және
(егер Г жүйесінен А формуласын қосқаннан В формуласы қорытылса және 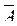 формуласын қосқаннан В формуласы қорытылса, онда Г жүйесінен В формуласы қорытылады ).
формуласын қосқаннан В формуласы қорытылса, онда Г жүйесінен В формуласы қорытылады ).
Теорема (тавтологияның қорытылуы туралы). Пікірлер есептелімінің А формуласы қорытылымды сонда тек сонда ғана, егер ол пікірлер логикасында ақиқат (тавтология) болса (яғни 1-ге теңбе-тең буль функциясы ретінде көрсетілсе).
Әдебиет : 1, 108-111; 6, 97-105 бет; 17, 17-34 бет.
Бақылау сұрақтары :
1. Пікірлер есептелімінің фомулаларын және символдарын атаңыз.
2. Пікірлер есептелімінің қандай аксиомаларын білесіз?
3. Қорыту ережелерін атаңыз.
4. Дедукция теоремасын және оның салдардарын айтыңыз.
5. Тавталогиялардың қорытылуы туралы теореманы айтыңыз.
15 тақырып
Предикаттар логикасы
Мақсаты:
1. Предикаттар түснігін енгізу.
2. Предикаттар кластарын және қасиеттерін қарастыру, олардың өзара байланысы.
3. Предикаттарға қолданылатын кванторлық операцияларды енгізу.
4. Предикаттарға амалдар қолданудағы біліктілік пен дағдыны қалыптастыру.
Жоспар :
1. Предикаттар.
2. Предикаттардың классификациясы.
3. Кванторлар.
Предикат тар . Негізгі түсініктер .
Предикат түсінігі пікірлер түсінігінің жалпылауы болып табылады. Математикада анықталған тұжырымның ақиқат немесе жалған екендігі оның құрамындағы айнымалыға тәуелді болатын сөйлемдер тжиі кездеседі.
Мысалы: 1) «х+2=5» , х 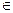 Z
Z
2) «n-жай сан»
3) «х өзені Байкал көліне құяды»
осы пікірлердің әрқайсысы, айнымалының орнына қандай-да бір нақты мәнді қойғаннан ақиқат немесе жалған пікірге айналады.
1 анықтама. М1,…,Мn жиындарында анықталған n орынды предикат деп, құрамында х1,…,хn айнымалылардың орнына сәйкес М1,…,Мn жиындарынан кез келген нақты мәндерді қойғаннан пікірге айналатын сөйлемді айтады.
Белгіленуі Р(х1,…,хn).
х1,…,хn – заттық айнымалылар, М1,…,Мn жиындаының элементтері – нақты айнымалылар деп аталады.
М1,…,Мn жиындарында анықтылған n орынды Р(х1,…,хn) предикат n аргументті функция болып табылады. Предикат – функция-пікір деп те аталады.
Мысалы: «х2+у2≤9» - екі орынды предикат. RxR жиынында берілген.
(2;1) «22+12≤9» - ақиқат
(3;3) «32+32≤9» - жалған.
Предикаттар к лассификация сы
2 анықтама. М1,…,Мn жиындарында анықталған Р(х1,…,хn) предикат:
1) егер х1,…,хn айнымалылардың орнына М1,…,Мn жиындарынан сәйкес а1,…,аn нақты айнымалыларды қойғаннан Р (а1,…,аn) ақиқат пікірге айналса, онда ақиқат предикат деп аталады;
2) Р (а1,…,аn) жалған пікірге айналса, жалған предикат деп талады;
3) Орындалатын предикат (жалған да, ақиқат та)болса; Мысалдар .
1) R жиыныда анықталған бір орынды предикат «sin2x+cos2x=1», -ақиқат.
2) R- жиыныда анықталған «х2+у2<0»-екі орынды предикат жалған.
3) «х өзені Байкал көліне құяды» - бір орынды предикат - орындалатын, себебі берілген предикатты ақиқат пікірге айналдыратын басқа да, өзен (Баргузин) бар және жоққа шығарылатын, себебі «Ангара» жалған пікірге айналдырады.
Анықтама: М1,…,Мn жиындарында анықталған Р (х1,…,хn) предикаттың ақиқиттық жиыны деп берілген предикат х1=a1, х2=a2,…, хn=an мәндерінің орнына қойғанда Р (х1,…,хn) пікірі ақиқат болатындай реттелген (а1,…,аn) n-жүйелер жиынтығы аталады. Мұндағы, а1 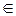 М1, …, аn
М1, …, аn 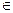 Мn. Бұл жиын Р+ деп белгіленеді.
Мn. Бұл жиын Р+ деп белгіленеді.
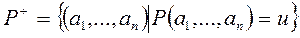
Мысалдар:
1) R жиынында берілген екі орынды S (х,у): «х2+у2=9» предикаттың ақиқаттық жиыны, центрі координаталар бас нүктесінде орналасқан және радиусы 3-ке тең шеңбер бойында орналасқан жазықтықтағы нақты сандардың қостар жиыны.
2) А (х): « 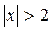 »-R гі бір өлшемді предикат.
»-R гі бір өлшемді предикат.
А+= 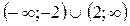
М1,…,Мn жиындарында берілген Р (х1,…,хn) n- орынды предикат:
I. ақиқат 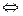
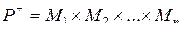
II. жалған  Ø
Ø
III. орындалатын  Р+
Р+  Ø
Ø
IV. жоққа шығарылатын 
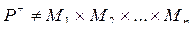
Предикаттарға қолданылатын к вантор лық операциялар
Предикаттарға пікірлерге қолданылатын ( 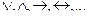 ) амалдардан басқа, олардан өзгеше басқа амалдар қолдануға болады.
) амалдардан басқа, олардан өзгеше басқа амалдар қолдануға болады.
Бұл – предикаттарға қолданылатын екі квантолық операциялар: жалпылау кванторы және табылу кванторы.
Бір орынды предикаттан пікір алу үшін, оның айнымалысының орнына предикаттың берілген облысынан бір мәнді қою керек.
Осылайша айналдырудың тағы бір тәсілі бар – бұл предикатқа жалпылау кванторымен және табылу кванторымен байланыстыру операциясын қолдану.
Бұл операциялардың әрқайсысы бір орынды предикатқа, берілген предикатқа тәуелді ақиқат немесе жалған мән қабылдайтын пікірді сәйкестендіреді (яғни бір орынды предикат нөлдік предикатқа айналады).
Анықтама: Жалпылау кванторымен байланыстыру операциясы деп, М жиынында анықталған әрбір бір орынды Р (х) предикатқа 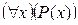 деп белгіленетін пікірді сәйкестендіретін ережені атайды. ( «барлық х үшін Р (х) орындалады» деп оқылады),
деп белгіленетін пікірді сәйкестендіретін ережені атайды. ( «барлық х үшін Р (х) орындалады» деп оқылады),
Бұл пікірлердің логикалық мәндері келесі формула бойынша анықталады:
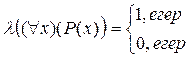
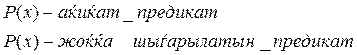
Мысал. 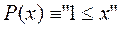 - ақиқат предикат
- ақиқат предикат
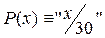 N сандар жиыныда –жоққа шығарылатын предикат
N сандар жиыныда –жоққа шығарылатын предикат
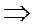 жалпылау кванторымен байланыстыратын операция, бірінші жағдайда ақиқат пікір, ал екінші жағдайда жалған пікірге айналады.
жалпылау кванторымен байланыстыратын операция, бірінші жағдайда ақиқат пікір, ал екінші жағдайда жалған пікірге айналады.
Қорытынды: егер берілген предикат М жиынының барлық элеметтеріне ақиқат болса, онда 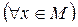 жалпылау кванторымен байланыстырғаннан:
жалпылау кванторымен байланыстырғаннан:
р (х) оны ақиқат пікірге айналдырады.
Бұл жерде х айнымалысы «байланысты» болады, кәдімгі мағынадағы айнымалы болмайды.
Анықтама: Табылу кванторымен байланыстыру операциясы деп, М жиыныда анықталған әрбір бір орынды Р (х) предикатқа ( 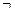 х)(Р(х)) деп белгіленетін пікірді сәйкестендіретін ережені атайды. ( «Р(х) орындалатындай, х табылады» деп оқылады), Бұл пікірлердің логикалық мәндері келесі формула бойынша анықталады:
х)(Р(х)) деп белгіленетін пікірді сәйкестендіретін ережені атайды. ( «Р(х) орындалатындай, х табылады» деп оқылады), Бұл пікірлердің логикалық мәндері келесі формула бойынша анықталады:
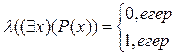
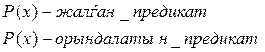
Мысал: Р (х): «х=х+1» - жалған предикат
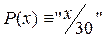 - орындалатын предикат
- орындалатын предикат
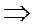 табылу кванторымен байланыстыратын операция, бірінші жағдайда жалған пікір, ал екінші жағдайда орындалатын пікірге айналады.
табылу кванторымен байланыстыратын операция, бірінші жағдайда жалған пікір, ал екінші жағдайда орындалатын пікірге айналады.
Қорытынды: егер берілген предикат М жиынының кем дегенде х 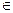 М бір элементі үшін ақиқат болса, онда
М бір элементі үшін ақиқат болса, онда 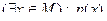 табылу кванторымен байланыстырғаннан: р (х) оны ақиқат пікірге айналдырады.
табылу кванторымен байланыстырғаннан: р (х) оны ақиқат пікірге айналдырады.
Бұл амалдардың ерекшеліктері .
а) 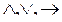 логикалық операциялар бір немесе бірнеше предикаттарға жаңа предикаттар сәйкестендірді, ал квантолық операциялар бір орынды предикатқа пікірді сәйкестендіреді.
логикалық операциялар бір немесе бірнеше предикаттарға жаңа предикаттар сәйкестендірді, ал квантолық операциялар бір орынды предикатқа пікірді сәйкестендіреді.
б) егер бірорынды Р(х) предикат М={a1,…,аk} ақырлы жиында берілсе, онда
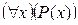 пікірі
пікірі
Р (а1)  …
…  Р (а k) конъюнкцияға эквивалентті
Р (а k) конъюнкцияға эквивалентті
( 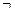 х)(Р(х)) пікірі
х)(Р(х)) пікірі
Р (а1) 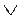 …
… 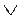 Р (а k) дизъюнкцияға эквивалентті
Р (а k) дизъюнкцияға эквивалентті
Әдебиет : 1,118-123 бет,17, 127-141 бет,3, 65-89 бет,5, 258 бет
6,122-141 бет
Бақылау сұрақтары :
1. Предикаттың анықтамасын беріңіз.
2. Предикаттардың қандай түрлерін білесіз?
3. Әртүрлі предикаттар арасындағы байланысты көрсетіңіз.
4. Предикаттың ақтқаттық жиыны қалай анықталады?
5. Қандай кванторлық операцияларды білесіз?
6. Осы операциялардың ерекшелігін көрсетіңіз.
7. Байланысты және байланысты емес айнымалылар түсінігін беріңіз.
16 тақырып
А лгоритм дер теори ясының э лемент тері
Мақсаты :
1. Алгоритмдер түсінігін енгізу.
2. Қарапайым сандық функциялардың есептелуін қарастыру.
3. Тьюринг машинасының анықтамасын енгізу.
4. Тьюринг машинасын сөздерге қолданудағы дағды мен біліктілікті
қалыптастыру.
Жоспар:
1.Алгоритм түсінігі.
2.Есептелетін функциялар.
3. Тьюринг машинасы.
1 Алгоритм түсінігі
Алгоритмдер мысалдарын талдау арқылы, оларға тән жалпы қасиеттер мен ерекшеліктерді анықтаймыз.
1) Кез келген алгоритмде алғашқы берілгендер бар болады, олар арқылы анықталған ізделінді қорытындылар алынады.
2) Әрбір алгоритмді қолдану қадамдар деп аталатын, кейбір элементар іс-әрекеттер тізбегінен тұратын, дискретті тізбек арқылы жүзеге асады. Оларды қолдану процесі алгоритмдік процесс деп аталады, осылайша дискреттік қасиеттің ерекшеліктері пайда болады.
3) Алгоритмнің басты қасиетінің бірі оның көптік сипаты, яғни оны бастапқы берілгендердің өте көп класына қолдану мүмкіндігі, демеккез келген алгоритм арқылы көптеген мәселелерді шешуге болады, яғни біртипті есептерді шығаруға болады.
4) Алгоритмдер үшін қажетті шарт оның анықталғандығы болып табылады. (яғни, кім рындауына тәуелсіз, қорытынды кез келген жағдайда алынады)
Алгоритм – қандай-да бір берілген кластың барлық есептерін шығаруға арналған, анықталған ретте орындалатын нұсқаулар жүйесі.
«Алгоритм» термині ұлы ортаазиялық ғалым Мухаммед аль – Хорезм есімі арқылы шыққан ( IX ғ).
Есептелетін функци ялар
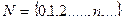 натурал сандар жиынында берілген немесе оның ішкі жиыныда берілген және N жиынынан мәндер қабылдайтын, бір аргументке немесе бірнеше аргументке тәуелді
натурал сандар жиынында берілген немесе оның ішкі жиыныда берілген және N жиынынан мәндер қабылдайтын, бір аргументке немесе бірнеше аргументке тәуелді 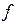 функциясын қарастырамыз.
функциясын қарастырамыз.
1 анықтама.  функциясы есептелімді деп аталады, егер оның барлық аргументтерінің мәндерін есептейтін және тоқтаусыз жұмыс жасайтын алгоритм табылса.
функциясы есептелімді деп аталады, егер оның барлық аргументтерінің мәндерін есептейтін және тоқтаусыз жұмыс жасайтын алгоритм табылса.
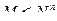 болсын.
болсын.
2 анықтама. Егер кез келген элемент берілген М жиынына тиісті ме, жоқ па екенін анықтайтын алгоритм тбар болса, онда М жиыны шешілімді жиын деп аталады.
Егер 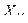 функциясы М жиыныда берілсе және {0,1} екі элементті жиыннан мәндер қабылдаса, онда
функциясы М жиыныда берілсе және {0,1} екі элементті жиыннан мәндер қабылдаса, онда 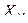 функциясы М жиынының сипаттамалық функциясы деп аталады және келесі түрде анықталады:
функциясы М жиынының сипаттамалық функциясы деп аталады және келесі түрде анықталады:
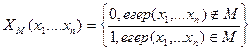
М жиыны шешілімді ó егер оның  сипаттамалық функциясы есептелімді болса.
сипаттамалық функциясы есептелімді болса.
3 анықтама. М  N жиыны саналамды (рекурсивті немесе алгоритмді) деп аталады, егер М жиыны немесе бос жиын болса немесе оның мәндер жиыны қандай да бір есептелімді функция болса, басқаша айтқанда оның барлық элементтерін тізбектеп табатын алгоритм табылса.
N жиыны саналамды (рекурсивті немесе алгоритмді) деп аталады, егер М жиыны немесе бос жиын болса немесе оның мәндер жиыны қандай да бір есептелімді функция болса, басқаша айтқанда оның барлық элементтерін тізбектеп табатын алгоритм табылса.
Мысал . М={1,4,9,…..} натурал сандардың квадраттары жиынын қарастырамыз. Ол 1,2,3…. сандарын біртіндеп квадраттау арқылы алынады, яғни саналымды жиын.
Басқаша айтқанда, М=  жиыны
жиыны 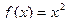 есептелімді функцияның мәндер жиыны болып табылады.
есептелімді функцияның мәндер жиыны болып табылады.
Бұл жиын шешілімді де болады: қандай да бір сан берілген жиынға тиісті ме жоқ па тексеру үшін, оны жай көбейткіштерге жіктеу керек.
Кез келген шешілімді жиын саналымды, бірақ кері тұжырым дұрыс емес.
Тьюринг машинасы
Бұл түсінік ағылшын математигінің атымен аталған, алғаш рет 1937 жылы, бірінші ЭЕМ пайда болғанға дейін 9 жыл бұрын берілген.
Тьюринг машинасының анықтамасы
Тьюринг машинасы кәдімгі машина емес, математикалық (елестететін) машина. Бұл функция, туынды, интеграл және т.с.с. математикалық объектілер.
Басқа да математикалық түсініктер сияқты, Тьюринг машинасы да кейбір нақты процестердің модельдерін жасайды.
Тьюрин машинасын автоматты жұмыс істейтін қондырғы түрінде көрсету ыңғайлы.
Әрбір дискретті кезеңде қондырғы қандай да бір күйде бір ұяшықтың қрамын лента арқылы қарап шығып, бір қадам жасайды. Жаңа қадам жасаған кезде қаралатын ұяшықтың құрамын сол жақтан және оң жақтан өзгертіп, басқа күйге түседі. Әрбір қадам берілген команда бойынша жүзеге асады. Барлық командалар жиынтығы Тьюринг машинасының программасын көрсетеді.
Тьюринг машинасының сипаттамасы.
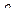 - Тьюринг машинасының белгіленуі.
- Тьюринг машинасының белгіленуі.
Тьюринг машинасы 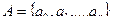 - сыртқы алфавит деп аталатын және осы алфавит құратын ақырлы белгілерден тұрады.
- сыртқы алфавит деп аталатын және осы алфавит құратын ақырлы белгілерден тұрады.
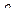 лентасының әрбір ұяшығына, әрбір ақырлы уақытта А алфавиттен бір ғана символ жазылады.
лентасының әрбір ұяшығына, әрбір ақырлы уақытта А алфавиттен бір ғана символ жазылады.
А алфавитте «бос әріп» бар деп есептейміз және ол бос ұяшықта жазылған болсын. «Бос әріп» немесе бос ұяшықтың символы 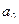 деп белгіленсін. Лента екі жағынан да шектелмеген деп ұйғарылады, бірақ әрбір уақыт кезеңінде оған бос емес әріптердің ақырлы саны жазылады.
деп белгіленсін. Лента екі жағынан да шектелмеген деп ұйғарылады, бірақ әрбір уақыт кезеңінде оған бос емес әріптердің ақырлы саны жазылады.
Әрбір уақыт кезеңінде  машинасы ақырлы ішкі күйлердің бірінде болады,
машинасы ақырлы ішкі күйлердің бірінде болады, 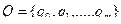 - ішкі күйлер жиынтығы болсын.
- ішкі күйлер жиынтығы болсын.
Олардың арасында 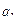 - бастапқы күйі, ал
- бастапқы күйі, ал 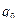 қорытынды немесе тоқтау кезеңіндегі күйі.
қорытынды немесе тоқтау кезеңіндегі күйі.
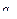 жағдайында машина жұмыс істеуді бастайды, ал
жағдайында машина жұмыс істеуді бастайды, ал 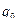 жағдайында машина тоқтайды.
жағдайында машина тоқтайды.
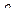 Тьюринг машинасының жұмысы программамен (функционалды схемамен) анықталады. Программа командалардан тұрады.
Тьюринг машинасының жұмысы программамен (функционалды схемамен) анықталады. Программа командалардан тұрады.
Әрбір команда T (I , j) ( I =1,2,…m; j=0,1,….n) келесі өрнектердің бірі болып табылады.
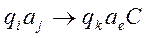
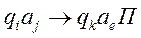
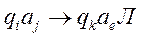
1 өрнегіндегі С символы көбіне жазылмайды.
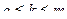 ;
; 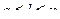
Тьюринг машин асының жұмысы . Қандай да бір уақыт кезеңінде ( 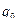 жағдайынан басқа кезде) машина оның
жағдайынан басқа кезде) машина оның 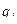 және
және 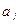 лентадағы символы арқылы қадам жасайды.
лентадағы символы арқылы қадам жасайды.
Қадамның мазмұны: T( I , j ): 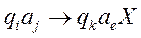 командасына сәйкес, мұндағы
командасына сәйкес, мұндағы 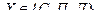 .
.
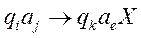 командасы бойынша, машина qi жағдайында
командасы бойынша, машина qi жағдайында 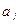 әрпі жазылған ұяшықты қарайды, содан кейін машина
әрпі жазылған ұяшықты қарайды, содан кейін машина 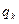 жағдайына ауысады, қаралған ұяшықты
жағдайына ауысады, қаралған ұяшықты 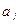 әрпін өшіріп, онда
әрпін өшіріп, онда 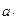 әрпін енгізеді. Х=П, Х=Л байланысты машина оң жақ, немесе сол жақ ұяшықты қарастырады. Егер ештеме жазылмаса, сол ұяшықты қарайды.
әрпін енгізеді. Х=П, Х=Л байланысты машина оң жақ, немесе сол жақ ұяшықты қарастырады. Егер ештеме жазылмаса, сол ұяшықты қарайды.
Осы командаларды орындағаннан кейін, машина qkal→qras орындайды, т.с.с.
Әдебиет: 17, 254 бет,6,209-226 бет
Бақылау сұрақтары:
1. Алгоритм түсінігін беріңіз.
2. Қандай функция есептелінетін деп аталады?
3. Қандай жиын шешілімді деп аталады?
4. Тьюринг машинасының сипаттамасын беріңіз.
Дата добавления: 2018-09-20; просмотров: 1616; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
