Глава 2. Интерполяция степенными и тригонометрическими многочленами. Теорема В.А. Котельникова об отсчётах. Ортогональные функции на вещественной прямой

Принципиальная схема работы системы связи выглядит так, как показано на рис. 1.

Сообщение

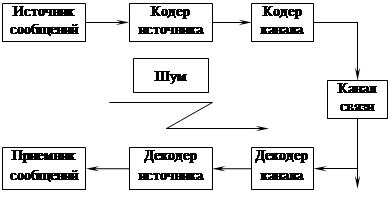
Рис.1. Принципиальная схема системы связи (Передача или хранение данных).

Кодер канала получает на вход выходной сигнал кодера источника и заменяет его одним из сигналов кода. Сигналы кода – заранее спроектированные сигналы, устроенные так, чтобы их можно было легко отличить друг от друга при искажениях, которые накладывает шум в канале. Проектирование таких сигналов – это одна из важнейших задач разработки систем связи.

Рассмотрим, как решается такая задача сначала в случаях, когда об исходном сигнале много известно.

1. Допустим, что исходный сигнал – это обычный многочлен степени n–1. Тогда мы можем восстановить сигнал, зная его значения в n различных точках. Решение здесь дает хорошо известная интерполяционная формула Лагранжа:

(2.1)

И задача решается однозначно.

2. Допустим, что сигнал – это тригонометрический многочлен порядка и заданы его значения в точках , т.е. мы хотим восстановить сигнал по 2n+1 значению в точках равномерно расположенных на отрезке .

Решение. Рассмотрим тригонометрический многочлен, соответствующий ядру Фейера:

. (2.2)

Положим в (2.2) тогда:

При , получим:

При получим правильный 2n+1-угольник, вписанный в единичную окружность, как показано на рис. 2.

Рис. 2.

Сумма всех векторов с началом в центре и концами в вершинах равна нулю, т.к. она инвариантна относительно вращения на угол , поэтому проекция этой суммы на любую ось, также равна нулю. В частности, проектируя на ось 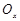, получим:

Т.е. при эта сумма равна нулю. Аналогичные рассуждения показывают, что это верно также при . Отсюда немедленно следует, что сумма:

(2.3)

дает решение поставленной задачи. Это решение также единственно. Соотношение (2.3) играет ключевую роль в спектральном анализе временных рядов любой природы. Здесь для определения решения требуется уже 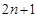значение функции – а это всего лишь многочлен, хотя и тригонометрический. Здесь уместно задаться следующим вопросом: не получится ли так, что, если нам несколько меньше известно о природе сигнала, то потребуется бесконечно много данных для его однозначного восстановления? На самом деле ситуация обстоит не так кошмарно как это может показаться. И некоторый, достаточно естественный выход, здесь будет найден.

Задача. Запишите (2.3) в виде отрезка обычного ряда Фурье по синусам и косинусам.

Указание. Воспользуйтесь формулой представления ядра Фейера через сумму косинусов. Разложите косинусы разности по известной тригонометрической формуле и сгруппируйте слагаемые. Ответ можно найти, например, в [11], а также в типовых пакетах компьютерных программ по спектральному анализу.

Вернемся теперь к тригонометрическим многочленам.

3. Число точек удается уменьшить, если задать явный вид многочлена. Допустим, что сигнал – это тригонометрический многочлен такого вида:

(2.4)

тогда его можно однозначно восстановить по значениям .

В точках ( , т.е. по 2n-значениям.

Решение. Рассмотрим функцию:

т.е. это тригонометрический многочлен. Это можно показать методом математической индукции. Более того, из предыдущего доказательства п. 2 можно увидеть, что:

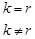, где k и r = 0, 1, 2, …, 2n–1.

Поэтому искомое решение имеет вид:

(2.5)

Кроме того, если выполнено еще одно дополнительное условие:

то порядок полинома равен n–1 или меньше, что легко видеть из (2.5).

4. Можно задать вдвое меньше значений самой функции, но при этом должны быть заданы значения производной от полинома в тех же точках. Например, можно решить такую задачу: восстановить тригонометрический полином вида:

, (2.6)

который в точках принимает значение y_r а его производная принимает значение . И здесь , т.е. n штук, т.е. 2n значений. Здесь вспомогательные функции выглядят так:

, (2.7)

(2.8)

где .

При этом выполнены такие соотношения:

(2.9)

Ответ выглядит довольно устрашающе:

. (2.10)

Таким образом, для случая полиномов задача интерполяции всегда точно разрешима, причем однозначно, заданием значений самой функции или ее производных. Требуемое число значений такое же, как и число неизвестных коэффициентов в искомой форме полинома.

Однако, как следует поступать, когда задан произвольный сигнал, а не полином? Кроме того, этот сигнал может быть задан на любом сколь угодно длинном участке времени. Если бы этот участок был фиксированным, то непрерывную функцию можно было бы аппроксимировать сколь угодно точно полиномом – по теореме Вейерштрасса это возможно только на конечном интервале. Но в случае произвольного сигнала интервал может быть любым и, по существу, нам нужна хорошая аппроксимация на всей вещественной оси.

Один из выходов состоит в том, чтобы использовать удачные свойства функции:

. (2.11)

Оказалось, что если сигнал может быть представлен в виде обобщенного ряда Фурье вида:

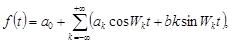(2.12)

где частоты колебаний т.е. принадлежит некоторому заданному конечному диапазону частот то можно представить в виде такого «гармонического ряда», т.е. ряда по гармоникам всё более высоких частот:

Если считать, что при , то в указанном выше ряде остается только конечная сумма, которая определяется значениями функции в точках:

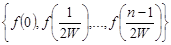что позволяет кодировать функцию достаточно общего вида с помощью n-мерного вектора, аналогично тому, как это делается в формуле Лагранжа из п. 1, т.е. нужно только n значений функции. Правда, теперь это равенство не точное, а только приближенное. Качество аппроксимации определяется узостью «окна», т.е. тем, на сколько мал интервал . Это собственно и есть содержание теоремы Котельникова. Основной недостаток метода состоит в том, что колебания оконной функции, т.е. их частота не зависит от частоты колебаний самого сигнала. Эту проблему удается частично, а в некоторых случаях и полностью решить, используя современную теорию всплесков (wavelets), построенную в пионерских работах Ива Мейера и его сотрудников из INRIA (Версаль). Начало этой теории относится приблизительно к 1985 году и сейчас в области прикладных аспектов ее можно считать уже полностью построенной, т.к. основные результаты внедрены в стандарты систем цифровой связи.

Доказательство теоремы Котельникова основано на одном забавном комбинаторном фокусе, обыгрывающем свойство ортогональности системы синусов и косинусов, замеченное еще Фурье.

Теорема. Пусть функция 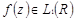и разлагается в ряд из гармоник с частотами, принадлежащими и ее преобразование Фурье аналитическая функция, тогда представима в виде следующего ряда:

. (2.13)

Доказательство. Из условия (i)следует, что f(z) можно представить в виде интеграла Фурье в таком виде:

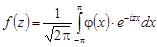. (2.14)

Из условия (ii) – j(x) представимо в виде ряда Фурье, мы запишем его в комплексной форме:

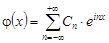(2.15)

Подставим теперь (2.15) в (2.14) и поменяем порядок суммирования и интегрирования – это и есть комбинаторный момент, считая, что это можно сделать. Если бы интеграл был конечной суммой и ряд в (2.15) также был конечным, то это всегда можно сделать. Получим:

(2.16)

Вычислим отдельно интеграл в (2.16):

(2.17)

С учетом (2.17) очень легко найти 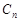. В самом деле, при все слагаемые в ряде (2.16) равны 0 кроме 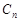, получим:

т.е.

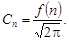(2.18)

В этом и состоит «фокус». Подставим теперь найденное 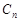в (2.16), получим:

(2.19)

Это и есть требуемое равенство (2.13) и теорема доказана.

Возможно, что все оказалось так красиво лишь потому, что мы наложили слишком сильное условие в нашей теореме. Может быть, вообще подходящих функций просто не существует? Однако, к счастью, это не так. Исследуя эту ситуацию, Р. Пэли и Н. Винер обнаружили огромный класс функций, для которых наша теорема справедлива – это, так называемые, целые функции экспоненциального типа. Более того, для этих функций справедлива импликация , т.е. второе условие в нашей теореме следует из первого и может не указываться в формулировке теоремы. Подробное изложение см. Н.Винер, Р. Пэли «Преобразование Фурье в комплексной области», М. Наука, 1964 г. Метод Пэли-Винера имеет многочисленные приложения в теории функций и даже в теории чисел, здесь речь идет о дзета-функции Римана и ее нулях.

По видимому, удивительные свойства функции до конца не изучены. Существенное продвижение в этом направлении получили киевские математики В.Л. Рвачев и В.А. Рвачев «Неклассические методы теории приближений в краевых задачах», Киев, Наукова Думка, 1979 г. Однако, редко кому удавалось справиться с неимоверной выкладочной сложностью развитой ими теории. Попытка французских математиков из INRIA в 1997 году устроить семинар по этой монографии, также ни к чему не привела. Поэтому в настоящее время теория сигналов и приложения используют более приемлемый аппарат всплескового анализа. В.Л. Рвачев и В.А. Рвачев, основываясь на некоторых специальных свойствах функции ввели специальную функцию – решение функционального дифференциально-разностного уравнения

(2.20)

причем имеет носитель на отрезке [–1, 1]:

(2.21)

и обладает очень сильными аппроксимационными свойствами. В то же время во всех двоично-рациональных точках отрезка [–1, 1] эта функция определяет многочлен, а во всех остальных точках она не аналитична, т.е. ее ряд Тейлора расходится.

Вернемся теперь к интерполяционной формуле Лагранжа п. 1 предыдущей лекции. Обозначим:

(2.22)

тогда понятно, что:

(2.23)

поэтому формулу Лагранжа можно переписать в виде:

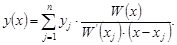(2.24)

Если при некоторой функции для 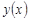справедливо разложение в ряд типа (2.24), т.е.:

(2.25)

то принято говорить, что функция представима своим интерполяционным рядом Лагранжа.

Возьмем в качестве функцию:

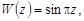тогда

(2.26)

Таким образом, разложение в гармонический ряд (2.13) – это также интерполяционный ряд Лагранжа, только с другой функцией .

Глава 3. Пропускная способность
канала с белым гауссовским шумом

Сформулируем окончательно теорему об отсчетах так, как она была сформулирована В.А. Котельниковым в 1933 году. Речь идет о функциях со спектром, сосредоточенным на отрезке 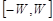и формуле их представления в виде гармонического ряда вида:

(3.1)

Эта формула немедленно получается из формулы (2.19) предыдущей главы, если принять за единицу измерения времени величину 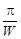секунд. Формулировка В.А. Котельникова такова: «количество информации, требуемой для записи сигнала со спектром на на временном интервале длины Т при больших Т, пропорционально ».

Можно заметить, что теорема Котельникова в ее исходной формулировке не является строгим математическим результатом: ей можно придать несколько разных смыслов. По-видимому, основные смыслы такие: функциональный, вероятностный и фрактальный (геометрический).

Развитие в направлении теории функций привело к появлению нового раздела математики – гармонического анализа и в конечном счете – абстрактного гармонического анализа операторов. Основоположники – это Пэли и Винер.

Вероятностная сторона спектрального анализа – это фундаментальные работы Колмогорова.

Фрактальный подход – восходит к идеям самого Шеннона и развивается, прежде всего, школой Колмогорова.

Собственно к теории сигналов и информатике в первую очередь имеет отношение фрактальный подход. Этот подход стартовал с работы Шеннона, в которой дана верхняя оценка пропускной способности канала с белым гауссовским шумом. Остановимся на этом более подробно.

Рассмотрим теперь более подробно свойства семейства функций:

(3.2)

Функции семейства (3.2) принадлежат гильбертову пространству . В самом деле:

, ,

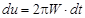где мы воспользовались хорошо известным из математического анализа интегралом:

Тем самым мы показали, что норма всех функций из семейства (3.2) равна:

(3.3)

и не зависит от k.

Кроме того, можно также показать, что функции из семейства (2.13) ортогональны в , т.е.:

(3.4)

при .

Иными словами, значение можно использовать, как координаты функции в бесконечномерном пространстве . Норме функции в квадрате по смыслу физических величин соответствует величина работы по передаче сигнала по каналу:

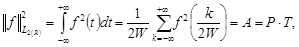(3.5)

где Р – средняя мощность сигнала, а Т – длительность его передачи.

Отсюда:

. (3.6)

Если рассматривать сигналы, мощность которых ограничена величиной Р, то им соответствуют точки внутри сферы радиуса:

Допустим теперь, что помеха, т.е. шум, (i) имеет геометрическую структуру сигнала, т.е. это тоже функция из . Кроме того, будем считать, что (ii) каждая координата этой помехи – независимая случайная величина с гауссовским законом распределения и дисперсией 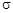– это определение белого шума. Тогда вероятность смещения сигнала на 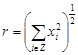равна:

В вышеуказанной формуле .

Иными словами, действие помехи с дисперсией σ соответствует передаче сигнала с мощностью .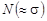

Допустим теперь, что у нас есть система кодировки рассчитанная на исправление ошибок, связанных с белым шумом мощности N. Это означает, что сигнал, попавший в шарик с радиусом , будет идентифицироваться с центром этого шарика, т.е. ошибка будет исправлена. Сделаем верхнюю оценку пропускной способности такого канала «с исправлением» ошибок.

Шар максимального радиуса, в котором содержатся сигналы с мощностью Р и мощностью шума при длительности Т равен:

. (3.7)

Напомним, что объем n-мерной сферы радиуса r равен:

. (3.8)

В силу асимптотической формулы Стирлинга, при больших n имеем:

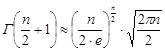, (3.9)

поэтому:

. (3.10)

Объем маленького шарика соответствующего мощности шума:

. (3.11)

Количество различимых сигналов найдем как отношение :

(3.12)

Поэтому верхняя оценка пропускной способности в рассматриваемом случае равна:

(3.13)

Учтем теперь, что n – это размерность пространства в случае ширины полосы W, т.е. , поэтому из (3.13) имеем:

. (3.14)

здесь P – мощность сигнала, N – мощность шума.

Клод Шеннон в своей работе доказывает гораздо более сильный результат и, главное, неожиданный: он показывает, что оценка (3.14) точна! Т.е. неравенство не строгое:

(3.15)

Он конструктивно указывает код, при котором в этом неравенстве достигается равенство:

Теорема (Шеннон). Пусть P – средняя мощность передатчика и пусть помеха есть белый шум с мощностью N в полосе частот W. Применяя достаточно сложную систему кодирования можно передавать двоичные цифры со скоростью:

(3.16)

со сколь угодно малой частотой ошибок. Никакой метод кодирования не допускает передачи с большей скоростью, при произвольно малой частоте ошибок.

Приведенные выше рассуждения доказывают лишь последнее предположение теоремы Шеннона.

Рассмотрим теперь первую часть этой теоремы. Для доказательства первой части теоремы можно, например, явно представить вариант кодирования, который обеспечивает передачу, со скоростью равной бит/сек, при частоте ошибок меньшей, наперед заданного числа . Шеннон предъявляет такую систему: длинная последовательность из m нулей и единиц принимается передатчиком. Всего таких последовательностей штук и каждой из них соответствует специальная функция сигнала длительностью T. Когда данная последовательность заканчивается, передатчик посылает соответствующий сигнал об окончании последовательности.

Приемник принимает искаженный сигнал, сравнивая его с каждым из 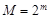возможных сигналов (верных) и выбирает наиболее близкий по среднеквадратическому критерию.

Если случайно вбросить М штук точек в многомерный шар, то эти точки распределятся равномерно по всему объему, но так как объем сосредоточен возле поверхности, то все М точек можно считать распределенными равномерно по поверхности сферы. Шеннон показывает, что это и есть требуемый вариант кодирования.

В самом деле, пусть точка В – это принятый сигнал, т.е. уже искаженный.

Тогда, если передаваемый сигнал лежит в «чечевицеобразной» или линзообразной области заштрихованной на рис. 3, то переданный сигнал будет идентифицирован как правильный.

Рис. 3. Идентификация сигнала в канале с белым шумом

Таким образом, в этой линзообразной области должна лежать ровно одна точка кода. В этом случае ошибки происходить не будет. Вся линзообразная область полностью содержится в шаре с диаметром . Предполагая, что точки передаваемых сигналов случайно распределены на сфере с радиусов , получим, что вероятность любой из них попасть в заштрихованный объем равна:

. (3.17)

Найдем : Рассмотрим треугольник ОАВ, его высота . Заметим, что , т.е. прямо действительно , – это главный момент в доказательстве!

Поэтому

(3.18)

В силу теоремы об отсчётах размерность пространства равна , поэтому из (3.17) получим:

(3.19)

Вероятность того, что все остальные M–1 точки находятся вне этого объема, равна:

(3.20)

Пусть ошибка приема сигнала равна ε, тогда нам нужно добиться выполнения неравенства:

(3.21)

т.е.

(3.22)

Так как M очень велико, то и из (3.22) следует что: .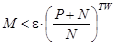

Откуда пропускная способность С такова:

(3.23)

Если ε – фиксировано, то, делая длительность передачи достаточно большой, т.е. устремим , получим, что , т.е. стремится к максимальному теоретическому пределу, чем доказана первая часть теоремы Шеннона.

В качестве интересной задачи можно предложить посчитать объем многомерной линзы на рис. 1.

Глава 4. Числа Фибоначчи.
Пропускная способность алгоритма

Леонардо Фибоначчи в 1202 г. поставил следующую задачу:

Найти все пары чисел, для которых алгоритм Эвклида определения наибольшего общего делителя имеет максимальную длину?

Его решение следующее:

Пусть исходная пара чисел и ( ), тогда имеется следующая система:

……………….
………………. *
……………….

Понятно, что наиболее длинный процесс * появляется в том случае, когда все равны 1, так как при этом из вычитается наименьшее количество :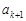

Поэтому сразу можно требовать, чтобы все =1. Понятно также, что процесс * более длинный, когда числа и взаимно просты, т.е. НОД . Таким образом, положим, что . Теперь вся последовательность восстанавливается однозначно:

2 и т.д.

……………….
………………. *
……………….

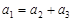
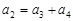
или же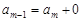

т.е.

Удобно сделать переобозначения нумерации:

Это и есть последовательность, которую обнаружил Фибоначчи:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и т.д.

При делении любой пары идущих подряд чисел из этой последовательности, мы получим все остальные (меньшие) числа в виде остатков, при этом все будут равны 1. Например:

8=5*1+3

5=3*1+2

3=2*1+1

2=1*1+1

1=1*1+0 – здесь искусственно введены только последние два шага алгоритма. На самом деле обычный алгоритм Эвклида занимает на 1 шаг меньше.

Л. Фибоначчи заметил также, что предел:

равен золотому сечению =

Это легко установить, рассматривая определяющее соотношение:

отсюда:

Предполагая, что предел существует, получим:

На самом деле «золотое сечение» играет здесь значительно большую роль.

Нам хотелось бы получить явное выражение для чисел Фибоначчи как функцию n. Рекуррентное соотношение немедленно приводит к такому уравнению в конечных разностях:

С начальными данными:

Что позволяет полностью решить задачу. В самом деле характеристическое уравнение имеет вид:

Отсюда:

Общее решение уравнения имеет вид:

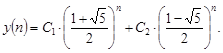
Подставляя и , получим уравнение для определения и :

Отсюда:

Наконец:

Поэтому интересующее нас представление чисел Фибоначчи имеет вид:

Таким образом мы установили, что общий член последовательности Фибоначчи имеет такой вид:

Вы уже заметили всю необычность ситуации: числа Фибоначчи – целые, а выражение, которое мы только что получили, содержит иррациональности, в нём как-то трудно усмотреть целые числа.

Однако, факт остаётся фактом – это действительно числа Фибоначчи. Согласитесь, что угадать такую закономерность, аналогично тому, как это делается с последовательностью квадратов, кубов или членов арифметической прогрессии, довольно трудно. Такова сила метода уравнений в конечных разностях. Заметим ещё вот что, модуль второго корня характеристического уравнения меньше единицы. Поэтому второе слагаемое в квадратной скобке с ростом номера стремится к нулю. А первое слагаемое определяет геометрическую прогрессию. Таким образом, мы можем сделать вывод, что числа Фибоначчи при больших n ведут себя «почти» как геометрическая прогрессия, но не точно, а с точностью до округления до ближайшего целого.

Итак, при больших n величина пренебрежимо мала. Это обстоятельство позволяет оценить число шагов алгоритма Эвклида для определения наибольшего общего делителя из соотношения:

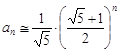Отсюда:

поэтому:

Таким образом, имеет место такая оценка (для достаточно больших чисел).

где р – число знаков в десятичной записи

В теории пропускной способности имеем:

– пропускная способность алгоритма Эвклида.

Таким образом, мы можем естественно определить пропускную способность произвольного алгоритма как отношение:

n – имеет смысл времени (дискретного) в любой логической схеме.

Вы также легко догадаетесь, что последовательность может быть продолжена влево, и соответствующий предел равен числу , сопряжённому к золотому сечению.

Двусторонняя последовательность Фибоначчи:

…34, -21, 13, -8, 5, -3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…

Существенно для нас заметить одну важную особенность. Корни характеристического уравнения оказались иррациональными числами, а решение принимает целочисленные значения в целых точках. Именно такая ситуация складывается и в нашей исходной задаче с уравнением для пропускной способности канала без шума.

Так что пример с числами Фибоначчи не только представляет пропускную способность алгоритма Эвклида, но и вообще иллюстрирует общую закономерность в расчётах пропускной способности. Наконец, возвращаясь к нашим первым лекциям, Вы можете заметить, что алгоритм Эвклида является более лучшим каналом, нежели телеграф. ( Вопрос к зачёту: почему?)

Глава 5. Задача А.А. Маркова

В книге «Исчисление конечных разностей» Марков формулирует и решает задачу, представляющую значительный интерес для сглаживания временных рядов методом скользящего суммирования. И до сегодняшнего времени этот метод является единственным, с точностью до некоторых «вариаций» на тему, методом обработки дискретных числовых данных с дискретной, равномерной областью определения. Предполагается, что временной ряд содержит некоторые случайные наслоения высокого порядка, некоторую «шелуху», которая накладываясь на объективную картину, мешает понять присущие рассматриваемому процессу внутренние закономерности. Представьте себе, например, что Вы анализируете базу данных регистратуры какой-нибудь районной поликлиники. Вы рассматриваете количество обращений с желудочно-кишечными заболеваниями и сталкиваетесь с тем, что абсолютный максимум обращений приходится на некоторый день января. Можно ли отсюда сделать вывод, что январь наиболее опасен с точки зрения желудочно-кишечных заболеваний? Конечно, нет. Просто в этот день несколько семей собрались отметить день рождения, открыли банку с грибами, а они оказались «не правильными». В результате пятнадцать человек одновременно обратились в эту поликлинику, что и потянуло кривую обращаемости вверх, до абсолютного максимума. Здесь мы сталкиваемся со случайностью более высокого порядка. На самом деле наиболее опасным временем с точки зрения желудочно-кишечных заболеваний является начало июня и начало августа. Это время сильной жары, не мытых рук, появления на рынках клубники, черешни, а во втором случае арбузов и дынь. А банка с грибами только затуманивает эту картину. Метод скользящего суммирования направлен на то, чтобы очистить временной ряд от этих наслоений. Собственно сам метод устроен гениально просто: фиксируется некоторый интервал суммирования, например, по 2, 5 или даже 10 значений. Рассматривается первых k значений временного ряда, берётся их среднее арифметическое и устанавливается соответствующая точка. Затем интервал суммирования сдвигается на одну позицию вправо, оправдывая тем самым название метода, и делается тоже самое. И так – до конца временного ряда. Такая процедура проделывается с получившимся рядом несколько, а возможно и много, раз. В результате углы между последовательными отрезками ломаной становятся менее острыми. Это принято интерпретировать, как сглаживание кривой. С точки зрения классического математического анализа, кривая не стала более гладкой, она как была кусочно-линейной функцией, так и осталась ею. Но теперь на ней нет ярко выраженных пиков: мы тем самым лишили себя испорченных грибочков. Сейчас не представляется возможным установить авторство этого алгоритма, но есть все основания считать, что он существовал до сотворения мира. Это та самая гениальная простота, которая не оставляет сомнений в авторстве. Перейдём теперь собственно к модели Маркова. Пусть дано 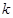чисел . Формируется бесконечная последовательность из скользящих арифметических средних:

и т.д.

Требуется найти предельное значение , и доказать, что оно единственно, т.е., что есть единственная предельная точка.

Среднее арифметическое удовлетворяет неравенствам

поэтому вся последовательность ограничена и, в силу теоремы Кантора, имеет по крайней мере одну предельную точку.

Введем функцию , такую, что она удовлетворяет линейному разностному уравнению:

Соответствующее характеристическое уравнение имеет вид:

Понятно, что – корень этого уравнения. Легко показать, что все корни , в самом деле:

отсюда:

если , то сумма справа больше k , т.к. содержит ровно k слагаемых. Можно заметить, что полученный полином является производной полинома:

Хорошо известно, что 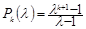и, следовательно, корни однократны и лежат в вершинах правильного k -угольника вписанного в единичную окружность, за исключением вершины .

В силу теоремы Лукаса, все корни производной лежат в выпуклом многоугольнике M , т.е. внутри единичной окружности. Поэтому все остальные 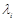в действительности удовлетворяют более сильному неравенству (строго!!!).

Несколько слов о теореме Лукаса ( Lucas , 1874 г.) – если все корни полинома принадлежат какому-либо выпуклому многоугольнику, то и все корни производной этого полинома также принадлежат этому многоугольнику. Аналогично для круга и отрезка. Эти теоремы обобщают теорему Ролля на случай функций комплексного переменного.

Вообще говоря, теорема Ролля для функций комплексного переменного места не имеет. В самом деле, аналитическая функция: имеет нули, например, в точках и , но ее производная вообще не обращается в нуль, т.е. не имеет нулей, однако для полиномов обобщение теоремы Ролля, как, оказалось, имеют место. Это и есть теорема Лукаса (со всеми ее вариантами).

Доказательство указанной теоремы и вариации на эту тему можно найти в книге: M . Marden , The geometry of the zeros of a polynomial in a complex variables , № 3, AMS . Providence , 1966, Chapter II. The critical points of a polynomial and some of their generalizations, p. 14-31.

Результаты Лукаса, по видимому, были хорошо известны АА Маркову в связи с их широким обсуждением в математической печати.

Для вещественных полиномов полезна также следующая теорема о локализации комплексных корней производной.

Теорема Йенсена. Каждый не вещественный корень производной вещественного полинома принадлежит, по крайней мере, одному кругу Йенсена.

Круг Йенсена соответствующий паре комплексно сопряженных корней полинома строится по ним, как по диаметру.

Задача. Компьютерно построить корни уравнений

для достаточно больших k .

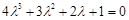
Для нас важно, что внутри окружности находится k–1 корень, т.е. собственно на окружности лежит ровно один корень .

Общее решение в этом случае выглядит так:

Искомое решение равно:

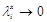, т.к. все , то при .

где – верхняя строка матрицы W обратной к матрице Вандермонда, т.е.:

Понятно, что, сделав сдвиг на одну позицию, мы не изменим значение предельной точки, поэтому:

Приравнивая коэффициенты при 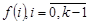получим k уравнений:

Поэтому:

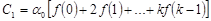Остается найти , но эта постоянная вообще абсолютная, т.е. не от чего не зависит и может быть найдена, например, так: полагая все , получим , т.е. , тогда:

отсюда:

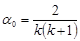Таким образом, окончательный ответ такой:

Например: , имеем:

Для тех, кто будет читать первое издание «Исчисления конечных разностей» А. О. Гельфонда, обратите внимание, что на с. 131 допущена опечатка, которая в несколько изменённом виде перекочевала во все последующие переиздания, следует читать

Далее рассматриваем скользящее усреднение с произвольными положительными весовыми коэффициентами. Докажем, что справедлива следующая предварительная Лемма.

Лемма. Пусть все весовые коэффициенты положительны , тогда все корни характеристического полинома, за исключением 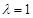, расположены строго внутри единичного круга.

Доказательство. Воспользуемся тождеством:

(5.1)

Таким образом, нас интересуют корни полинома в квадратных скобках (5.1). Обозначим через и соответственно минимум, и максимум отношений последовательных коэффициентов этого полинома:

(5.2)

(5.3)

Тогда, в силу теоремы Гурвица (см., например, (5) Г. Полиа, Г. Сегё, Задачи и теоремы из анализа, т. 1, М., Наука, 1978, с. 144, 208, задача 23). Корни указанного полинома расположены в кольце:

(5.4)

Так, как все , то выполнено строгое неравенство , и Лемма доказана.

Теорема. Пусть все весовые коэффициенты положительны , тогда предел рекуррентной последовательности существует и выполнено соотношение:

(5.5)

Доказательство. Решая уравнение в конечных разностях, получим:

(5.6)

здесь х принадлежит множеству натуральных чисел, – корни многочлена из тождества (5.1). В силу предыдущей Леммы модули этих корней меньше 1. Поэтому существует предел . Постоянная находится как решение системы линейных уравнений с правыми частями и, следовательно, является линейной комбинацией начальных данных, т.е.:

(5.7)

Для определения коэффициентов линейной комбинации мы, не решая соответствующую систему уравнений, воспользуемся следующим соображением: (см. (6) Марков А.А. Исчисление конечных разностей) так как рекуррентный процесс сходится, то его предел не зависит от выбора начального шага, в частности:

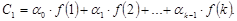(5.8)

Из (5.7) и (5.8), с учетом рекуррентного соотношения, получим:

(5.9)

Так как начальные данные произвольны, то для выполнения (5.9) необходимо равенство коэффициентов при одинаковых 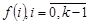. Приравнивая соответствующие коэффициенты, находим:

Действуя аналогично, получим далее:

(5.10)

Таким образом, мы нашли с точностью до мультипликативной постоянной :

(5.11)

Для определения положим, что все начальные данные одинаковы , тогда рекуррентная последовательность имеет вид: , поэтому 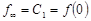. Отсюда получим уравнение для :

(5.12)

Из (5.12) следует, что:

Подставляя найденное в (5.11) немедленно получим соотношение (5.5) и теорема полностью доказана.

Рассмотрим теперь арифметические прогрессии вида:

где – фиксированное неотрицательное число. И положим, что весовые коэффициенты равны последовательным членам указанных прогрессий так, что:

…, …

Понятно, что все и, следовательно, мы находимся в условиях применимости доказанной теоремы. Тогда коэффициенты при начальных данных в числителе соотношения (5.5) равны последовательным частным суммам указанных прогрессий:

(5.13)

Для дальнейшего удобно положить , тогда из (5.13) получим:

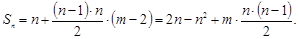(5.14)

Таким образом, соотношение (5.5) принимает вид:

(5.15)

где – последовательность m -угольных чисел (см., например, [7] Эдвардс), определяемых соотношениями (5.14).

Обозначим через сумму первых k m -угольных чисел:

(5.16)

Тогда удовлетворяют следующему уравнению в конечных разностях:

(5.17)

Частное решение неоднородного уравнения (5.17) будем искать в виде кубического многочлена:

(5.18)

Подставляя (5.18) в (5.17) и приравнивая коэффициенты при одинаковых степенях k , получим:

(5.19)

Из того, что немедленно следует, что , поэтому для имеет место, следующее соотношение:

(5.20)

Таким образом, соотношение (5.15) можно представить в виде:

где коэффициенты при начальных данных равны:

, (5.21)

где

Замечание 1. Числа принято называть пирамидальными, однако авторы не нашли печатные источники, на которые можно было бы сделать аккуратную ссылку в смысле определения и формулы, поэтому мы приводим соотношение (5.20) с доказательством в удобной для нас форме.

Замечание 2. При из соотношения (5.21) получим:

что соответствует известному решению задачи А.А. Маркова ([6] Исчисление конечных разностей).

Отметим также, что имеют место следующие предельные соотношения:

откуда Таким образом, в пределе рекуррентный процесс полностью «забывает» первое начальное данное.

Пример. Рассмотрим семейство всех арифметических прогрессий, содержащихся в натуральном ряде и начинающихся с числа 1:

1, 1, 1, …
1, 2, 3, …                             (собственно натуральный ряд)
1, 3, 5, … (ряд нечетных чисел, решение сравнения х≡1(mod 2))
1, 4, 7, …                            (решение сравнения х≡1(mod 3))
1, 5, 9, …                            (решение сравнения х≡1(mod 4))
и т.д.

Все эти прогрессии равноправны, в том смысле, что любая из них может быть использована в качестве весовых коэффициентов p₁, p₂, p₃, … в скользящем соотношении:

Решая задачу Маркова для каждой из этих последовательностей, получим следующие коэффициенты в числителях (5.5):

1, 2, 3, 4, 5, 6, 7, 8, … ,

1, 3, 6, 10, 15, 21, 28, 36, … ,

1, 4, 9, 16, 25, 36, 49, 64, … ,

1, 5, 12, 22, 35, 51, 70, 92, … ,

1, 6, 15, 28, 45, 66, 91, 120, … ,

1, 7, 18, 34, 55, 81, 112, 148, … ,

1, 8, 21, 40, 65, 96, 133, 176, … ,

и т.д.

Из определения m -угольных чисел (см. например, [Эдвардс (1980)]) немедленно следует, что в этих строчках, начиная со второй, расположены треугольные числа, четырехугольные числа, пентагональные числа и т.д.

Отметим, что первая таблица не представляет особенного интереса как средство статистической обработки временных рядов. По существу эта таблица содержит две принципиально различные строчки: первую и вторую. Коэффициенты из первой строки обеспечивают равномерное влияние всех элементов временного ряда, коэффициенты из второй строки позволяют равномерно усиливать влияние элементов ряда.

Вторая таблица содержит m -угольные числа, и лишена в этом смысле, указанного недостатка. Каждая строка этой таблицы позволяет неравномерно менять влияние элементов ряда так, что более ранние элементы имеют относительно меньшее влияние, нежели более поздние, причем степень этой неравномерности регулируется целочисленным параметром m (m≥2). Таким образом, можно разработать инструмент обработки временного ряда, обладающий бесконечным репертуаром внутренних состояний.

Проиллюстрируем эффективность данного метода предварительной обработки временных рядов на конкретных исторических данных: рассмотрим валютный курс USD/CHF за период с июня 1972 г. по декабрь 2003 г. (источник котировок EuroClub http://www.fxeuroclub.ru и Сембанк http://www.sembank.ru).

Интервал сглаживания выбран равным 7 дням. Исследование предлагаемого взвешенного скользящего усреднения включало следующие этапы.

Усреднение без весов (простая средняя). Поскольку интервал сглаживания ограничен несколькими днями, то предлагается данную процедуру повторять (для иллюстрации производимого эффекта это было проделано 100 раз, хотя для практических целей можно ограничиться меньшим числом повторений) для качественной «очистки» исходного ряда от случайных флуктуаций. Заметим, что использование одной процедуры с большим интервалом и нескольких повторных процедур с малым интервалом усреднения приводят к разным результатам. Ограничивая интервал сглаживания несколькими уровнями (в нашем случае 7), при многократном повторении получаем гладкий тренд, не теряя при этом амплитуды основной динамики, в отличие от однократного усреднения по большому числу уровней.

На втором этапе производилось взвешенное усреднение на интервале такого же размера (7 дней). Процедура также повторялась 100 раз. Такое большое число повторений выбрано для визуального сравнения результатов сглаживания двумя способами: без весов и с весами. С каждым новым усреднением получаем новую сглаженную кривую и, изобразив все эти кривые вместе, формируем «полосы». Сравнивая ширину этих полос, можно оценить разницу между двумя вариантами сглаживания.

Таким образом, сначала был использован метод простой скользящей средней с многократным повторением усреднения. На рис.4 представлен фрагмент результата процедур последовательного сглаживания (100 раз) с помощью среднеарифметического сглаженного значения, присваиваемого крайнему правому уровню интервала сглаживания.

Основным недостатком данной процедуры является сильное смещение вправо расчетных сглаженных значений относительно исходных данных и незначительное уменьшение амплитуды колебаний.

Рис. 4. Результаты 100 раз произведенного сглаживания USD/CHF по методу простой скользящей средней

На втором этапе для взвешенного скользящего усреднения был выбран набор удельных коэффициентов, соответствующих нижней строке таблицы с многоугольными числами. Процедура сглаживания временного ряда последовательно повторялась (100 раз) для максимальной очистки исходного временного ряда от незначительных возмущений. Введение весовых коэффициентов позволило придать больший удельный вес уровням, ближним к тому, для которого вычислялось сглаженное значение, и меньшие веса уровням, по мере удаления их от сглаживаемого.

На рис. 5 представлены результаты взвешенного скользящего усреднения:

Приведенные на рис. 4 и 5графики сглаживания подтверждают пользу предлагаемого метода расчета весовых коэффициентов, который позволяет приблизить сглаженные значения к исходным данным. Это определяется разницей в ширине полос на рисунках, т.е. не уменьшая полезность всей процедуры, позволяющей исключить из исходного ряда незначительные колебания, не потеряв периодов роста и спада, уменьшаем расхождение между исходными и выровненными данными.

Рис. 5. Результаты 100 раз произведенного сглаживания USD/CHF по методу взвешенной скользящей средней

Рассмотрим несколько естественных обобщений метода Маркова. Оказывается, что приведенное выше решение даёт возможность решить аналогичные задачи для геометрического и гармонического средних.

Задача 1. Рассмотрим рекуррентный процесс для среднего геометрического:

и т.д

Найти .

Здесь решение связано с нелинейным уравнением:

Ясно, что непосредственно использовать метод линейных уравнений в конечных разностях не удаётся. Однако, если подсчитать степени, то мы сразу придём к уже полученным соотношениям в задаче Маркова. В самом деле:

Числители в и .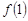

Таким образом, решение имеет вид

При , , получим

, .

Отсюда ; .

Далее

Таким образом, ответ имеет вид

Задача 2: Для среднего гармонического.

Верно ли это?

Решение задачи 2:

Здесь та же последовательность, что и в задаче 1, т.е. получим:

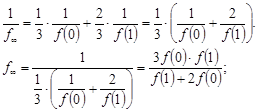
Следствие.

Имеют место неравенства для .

, причем равенства достигаются только при .

Задача 3. Получить обобщение задач 1 и 2 на случай n переменных:

– задано k чисел, считается корень k -ой степени.

Верно ли что предел такой?

Задача 4.

Получить обобщение для k -среднего гармонического.

Покажите, что справедливо соотношение:

Теорема. (рекуррентные средние). Пусть , тогда имеют место следующие неравенства:

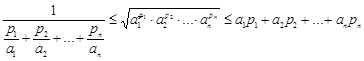, равенства возможны только при .

Пример 1.

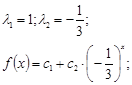
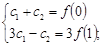
Пример 2.

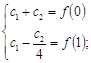
Что получается в общем виде?

если , т.е. все корни, очевидно, меньше 1. (Установить, используя доказанную ранее лемму!).

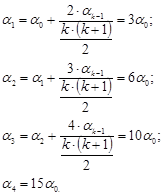
Найдем теперь пусть все .

, т.е. все члены последовательности одинаковы и следовательно

отсюда :

Решение ищем в виде кубического полинома:

При , получим:

Иными словами, применяя рекуррентно метод Маркова, мы получим из последовательности единиц таблицу, известную Вам, как треугольник Паскаля (только он будет, развёрнут так, чтобы представлять таблицу). Это приложения в области анализа. Однако не менее интересны и другие приложения.

Дадим определение, которое часто используется в математической статистике при обработке временных рядов:

Начётным рядом называется ряд из последовательных частных сумм заданной последовательности чисел.

Например:

1, 1, 1, 1, 1, 1, 1,…

1, 2, 3, 4, 5, 6, 7,…

Понятно, что метод Маркова представляет формальную модель генерирования начётного ряда по любой заданной последовательности чисел, разумеется, при выполнении условий леммы о корнях полинома. Все последовательности, которые мы будем рассматривать дальше, состоят из положительных чисел, поэтому выполнены условия леммы и наши построения вполне корректны.

Рассмотрим способ генерирования последовательности чисел, в которой, каждый член умножен на некоторую степень своего номера. Здесь, кроме начётного ряда используется метод решета, то есть зачёркивания некоторых членов последовательности, наподобие решета Эратосфена, для определения простых чисел. Вы, как постоянные участники олимпиад, знаете, о чём идёт речь, поэтому напоминать не буду. Введём такие обозначения

– обозначает операцию зачёркивания каждого n -го члена последовательности. Я, конечно, использую не собственно зачёркивание, а просто стираю с доски – попробуйте эту операцию смоделировать арифметически!

Например:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10

= 1, 2, 4, 5, 7, 8, 10

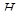– обозначает операцию построения начётного ряда.

Например:

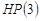= 1, 3, 7, 12, 19, 25, 35

Возьмём теперь любую арифметическую прогрессию, которая начинается с единицы и имеет неотрицательную разность. Применим к ней, например, следующую суперпозицию операций :

1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34

Получим такую последовательность

1, 5, 15, 28, 47, 69, 97, 129

К этой последовательности снова применим операцию с уменьшением показателя зачёркивания на единицу Н P (2), получим такую последовательность:

1, 16, 63, 160.

Заметим теперь, что полученная последовательность состоит из чисел, равных произведению члена исходной прогрессии на его номер в квадрате: 1=1*1*1, 16=4*2*2, 63=7*3*3, 160= 10*4*4 и т.д.

Оказывается, что если начинать применять описанные выше операции с показателя n , то есть

то мы получили бы произведения членов прогрессии на их номера в степени . Наиболее красивый результат получится, если в качестве исходной прогрессии взять натуральный ряд. В самом деле, в такой прогрессии как натуральный ряд каждый член прогрессии равен своему номеру, поэтому в результате указанных действий, мы получим последовательность, состоящую из степеней натуральных чисел. Этот последний случай обнаружил впервые немецкий математик А. Мейсснер: A . Moessner , Eine Bemerkung uber die Potenzen der naturlichen Zahlen , в 1951 году. Вы можете прочитать об этом также в замечательной книжке С. П. Боброва, Архимедово лето, том 1. 1959г. с. 292–293. Этот пример приведен в книге Д. Кнут и др., Конкретная математика, в качестве упражнения на с. 416–417. Мы приводим здесь некоторое обобщение в терминах любой арифметической прогрессии, а не только натурального ряда. Но ключевым моментом здесь является результат Мейсснера. Частным случаем этой теоремы является, например, хорошо известный факт, что начётные суммы ряда нечётных чисел равны квадратам натуральных чисел. Оказалось, что факт известный на протяжении нескольких тысячелетий, входит в некоторую общую схему, которую обнаружили совсем недавно. Более того, можно заметить, что количество статей, связанных с теоремой Мейсснера, с каждым годом возрастает.

Заметим далее, что до сих пор мы смотрели на последовательность единиц как на арифметическую прогрессию с разностью равной нулю. Результат Мейсснера позволяет увидеть в этом ряде также нулевые степени последовательности натуральных чисел.

Задача. Показать, что если образовать начётный ряд второго порядка (суммы по два элемента) из нечётных чисел, получим ряд квадратов чётных чисел, для начётного ряда третьего порядка, соответственно ряд квадратов чисел, кратных трём, и т.д., для начётного ряда n -го порядка, получим ряд квадратов чисел, кратных n . Рассмотреть возможные обобщения.

Глава 6. Многоугольные числа

Рассматривая обобщение задачи Маркова, мы неожиданно столкнулись с многоугольными числами. Остановимся на этом чуть более подробно.

Многоугольные числа были известны древним египтянам. Они являются основой пифагорейства. В новое время наиболее сильный результат связанный с многоугольными числами известен как «золотая теорема» Ферма:

Любое натуральное число

- либо само является треугольным, либо представимо в виде суммы не более трёх треугольных чисел;

- либо само является четырехугольным, либо представимо в виде суммы не более четырёх четырехугольных чисел;

и т.д.

Частные случаи этой теоремы были доказаны позднее Эйлером и Лежандром. Полное доказательство получил Коши в 1815 году. На самом деле он доказал, что любое натуральное число представимо в виде суммы не более четырёх m-угольных чисел ( m больше или равно 4) и не менее m – 4 единиц. Поэтому теорема Ферма часто формулируется в виде теоремы о четырёх квадратах. Формально это частный случай «золотой теоремы», но это наиболее содержательный частный случай.

Вообще в связи с многоугольными числами не возможно удержаться, чтобы не привести цитату из Литлвуда – это выдающийся английский математик середины ХХ века: «древние греки – не умные школьники и не кандидаты на стипендию за отличные успехи, а это учёные из другого колледжа».

Несколько позднее мы также рассмотрим некоторые свойства таблицы многоугольных чисел.

Получим формулу для n-го m-угольного числа, используя решение уравнения в конечных разностях. Геометрические соображения немедленно приводят к такому соотношению:

(6.1)

Например, при 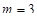: треугольные числа:

m=4: квадраты :

m=5: пентагональные числа :

Рассмотрим теперь задачу в общем случае. Будем искать частное решение в виде:

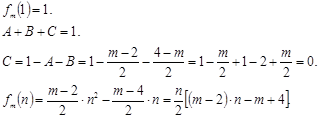
При фиксированном n получаем арифметические прогрессии:

	n =1	n =2	n =3	n =4	n =5	n =6	n =7	n =8
m =2	1	2	3	4	5	6	7	8
m =3	1	3	6	10	15	21	28	36
m =4	1	4	9	16	25	36	49	64
m =5	1	5	12	22	35	51	70	92

m=2: двухугольные числа: это решения разностного уравнения вида:

– это случай А.А. Маркова.

При и меньше формула перестает работать. Под одноугольными числами естественно следует понимать одно число 1.

1, 1, 1, ….

В этом случае:

Если , то

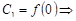
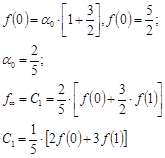
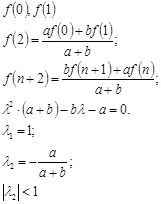
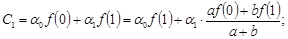
при ;

При

?! – не возможно.

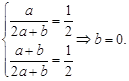
Остальные

При всех одинаковых , получим:

В частности при …… получим:

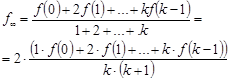
Обозначим через – n-е m-угольное число.

1₁=1; 1₂=1; 1₃=1; …. – 1-угольные числа.

2₁=1; 2₂=2; 2₃=3; … – 2-угольные числа.

3₁=1; 3₂=3; 3₃=6; 3₄=10; … – 3-угольные числа.

4₁=1; 4₂=4; 4₃=9; 4₄=16; … – 4-угольные числа.

5₁=1; 5₂=5; 5₃=12; 5₄=22; … – 5-угольные числа.

Обозначим:

– сумма первых N штук m-угольных чисел.

Тогда для средних геометрических имеем:

Для средних гармонических:

Обобщенные неравенства между средними арифметическими, гармоническими и геометрическими:

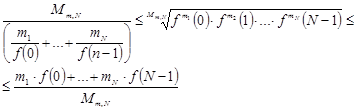
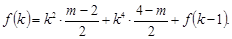
– для любых m ( ).

N+1

– сумма первых N m-угольных чисел ( ).

Для пентагональных чисел:

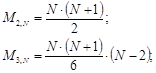
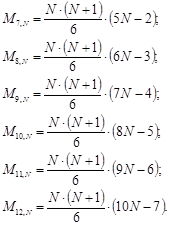
		m=2
		m=3
		m=4
		m=5
		m=6
		m=7
		m=8
		m=9
		m=10
		m=11
		m=12

Если N и N+1 не делится на 3, то и, следовательно,

Здесь несколько выпадают только пентагональные числа: сразу явно сокращается тройка:

Но в целом картина достаточно универсальна (при ).

При , – это сумма N единиц.

Глава 7. Таблица многоугольных чисел. Уравнение Ферма (Пелля).
Непрерывные дроби

Теперь нам хотелось бы изучить информационную состоятельность таблицы многоугольных чисел. Прежде всего, интересно узнать часто ли повторяются числа в различных строчках, да и повторяются ли они вообще.

1. Выясним, попадают ли треугольные числа в четырехугольные. Для этого необходимо решить следующее уравнение в целых числах:

Отсюда :

Выделяя полный квадрат, после некоторых преобразований, получим:

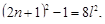
Таким образом, мы приходим к необходимости решить уравнение Ферма:

где D – не равно квадрату целого числа, больше известное как уравнение Пелля. Этим названием, на самом деле, мы обязаны Эйлеру, который ошибочно решил что именно английский математик Пелль был первым кому удалось получить решения такого типа уравнений (см. [18] Неопубликованные материалы Л. Эйлера по теории чисел, СПб.: Наука, 1997, с. 254).

Я сейчас просто покажу, как надо решать полученное выше уравнение. Это будет такой, предварительный алгоритм.

Сначала нам нужно найти разложение в непрерывную дробь. Это делается следующим образом:

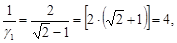
С этого места в дроби начинается повтор.

Общий вид дроби такой:

В нашем случае получим:

Выпишем теперь подходящие дроби, соответствующие нечетным позициям:

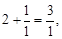отсюда,

т.е. числитель дроби – это x, а знаменатель y – дают решение уравнения Ферма: , .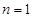

Отсюда , – следующая пара решений:

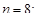
вторая пара решений: 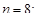т.е. восьмое треугольное число является полным квадратом.

Здесь задача решается совсем просто. Все нечетные подходящие дроби будут давать x и y в уравнении Ферма, при этом так как 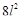– четное число, то 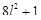– не четное число, поэтому, x должно быть не четным числом, но в нашем случае – любое нечетное число, поэтому все решения подходят.

В других случаях ситуация оказывается значительно сложнее. Мы это увидим позже. А сейчас я приведу обязательный пример одной непрерывной дроби. Это дробь для «золотого сечения» . Мы уже встречались с этим числом при изучении чисел Фибоначчи.

– но это уже повтор, поэтому , и т.д.

Следовательно :

То есть дробь состоит только из одних единиц! Это видимо самая красивая непрерывная дробь известная с древнейших времён. И, конечно, мы ещё раз убеждаемся в некоторой «избранности» золотого сечения. Вот соответствующие подходящие дроби:

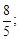
и т.д., таким образом, подходящие дроби – это решение задачи Фибоначчи.

Рассмотрим теперь более сложные ситуации.

2. Попытаемся, вслед за Эйлером, выяснить встречаются ли среди пентагональных чисел полные квадраты, т.е. есть ли не тривиальные совпадения в третьей и четвертой строках нашей таблицы. Задача сводится к такому уравнению в целых числах:

откуда :

выделяя полный квадрат, получим:

отсюда :

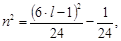
Наконец мы снова приходим к уравнению Пелля :

Действуя как ранее, получим:

Подходящие дроби:

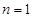– это тривиальное решение.

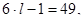
– не целое число,

Здесь мы впервые сталкиваемся с основной проблемой этих задач: числитель и знаменатель подходящей дроби должны попасть в некоторые арифметические прогрессии. В данном случае число 49 не попало в арифметическую прогрессию: и найденное решение не подходит.

Посмотрим, что даст следующее приближение:

Таким образом, первое не тривиальное решение таково:

т.е. 81-е пентагональное число является полным квадратом, это .

Задача 1. Попытайтесь найти общее решение задачи и тем самым показать, что подходящих чисел бесконечно много.

Указание 1. Задача сложная. Если долго не получается ее решить, то можно подсмотреть решение в «Универсальной арифметике» Эйлера, п.88.

Задача 2. Найти первое не тривиальное совпадение четырехугольных и шестиугольных чисел.

Указание 2. Свести задачу к решению уравнения и показать, что

Более сложный тип уравнений похожих на уравнение Пелля также появляется при изучении полученной нами таблицы.

3. Совпадение четырехугольных и семиугольных чисел.

Рассуждая, как и ранее получим такое уравнение:

отсюда после некоторых преобразований:

придем к такому уравнению:

Нам известно очевидное решение:

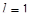
Итак, мы получили уравнение вида:

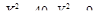
Это не уравнение Пелля, однако, есть потрясающая по простоте идея его решения: может быть, решения этого уравнения есть некоторые линейные комбинации решений соответствующего уравнения Пелля:

Покажем, что это действительно путь решения. В самом деле, будем искать решения X и Y в виде:

где U и V – решения уравнения Пелля с неоднородностью равной 1. Подставляя в уравнение такую форму решений, получим:

отсюда, с учетом того, что , получим:

Отсюда :

Одно решение нам известно

Далее:

Кроме того:

Таким образом, мы действительно получили решение:

Оказывается, что так можно решать любое уравнение вида:

если известно хотя бы одно решение, т.е. тогда можно найти все решения. Это как раз наш случай.

Теперь остается найти U и V – решение уравнения Пелля:

Здесь будем действовать так, как мы делали раньше. Сначала находим непрерывную дробь для :

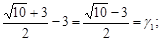
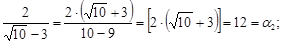
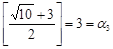
, далее идет повтор.

Таким образом, получим такую непрерывную дробь:

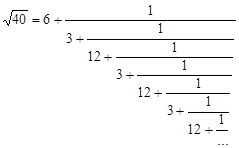
Рассматривая подходящие дроби можно найти:

Откуда получим первое нетривиальное совпадение:

Такие задачи далее уже трудно решать вручную и пора переходить к компьютерным решениям.

При определении подходящих дробей для , которые дают решения уравнения Пелля, необходимо использовать следующую теорему (см. А.З. Вальфиш, Уравнение Пелля, Из-во АН Грузинской ССР, Тбилиси, 1952, с. 74).

Теорема. Пусть 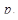является числителем, а – знаменателем i-ой подходящей дроби числа . Пусть далее – есть i-й остаток числа , а N – наименьшее положительное целое, для которого имеет место

Тогда положительные решения уравнения Пелля x и y

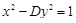
есть числа:

для четного N,

для нечетного N.

В частности, наименьшее положительное решение уравнения Пелля есть:

для четного N,

для нечетного N.

В рассмотренном выше случае, понятно, что N=2. И первое нетривиальное решение соответствует .

Полное доступное изложение теории уравнений Пелля и близких к ним можно найти в прекрасном учебнике Диксона (Л.Е. Диксон, Введение в теорию чисел, Из-во АН ГССР, Тбилиси, 1941 г., 407 с.). Однако эта книга давно стала библиографической редкостью и вместо нее можно рекомендовать книгу переводчика и человека, решившего все задачи из учебника Диксона. Это указанная выше книга Вальфиша.

Сформулируем теперь две интересные исследовательские задачи.

Задача 1. Опишите все случаи, когда отличитель уравнения (отличителем называется число D) является полным квадратом. Решите задачу в этих случаях. Покажите, например, что среди десятиугольных чисел нет полных квадратов, за исключением, конечно, тривиальной 1.

Указание. Задача простая, но требует некоторой аккуратности в длительных выкладках.

Задача 2. Выясните есть ли среди шестиугольных чисел нетривиальные пентагональные числа.

Покажите, что задача сводится к решению уравнения:

далее используйте компьютер. Непрерывная дробь для у нас получена ранее.

Указание. Задача сложная. Посмотреть решение негде!

Отметим, наконец, что изучение неопределенных уравнений второй степени занимает математиков не одну тысячу лет. Известно, что Архимед предложил Эратосфену текстовую задачу, которая сводилась к решению такого уравнения:

Наименьшее решение было найдено в 1880 году:

y=50 549 485 234 033 074 477 819 735 840 408 986 340.

И есть все основания считать, что античные математики умели решать такие задачи. Скорее всего их научили этому египтяне. Попробуйте и Вы решить эту задачу на компьютере.

Вообще, та свобода, в хорошем смысле, конечно, с которой египтяне, а затем и эллины, обращались с числами была утеряна на несколько столетий. Скорее всего, что древние египтяне не заработали чисел. Они получили их как дар. Возможно, это было приложение к чему-то значительно большему. А возможно, просто аванс на будущее. Позднее потребовалось много усилий для введения подходящих обозначений для чисел. Они стали более тяжеловесными и сильно потеряли в значимости. Теперь уже не так легко стало зачёркивать числа. С выплеснутой водой можно было потерять и ребёнка. По-видимому, древние обменивались информацией надзнаково. Это существенно выше, чем надвербально. Процесс обучения происходил в результате личного обмена идеями при непосредственном общении. Здесь было некоторое совместное погружение в информационное поле, и учитель выступал в качестве сопровождающего лица.

Мы сейчас лишены этой возможности, но нам даны другие возможности, которых не было у древних. Создана громадная система знаков, которая по своему величию и возможностям не уступает египетским пирамидам. Более того, эта система знаков обладает колоссальной избыточностью. Она задействована не более, чем на десять процентов. Остальные девяносто не просто не используются, но современное человечество даже не представляет зачем они нужны, для решения каких задач они могут быть использованы. И главное – кем использованы? Это мы на протяжении нескольких тысячелетий не можем забыть многоугольные числа или это они, каждый раз неожиданно выплывая из тумана веков, не позволяют нам себя забыть? Кто кем управляет, люди знаками или знаки людьми? Математическое осмысление этой системы и этих вопросов – вот, в сущности, основная проблема теоретической информатики.

Заключение

Здесь необходимо сказать хотя бы несколько слов о том, что не вошло в эту книгу. Прежде всего это теория разбиения чисел и метод производящих функций Эйлера. Кроме того, полновесный курс должен включать теорию упаковок. Однако, даже при очень беглом изложении всё перечисленное составляет полновесный односеместровый курс лекций. Авторы планируют подготовить соответствующее учебное пособие для студентов высших технических учебных заведений.

Библиографический список

1. Шеннон К. Работы по теории информации и кибернетике / К. Шеннон. М., 1963, 529 С.

2. Гельфонд А.О., Исчисление конечных разностей / А.О. Гельфонд, ОНТИ, 1936, ч.1, 1963 – полный вариант монографии, 1-е издание 1952 год; 4-е издание 2006 г.

3. Винер Н. Преобразование Фурье в комплексной области / Н. Винер, Р. Пэли. М., Наука, 1964 г.

4. Рвачев В.Л. Неклассические методы теории приближений в краевых задачах / В.л. Рвачев, В.А. Рвачев. Киев, Наукова Думка, 1979 г.

5. Полиа Г. Задачи и теоремы из анализа /Г. Полиа, Г. Сегё. М.: Наука, 1978, т.1. С. 144, 208, задача 23.

6. Марков А.А. Исчисление конечныхъ разностей / А.А. Марков. Одесса: Матезисъ, 1910, 274 С.

7. Эдвардс Г. Последняя теорема Ферма. Генетическое введение в алгебраическую теорию чисел / Г. Эдвардс. М., Мир., 1980, 484 С.

8. M. Marden, The geometry of the zeros of a polynomial in a complex variables, № 3, AMS. Providence, 1966, Chapter II. The critical points of a polynomial and some of their generalizations, p. 14-31.

9. Грэхем Р. Конкретная математика. Основание информатики / Р. Грэхем, Д. Кнут, О. Паташник. М., Мир., 2006, 703 С.

10. Кнут Д. Искусство программирования для ЭВМ / Д Кнут. М., Мир., т. 1, 1976.

11. Турецкий А. Х. Теория интерполирования в задачах / А.Х Турецкий. Мн.: Выш. шк., 1968, 318 С.

12. Харди Г. Двенадцать лекций о Рамануджане / Г. Харди. М.: ИКИ 2002, 335 С.

13. Эйлер Л. Введение в анализ бесконечных / Л. Эйлер., М.: ГИФМЛ. 1961, т.1, 314 С.

14. Венков Б.А. Элементарная теория чисел / Б.А. Венков. М.-Л.: ОНТИ-НКТП, 1937, 219 С.

15. Дэвенпорт Г. Высшая арифметика / Г. Дэвенпорт. М.: Наука, 1965, 175 С.

16. Ожигова Е. П. Развитие теории чисел в России / Е. П. Ожигова. М.: УРСС. 2003, 340.С.

17. Ожигова Е.П. Что такое теория чисел / Е.П. Ожигова., М.: УРСС. 2009, 94 С.

18. Неопубликованные материалы Л. Эйлера по теории чисел. СПб: Наука, 1997, 254 С.

19. Бобров С. П. Архимедово лето / С.П. Бобров. М.: ГИДЛ. 1959, Кн. 1. 391 С.

20. Ван дер Варден Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции / Б.Л. Ван дер Варден, М.: КомКнига, 2006-2007, 459 С.

21. Агранович Ю. Я. Краткий конспект лекций по дисциплине «Вычислительная математика» / Ю.Я. Агранович, Е.В. Ефанова, М.Л. Лапшина. Воронеж: ВГТУ, 2005, 106 С.

Оглавление

Введение.................................................................................... 5

Глава 1. Теорема Шеннона о существовании пропускной способности канала без шума 7

Глава 2. Интерполяция степенными и тригонометрическими многочленами. Теорема В.А. Котельникова об отсчётах. Ортогональные функции на вещественной прямой 18

Глава 3. Пропускная способность канала с белым гауссовским шумом 30

Глава 4. Числа Фибоначчи. Пропускная способность алгоритма 39

Глава 5. Задача А.А. Маркова................................................ 45

Глава 6. Многоугольные числа.............................................. 72

Глава 7. Таблица многоугольных чисел. Уравнение Ферма (Пелля). Непрерывные дроби 84

Заключение.............................................................................. 96

Библиографический список.................................................... 97

Учебное издание

Агранович Юрий Яковлевич
Подвальный Семен Леонидович
Концевая Наталья Валерьевна
Новиков Игорь Яковлевич
Хацкевич Владимир Львович

МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРЕТИЧЕСКОЙ ИНФОРМАТИКИ

АНО «Институт ИТОУР»
394036, г. Воронеж, пр-т Революции, 26/28.

Отпечатано в типографии ИП Алейникова О.Ю.
394024, г. Воронеж, ул. Ленина, 86Б, 2.

Бумага офсетная. Печать трафаретная.
Формат 60´84/16. Усл. печ. л. 6,25. Тираж 200 экз.

Дата добавления: 2018-09-22; просмотров: 239; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!