Транспортная задача с ограничениями на пропускную способность

⇐ ПредыдущаяСтр 6 из 7Следующая ⇒

Транспортная задача с ограниченными пропускными спосо6ностями коммуникаций решается с дополнительным ограничением: , где d_ij - пропускная способность звена (i, j) в единицу времени. Математическая модель задачи такова:

при ограничениях

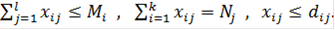
Эта задача разрешима при выполнении условий

Для транспортной задачи с ограниченными пропускными способностями справедливы следующие условия оптимальности полученного решения:

[8]

Транспортная задача по критерию времени

Кроме транспортной задачи по критерию стоимости существует задача транспортного типа по критерию времени. Постановка такой задачи состоит в следующем.

Дана матрица времени (t_ij) _kl, где t_ij - время на перевозку груза из i-того пункта отправления в j-тый пункт назначения. Матрица перевозок грузов (x_ij) _kl, где x_ij - количество перевозимого груза из i-того пункта отправления в j-тый пункт назначения. Известно также наличие груза M_i и спрос на него N_j, . Требуется определить такой план перевозок, при котором весь груз будет доставлен потребителям в кратчайший срок.

Постановка транспортной задачи по критерию времени отличается от транспортной задачи по критерию стоимости лишь целевой функцией.

Если в задаче по критерию стоимости определялись минимальные транспортные издержки, то при решении задачи по критерию времени следует определить наименьший промежуток времени, за который груз будет доставлен потребителю. Решение такой задачи очень важно в случае доставки скоропортящегося продукта.

Исходный опорный план можно получить по правилам "северо-западного угла", "минимального элемента", приближенным методом. Далее просматриваем все занятые клетки и в них выбираем максимальное время t, за которое осуществляется опорный план перевозок, т.е. Т=max (t_ij), где клетки (i; k) занятые. Каждому плану перевозок будет соответствовать вполне определенное значение Т, зависящее от плана, т.е. T=f (x). Следовательно, нужно найти такой план доставки груза потребителям, для которого Т будет минимальным.

Определив максимальное значение Т для исходного плана, просматриваем ту клетку, для которой t=Т=max (t_ij). Например, такой клеткой является (p, q). Для этой клетки строится цикл, который включает в себя занятые и свободные клетки. Таких циклов может быть несколько. Однако при построении его следует учесть условия. Занятая клетка (p, q), для которой t_iq = Т будет нечетной, следующая клетка по часовой или против часовой стрелки - четная, следующая - нечетная и т.д. Цикл состоит из двух полуциклов - четного и нечетного. Для нечетных клеток цикла обязательно должна быть загрузка больше нуля, а для четных - время меньше Т. Свободные клетки, для которых время t_ij> Т, прочеркиваются и в расчет не принимаются.

Построив цикл для разгрузочной клетки (p, q), для которой t (p, q) = Т, определяем наименьшую загрузку в нечетных клетках цикла. Полученное количество груза вычитается из грузов нечетных клеток и добавляется к числам четных клеток цикла. При этом может оказаться, что после смещения по циклу клетка (p, q) не разгрузится, тогда снова строится цикл и производится разгрузка клетки до тех пор, пока количество груза не станет равным нулю. После разгрузки клетки, имеющей максимальный промежуток времени, получаем новый план перевозок, для которого отыскивается разгрузочная клетка и снова производится процедура построения цикла и смещения груза по циклу. Процесс продолжается до тех пор, покуда можно будет строить разгрузочные циклы. В случае невозможности построить такой цикл в полученных занятых клетках плана выбираем максимальное время, которое и будет искомым по реализации оптимального плана. [9]

Дата добавления: 2018-09-22; просмотров: 518; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 Следующая ⇒

Мы поможем в написании ваших работ!