Необходимые и достаточные условия
В следующих предложениях вместо многоточия поставьте слова «необходимо, но недостаточно» или «достаточно, но не необходимо», а где возможно «необходимо и достаточно» так, чтобы получилось истинное утверждение:
Задача 1. Пусть на отрезке [a, b] определена непрерывная функция f(x) имеющая на промежутке [a, b] конечные производные, тогда:
Для того, чтобы функция f(x) была постоянной на отрезке [a, b] необходимо и достаточно, чтобы 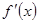 =0 для
=0 для 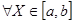 .
.
Решение:
F(x)=const на [a, b] 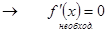 - истина
- истина
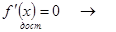 F(x)=const на [a, b] – истина
F(x)=const на [a, b] – истина
Задача 2. Для того, чтобы два вектора 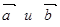 в пространстве были перпендикулярными, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю
в пространстве были перпендикулярными, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю
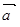 ┴
┴ 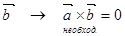 - истина
- истина
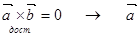 ┴
┴ 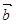 - истина
- истина
Задача 3. Для того, чтобы уравнение 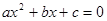 имело действительные корни, необходимо и достаточно, чтобы
имело действительные корни, необходимо и достаточно, чтобы 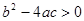 .
.
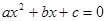 имело действительные корни
имело действительные корни 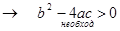

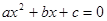 имело действительные корни
имело действительные корни
Задача 4. Для того, чтобы в точке x0 функция f(x) имела экстремум, необходимо, чтобы 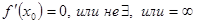
Решение:
функция f(x) в точке x0 имеет экстремум 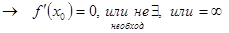 - истина
- истина
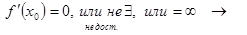 функция f(x) в точке x0 имеет экстремум – ложь
функция f(x) в точке x0 имеет экстремум – ложь
контрпример: 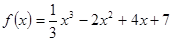 .
.
Задача 5.Для того, чтобы четырехугольник был квадратом, необходимо, но не достаточно, чтобы его диагонали были перпендикулярны.
Решение:
ABCD – квадрат 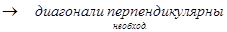 - истина
- истина
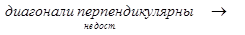 ABCD – квадрат – ложь
ABCD – квадрат – ложь
 B
B
контрпример: A C
D
Задача 6.Для того, чтобы уравнение cos x = a имело решение, необходимо, но не достаточно, чтобы 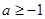 .
.
Решение:
Cos x = a - имеет решение 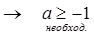
|
|
|
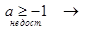 Cos x = a - имеет решение – ложь
Cos x = a - имеет решение – ложь
контрпример: a = 3.
Задача 7. Для того, чтобы в точке x0 функция f(x) имела разрыв второго рода, достаточно, чтобы 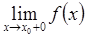 = ∞.
= ∞.
Решение:
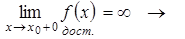 функция f(x) в точке x0 имеет разрыв второго рода – истина.
функция f(x) в точке x0 имеет разрыв второго рода – истина.
Задача 8. Для того, чтобы выражение x2 – 2x – 3 равнялось нулю, достаточно, но не необходимо, чтобы x = -1.
Решение:
x2 – 2x – 3 = 0 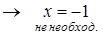 - ложь
- ложь
контрпример: x = 3.
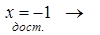 x2 – 2x – 3 = 0 – истина
x2 – 2x – 3 = 0 – истина
Анализ и синтез релейно-контактных схем
Одно из применений алгебры высказываний – анализ и синтез релейно-контактных схем.
Еще в 1910 году физик П.С. Эренфест указал на возможность применения аппарата алгебры логики при исследовании релейно-контактных схем. Каждой схеме можно поставить в соответствие некоторую формулу алгебры высказываний, и каждая формула алгебры высказываний реализуется с помощью некоторой схемы.
Рассмотрим 2-х-полюсные переключатели, т.е. такие, которые имеют два состояния: «замкнуто» - 1, «разомкнуто» - 0. На схеме будем изображать: 
Определение 7. Переключатель, который сблокирован с X так, что он замкнут, если X разомкнут, и разомкнут, если X замкнут, называется инверсным и обозначается 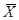 .
.
Конъюнкция двух высказываний X и Y будет представлена двухполюсной схемой с последовательным соединением двух переключателей X и Y.
|
|
|
Эта схема пропускает ток тогда и только тогда, когда истины и X, и Y одновременно, то есть истина конъюнкция X&Y.

X&Y
Дизъюнкция двух высказываний X и Y изобразится двухполюсной схемой с параллельным соединением двух переключателей X и Y.
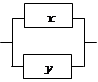
X 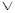 Y
Y
Эта схема пропускает ток в случае, если истинно высказывание X или истинно высказывание Y, то есть истина дизъюнкция X  Y.
Y.
Таким образом, всякую булеву формулу можно трактовать как некоторую последовательно-параллельную схему от 2-х-полюсных переключателей. Все свойства булевых операций переносятся на соответствующие операции над переключателями. Формула, которую можно составить для каждой схемы называется функцией проводимости схемы, а таблица значений – условиями работы схемы.
Определение 8. Две схемы называются равносильными, если имеют одинаковые функции проводимости.
Анализ схемы заключается в следующем: для данной схемы составляется функция проводимости, которая на основании законов булевых функций упрощается и для нее строится новая, более простая схема, которая обладает теми же электрическими свойствами.
|
|
|
Синтез схем заключается в построении схем с заданными электрическими свойствами. На основании заданных электрических свойств строится таблица условий работы схемы и затем функция проводимости, представляющая собой СДНФ, а по ней строится схема.
Задача 1. Составить РКС, обладающая следующей функцией проводимости:
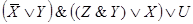
Решение:
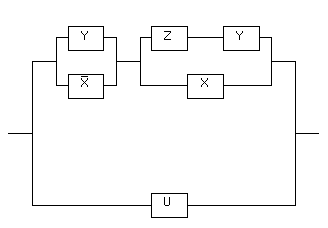
Задача 2. Составить РКС обладающая следующей функцией проводимости:
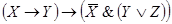
Решение:
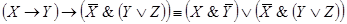
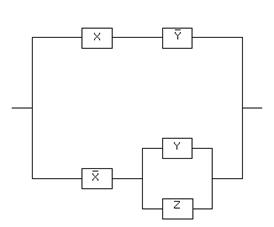
Задача 3. Составить РКС обладающая следующей функцией проводимости:
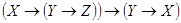
Решение:
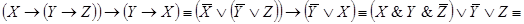

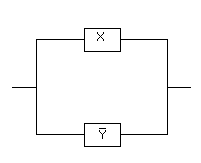
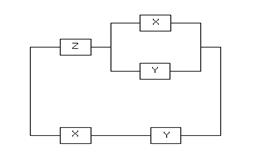
Задача 4. Упростить РКС:
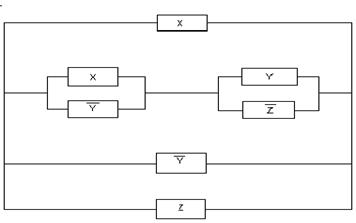
Решение:
Ей соответствует функция проводимости:
F(X,Y,Z) 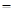
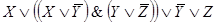
F(X,Y,Z) 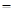
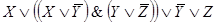
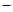
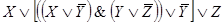
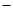
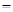
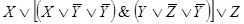
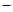
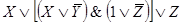

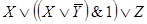

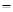

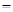
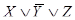
Этой же функции проводимости соответствует более простая схема.
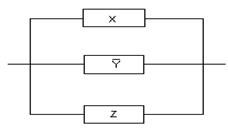
Задача 5. Упростить РКС:
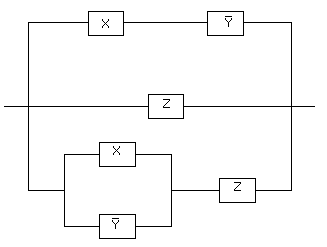
Решение:
Ей соответствует функция проводимости:
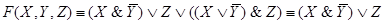
Этой же функции проводимости соответствует более простая схема.
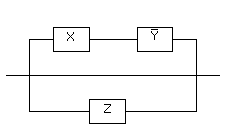
Задача 6. Упростить РКС:
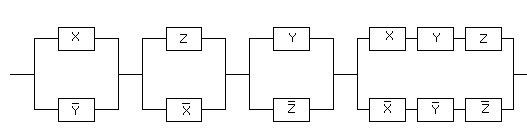
Решение:
Ей соответствует функция проводимости:
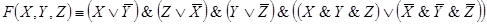
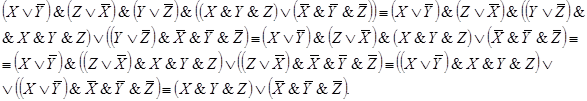
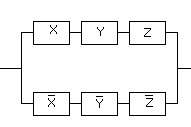
Задача 7. Какой контакт необходимо вставить в вакантное место, чтобы функция проводимости полученной схемы стала бы равна данной булевой функции:
|
|
|
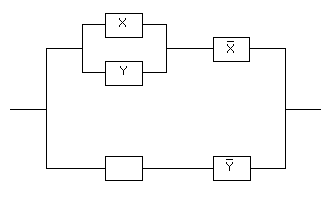
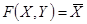
Данной схеме соответствует функция проводимости:
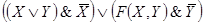
Решение:
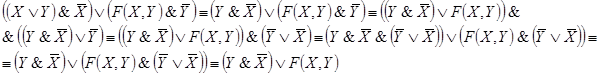
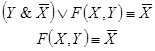
Задача 8. Какой контакт необходимо вставить в вакантное место, чтобы функция проводимости полученной схемы стала бы равна данной булевой функции:
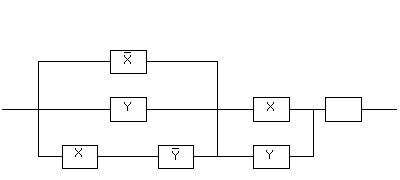
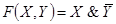
Данной схеме соответствует функция проводимости:
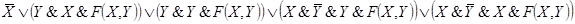
Решение:
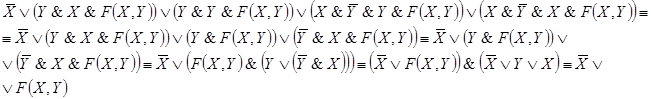
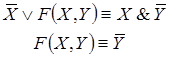
Задача 9. Какой контакт необходимо вставить в вакантное место, чтобы функция проводимости полученной схемы стала бы равна данной булевой функции:
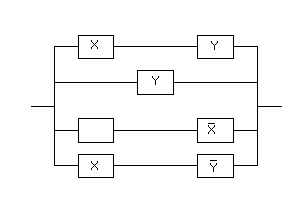
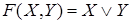
Данной схеме соответствует функция проводимости:
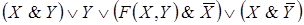
Решение:

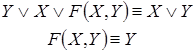
Задача 10. Построить РКС с четырьмя переключателями, которая проводит ток тогда и только тогда, когда замыкаются не все переключатели, а только некоторые из них.
Решение:
Составим таблицу значений функции проводимости F (X, Y, Z, T) этой схемы:
| X | Y | Z | T | F (X, Y, Z, T) | |
| 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 | 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 | 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 | 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 | 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 | * * |
В правом столбце звездочками отметим те строки, на которых функция F (X, Y, Z, T) обращается в 0, запишем для неё выражение, используя СКНФ, потому что наборов значений аргументов, на которых функция обращается в 0, значительно меньше, чем наборов значений аргументов, на которых функция обращается в 1, и значит, СКНФ будет более простой, чем СДНФ:
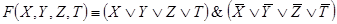
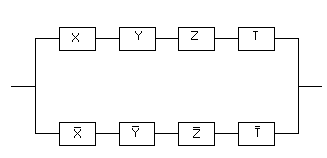
Задача 11. Построить схему с тремя переключателями, которая замыкается тогда и только тогда, когда замкнут либо один, либо два переключателя. При построении использовать не более шести контактов.
Решение:
Составим таблицу значений функции проводимости F (X, Y, Z) этой схемы:
| X | Y | Z | F (X, Y, Z) | |
| 1 1 1 0 1 0 0 0 | 1 1 0 1 0 1 0 0 | 1 0 1 1 0 0 1 0 | 0 1 1 1 1 1 1 0 | * * * * * * |
В правом столбце звездочками отметим те строки, на которых функция
F (X, Y, Z, T) обращается в 1, запишем для неё выражение, используя СКНФ, потому что наборов значений аргументов, на которых функция обращается в 0, значительно меньше, чем наборов значений аргументов, на которых функция обращается в 1, и значит, СКНФ будет более простой, чем СДНФ:
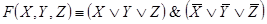
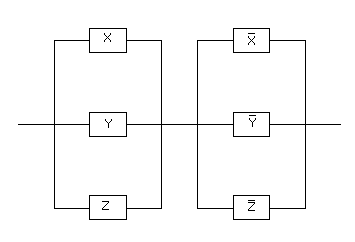
Задача 12. Требуется составить схему с четырьмя переключателями X, Y, Z, T. Схема должна проводить ток тогда и только тогда, когда будут замкнуты переключатели X и Y или Z и T.
Решение:
Составим таблицу значений функции проводимости F (X, Y, Z, T) этой схемы:
| X | Y | Z | T | F (X, Y, Z, T) | |
| 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 | 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 | 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 | 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 | 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 | * * |
В правом столбце звездочками отметим те строки, на которых функция
F (X, Y, Z, T) обращается в 1, запишем для неё выражение, используя СДНФ:
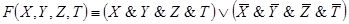
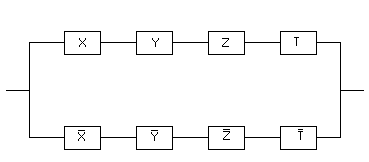
Задача 13. Построить контактную схему для оценки результатов некоторого спортивного соревнования тремя судьями при следующих условиях: судья, засчитывающий результат, нажимает имеющуюся в его распоряжении кнопку, а судья, не засчитывающий результат, кнопки не нажимает. В случае, если кнопки нажали не менее двух судей должна загореться лампочка (положительное решение судей принято простым большинством голосов).
Работа РКС описывается функцией Буля трех переменных F (X, Y, Z), где переменные высказывания X, Y, Z означают:
X – судья X голосует «за»
Y – судья Y голосует «за»
Z – судья Z голосует «за»
Таблица истинности функции F (X, Y, Z) имеет вид:
| X Y Z | F(X, Y, Z) |
| 1 1 1 | 1 |
| 1 1 0 | 1 |
| 1 0 1 | 1 |
| 0 1 1 | 1 |
| 1 0 0 | 0 |
| 0 1 0 | 0 |
| 0 0 1 | 0 |
| 0 0 0 | 0 |

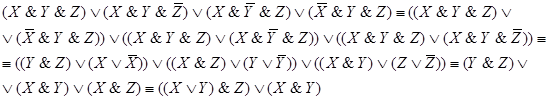
Этой же функции проводимости соответствует более простая схема.
Дата добавления: 2018-09-22; просмотров: 304; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
