Межвременной потребительский выбор И. Фишера
Ирвинг Фишер выдвинул гипотезу о том, что при принятии потребительских решений рациональные экономические субъекты учитывают не только текущий, но и будущий доход, получаемый на протяжении жизни, и поставил проблему межвременного потребительского выбора.
Уравнение межвременного бюджетного ограничения потребителя показывает все возможные сочетания потребления в 1‑м и во 2‑м периодах. Факторами, определяющими функции потребления и сбережения, являются доход и процентная ставка.
Функция потребления И. Фишера отражает зависимость потребительских расходов от текущей (денежной) стоимости дохода за все периоды жизнедеятельности.
Проблема выбора стоит перед потребителем, живущим в двух временных периодах: молодость (доход Yl) и старость (доход Y2).
В первый период индивид потребляет и сберегает:
Yl = C1 + S1(3.1)
Тогда:
C1 = Yl– S1; S1 = Yl– C1, (3.2)
где C1 – потребление 1‑го периода; S1 – сбережения 1‑го периода.
Если разница между Yl и C1 – отрицательная величина, то экономический субъект вынужден заимствовать. В дальнейшем он выплачивает долг и проценты по нему.
Во втором периоде индвивид имеет доход Y2. Он потребляет, но не сберегает, однако пользуется сбережениями (включая процент по ним), сделанными заблаговременно в первый период жизни. Тогда:
С2 = Y2+ S2(1 + r) = Y2+ (Y1 – C1)(1 + r)), (3.3)
где r – реальная ставка процента.
Раскроем скобки в выражении (3.3) и перенесем влево элементы потребления. В результате получим:

Разделим обе части уравнения (3.4) на 1+r, тогда:

Мы получили уравнение межвременного бюджетного ограничения потребителя, которое показывает, какой суммой средств должны располагать потребители в течение двух жизненных периодов.
Предпочтения потребителя между потреблением в 1‑м и 2‑м периодах представлены с помощью кривых безразличия.
Каждая кривая безразличия характеризует равный уровень полезности для потребителя разных наборов потребления сегодня и в будущем. Для потребителя предпочтительны более высокие кривые безразличия, так как они обеспечивают большее потребление.
Потребители, максимизируя свою полезность, стремятся достичь более высокой кривой безразличия. Однако их стремления ограничены межвременным бюджетным ограничением.
Оптимальное сочетание потребления 1‑го и 2‑го периодов достигается в точке О, где наивысшая кривая безразличия, которую может достичь потребитель, является касательной к линии бюджетного ограничения (рис. 3.4).
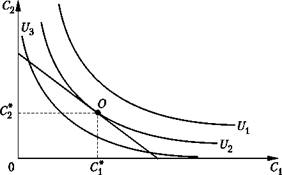
Рис. 3.4. Оптимум потребителя
Наклон кривой безразличия выражает предельную норму замещения (MRS).
Наклон линии бюджетного ограничения равен 1 + r. Следовательно, в точке О: MRS = 1 + r.
На потребление оказывают влияние:
• рост дохода;
• изменение уровня процентной ставки.
Рост дохода в 1‑м или 2‑м периодах сдвигает линию бюджетного ограничения вправо. Если потребление в 1‑м и 2‑м периодах– нормальные блага, то рост дохода увеличивает потребление в обоих периодах.
Изменение реальной процентной ставки. С ростом процентной ставки потребление в первом периоде сократится, а во втором увеличится.
Влияние роста реальной ставки процента выражается в эффекте дохода и эффекте замещения.
Эффект дохода – изменение в потреблении, вызванное переходом к более высокой кривой безразличия.
Эффект замещения – изменение в потреблении, вызванное изменением относительной цены потребления в оба периода. Если ставка процента повышается, то потребление 2‑го периода становится более дешевым по сравнению с потреблением в 1‑м периоде.
Из изложенного вытекает, что потребление зависит от текущей стоимости дохода в данном периоде и дисконтированной стоимости будущего дохода:

Если существуют ограничения по заимствованию, т. е. С1 ≤ Y1, размер потребления зависит только от уровня текущего дохода, т. е. С1 =Y1.
Ограничение по заимствованию (ограничение ликвидности) – это предельная величина кредита частным лицам, предоставляемая финансовыми учреждениями, чтобы уменьшить заблаговременное расходование будущих доходов.
Дата добавления: 2018-09-22; просмотров: 396; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
