Дана система линейных уравнений
Nbsp; МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра высшей математики Контрольная работа №1 по курсу "Высшая математика - 1" Вариант 1.6 Преподаватель Студент группы __________ / доц. Тупой И.И. / __________ / Пупкин В.И./ ___________2002 г. до н.э. 35 ноября 2002 г. до н.э. Томск 2002 до н.э. 1. Найти матрицу D = ( CA – BA ), если , , Решение: 1) 2) 3) Ответ: 2. Вычислить определитель Решение: Используя свойства определителя: 1) умножим первую строку на 2 и отнимем от второй строки 2) умножим первую строку на 4 и отнимем от четвертой 3) первую строку отнимем от третьей Получим *Сумма D найдена по правилу «треугольников» Ответ: D=57
Решить матричное уравнение
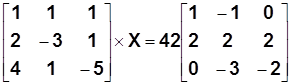
Решение:
Обозначим 
и 
Вычисляем
,
значит матрица А невырожденная, а потому имеет обратную. Элементы
обратной матрицы находим по формуле 
Алгебраические дополнения всех элементов матрицы А, т.е. элементы присоединенной матрицы
|
|
|
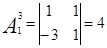
Обратная матрица 
Находим X из уравнения AX=B, где A-1AX=BA-1, но A∙A-1=E (E-единичная матрица).
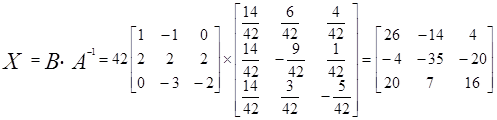
Ответ:
4. При каком значении параметра q , если оно существует, обведенный минор матрицы А является базисным? Матрица А имеет вид:
Решение:
1) Определяем значение минора 
, значит ранг матрицы не меньше двух.
2) Через λ1 и λ2 обозначим коэффициенты линейной комбинации, с помощью которых четвертая строка выражается через первые две
, получим систему
Решаем подсистему
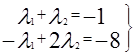
q=9
Второе и пятое уравнения превращаются в тождества.
3)Преобразуем матрицу А:
Так как в полученной матрице вторая и третья строки пропорциональны, то значит базисный минор равен 2–м, и q=9.
5. Относительно канонического базиса в R 3 дано четыре вектора f 1 (4, 2, -1), f 2 (5, 3, -2), f 3 (3, 2, -1), x (12, 7, -3). Доказать, что векторы f 1, f 2, f 3 можно принять за новый базис в R 3 . Найти координаты вектора x в базисе fi .
Решение:
Составим матрицу В, записав в ее столбцы координаты векторов f1, f2, f3, т.е.
Находим определитель матрицы В: det B=1≠0, значит векторы f1, f2, f3 линейно независимы, а потому могут быть приняты в качестве базиса R3.
|
|
|
Матрица В невырождена, и поэтому имеет обратную (В-1).
Находим 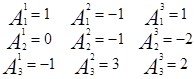В-1:
В-1= 
Новые координаты вектора x обозначим η1, η2, η3 и найдем их по формуле:
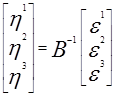
Ответ:
Новые координаты вектора x=(2, -1, 3)
Доказать, что система
имеет единственное решение. Неизвестное x 2 найти по формулам Крамера. Решить систему методом Гаусса.
Решение:
а) Вычислим определитель системы
,
значит система имеет единственное решение.
б) Находим определитель D2 (в определителе D второй столбец заменен столбцом свободных членов)
.
По формуле Крамера 
в) Решаем данную систему методом Гаусса.
Записываем расширенную матрицу системы и преобразуем ее к треугольному виду, действуя только со строками
Данная система эквивалентна системе
,
из которой находим: x4=-1, x3=1, x2=-2, x1=2.
Решение системы (2, -2, 1, -1).
Дана система линейных уравнений
Доказать, что система совместна. Найти ее общее решение. Найти частное решение, если x 2 =-1
|
|
|
Решение:
Применим к системе метод Гаусса. Запишем расширенную матрицу системы и преобразуем ее, действуя только со строками, чтобы увидеть базисный минор.
Третью строку можно вычеркнуть, не меняя ранга матрицы.
В результате получим матрицу
.
В качестве базисного выберем минор 
, т.е. неизвестные x1 и x2 приняты в качестве зависимых, а x3 и x4 – в качестве свободных.
- общее решение системы.
Найдем частное решение системы. Так как x2= -1, то, подставляя во второе уравнение это значение, получим x3= -x4. Если x3= -1, то x4= 1, а x1= 3. Получили частное решение (3, -1, -1, 1)
8 Найти | a |, если
, 
, 
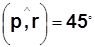
Решение:
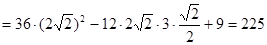
Ответ:
|a|=15
9. Найти угол (в градусах), образованный вектором [ AB , BD ] с осью OY , если A (-5, 1, 1); B (1, -2, -2); D (-1, -4, -1).
Решение:
Запишем координаты векторов AB = {6, -3, -2} и BD = {-2, -2, 1}.
Вектор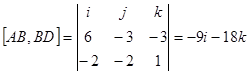 
Находим угол между вектором [AB, BD] и осью OY по формуле
; 
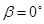
10. Линейный оператор A действует в R 3 → R 3 по закону Ax =(3 x 1 , - x 1 + x 3 , 2 x 1 -4 x 2 +4 x 3 ), где x ( x 1 , x 2 , x 3 ) – произвольный вектор. Найти матрицу A этого оператора в каноническом базисе. Доказать, что вектор x (1, 3, 10) является собственным для матрицы A . Найти собственное число λ0, соответствующее вектору x . Найти другие собственные числа, отличные от λ0. Найти все собственные векторы матрицы A и сделать проверку.
|
|
|
Решение:
а) Так как A(1, 0, 0)=(3, 0, 0), A(0, 1, 0)=(-1, 0, 1), A(0, 0, 1)=(2, -4, 4), то записав в столбцы координаты полученных векторов найдем матрицу A
б) Проверим, что вектор x=(1, 3, 10) является собственным матрицы A.
Так как Ax=3x, то вектор x(1, 3, 10) собственный и отвечает собственному λ0=3.
в) Чтобы найти другие собственные числа, составляем характеристическое уравнение
Вычисляем определитель (3-λ)(-λ)(4-λ)+4(3-λ)=0
(3-λ)(-4λ+λ2+4)=0
λ1=2; λ2=3
г) Так как λ0=λ3=3, то можно найти собственный вектор для λ1=2 и составить характеристическое уравнение
x1=0, а x3=2x2, если x2=1, то нашли собственный вектор (0, 1, 2).
д) Проверка
Дата добавления: 2018-09-22; просмотров: 431; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!