Механический смысл производной второго порядка

Матрица – это таблица чисел расположенных mстрок и в n столбцов. Обозначение Am*n , круглыми или квадратными скобками. Квадратная матрица – матрица в которой кол-во строк равно кол-ву столбцов. m=n, где nявл. порядком квадратной матрицы. 2. Определитель это числе , вычисляемое по установленным правилам. Обозначение[Amn]или detA. В отличии от матрицы, которая представляет собой таблицу чисел, определитель это число, которое определенным образом ставиться в состав матрицы. 3. Определитель первого порядка = самому числу, т.е. [a11]=a11 Определитель второго порядка = произведение элементов главной диагонали минус произведение элементов побочной диагонали. 4. Минором Mijэлемента aijназывается определитель , получаемый из данного определителя, путем мысленного вычеркивания строки и столбца на пересечении которых находиться выбранный элемент Алгебраическим дополнением Aijэлемента aijназывается минор Mij взятый со знаком «+» если сумма индексов четная, или со знаком «-» если сумма индексов нечетная, Aij= (-1)i+j*Mij 5. Определитель третьего порядка вычисляют путем расписывания по элементам первой строки разложением по элементам i-й строки; i=1,2,3,…,n разложением по элементам j-й столбца; j=1,2,3,…,n 6. 1.Если какой-либо столбец(строка) = 0, то его определитель = 0 2.Если все элементы какой-либо строки(столбца) умножить на число h то его определитель увеличиться в hраз 3.При транспонировании матрицы его определитель не меняется 4.При перестановке двух строк (столбцов) местами, знак определителя меняется на противоположный 5.Если квадратная матрица содержит две одинаковые строки(столбца) то её определитель = 0 7. 6.Если элементы двух строк(столбцов) матрицы пропорциональны, то её определитель = 0 7.Сумма произведений элементов какой-либо строки(столбца) матрицы на алгебраическое дополнение элементов другой строки(столбца) этой матрицы = 0 8.Определитель матрицы не изменяется, если к элементам какой-либо строки(столбца) матрицы прибавить элементы другой строки(столбца), предварительно умноженные на одно и тоже число. 9.Сумма произведений произвольных чисел на алгбро.дополнение элементов любой строки(столбцов) = определителю матрицы полученной из данной путем замены элементов этой строки на числа b1,b2,b3,…,bn 10. Определитель произведения двух квадратных матриц = произведению их определителей. [C]=[A]*[B], гдеC=A*B, AиBматрицыn-го порядка 8. Определитель квадратной матрицы = сумме произведений элементов любой строки(столбца) на их алгебр.дополнения. 9. Виды матриц: матрица-строка, матрица-столбец, квадратная матрица, диагональная матрица, нулевая матрица, единичная матрица. Пара чисел m и n размерностью матрицы. Порядок матрицы- это другое название размерности матрицы. Главная диагональ это линия на которой расположены элементы где m=n, a11, a22,a33, и так далее. Квадратная матрица – матрица где кол-во строк = кол-ву стоблцов Треугольная матрица – это квадратная матрица у которой все элементы над или под главной диагональю = 0 Вырожденная матрица – это кв.матрица определитель которой = 0 Невырожденная матрица – это кв.матрица определитель которой отличен от нуля. Транспонированная матрица – если в исходной матрице элементы каждой строки расположить в виде столбцов с теми же номерами, то получиться транспонированная матрица. Матрица состоящая из одной строки, называется матрицей(вектором)- строки, а из столбца- матрицей(вектором)-столбцом 10. Матрицы называются равными , если у них одинаковое число строк и столбцов, и все соответствующие элементы совпадают Матрицы одинаково измерения – m*n– размерность 11. Нулевая матрица – это матрица элементы которой = 0 Диагональная матрица – элементы матрицы которой номер столбца = номеру строки(i=j) Скалярная матрица – это диагональная матрица , элементы главной диагонали которой равны. Единичная матрица – квадратная матрица, элементы главной диагонали которой = 1 а остальные элементы = 0 12. Линейные операции над матрицей: умножение матрицы на число, сложение вычитание, и умножение матриц. Сумма: матрицы складываются поэлементно Разность двух матриц одинаково размера определятся через предыдущие операции: A-B=A+(-1)B Складывать матрицы можно только одинаковой размерности При умножении числа на матрицу, каждый элемент матрицы умножается на это число. Да всегда. Свойства линейной операции на матрицами: A+B=B+A(коммутативность сложения матриц) (A+B)+C= A+(B+C) (ассоциативность сложения матриц) A+0=A A+(-A)=0 α*(β*A)=(α*β)*A(ассоциативность относительно умножения чисел) (α+β)*A=α*A+β*A(дистрибутивность умножения на матрицу относительно сложения чисел) α *(A+B)= α*A+ α*B(дистрибутивность умножения на число относительно сложения матриц) 1*A=A 13. Согласованные матрицы – если кол-во столбцов в первой строке = кол-ву строк во 2 матрице , то матрицы согласованные. Умножение матриц возможно, только если они согласованные. Умножение матрицы A на матрицу B определено, когда число столбцов первой матрицы = силу строк второй матрицы. Тогда произведение матриц Am*k*Bk*nназывается такая матрица Cijравная сумме произведению элементов i-й строк матрицы A на соответствующие элементы j-го столбца матрицы B 14. Нет 15. ————— 16. ————— 17. Линейное алгебраическое уравнение с n неизвестными в линейной алгебре это система уравнений вида a11*x1+a12*x2+…+a1n*xn=b1 a21*x1+a22*x2+…+a2n*xn=b2 a31*x1+ a32*x2+…+ a3n*xn=b3 Система m линейных алгебра.уравнений с n неизвестными называется однородной , если все свободные члены bi=0, где i=1,2,3…m Неоднородный- наоборот, иначе. Система уравнений называется совместной если она имеет хотя бы одно решение, несовместной , если она не имеет решений. Совместная система уравнений называется определенной если она имеет единственное решение, неопределенной если она имеет более одного решения Решение системы линейных – это набор значений переменных при подстановке которых в систему уравнений каждая из уравнений превращается в числовое тождество Чтобы проверить правильность решения, надо подставить его в каждое матричное уравнение, и убедиться что оно обращается в тождество. 18. Правило Крамера: Если в системе n линейных уравнений с n неизвестными ∆≠0, то система имеет решение и при этом только единственное Формула: xj=∆j/∆ (j=1,2,3,…n) 19. Метод Гауса 1. Записать расширенную матрицу 2. С помощью законов алгебраических преобразований, а именно с помощью эквивалентного преобразования, получаем нули под главной диагональю расширенной матрицы.(Прямой метод Гауса) При получении нулей под главной диагональю в первом столбце используют первую строчку и первый элемент в ней, при получении нулей под главной диагональю во 2-ом столбце, используют вторую строчку(уже новую) и второй элемент в ней. 3. После получения 0-ей под гл.диагональю заполняют систему уравнений , но уже с новыми коэффициентами 4. Выполнение обратного хода в методе Гауса Обратный ход в методе Гауса заключается в последовательном нахождении неизвестных путем подстановки найденных величин в предыдущие уравнения Три случая: 1. Если ∆≠0, то система имеет единственное решение 2. ∆=0 и нет противоречий, то система имеет множество решений 3. ∆=0 и есть противоречия, то система не имеет решений Расширенная матрица – матрица A в которой дополнительно включен столбец свободных членов Главная матрица – матрица, составленная из коэффициентов перед неизвестными. 20. 21. Система линейных уравнений совместна и только тогда, когда ранг матрицы системы = рангу расширенной матрицы этой системы. Если ранг матрицы совместной системы = числу переменных, т.е. r=n, то система имеет единственное решение. Тривиальное решение – это нулевое решение x=(0,…,0) системы Для сущ. Нетривиального решения необходимо и достаточно чтобы r=rangA<n(при m=nэто условие означает что detA=0) 22. ————— 23. ————— 24. ————— 25. Матричный способ решения С.Л.А.У. – пусть для матрицы A порядка nна n сущ. Обратная матрица A-1. Умножим обе части матричного уравнения A*X=B слева на A-1Имеем A-1(A*X)=A-1*B так как для( A-1*A)*X=A-1*B а по определению обратной матрицы A-1*A=E (Eединичнаяматрица), поэтомуA-1(A*X)=A-1*B =>E*X=A-1*B=> X=A-1*B Матричная форма записи: A*X=B ;A: матрица из коэффициентов перед неизвестной ;B: матрица-столбец свободных членов ;X: матрица-столбец с именами 26. Векторная величина – величина имеющая численное значение и направление. Скалярная величина – величина имеющая численное значение, но не имеющая направление. Вектор – направленный отрезок AB с начальной точкой Aи с конечной B Длина и направление, точку приложения вектора 27. Свободный вектор – вектор, который можно переносить в любую точку пространства без изменения направления и величины Скользящие вектора – векторы которые можно вдоль линии их действия без изменения направления и величины. Закрепленные вектора перемещать нельзя Все они используются в математике. 28. Единичный вектор – любой вектор имеющий длину равную единице(I,j,k единичные вектора направленные вдоль осей OX,OY,OZ соответственно) Нулевой вектор – вектор у которого начало и конец совпадают. Коллинеарные вектора- вектора которые паралельны друг другу или лежат на одной прямой. Сонаправленные вектора-паралельные вектора которые направлены в одну сторону. Комплонарные вектора – векторы которые лежат в одной плоскости 29. Правило треугольника : суммой 2-х векторов aи bназывается такой вектор c у которого начало вектора совпадает с началом вектора a а конец сконцом вектора b, при условии что начало вектора b совпадает с концом вектора a Правило параллелограмма : вектор c в данном случае представляет собой параллелограмма . Правило многоугольника:сумма нескольких векторов построенных последовательно = вектору начало которого совпадает с началом первого вектора а конец совпадает с концом последнего (аналогично треугольному методу) Правило параллелепипеда : вектор d=a+b+c определённы таким образом, представляет диагональ параллелепипеда , построенного на векторах a,bи cне лежащих в одной плоскости. 30. Задается единичными векторами Прямоугольная система координат – прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве Прямоугольная система координат в 3-х мерном пространстве образуется 3-я взаимно перпендикулярными осями координат OX,OY,OZОси координат пересекаются в точке О которая является началом координат на каждой оси выбрано положительно направление Прямая система координат на плоскости образуется двумя взаимно перпендикулярными осями координат x’xи y’y. Оси координат пересекаются в точке О которая явл. началом координат. Положение точки А на плоскости определяется двумя координатами xи y. Проекция вектора на плоскости находится произведением модуля вектора на cosα. Перпендикуляр на ось (в 2-х мерном пространстве.) По Базису Нужно опустить перпендикуляр от точки к каждой оси 31. Ортом вектора называется вектор единичной длинны имеющий то же направление что и общий вектор Орт вектора можно получить разделив вектор на его длину Любой вектор 3-х мерного пространства можно выразить единственным способом по правилу Базиса . Базисный вектор –множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственны образцом представлен в виде линейной комбинации векторов из этого множества. Декартовая система – оси XYZ перпендикулярны друг другу. Вдоль каждой оси имеется единичный вектор. Все 3 есть базисная декартовая система координат. 32. Что бы разложить вектор b по базисным векторам , необходимо найти коэффициенты при которых линейная комбинация векторов = вектору b, x1a’1+…xna’n=b при этом коэффициенты x1…xnназываются координатами вектора b Составленный вектор на оси - это сумма вектора aна координаты axi+ayj+azk. F=(F*cosα)*i+(F*sinα)*j Проекция вектора на ось длина вектора на cosα Разница между прекцированием Отилад-ся по осям , достраиваем до перпендикуляра строят диагональ сквозь пераллелепипеда. Описать по базису 33. Что бы найти координаты вектора нужно из координат конца вычесть координаты начала. a=b, когдаax=bxay=by az=bz Модуль вектора = квадратному корню из суммы квадратов координат. 34. Условие коллиниарности векторов: Два вектора коллиниарные если отношения их координат равны Два вектора коллиниарные если их векторное призведение =0 35. ————— 36. Линейными векторами над векторами называют операции сложения и вычитания, умножение вектора на число. a+b=b+a(переместительное св-во) (a+b)+c=a+(c+b)(сочетательное св-во) h(ma’)=(hm)a’ (h+m)a’=ha’+ma’ h(a’+b’)=ha’+hb’ 37. ————— 38. 39. 40. 41. 42. 43. 44. 45. ————— 46. 47. 48. площадь параллелограмма 49. либо 1 либо 0 50. 51. Одна вторая Площади паралелограмма 52. Смешанное произведение вектаров(a,b,c) это сколярное произведение вектораaна векторное произведение b и c 53. Модуль смешенного произведения численно равен объему параллелепипеду образованного этими векторами. 54. Перестановка любых двух сомножителей меняет знак произведения Смешанное произведение в правой декартовой системе = определителю матрицы составленной из этих вектаров Если два любых вектора коллиниарны , то произведение =0 Если все три вектора линейно зависимы то произведение =0 55. 56. = объему парралелепипеда 57. 58. Множество может быть задано перечислением всех элементов или списком. Может быть задано описанием св-в его элементов, можно задать пораждаущей процедурой. 59. Множество Аявл. подмножеством множества В если любой элемент принадлежащий А так же принадлежит В Пустое множество – это множество не имеющее ни одного элемента Два множества называются равными, если они состоят из одних и тех же элементов, т.е. каждый элемент первого множества является элементов второго множества и наоборот 60. Сумма множеств есть множество элементов, каждый из которых принадлежит тому или другому множеству 61. Произведение множеств есть множество элементов которых принадлежит и тому и другому множеству 62. Разность множеств есть множество элементов которое принадлежит одному множеству, но не принадлежит другому множеству 63. Дополнение множества это множество Aотносительно множества В 64. Множество натуральных чисел это числа используемых при счете(N) Множество целых чиселэто натуральные числа взятые со знаком + и – и еще 0(Z) Рациональное число это число представленное в виде дроби n/m где nмножество целых чисел, а m натуральных чисел(Q) Действительные числа это рациональные и иррациональные числа вместе взятые. 65. Отрезок это часть прямой , ограниченная с двух сторон точками , причем крайние точки включаются во множество Интервал- это часть прямой, ограниченная с двух сторон точками, причем обе эти точки не включаются во множество Полуинтервал- множество точек прямой, ограниченная с двух сторон, причем только одна входит в это множество. 66. Аналитическая геометрия это раздел геометрии который исследует простейшие геом. объекты 67. Зная геом. св-ва линии как найти её уравнение Зная уравнение линии, связывающие ее текущие координаты x и y найти геом. св-ва этой линии 68. Направляющий вектор прямой это вектор не равный 0 , лежащий на данной прямой или параллельной ей. 69. OM=OM0+M0M (все они вектора) 70. 71. 72. 73. Любой вектор перпендикулярный прямой 74. A:(x-x0)+B(y-y0)=0 M0(x0, y0) перпендикулярно вектору N(A,B) 75. A*x+B*y+C=0 76. ————— 77. Y=kx+bK=tgαгдеα> 0, против часовой стрелки от оси OX 78. y-y1=k(x-x1) уравнение пучка прямых 79. 80. Решением системы этих уравнений. Решением самого уравнения, приравняв его к нулю, и взяв дополнительные точки аргумента. 81. 82. Коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны(условие параллельности) A1A2 + B1B2 = 0.(условие перпендикулярности) 83. условие перпендикулярности k1 = k2 условие параллельности 84. ————— 85. Путем решения системы из этих уравнений 86. ————— 87. ————— 88. Гипербола, парабола ( х – х0 ) 2 + ( у – у 0 ) 2 = R 2 89. ( х – х0 ) 2 + ( у – у 0 ) 2 = R 2 . эллипс Гипербола парабола 90. Точка пересечений большой и мало осей и является центром эксцентриситет фокус или . Директриса эллипса 91. . Директриса гиперболы . Фокус гиперболы эксцентристет гиперболы 92. .Если перед аргументом со старшей степенью стоит «+» то его ветви направлены вверх, если же «-» то вниз 93. ————— 94. ————— 95. ————— 96. ————— 97. Постоянная величина – величина имеющая в данных условиях неизменное значение Переменная – величина, которая в данных условиях в результате его изменения может принимать разные значения Если величина сохраняет постоянное значение лишь в условиях данного процесса, она называется параметром. 98. Абсолютная величина(или модулем) действительного числа Xназывается само число X, если Xнеотрицательно, и противоположно –Xесли X отрицательно. Модуль числа Zможно рассматривать как расстояние от начало координат до точки, составляющее значение выражения внутри модуля. 99. Всякий интервал содержащий точку a называется окрестностью точки а Интервал(а-E, a+E)т.е. множество точек X таких что [x-a]<E,называется Е окрестностью точки а 100. ООФ - такое множество значений аргументаX, при котором ф-ия существует. ОЗФ- множество значений самой функции сущ. , имеет смысл, её можно сосчитать Способы: Аналитический, табличный, графический, словесны 101. Четная функция – функция , что выполняет условие f(x)=f(-x) для любой точки из области определения. Нечетная функция – функция , что выполняет условие-f(x)=f(-x) Периодическая ф-ияфункция которая повторяет свои значения через какой-то определенный интервал 102. Ф-ия называется возрастающей если (убывающей) если большему значению аргумента из этого промежутка соответствует большему(меньшему) значению ф-ии Возрастающие и убывающие ф-ии называются монотонными Ф-ия называется ограниченной на промежутке X если сущ. такое положительное число М, что [f(x)]<= М для любого X 103. Смотреть приложение 104. Смотреть приложение 105. Смотреть приложение 106. Смотреть приложение 107. Если функция f (х) задает взаимно однозначное соответствие между своей областью определения X и своей областью значений Y, то говорят, что функция f (х) имеет обратную функциюили что функция f (х) обратима. Обратная функция, по определению, — это правило, которое каждому числу y ∈ Y сопоставляет число х ∈ X, причем y = f (х). Некоторые свойства взаимно обратных функций. 1) Тождества. Пусть f и g – взаимно обратные функции. Это означает, что равенства y = f(x) и x = g(y) равносильны. Подставим одно из этих равенств в другое. Получим два тождества f(g(y)) = yи g(f(x)) = x. 2) Область определения. Пусть f и g – взаимно обратные функции. Область определения функции f совпадает с областью значений функции g, и наоборот, область значений функции f совпадает с область определения функции g. 3) Монотонность. Если одна из взаимно обратных функций возрастает, то и другая возрастает. Аналогичное верно и для убывающих функций. 4) Графики. Графики взаимно обратных функций, построенные в одной и той же системе координат, симметричны друг другу относительно прямой y = x. 108. ————— 109. Функция называется бесконечно малой в точке если 110. Свойства бесконечно малых функций Пусть α(x) и β(x) — бесконечно малые функции при x → x0, и f(x) ограничена в некоторой проколотой окрестности точки x0. Тогдаα(x) + β(x) — бесконечно малая функция при x → x0; α(x) · f(x) — бесконечно малая функция при x → x0. 111. ————— 112. ————— 113. ————— 114. ————— 115. Основные свойства 1.Предел суммы Предел суммы равен сумме пределов, если каждый из них существует, т.е. 2.Предел разности Предел разности равен разности пределов, если каждый из них существует, т.е. 3.Предел постоянной величины Предел постоянной величины равен самой постоянной величине: 4.Предел произведения функции на постоянную величину Постоянный коэффициэнт можно выносить за знак предела: 5 .Предел произведения Предел произведения равен произведению пределов, если каждый из них существует, т.е. 6.Предел частного Предел частного равен частному пределов, если каждый из них существует и знаменатель не обращается в нуль, т.е. 7.Предел степенной функции где степень p - действительное число. 8.Предел показательной функции где основание b > 0. 9.Предел логарифмической функции где основание b > 0. 116. 1.ноль на ноль способы решения: правила Лопиталя, выделение сомножителя, использование первого замечательного предела 2.бесканечность на бесконечность способы решения, Лопиталя, выделение старшой степени, избавление от иррациональности 117. первый замечательный предел 118. второй замечательный предел 119. и 1. Если =А¹ 0 (АєR), то α и ß называются бесконечно малыми одного порядка. 2. Если, =0, то α називатся бесконечно малой более высокого порядка , чем ß. 3. Если =∞, то α называется бесконечно малой более низкого порядка, чем ß. 4. Если не существует, то α и ß называются несравнимыми бесконечно малыми. 120. Функция f(x) называется непрерывной в точке x0 если сущ. limx→x0f(x)= значению ф-ии в этой точке, условие limx→x0f(x)=f(x0)Левосторонний и правосторонний пердел ф-ии это пределы числовой ф-ии подразумевающий «приближение » и предельности точки с одной стороны 121. Сложной функцией называется ф-иязначение которой вычисляют по правилу h(x)=f’(g(x)) то есть сначала вычисляется g(x) при этом получается некоторое число Y а затем вычисляется значение в точке Y 122. ————— 123. Среди значений которые ф-ия принимает в точках данного промежутка, имеются самое большое и самое малое 124. Точка называется первого рода если limx→a-0f(x)=limx→a+0f(x) - точка устранимого разрыва Если limx→a-0f(x)≠limx→a+0f(x) точка конечного разрыва Точка разрыва второго порядка это когда один из односторонних пределов = ∞ или не сущ. 125. Ф-ия называется явной если в её правой части нет Y пример y=x2+2x+5 Ф-ия называется не явной если она задана уравнением вида F(x,y)=0, не разрешенным относительно зависимой переменной 126. ————— 127. ————— 128. 1.Задача о скорости движущейся точки 2.Задача показательной к данной кривой 129. Если существует предел отношения приращения ф-ии∆y=f(x0+∆x)-f(x0) к вызвавшему его приращение аргумента ∆x когда ∆x=> 0, то это производная. Обозначение f’(x0); y’x;y’(x0) 130. Непрерывная ф-ия имеет в точке конечную производную тогда и только тогда, когда её график в точке имеет касательную с угловым коэффициентам 131. Если положение точки при её движение по числовой прямой задается ф-ияS=f(t); где t- время движения от производной ф-ии, S- мгновенная скорость движения в момент времени t 132. ————— 133. Если ф-ия дифференцируема, то она явл. непрерывной , но если ф-ия непрерывна, то это не значить что она дифференцируема 134. Y=f(x0)+f`(x0)*(x-x0) уравнение касательной Y=-1/f`(x0)+(x-x0)+f(x0) уравнение нормали 135. 1. Производная постоянной =0 2.производная аргумента=1 3.произвондая от корня квадратного= ½ самого квадратного корня 136. (xa)’=axa-1степенная (ax)’=axlnaпоказательная (Logax)’=1/x*lnaлогорифмическая 137. 138. (f(x)+(-)g(x))’=f’(x)+(-)g’(x) (f(x)*g(x))’=f’(x)*g(x)+f(x)*g’(x) (f(x)/g(x))’=(f’(x)*g(x)-f(x)*g’(x))/(g(x))2 139. Производная сложной ф-ииy’=y’(x)*(x)’ 140. 1. Логарифмируем обе части уравнения, по уравнению записи ф-ии и используем св-ва логарифма :lny=lnUv=>lny=v*lnU 2. находим производные от левой и правой частей уравнения, при этом учитывается что Yзависит от X , т.е. слева находят производную от сложной ф-ии, а справа как от произведения. 3.умнажаем все уравнение на Y 4. вместо Y подставляем исходное выражение 141. 142. В начале дифференцируем функцию по отношению к аргументу(x), а затем берем производную как от сложной функции. 143. Суть параметрического представления ф-ии дает такое важное преимущество что позволяет изучать неявные ф-ии в тех случаях , когда их приведение к неявному виду затруднительно. 144. Производные порядка выше первого называются производными высших порядков.

Механический смысл производной второго порядка

Пусть материальная точка М движется прямолинейно по закону S=f(t). Как уже известно, производная S _t равна скорости точки в данный момент времени: S'_t=V.

Покажем, что вторая производная от пути по времени есть величина, ускорения прямолинейного движения точки, т. е. S"=α.

Пусть в момент времени t скорость точки равна V, а в момент t+∆t — скорость равна V+∆V, т. е. за промежуток времени ∆t скорость изменилась на величину ∆V.

Отношение ∆V/∆t выражает среднее ускорение движения точки за время ∆t. Предел этого отношения при ∆t→0 называется ускорением точки М в данный момент t и обозначается буквой α: 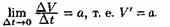Но V=S'_t. Поэтому α=(S'_t)', т. е. α=S'_t'

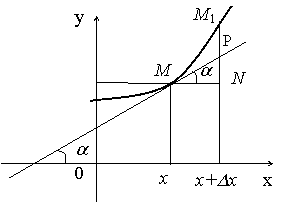
145. На графике функции 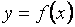возьмем произвольную точку 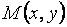и дадим аргументу 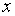приращение 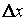. При этом функция получит приращение 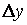(на рисунке отрезок ).

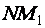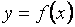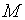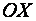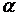Проведем касательную к кривой в точке и обозначим угол ее наклона к оси через , тогда 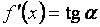. Из треугольника 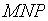находим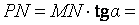 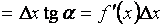, т.е. .

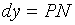Таким образом, дифференциал функции численно равен приращению ординаты касательной, проведенной к графику функции 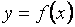в данной точке, когда аргумент 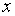получает приращение .

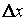146. Применение дифференциала к приближенным вычислениям.

Дифференциал функции y = f(x) зависит от х и является главной частью приращения х.

Также можно воспользоваться формулой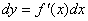

Тогда абсолютная погрешность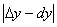

Относительная погрешность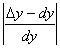

147. —————

148. Теорема ЛагранжПусть функция 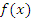дифференцируема в открытом промежутке 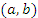и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка 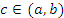, что

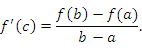
149. Теорема (правило Лопиталя) Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть 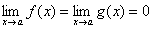или 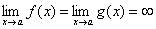. Тогда, если существует предел отношения производных этих функций 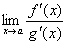, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

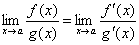
(1)

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных. Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа,

150. К критическим точкам относятся те точки, в которых производная = 0 и в которых она не существует.
Функция называется возрастающей, если для любой пары значений аргументов и из неравенства следует неравенство .
Функция называется убывающей, если для любой пары значений аргументов и из неравенства следует неравенство .
Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке. Достаточные признаки монотонности функции: Если f ’( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале. Если f ’( x ) < 0 в каждой точке интервала ( a, b ) , то функция f ( x ) убывает на этом интервале.

151. Необходимое условие экстремума. Во всех точках экстремума производная функции не существует или равна нулю.

152. Удобно пользоваться упрощенной формулировкой этого признака: если в точке х0 производная меняет знак с плюса на минус, то хо есть точка максимума.

153. если в точке 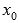функция непрерывна и в ней производная меняет знак с минуса на плюс, то 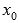- точка минимума.

154. Если х 0 есть стационарная точка функции f(x) и f’’(x)<0, то в точке х 0 функция имеет максимум,а если f’’(x)>0 , то функция имеет в точке х 0 минимум.

155.

156. Алгоритм.

Находим область определения функции.

Находим производную функции на области определения.

Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (эти точки называютточками возможного экстремума, проходя через эти точки, производная как раз может изменять свой знак).

Эти точки разбивают область определения функции на промежутки, в которых производная сохраняет знак. Определяем знаки производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала).

Выбираем точки, в которых функция непрерывна и, проходя через которые, производная меняет знак.

157. Алгоритм:

найти ;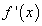

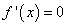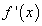найти точки, в которых или не существует, и отобрать из них те, что лежат внутри отрезка ;

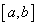вычислить значения функции 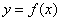в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции 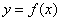на отрезке 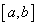, которые можно обозначить так: .

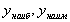158. Критической точкой (по второй производной) называется точка, в которой вторая производная равна нулю или не существует.

159. Доказательство. Пусть, например, 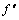(х)< 0 в интервале (х0-; х0) и 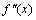> 0 в интервале (х0; х0+), где  – положительное число. В этом случае график функции в интервале (х0–ε; х0) выпуклый, а в интервале (х0; х0+ε) – вогнутый. Следовательно, точка (х0;f(х0)) по определению является точкой перегиба.

160. Асимптотой функции называют прямую, к которой приближаются точки графика функции при бесконечном удалении их от начала координат.

161. —————

162. 1) найти область определения и область значений функции;
2) установить, является ли функция чётной или нечётной;
3) определить, является ли функция периодической или нет;
4) найти нули функции и её значения при ,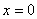
5) найти интервалы знаков постоянства;
6) найти интервалы монотонности;
7) найти точки экстремума и значения функции в этих точках;
8) проанализировать поведение функции вблизи “особых” точек и при больших значениях модуля x.

Дата добавления: 2018-08-06; просмотров: 353; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!