Построение КЭ соотношений из принципа возможных перемещений
Цель данных преобразований состоит в том, чтобы записать уравнения равновесия системы через узловые неизвестные конечно-элементной сетки.
Принцип возможных перемещений состоит в том, что для тела находящегося в состоянии равновесия и получившего в этом состоянии бесконечно малое возможное смещение точек, работа внутренних сил на возможное перемещение точек равна работе внешних сил на эти возможные перемещения.
Выберем из модели отдельный конечный элемент с номером «е» и применим к нему принцип (рис. 3).
Рис. 3. Конечный элемент
Рассмотрим работу внешних сил на возможное перемещение:
.
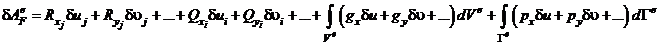
Здесь 
– вариация вектора перемещений 
.
Мы знаем, что 
(так как 
) и 
. Тогда
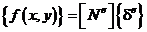или
,
где 
– вектор-столбец узловых сил конечного элемента, вызванных действием объемных усилий;
– вектор-столбец узловых сил конечного элемента, вызванных действием распределенной нагрузки.
Это была работа внешних сил на возможных перемещениях.
, где 
.
Теперь работа внутренних упругих сил:
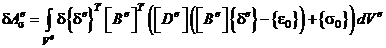
или
,
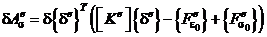где 
– матрица жёсткости конечного элемента (квадратная, симметричная, положительно определённая;
– узловые силы от действия свободных деформаций;
– узловые силы от действия начальных напряжений.
Зная, что 
, получаем
, следовательно
Очевидно –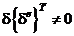 
! Тогда выражение в скобках равно нулю.
Обозначим 
, тогда
или 
, откуда
.
Записывая условия равновесия 
-го узла всей системы КЭ имеем
|
|
|
, 
. Тогда 
по всем элементам!
или для всей системы 
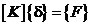– СЛАУ МКЭ (состоит из глобальной матрицы и векторов)!
Это и есть жёсткостная форма записи МКЭ. Для решения необходимо учесть кинематические ГУ, иначе система будет иметь нулевой определитель!
Рассмотрим применение метода конечных элементов на примере задачи линейной теории упругости в перемещениях.
Одномерный конечный элемент
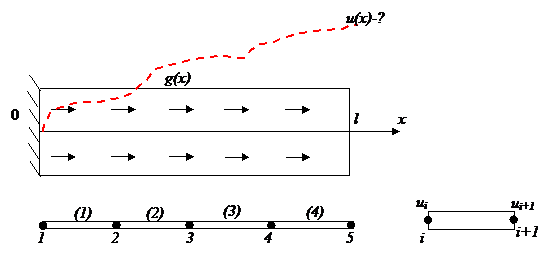
Рис. 4. Расчетная схема
-перемещение в любой точке конечного элемента.
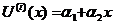
-функции формы конечного элемента.
Вводим локальную координату 
, которая изменяется от 0 до 1.
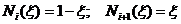- функции формы в локальной системе координат.
Введем во всей области изменения аргумента от 0 до 
следующие аппроксимирующие функции:
- перемещение.
Воспользуемся принципом минимума потенциальной энергии: из всех кинематически возможных полей перемещений в действительности реализуются те, которые доставляют минимальное значение потенциальной энергии системы.
- потенциальная энергия упругой деформации, 
- потенциальная энергия внешних сил.
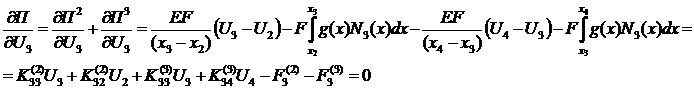
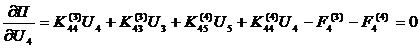
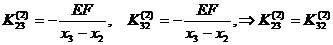
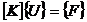, где 
- глобальная матрица жесткости системы конечных элементов,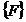 
- глобальный вектор сил системы конечных элементов.
|
|
|
Важно то, что элементы глобальной матрицы жесткости и элементы глобального вектора сил формируются суммированием соответствующих элементов матриц жесткости и векторов сил отдельных конечных элементов.
Особенности матрицы жесткости:
· имеет ленточную структуру
· обладает симметрией относительно главной диагонали
Дата добавления: 2018-08-06; просмотров: 214; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!