Порядок выполнения коллоквиума
Коллоквиум
Теоретические сведения
Вычисление значения 
с заданной точностью методом прямоугольников
Для вычисления значения определённого интеграла функции, монотонной и непрерывной на конечном отрезке [a,b], можно воспользоваться методом прямоугольников. Для вычисления первого приближения интеграла разделим отрезок [a,b], отвечающий пределам интегрирования (рис.1), на n равных частей (n = 4), определим значения
xi = a+h*i-h/2;
h = (b-a)/n.
Вычислим площадь одного прямоугольника si=h*f(xi). Сумма si 
площадей полученных прямоугольников является приближенным значением интеграла: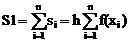 
.
Однако одно приближение не позволяет оценить точность, с которой вычислено значение интеграла, необходимо найти следующее приближение. Для этого увеличим n в два раза, т.е. n = 2n. Аналогично найдем 
.
Рис.1 Вычисление интеграла методом прямоугольников
Требуется вычислить значение интеграла с точностью e, поэтому проверим условие |S1 - S2|<e. Если условие выполняется, то S2 принимается за искомое значение интеграла; если не выполняется, то последнее выполненное значение S2 считается предыдущим, т.е. S1 = S2. После этого удвоим число точек деления отрезка и вычислим новое значение S2. Процесс удвоения n и вычисления S2 будем продолжать до тех пор, пока модуль разности S1 и S2 не станет меньше e.
Пример 1.Вычисление интеграла 
методом прямоугольников.
#include <iostream.h>
|
|
|
#include <conio.h>
#include <math.h>
#define Pi 3.14159
int main()
{unsigned long i, n = 4;
float a,b,x,h,S1,S2,eps,exact;
a = 0; b = 3/(2*Pi); eps = 0.001;
S1 = 0;
h = (b – a)/n;
//Вычисляем сумму в первом приближении
for (i = 1; i<=n; i++)
{ x = a + i*h – h/2;
S1 = S1+ (1/(5–3*cos(x)))*h;
}
//Вычисляем текущее приближение и сравниваем его с предыдущим
do {n = 2*n;
h = (b – a)/n;
S2 = 0;
for (i = 1; i<=n; i++)
{x = a + i*h – h/2;
S2 = S2 + (1/(5–3*cos(x)))*h;
}
exact = fabs(S1 – S2);
S1 = S2;
} while(exact>eps);
cout << "S = " << S2) ;
return 0;
}
Решение уравнения f(x) = 0 с заданной точностью e
Методом деления отрезка пополам
Для решения уравнения 
на отрезке 
, где 
непрерывная функция, меняющая знак на отрезке, можно применять метод деления отрезка пополам. Метод деления отрезка пополам заключается в следующем. Проверяется перемена знака функцией на отрезке [a,b] (рис.2).
Рис.2. Метод деления отрезка пополам.
Для этого вычисляются значения функций f(a) и f(b). Если f(a)*f(b)>0, то этот метод не приводит к желаемому результату. Если f(a)*f(b)<0, т.е. на концах отрезка [a,b] функция f(x) имеет противоположные знаки, то поиск корня происходит следующим образом. Находим в точке a значение функции y1 = f(a). Затем определяем значение 
и вычисляем значения y2 = f(х). Теперь, если f(a)*f(х)>0, то корень находится на отрезке [x,b], если f(a)*f(x)£0, то корень находится на отрезке [a,x]. В первом случае перемещаем точку а вправо, выполняя присваивание а = х, во втором случае перемещаем b влево, b=x. Таким образом, получаем второй отрезок [a,b], но вдвое меньший предыдущего. Процесс деления отрезка пополам продолжаем до тех пор, пока отрезок [a,b] не станет меньше заданной точности. После этого вычисляем значение x = (a+b)/2.
|
|
|
Пример 2.Решение уравнения 
с заданной точностью e = 0.01 методом деления отрезка пополам, если корень находится на отрезке [1,3].
#include <iostream.h>
#include <conio.h>
main()
{ int n = 0;
float x, a = 1, b = 3, y1, y2, eps = 0.001, e, r, l;
l = a; r = b;
y1 = a*a*a – 2*a*a – 3;
y2 = b*b*b – 2*b*b – 3;
if (y1*y2>0) { cout << "Корней нет" <<endl;
getch();
exit(1) ;
}
do { ++n;
x = (a+b)/2;
y1 = a*a*a – 2*a*a – 3;
y2 = x*x*x – 2*x*x – 3;
if (y1*y2>0) a = x;
else b = x;
} while (b – a)>eps;
x = (a + b)/2;
cout << "Корень уравнения на отрезке "<< l << ", " << r << "равен " << x << " и получен за " << n <<"шагов";
cout << endl;
return 0;
}
Контрольные вопросы
|
|
|
1. Каким образом цикл whileможет имитировать цикл for?
2. Каким образом цикл whileможет имитировать цикл do-while?
3. В каких случаях используются операторыbreak, gotoиcontinueи функцияexit()?
Порядок выполнения коллоквиума
1. Получить от преподавателя номер варианта.
2. Ознакомиться с данным описанием и составить программу, указанную в задании.
3. Подготовить файл с программой и отладить её. Результаты показать преподавателю.
4. Оформить отчет.
Лабораторное задание
1. Для своего варианта cоставить программу вычисления суммы бесконечного ряда c точностью, значение которой ввести с клавиатуры задание 1.
2. Реализовать указанные в задании 2 методы, согласно номеру своего варианта.
Требования к отчету
Отчет должен содержать:
1) название и цель работы;
2) схему алгоритма;
3) краткие теоретические сведения;
4) текст программы для варианта задания, полученного от преподавателя;
5) результаты выполнения программ.
Варианты заданий
Задание 1
Ввести с клавиатуры х и точность вычисления Eps. Вычислить с заданной точностью сумму
| Номер варианта | Задание |
| 1, 16 |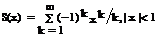 
|
| 2, 17 |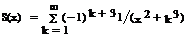 
|
| 3, 18 | 
|
| 4, 19 | 
|
| 5, 20 | 
|
| 6, 21 | 
|
| 7, 22 | 
|
| 8, 23 | 
|
| 9, 24 | 
|
| 10, 25 | 
|
| 11, 26 |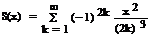 
|
| 12, 27 | 
|
| 13, 28 | 
|
| 14, 29 | 
|
| 15, 30 | 
|
|
|
|
Задание 2
| Номер варианта | Задание |
| 1, 16 | Методом деления отрезка пополам найти приближенное значение корня уравнения x + ln(x + 0.5) – 0.5 = 0 на интервале [0,2]. Абсолютная погрешность не превышает  .
|
| 2, 17 | Методом деления отрезка пополам найти приближенное значение корня уравнения 2x3 + 4x – 1 = 0 на интервале [0,0.5]. Абсолютная погрешность не превышает  .
|
| 3, 18 | Методом деления отрезка пополам найти приближенное значение корня уравнения 1/x = sin x на интервале [0,2]. Абсолютная погрешность не превышает .
|
| 4, 19 | Методом прямоугольников вычислить приближенное значение интеграла  . Абсолютная погрешность не превышает 0.001.
|
| 5, 20 | Методом деления отрезка пополам найти приближенное значение корня уравнения x4 + 2x3 – x – 1 = 0 на интервале [0,1]. Абсолютная погрешность не превышает 0.00015. |
| 6, 21 | Методом деления отрезка пополам найти приближенное значение корня уравнения x3 + 12x – 2 = 0 на интервале [0.5,1]. Абсолютная погрешность не превышает 0.00015. |
| 7, 22 | Методом прямоугольников вычислить приближенное значение интеграла  . Абсолютная погрешность не превышает 0.001.
|
| 8, 23 | Методом деления отрезка пополам найти приближенное значение корня уравнения x5 – x – 0.2 = 0 на интервале [0.9,1.1]. Абсолютная погрешность не превышает 0.0001. |
| 9, 24 | Методом деления отрезка пополам найти приближенное значение корня уравнения 5x + 8lnx – 1 = 0 на интервале [4,5]. Абсолютная погрешность не превышает 0.0015. |
| 10, 25 | Методом прямоугольников вычислить приближенное значение интеграла  Абсолютная погрешность не превышает 0.001.
|
| 11, 26 | Методом деления отрезка пополам найти приближенное значение корня уравненияx3 – 2x2 + x – 3 = 0 на интервале [2.1,2.2]. Абсолютная погрешность не превышает 0.001. |
| 12, 27 | Методом деления отрезка пополам найти приближенное значение корня уравнения x3 + x2 – 3 = 0 на интервале [0.5,1.5]. Абсолютная погрешность не превышает 0.00001. |
Дата добавления: 2018-08-06; просмотров: 119; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!