Правила вычисления производной алгебраической суммы, произведения и частного
Глава III. Дифференциальное исчисление функции одной переменной
§7. Производная
1. Определение производной
Рассмотрим следующие задачи, приводящие к пониманию производной.
1) Проведение касательной к кривой на плоскости
Пусть на плоскости β дана некоторая непрерывная кривая L. Возьмем на ней некоторую фиксированную точку М0. Если М1≠М0, М1 ∋ L 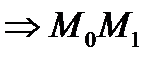 - секущая. Будем перемещать М1 вдоль L так, чтобы М1 стремилась к совпадению с М0. Секущая будет менять свое положение в зависимости от положения М1. Предельное положение секущей М0М1 (если оно существует) при М1→М0 называется касательной к кривой L в точке М0.
- секущая. Будем перемещать М1 вдоль L так, чтобы М1 стремилась к совпадению с М0. Секущая будет менять свое положение в зависимости от положения М1. Предельное положение секущей М0М1 (если оно существует) при М1→М0 называется касательной к кривой L в точке М0.
Пусть кривая L задана в системе координат хОу уравнением 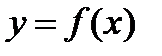
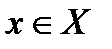 .
. 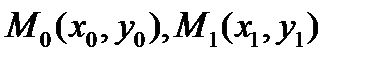 .
.
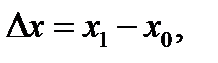
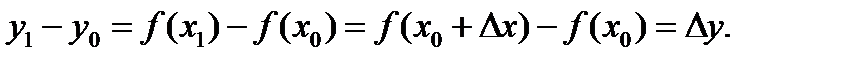
Найдем угловой коэффициент секущей М0М1: из ∆М0КМ1: 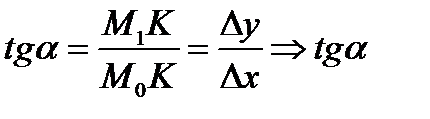 зависит только от ∆х. Т.к. М1→М0
зависит только от ∆х. Т.к. М1→М0  ~ ∆х→0, угловой коэффициент касательной, проведенной к кривой L в точке М0(х0,у0), получим предельным переходом при ∆х→0, т.е.
~ ∆х→0, угловой коэффициент касательной, проведенной к кривой L в точке М0(х0,у0), получим предельным переходом при ∆х→0, т.е. 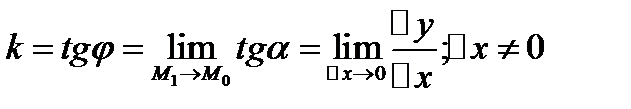 , если этот предел существует и конечен.
, если этот предел существует и конечен.
2) Нахождение мгновенной скорости прямолинейно движущейся точки
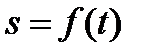 - уравнение движения точки и
- уравнение движения точки и 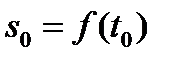 - путь, пройденный точкой до фиксированного момента
- путь, пройденный точкой до фиксированного момента 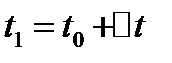 . Найдем путь, пройденный точкой за время
. Найдем путь, пройденный точкой за время 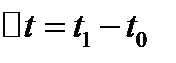 :
: 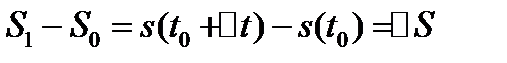 .
.
Средней скоростью ϑср прямолинейного движения за время ∆t наз-ся отношение пройденного пути к затраченному времени: 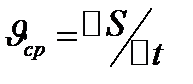 . Если существует предел ϑср при ∆t→0, он называется мгновенной скоростью в момент t0:
. Если существует предел ϑср при ∆t→0, он называется мгновенной скоростью в момент t0: 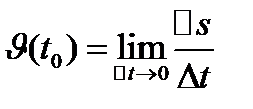 .
.
3) Нахождение производительности труда
|
|
|
Пусть известна функция u=u(t), выражающая количество произведенной продукции и за время работы t. Вычислим количество произведенной продукции за время 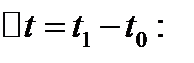
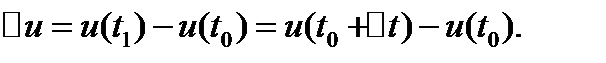
Средней производительностью труда называется отношение количества произведенной продукции к затраченному времени, т.е. 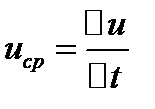 .
.
Производительностью труда рабочего 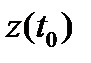 в момент t0 называется предел, к которому стремится zcp при
в момент t0 называется предел, к которому стремится zcp при 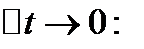
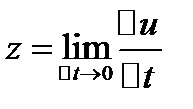 .
.
Сопоставляя рассмотренные задачи, видим, что во всех случаях выполняются аналогичные действия. Дадим опр-е производной.
Опр.7.1: Пусть дана функция 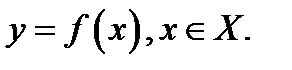 Выберем некоторую точку х0∈Х и найдем
Выберем некоторую точку х0∈Х и найдем 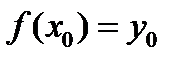 . Дадим х0 приращение
. Дадим х0 приращение 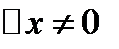 так, чтобы
так, чтобы 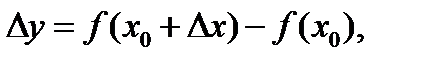 которое зависит только от ∆х. Найдем отношение ∆у/∆х. Перейдем к пределу при ∆х→0, т.е. найдем
которое зависит только от ∆х. Найдем отношение ∆у/∆х. Перейдем к пределу при ∆х→0, т.е. найдем 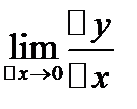 . Если этот предел отношения приращения функции ∆у к соответствующему приращению аргумента ∆х при ∆х→0, (∆х≠0) ∃ и конечен, он называется производной функции
. Если этот предел отношения приращения функции ∆у к соответствующему приращению аргумента ∆х при ∆х→0, (∆х≠0) ∃ и конечен, он называется производной функции 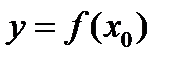 в точке х0.
в точке х0.
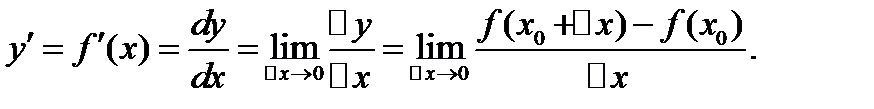
Т.о., в задаче (1) нахождения условного коэффициента касательной к кривой 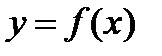 в точке М0(х0,у0) сводится к нахождению
в точке М0(х0,у0) сводится к нахождению 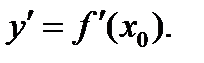
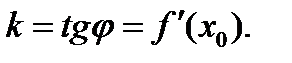
Получили геометрический смысл производной: угловой коэффициент 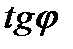 касательной в точке х=х0 есть производная ф-ии у по аргументу х.
касательной в точке х=х0 есть производная ф-ии у по аргументу х.
Из (2) задачи следует механический смысл производной: мгновенная скорость 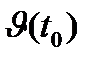 в момент времени t0 есть производная ф-ии пути по времени
в момент времени t0 есть производная ф-ии пути по времени 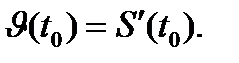
|
|
|
В (3) задаче вычисление производной производительности труда рабочего в момент времени t0 сводится к вычислению производной ф-ии кол-ва произведенной продукции по времени: 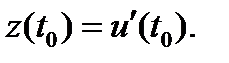
Пример: Найти производные:
1) 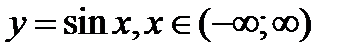 . Для ∆х≠0
. Для ∆х≠0
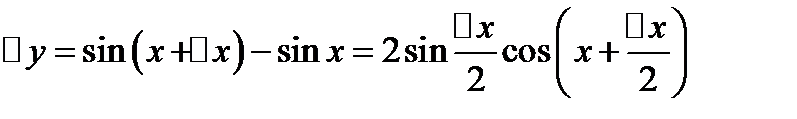
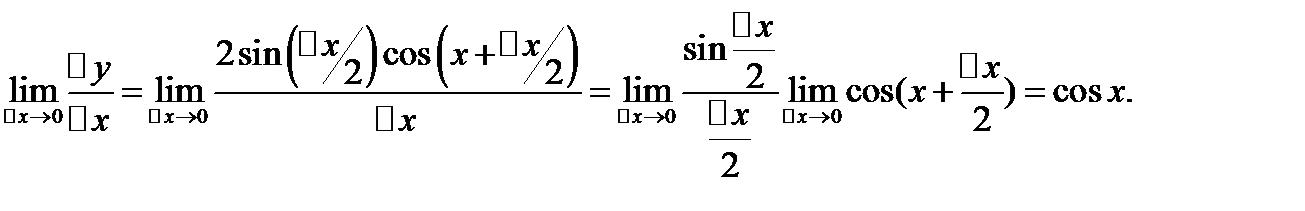
2) 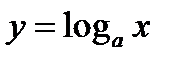
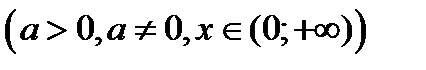
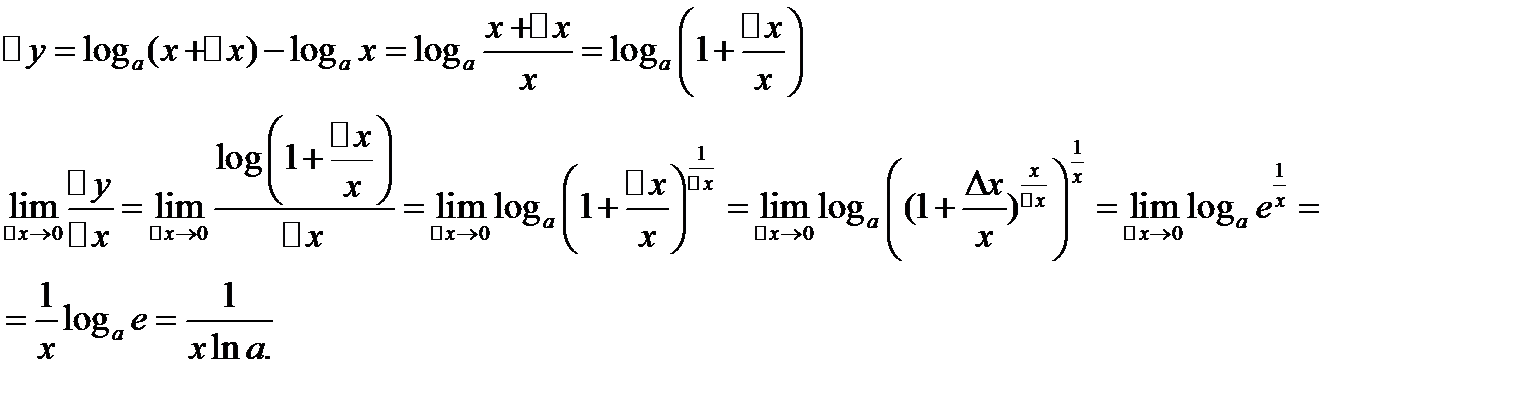
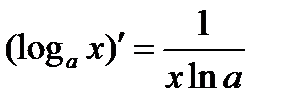 ;
; 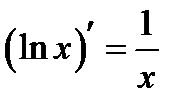 ;
; 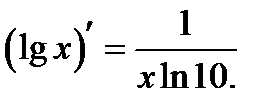
Т.о., значение производной состоит в том, что при изучении любых процессов и явлений природы с ее помощью можно оценить скорость изменения связанных между собой величин.
2. Понятие дифференцируемости функции
Опр.7.2: Функция 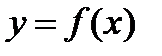 называется дифференцируемой в точке х0, если ее приращение ∆у в этой точке можно представить в виде
называется дифференцируемой в точке х0, если ее приращение ∆у в этой точке можно представить в виде 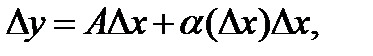 (*) где
(*) где 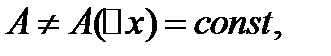
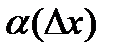 - б.м. при
- б.м. при 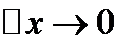 , т.е.
, т.е. 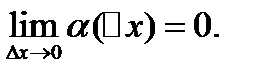
Теорема 7.1: (Необходимое и достаточное условие дифференцируемости функции)
Для того, чтобы функция 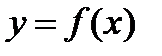 была дифференцируема в точке х0
была дифференцируема в точке х0 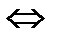 чтобы она имела в этой точке конечную производную.
чтобы она имела в этой точке конечную производную.
Т.о., для функций одной переменной дифференцируемость и существование производной – равносильные понятия, поэтому операцию нахождения производной называют дифференцированием.
Теорема 7.2: (связь дифференцируемости и непрерывности функции)
Если функция 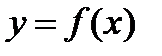 определена на Х и в точке х0∈Х имеет конечную производную
определена на Х и в точке х0∈Х имеет конечную производную 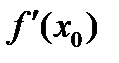 , то
, то 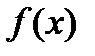 непрерывна в точке х0.
непрерывна в точке х0.
|
|
|
Следствие: в точках разрыва функции 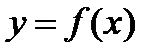 производная не существует.
производная не существует.
3. Односторонние и бесконечные производные
В определении производной предполагалось, что предел 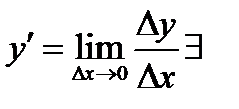 и конечен. Но эти условия не всегда выполняются. Предел в некоторых точках может не существовать, а может быть бесконечным.
и конечен. Но эти условия не всегда выполняются. Предел в некоторых точках может не существовать, а может быть бесконечным.
Определение 7.3
Односторонними производными называется 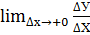 и
и 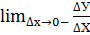 если они существуют. По аналогии с односторонними пределами их называют правой и левой производными и обозначают соответственно f’(x0+0) и f’(x0-0).
если они существуют. По аналогии с односторонними пределами их называют правой и левой производными и обозначают соответственно f’(x0+0) и f’(x0-0).
Очевидно, что если в точке х0 существует производная, то существует и односторонние производные и они равны между собой.
Определение 7.4
Если 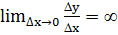 , то производная называется бесконечной
, то производная называется бесконечной
n-4.Производная сложной и обратной функции
Теорема 7.3 (производная сложной функции). Если функция u= 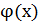 имеет в некоторой точке х0 производную
имеет в некоторой точке х0 производную 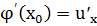 , а функция у=f(u) имеет в соответствующей точке u0=
, а функция у=f(u) имеет в соответствующей точке u0= 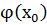 производную
производную 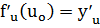 , то сложная функция y=f(
, то сложная функция y=f( 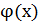 ) имеет производную
) имеет производную 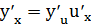 в точке х0
в точке х0
Теорема 7.4 (производная обратной функции)
Пусть функция y=f(x) удовлетворяет условиям теоремы о существовании обратной функции и в точке х0 имеет обратную производную f’(x0) 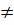 0. Тогда обратная функция x=g(y) в точке у0 также имеет конечную производную, равную
0. Тогда обратная функция x=g(y) в точке у0 также имеет конечную производную, равную 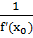 .
.
|
|
|
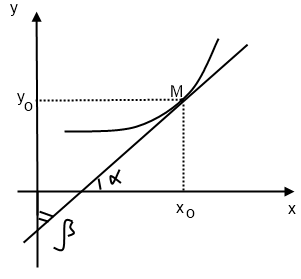
Эта теорема имеет следующий геометрический смысл. Рассмотрим в некоторой окрестности точки х0 произвольную y=f(x) (или обратную функции x=g(y)). Пусть точке х0 на этом графике соответствует точка M. f’(x0)=tg 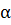 , т.е. tg
, т.е. tg 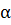 угла наклона касательной, проходящей между точкой М, к оси Ох. Производная обратной функции g’(y0) равна tg
угла наклона касательной, проходящей между точкой М, к оси Ох. Производная обратной функции g’(y0) равна tg 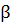 угла наклона той же касательной к оси Оу. Т.к.
угла наклона той же касательной к оси Оу. Т.к. 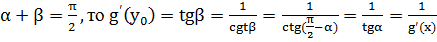 .
.
Правила вычисления производной алгебраической суммы, произведения и частного
1) Пусть функция y=f(x) имеет производную y’ в точке х0,тогда функция u=cy, c=const имеет производную в точке х0, а именно: u’=cy’
2) Пусть функции u= 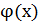 и v=f(x) имеют в точке конечные производные u’(x0) и v’(x0), тогда функцияy=u
и v=f(x) имеют в точке конечные производные u’(x0) и v’(x0), тогда функцияy=u 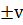 имеет в точке х0 производную y’=u’
имеет в точке х0 производную y’=u’ 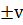 ’.
’.
3) Пусть функции uи vимеют в точке х0 конечные производные u’(x0), v’(x0) и y=uv. Тогда существует производная y’(x0) и y’=u’v+v’u
4) Пусть u и v имеют в точке х0 конечные производные u’(x0), v’(x0) 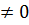 , y=
, y=  , тогда существует y’(x0) иy’=
, тогда существует y’(x0) иy’= 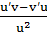 .
.
5) Логарифмическая производная
Пусть даны функции u= 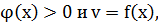 определены на Х и имеющие производные u’(x0) и v’(x0) в точке х0
определены на Х и имеющие производные u’(x0) и v’(x0) в точке х0 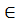 Х, тогда сложная функция y=(
Х, тогда сложная функция y=( 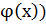 f(x)тоже имеет производную. Т.к.
f(x)тоже имеет производную. Т.к. 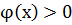 по условию, y можно прологарифмировать lny=f(x)ln
по условию, y можно прологарифмировать lny=f(x)ln 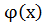 . Дифференцируя и приравнивая части получим
. Дифференцируя и приравнивая части получим
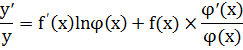
Дифференциал
n-1. Определение и геометрический смысл дифференциала
Определение 8.1. Пусть дана функция y=f(x), определенная на множестве Х, и в точке х0 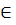 Х существует y’(x0). Тогда по определению производной
Х существует y’(x0). Тогда по определению производной 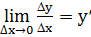 , а по определению предела
, а по определению предела 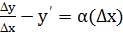 ,
, 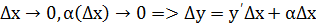
Если  y можно представить в виде
y можно представить в виде  y=А
y=А  x+
x+ 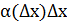 , где А
, где А 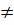 0, то величина А
0, то величина А 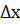 , линейная относительно
, линейная относительно 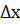 ,называется дифференциалом функции y=f(x) в точке х0, т.е. dy=A
,называется дифференциалом функции y=f(x) в точке х0, т.е. dy=A 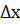 . Если А существует, то функция называется дифференцируемой.
. Если А существует, то функция называется дифференцируемой.
Определение 8.2
Любое приращение 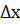 такое, что (х+
такое, что (х+ 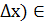 Х, принимается за дифференциал независимой переменной, тогда
Х, принимается за дифференциал независимой переменной, тогда 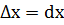
Таким образом, dy=Adx 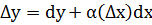
Определение 8.3
Если 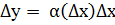 , т.е. А=0, то будем считать, что дифференциал существует и dy=0. В этом случае f’(x0)=0 и функция дифференцируема. Таким образом dy=
, т.е. А=0, то будем считать, что дифференциал существует и dy=0. В этом случае f’(x0)=0 и функция дифференцируема. Таким образом dy= 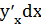 =f’(x0)dx
=f’(x0)dx
Если функция y=f(x) дифференцируема, то dy и 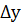 –б.м. при
–б.м. при 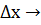 0
0
Определение 8.4
Дифференциалом dy функции y=f(x) называется главная, линейная относительно 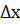 , часть приращений функции А
, часть приращений функции А 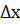 при А
при А 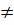 0, т.е. dy=Adx и dy=0 при А=0.
0, т.е. dy=Adx и dy=0 при А=0.
Рассмотрим геометрический смысл дифференциала
Пусть кривая L задана уравнением y=f(x) и функция y=f(x) в точке х0 имеет конечную производную y’=f’(x0). К кривой Lчерез точку M0 (x0,y0) проведем касательную М0Т, которая в этом случае существует.
Дадим аргументу х приращение 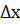 =dx, найдем
=dx, найдем 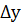 и возьмем точку M1 (х0+
и возьмем точку M1 (х0+ 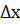 ,у0+
,у0+ 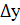 ). Из
). Из 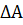 M0B:
M0B:
АВ=АМ0tg 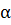 =
= 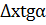 =y’
=y’ 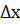 =dy
=dy
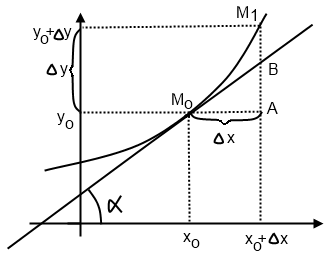
Дифференциал функции в точке х0 – это приращение ординаты касательной к кривой в этой точке.
Таким образом, y’= 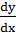 , т.е. производная – это отношение дифференциала ыункци к дифференциалу аргумента. dy зависит от dxи изменяется пропорционально ему, y’(x) – коэффициент пропорциональности.
, т.е. производная – это отношение дифференциала ыункци к дифференциалу аргумента. dy зависит от dxи изменяется пропорционально ему, y’(x) – коэффициент пропорциональности.
Пусть y=f(x), x 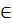 X, dy=y’(x)dx. Рассмотрим сложную функцию y=F(x)=f(
X, dy=y’(x)dx. Рассмотрим сложную функцию y=F(x)=f( 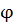 (u)), где y=f(u), u=
(u)), где y=f(u), u= 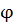 (x), x
(x), x 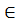 X, причем u=
X, причем u= 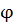 (x) и u=f(u) дифференцируемы соответственно в точках х и u=
(x) и u=f(u) дифференцируемы соответственно в точках х и u= 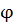 (x). Тогдаdy=F’(x)dx, но F’(x)=
(x). Тогдаdy=F’(x)dx, но F’(x)= 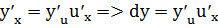 , а т.к.
, а т.к. 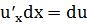 , то dy=
, то dy= 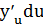
Таким образом форма записи дифференциала сохраняется, если независимую переменную заменить некоторой функцией. Это свойство называется инвариантностью (неизменностью) формы записи дифференциала.
Из инвариантности следует, что, хотя dy= 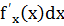 (x- независимая переменная), а dy=
(x- независимая переменная), а dy= 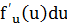 (u=u(x) –функция), запись их одинакова, но сущность этих формул различна. Dx задается произвольно, du задать произвольно нельзя; du нужно вычислять по формуле дифференциала du=u’dx. Это относится и к случаю с несколькими промежуточными функциями.
(u=u(x) –функция), запись их одинакова, но сущность этих формул различна. Dx задается произвольно, du задать произвольно нельзя; du нужно вычислять по формуле дифференциала du=u’dx. Это относится и к случаю с несколькими промежуточными функциями.
n-2. Приближенные вычисления с помощью дифференциала.
По определению dy 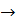 0 при
0 при 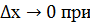 условии, что
условии, что 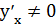 . главная часть приращения функции
. главная часть приращения функции 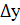 , т.е.
, т.е. 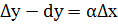 или f(x0+
или f(x0+ 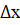 ) - f(x0) - y’(x0)dx =
) - f(x0) - y’(x0)dx = 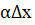 =>f(x0+
=>f(x0+ 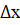 )
) 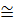 f(x0) +f’(x0)dx
f(x0) +f’(x0)dx
Относительная погрешность при этом при 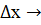 0 становится сколь угодно малой.
0 становится сколь угодно малой.
Если 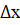 =х-х0, х=х0+
=х-х0, х=х0+ 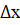 , f(x)
, f(x) 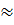 f(x0)+f’(x0)(x-x0) –уравнение касательной к кривой y=f(x) в точке х0, т.е. мы приблизительно заменяем участок кривой y=f(x) отрезком касательной.
f(x0)+f’(x0)(x-x0) –уравнение касательной к кривой y=f(x) в точке х0, т.е. мы приблизительно заменяем участок кривой y=f(x) отрезком касательной.
Если х0=0, то f(x) 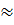 f(0)+f’(0)x. Для 1некоторых элементарных функций имеем:
f(0)+f’(0)x. Для 1некоторых элементарных функций имеем: 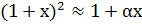 ,
, 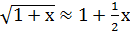 ,
, 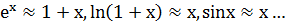
Основной принцип применения дифференциала к приближенным вычислениям значений функций следующий: пусть необходимо для х 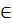 Х вычислить значение функции y=f(x), но этого сделать сразу нельзя, тогда вблизи х ищем значение х0, такое, чтобы f(x0) и f’(x0) легко находилось.
Х вычислить значение функции y=f(x), но этого сделать сразу нельзя, тогда вблизи х ищем значение х0, такое, чтобы f(x0) и f’(x0) легко находилось.
Дата добавления: 2018-08-06; просмотров: 372; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
