Определитель n-го порядка. Теорема о разложении определителя.

Матрицы и линейные операции над ними. Умножение матриц.

Матрицей называется прямоугольная таблица чисел, числа из которых состоит матрица называют её элементами.

Количество строк и столбцов определяют размерность матрицы. Например(m´n). Если количество строк совпадает с количеством столбцов, то матрица – квадратная, в этом случае кол-во строк (столбцов) определяют порядок матрицы.

Матрица у которой диагональные элементы равны единице, а все остальные нулю - называют единичной матрицей.(E,J)

Матрицу С (m´n) называют суммой матриц А и B, если С_ij определяются следующим образом С_ij=a_ij+b_ij

Матрицу С (m´n) называют разностью матриц А и B, если С_ij определяются следующим образом С_ij=a_ij-b_ij

Матрицу С (m´n) называют произведением матрицы А на вещественное число l если С_ij определяются следующим образом С_ij=la_ij

Матрицу С (m´n) называют произведением матрицы А на матрицу В если:

1) Матрица С имеет размерность (m´n)

2) Элементы матрицы С определяются следующим образом:

С_ij= 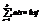, C_ij=a_i₁´b₁_j+a_i₂´b₂_j+a_i₃´b₃_j+…+a_ik´b_kj

Из определения произведения матриц следует, что кол-во столбцов матрицы А должно совпадать с кол-вом строк матрицы В. Произведение матриц вычисляется по правилу “строка на столбец”. Для того чтобы вычислить элемент С_ij необходимо все элементы i строки матрицы А умножить на соответствующие элементы j столбца матрицы В и сложить. А´В¹В´А.

А^*=(а^*_ij) называется транспонированной по отношению к матрице А если выполняется равенство а^*_ij=а_ji, А=(а_ij) таким образом если матрица А имеет размерность (m´n) то А^* имеет размерность (n ´m).

2.Определители квадратных матриц и их свойства. Миноры и алгебраические дополнения.

Определитель состоит из слагаемых, каждый из которых содержит сомножители стоящие в разных строках и столбцах.

Определителем второго порядка называется число (det(A)), которое равно а₁₁´а₂₂-а₁₂´а₂₁, таким образом определителем второго порядка называют следующее выражение

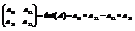
Определителем третьего порядка называется число (det(A)), которое вычисляется при помощи равенства det(A)=a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₃₁a₂₁a₃₂-a₁₃a₂₂a₃₁-a₁₂a₂₁a₃₃-a₁₁a₂₃a₃₂

Свойства определителей

а) Определитель транспонированной матрицы равен определителю исходной матрицы.

б) Если все элементы строки умножить на некоторое число, то и величина определителя умножится на это же число.

в) Если определитель содержит строку (столбец) все элементы которой равны нулю, то такой определитель равен нулю.

г) Если определитель содержит две одинаковые строки (столбца), то этот определитель равен нулю.

д) Если в определителе поменять местами строки (столбцы), то знак определителя изменится на противоположный.

е) Величина определителя не изменится если ко всем элементам одной строки прибавить все элементы другой, умноженные на некоторое число. (Аналогично для столбцов).

ё) Если какую-либо строку определителя можно представить в виде суммы двух строк a₁и a₂, то тогда определитель можно представить в виде суммы двух определителей в одном из которых рассматриваемая строка заменена на строку a₁, а в другом на a₂.

ж) (Теорема Лопласа) Определитель произведения двух матриц равен произведению определителей этих матриц. det(A´B)=det(A)´det(B).

Алгебраические дополнения и миноры.

Минором k-го порядка называют определитель размерностью (k´k), выбранный из матрицы размерностью (m´n).

Если в матрице А вычёркивается строка N_i, а столбец N_j, то минор, получающийся при удалении строки и столбца называется алгебраическим дополнением.

Определитель n-го порядка. Теорема о разложении определителя.

Определителем n-го порядка называется алгебраическая сумма n! слагаемых, каждое из которых представляет произведение n элементов матрицы стоящих в разных строках и разных столбцах, знак с которым каждое слагаемое входит в алгебраическую сумму определяется чётностью подстановки составленной из индексов элементов входящих в данное произведение.

Теорема.

Пусть дана матрица А порядка n, тогда определитель матрицы А можно представить в виде суммы произведений элементов какой-либо строки на их алгебраическое дополнение. Сумма произведений элементов какой-либо строки на соответствующее алгебраическое дополнение элементов другой строки равна нулю. Аналогичное утверждение имеет место для столбцов.

det(A)= 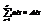, , 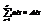если i¹j. 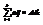, если j¹k.

Данная теорема позволяет сводить вычисления порядка n к порядку n-1. Если определитель матрицы А равен нулю, то такая матрица называется вырожденной. Если какой-нибудь минор равен нулю, то он называется вырожденным минором.

Наивысший порядок не вырожденных миноров называют – рангом (rang(A))

4. Обратная матрица. Построение обратной матрицы.

Пусть дана квадратная матрица А=(a_ij), матрица В называется обратной по отношению к матрице А, если выполняется равенство: А´В=В´А=Е. Если такая матрица В существует, то её обозначают А^-1.

Метод Гаусса нахождения обратной матрицы:

1) Строится матрица Ã=(А/Е), которая получается из матрицы А приписыванием справа единичной матрицы.

2) При помощи элементарных преобразований матрицу Ã приводят к виду (Е/В), если это удаётся сделать, то матрица В будет обратной. Если невозможно, то обратной матрицы не существует, как правило это происходит тогда, когда в результате элементарных преобразований получается матрица, у которой в некоторой строке первые n элементов равны нулю.

5. Системы линейных уравнений. Основные понятия и определения.

Системой линейных уравнений называют систему равенств:

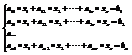
a_ij, b_j_–заданные. x_j_–неизвестная.

Решением этой системы называется такой набор чисел x₁, x₂,…x_n. для которых уравнения превращаются в верные равенства.

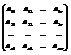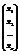A= , Х= , В=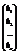

Х и В – называются вектор столбцами. В матричном виде система выглядит А´Х=В.

Система называется совместной, если она имеет хотя бы одно решение, в противном случае система не совместна.

Система называется определённой, если она имеет единственное решение, если система имеет более одного решения то система неопределённая.

Решение системы линейных уравнений с помощью метода Крамера.

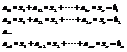
Где А_ij – алгебраические дополнения. Умножим первое у-е на А₁₁, а второе на А₂₁ и тд. Сложим получившиеся равенства:

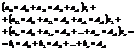
По теореме о разложении определителя по элементам столбца сумма слагаемых стоящих перед x₁ будет равна определителю матрицы А. Сумма слагаемых перед x₂ и x₁ будет равна нулю. В правой части равенства стоит величина равная определителю, который получается из определителя матрицы А с заменой первого столбца на вектор столбец В. Обозначим этот определитель через 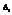, тогда равенство можно записать в виде 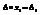, если первую строку системы умножить на А₂₁ и тд., и сложим получившиеся равенства, то получим 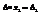, где 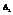- определитель полученный из определителя матрицы А заменой второго столбца на вектор столбец В. Продолжая этот процесс получим систему линейных уравнений:

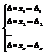
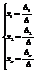
Числа x_1, x₂, …x_n являются решениями системы.

6. Решение системы линейных уравнений с помощью обратной матрицы. Метод Гаусса решения систем линейных уравнений.

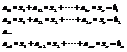
Для данной системы построим расширенную матрицу, Ã которая равна:

Ã=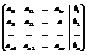

Будем выполнять над матрицей А элементарные преобразования так, чтобы привести её к виду, когда все элементы лежащие ниже диагонали будут равны нулю. Под элементарными преобразованиями понимают: изменение местами двух строк (столбцов) матрицы Ã; прибавление к элементам одной строки элементов другой умноженных на некоторое число.

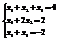Ã =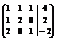

Расширенная матрица иногда называется присоединённой. Каждой системе линейных уравнений соответствует своя матрица Ã, зная матрицу Ã можно записать систему линейных уравнений, которая ей соответствует.

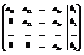
Если k¹n, то такой вид матрицы называется трапецевидный.

Если k=n, то такой вид матрицы называется треугольный.

Если получается трапецевидная матрица в процессе элементарных преобразований, это означает что система имеет не одно решение.

Если получается треугольный вид то матрица имеет одно решение.

Если матрица Ã приведена к трапецевидному виду, то перенося все неизвестные, которые расположены правее диагонали и придавая им произвольные значения, можно найти всевозможные решения первоначальной системы.

7. Однородные системы. Условия существования нулевых решений. Понятие ранга матрицы.

Рассмотрим А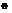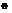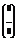Х= , = , Х= - векторстолбец.

Эта однородная система всегда является совместной, т.к. она всегда имеет решение х=0. Решения этой системы обладают свойствами:

Если х₁ и х₂ являются решениями системы, то 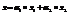так же является решением этой системы.

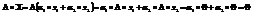
Говорят, что решение однородной системы образует конечномерное линейное векторное пространство.

Пусть имеется 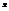векторов: .

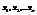Векторы 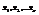называют линейно независимыми, если из равенства 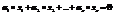следует, что все 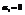, в противном случае если векторы 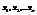линейнозависимые.

Пусть матрица А имеет вид:

, , ,

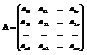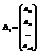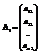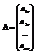
Тогда систему можно записать в виде 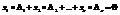, из равенства видно что если система не имеет не нулевых решений, то векторы 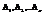являются линейнонезависимыми. Если система имеет нулевое решение, то векторы 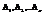являются линейнозависимыми.

Теорема:

Для того чтобы векторы 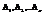были линейнонезависимы, необходимо и достаточно чтобы ранг матрицы А образованный этими элементами равнялся n. Таким образом, чтобы решить однородную систему у-ий АХ= 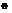необходимо выполнить следующие действия: вычислить ранг матрицы А, если ранг совпадает с числом неизвестных, то однородная система линейных у-ий имеет одно решение. Если ранг матрицы А меньше числа неизвестных, то в матрице А можно найти S строк и S столбцов, таких, что определитель составленный из элементов лежащих на пересечении выбранных строк и столбцов не равнялся нулю.

Предположим для определённости, что определитель состоит из S строк и S столбцов отличных от нуля, тогда перенося слагаемые 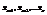в правую часть и оставляя в системе первые S уравнений, получим систему:

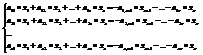(3)

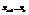- свободные неизвестные (базисные неизвестные), придавая базисным неизвестным произвольные числовые значения из системы (3) можно найти 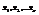, таким образом однородная система линейных у-ий может иметь одно или бесконечное множество решений, отсюда следует, что 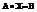может иметь бесконечное кол-во решений или быть несовместной.

Минором k-го порядка называют определитель размерностью (k´k), выбранный из матрицы размерностью (m´n).

Наивысший порядок не вырожденных миноров называют – рангом (rang(A))

9. Векторные величины. Линейные операции с векторами.

Вектор – направленный отрезок, таким образом, чтобы задать вектор необходимо задать его длину и направление.

Два вектора называют равными, если они имеют одинаковую длину и направление.

Вектор называют нулевым, если длина равна нулю (он не имеет направления).

Если на плоскости введена прямоугольная система координат, то для того чтобы задать вектор надо указать начало вектора т. А и его окончание т. В., в этом случае вектор обозначается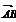

Пусть т. А имеет координаты 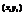, т. В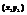

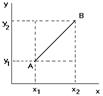
Тогда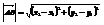

Пусть a и b обозначают углы, которые образует вектор 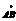с положительным направлением координатных осей. a и b - углы определяющие направление вектора 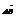, cos этих углов называются направляющими:

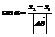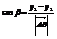
т.к. при параллельном переносе ни длина ни направление вектора не изменяется, то удобно расположить все векторы таким образом, чтобы они начинались в начале координат. В этом случае для задания вектора достаточно указать т., где он заканчивается.

Действия с векторами.

На основе полученных векторов, построим параллелограмм. Проведём диогональ АВ. Тогда 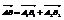Для каждого вектора АВ не равного нулевому существует противоположный, который такой же длины но другого направления. Вектор обратный вектору АВ, обозначается (-АВ)

Разностью двух векторов А₁В₁ и А₂В₂ называют вектор .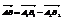

Вектор АВ называется произведением вектора А₁В₁ на вещественное число l и обозначается следующим образом:

а) если длина вектора АВ равна l 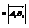и вектор АВ имеет тоже направление что и вектор А₁В₁.

б) если l=0, то l 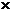А₁В₁=0

в) если l<0, то l 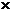А₁В₁=(-( ))

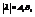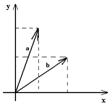
10. Скалярным произведением векторов a и b называют число равное произведению длин этих векторов на cos угла между ними. Пусть ça çи çb ça - угол между векторами, тогда из определения следует ab = ça ç× çb çcos a. Пусть a1 – угол который образует вектор a с положительным направлением оси ОХ. a2 – угол который образует вектор b с положительным направлением оси ОХ. a=a1-a2 ab = êaê×êbêcos (a1-a2).

êa êcos a1 × êb êcos a2 + êa êsin a1 × êb êsin a2 = x1x2+y1y2. Таким образам скалярное произведение векторов a и b можно вычислить как сумму произведения их соответствующих координат. Это определение скалярного произведения эквивалентно первоначальному. Свойства векторов: 1.)ab = ba. 2.)a × 0 = 0. 3.) a(b +c) = ab + ac. 4.) (la) × (lb) = l(ab). 5.) aa = êa ê². 6.) aa ³ 0 aa = 0 Û a = 0. 7.) ab = 0 Û a ^ b. Предполагается, что нулевой вектор ^ любому вектору. Аналогичным образом определяется скалярное произведение для векторов расположенных в трехмерном пространстве свойства 1 –7 остаются неизменными.

11. Линейная зависимость и независимость векторов. Коллинеарные и компланарные вектора.

Два вектора называются коллинеарными, если они лежат на одной прямой или на || прямых.

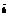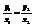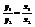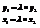Если векторы и являются коллинеарными, то они наклонены под одним и тем же углом положительного направления оси ОХ, значит Þ , Þ 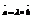- условие коллинеарности векторов.

Два вектора называются компланарными если они находятся в разных плоскостях и не пересекаются.

12. Декартовая прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком – нибудь порядке. Точка пересечения осей называется началом координат, а сами оси – координатными осями. Первая из координатных осей называется осью абсцисс, а вторая – осью ординат. Начало координат обозначают буквой О, ось абсцисс – символом ОХ, ось ординат – символом ОУ. Координатами произвольной точки М в заданной системе называют числа Х = ОМх, У = ОМу, где Мхи Му суть проекции точки М на оси ОХ и ОУ, ОМх обозначает величину отрезка ОМх оси абсцисс, ОМу – величину отрезка ОМу оси ординат. Число Х называется абсциссой точки М, число У называется ординатой этой же точки. Символ М (Х; У) обозначает, что точка М имеет абсциссой число Х, а ординатой число У. Ось ОУ разделяет всю плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси ОХ, называется правой, другая – левой. Точно так же ось ОХ разделяет плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси ОУ, называется верхней, другая нижней.

Обе координатные оси вместе разделяют плоскость на четыре четверти, которые номеруют по следующему правилу: первой координатной четвертью называется та, которая лежит одновременно в правой и в верхней полуплоскости, второй – лежащая в левой и в верхней полуплоскости, третьей – лежащая в левой ив нижней полуплоскости, четвертой – лежащая в правой и в нижней полуплоскости.

13. Векторным произведением вектора a на векторbназывается вектор, обозначаемый символом [ ab ] и определяемый следующими тремя условиями: 1) модуль вектора [ ab ] равен ïaï× ïbï sin j, гдеj - угол между векторамиa иb; 2) вектор [ ab ] не

неперпендикулярен к каждому из векторовa и b; 3) направление вектора [ab] соответствует «правилу правой руки». Это означает, что если вектор a, b и [ab] приведены к общему началу, то вектор [ab] должен быть направлен так, как направлен средний палец правой руки, большой палец которой направлен по первому сомножителю (т. е. по векторуa), а указательный – по второму (т. е. по векторуb). Векторное произведение зависит от порядка сомножителей, именно: [ab] = -[ab]. Модуль векторного произведения [ab] равенSпараллелограмма, построенного на векторахa и b: ê[ab] ê = S. Само векторное произведение может быть выражено формулой [ab] = Se, где e – орт векторного произведения. Векторное произведение [ab] обращается в нуль тогда и только тогда, когда векторы a и b коллинеарны. В частности [aa ] = 0. Если система координатных осей правая и векторы a и bзаданы в этой системе своими координатами: a = {X1; Y1; Z1}, b = {X2;Y2;Z2}, то векторное произведение вектора a на вектор b определяется формулой[ab] = 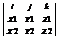Свойства:1) aa =q 2) ab = (ba) 3) a(b1 + b2) = ab1 + ab2 4) (la)b = a(lb) = l(ab).

Смешанное произведение.Пусть даны a(X1; Y1; Z1), b(X2; Y2; Z2), c(X3; Y3; Z3).

Смешанным произведением трех векторов a, b, c называется число, равное векторному произведению [ab],умноженному скалярно на вектор c, т. е. [ab]c. Именно место тождество: [ab]c = a[bc], ввиду чего для обозначения смешанного произведения [ab]c употребляется более простой символ: abc.Таким образом, a,b,c = [ab]c, abc = a [bc].Смешанное произведение abcравно объему параллелепипеда, построенного на векторах a, b, c,взятому со знаком плюс. Если векторы a,b,cкомпланарны (и только в этом случае), смешанное произведение abcрано нулю; иначе говоря, равенство abc = 0, есть необходимое и достаточное условие ком планарности векторов a,b,c.Если векторы a,b,cзаданы своими координатами: a ={X1; Y1; Z1}, b = {X2; Y2; Z2}, c = {X3;Y3;Z3;}

14. Простейшие задачи аналитической геометрии.1) Вычислим расстояние между двумя точками на плоскости: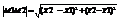

2) Деление отрезков в данном отношении. Пусть на плоскости даны две точки с координатами М1(X1;Y1) и M2(X2;Y2). Найти координаты точки М лежащей между М1 и М2 на отрезке М1М2, если выполняется условие: 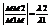. Проекции точки М на ось абсцисс будет делить отрезок X1X2 в той же самой проекции, потому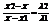 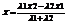, l1X2 - l1X = l2X - l2X1. Аналогичным образом можно получить, что , , ,

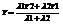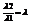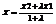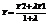
Полярные координаты.

Полярная система координат определяется заданием некоторой точки О, называемой полюсом, луча ОА, исходящего из этой точки, называемого полярной осью, и масштаба для измерения длин. Кроме того, при задании полярной системы должно быть сказано, какие повороты вокруг точки О считаются положительными. Полярными координатами произвольной точки М (относительно заданной системы) называются числа r = ОМ и q < АОМ. Угол q при этом следует понимать так, как принято в тригонометрии. Число r называется первой координатой, или полярным радиусом, число q- второй координатой, или полярным углом точки М. Символ М (r;q) обозначает, что точка М имеет полярные координаты r и q. Полярный угол q имеет бесконечно много возможных значений. Значение полярного угла, удовлетворяющее неравенствам -p < q ≤ +p, называется главным. В случаях одновременного рассмотрения декартовой и полярной систем координат условимся: 1) пользоваться одним и тем же масштабом, 2)при определении полярных углов считать положительными повороты в том направлении, в каком следует вращать положительную полуось абсцисс, чтобы кратчайшим путем совместить ее с положительной полуосью ординат. При этом условии, если полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс, то переход от полярных координат произвольной точки к декартовым координатам той же точки осуществляется по формулам 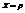cosq, 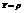sinq. В этом же случае формулы 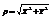, tgq = 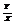являются формулами перехода от декартовых координат к полярным. При одновременном рассмотрении в дальнейшем двух полярных систем координат условимся считать направление положительных поворотов и масштабов для обеих систем одинаковыми.

Дата добавления: 2018-08-06; просмотров: 536; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!