Свойства биноминальных коэффициентов
Решение задач на перебор вариантов
Цель работы:
студент должен:
знать:
- определение соединений, их видов;
- определение вероятности;
- теоремы сложения, умножения вероятностей;
уметь:
- по условию задачи различать виды соединений;
- вычислять разные виды соединений;
- вычислять вероятность событий.
Сведения из теории:
Соединения, их виды
Группы, составленные из каких – либо элементов, называются соединениями.
Различаю три основных вида соединений: размещения, перестановки и сочетания.
Размещениями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
Число размещений из n элементов по m обозначается и вычисляется по формуле:
.
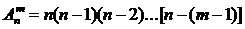Перестановками из n элементов называются такие соединения из всех n элементов, которые отличаются друг от друга порядком расположения элементов.
Перестановки представляют частный случай размещений из n элементов по n в каждом.
Число всех перестановок из n элементов равно произведению последовательных чисел от 1 до n включительно:
,
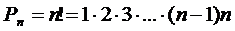n!-читается «n-факториал», причем 0!=1 и 1!=1.
Используя приведенные выше определения имеем формулы:
,
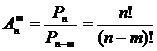при решении задач часто используется равенство:
.
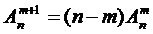Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.
|
|
|
Число сочетаний из n элементов по m обозначается и вычисляется по формуле:
,
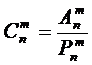которую можно записать также в виде
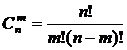
или
.
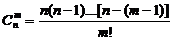Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:
, 
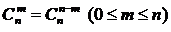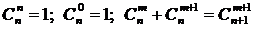
Пример 94.
Найти число размещений из 10 элементов по 4.
Решение:
по формуле :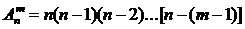
.
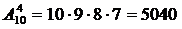Пример 95.
Решить уравнение: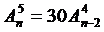 
.
Решение:
используя формулу для вычисления числа размещений имеем:
.
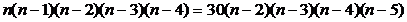Разделим обе части на одинаковые выражения, получим:
,
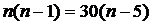и решим получившееся квадратное уравнение: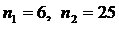 
.
Пример 96.
Решите систему: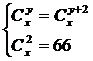 
.
Решение:
решим второе уравнение:
.
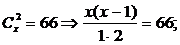
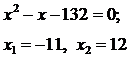Т. к.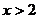 
, то –11 не удовлетворяет условию задачи. Подставив х=12 в первое уравнение системы, получим
.
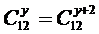Используя основное свойство сочетаний, имеем:
,
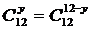тогда
.
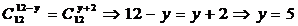Ответ: х=12, у=5.
Пример 97.
Сколькими способами из восьми кандидатов можно выбрать три лица на три должности?
Решение:
условию задачи соответствуют размещения 3 из 8, имеем:
.
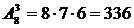Случайные события
Изучение каждого явления в порядке наблюдения или производства опыта связано с осуществлением некоторого комплекса условий (испытаний). Всякий результат или исход испытания называется событием.
|
|
|
Если событие при заданных условиях может произойти или не произойти, то оно называется случайным.
В том случае, когда событие должно непременно произойти, его называют достоверным, а в том случае, когда оно заведомо не может произойти, невозможным.
События называются несовместными, если каждый раз возможно появление только одного из них. События называются совместными, если в данных условиях появление одного из этих событий не исключает появление другого при том же испытании.
События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны.
Вероятность события рассматривается как мера объективной возможности появления случайного события.
Классическое определение вероятности.
Вероятностью событияА называется отношение числа благоприятных исходов m, к числу всех возможных исходов n:
.
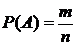Вероятность любого события не может быть меньше нуля и больше единицы, т. е.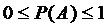 
.
Невозможному событию соответствует вероятность Р(А)=0, а достоверному – вероятность Р(А)=1.
Пример 98.
В лотерее из 1000 билетов 200 выигрышных. Вынимают наугад один билет. Какова вероятность, что этот билет выигрышный?
|
|
|
Решение:
количество благоприятных событий, удовлетворяющих условию задачи m=200.
Число всех возможных вариантов n=1000.
По определению вероятности: Р(А)=200/1000=0,2.
Пример 99.
Из урны, в которой находятся 5 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что этот шар черный?
Решение:
общее число шаров m=8, из них черных n=3, по определению: Р(А)=3/8=0,375.
Пример 100.
Из урны, в которой находятся 12 белых и 8 черных шара, вынимают наудачу два шара. Найти вероятность того, что оба шара окажутся черными?
Решение:
общее число возможных случаев n равно числу сочетаний из 20 (12+8) элементов по два:
;
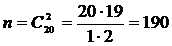число благоприятных исходов m равно числу сочетаний из 8 элементов по два:
.
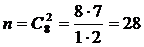По определению: Р(А)=28/190=0,147.
Пример 101.
В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Какова вероятность того, что из этих 5 деталей две окажутся бракованными?
Решение:
число всех равновозможных независимых исходов n равно числу сочетаний из 18 по 5:
.
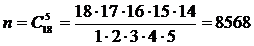Подсчитаем число благоприятных исходов m. Среди 5 взятых наугад деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2:
|
|
|
.
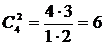Число способов выборки трех качественных деталей из 14 имеющихся равно числу сочетаний из 14 по 3:
.
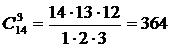Любая группа качественных деталей может комбинироваться с любой группой бракованных, поэтому общее число комбинаций m равно:
,
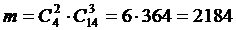по определению: Р(А)=2184/8568=0,255.
Задания для самостоятельного решения:
Решить следующие задачи, используя определение сочетаний, их видов:
1 вариант
1) Сколько двузначных чисел можно составить из цифр 1, 3, 5, 8, 9 так, чтобы в каждом числе не было одинаковых цифр?
2) Из 6 открыток надо выбрать 3. Сколькими способами это можно сделать?
3) Решите уравнение:  .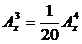
| 2 вариант
1) Сколькими способами могут разместиться 5 человек вокруг круглого стола?
2) Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал семи различных цветов?
3) Решите уравнение:  .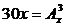
|
3 вариант
1) Из 10 кандидатов нужно выбрать 3 человека на конференцию. Сколькими различными способами это можно сделать?
2) Сколько различных пятизначных чисел можно составить из цифр 0, 1, 3, 5, 7 так, чтобы в каждом числе не было одинаковых цифр?
3) Решите уравнение:  .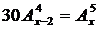
| 4 вариант
1) Бригадир должен отправить на работу бригаду из 3 человек. Сколько таких бригад можно составить из 8 человек?
2) На собрании должны выступить 5 человек (А, Б, В, Г, Д). Сколькими способами их можно разместить в списке выступающих, еслиА должен выступать первым?
3) Решите уравнение:  .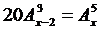
|
5 вариант
1) Сколькими способами можно расставить на полке 6 книг?
2) Сколькими способами можно выбрать гласную и согласную буквы из слова «журнал»?
3) Решите уравнение:  .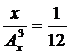
| 6 вариант
1) Сколькими способами можно составить список из 6 человек?
2) Сколькими способами собрание, состоящее из 18 человек, может из своего состава выбрать председателя собрания и секретаря?
3) Решите уравнение:  .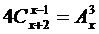
|
7 вариант
1) Среди перестановок из цифр 1, 2, 3, 4, 5 сколько таких, которые не начинаются цифрами 3 или 5?
2) Из города А в город В ведут 6 дорог, а из города В в город С –3 дороги. Сколькими способами можно попасть из города А в город С?
3) Решите систему:  .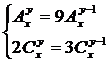
| 8 вариант
1) В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий сыграно в этом турнире?
2) Имеется 8 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну перчатку на правую руку так, чтобы эти перчатки были разных размеров?
3) Решите систему:  .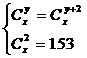
|
| 9 вариант 1) Группа учащихся изучает семь учебных дисциплин.сколькими способами можно составить расписание занятий на понедельник, если в этот учебный день должно быть четыре различных урока? 2) Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой один раз? 3) Вычислить: | |
.Контрольные вопросы:
1. Дайте определение соединения, их виды?
2. Приведите формулы для вычисления разных видов соединений.
3. Дайте определение случайного события, их виды. Приведите примеры.
4. Дайте классическое определение вероятности.
Литература:[5, с. 234-238]
Практическая работа № 41
Свойства биноминальных коэффициентов
Цель работы:
студент должен:
знать:
- формулу бинома Ньютона;
- свойства биноминальных коэффициентов;
уметь:
- раскладывать бином по степеням х;
- возводить в различные степени трехчлены.
Сведения из теории:
Формула бинома Ньютона
Бином Ньютона – это формула разложения степени двучлена (бинома) (a+b)n в виде многочлена от a и b.
Запишем разложения бинома Ньютона для нескольких первых значений n:
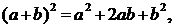
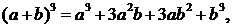
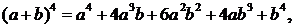
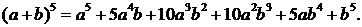
Чтобы найти коэффициент при akbn-kв разложении бинома (a+b)n в общем случае, представим себе, что мы перемножаем n скобок и приводим подобные члены. Член akbn-kвстретится столько раз, сколько можно указать k скобок (из n возможных), из которых мы возьмем множитель а (а из остальных автоматически возьмем b). Это число равно числу выборок k скобок из n возможных, которое носит название числа сочетаний из n по k и обозначается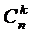 
.
В этих обозначениях формула имеет следующий вид:
.
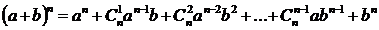Иными словами, число сочетаний из n по k равно коэффициенту при члене an-kbkв разложении n-ой степени двучлена (a+b) поэтому числа сочетаний называют иначе биномиальными коэффициентами.
Эту связь можно использовать для вывода свойств сочетаний алгебраическими методами. Такой подход к выводу свойств комбинаторных объектов носит название метода производящих функций.
Свойства биномиальных коэффициентов
Биномиальные коэффициенты обладают большим количеством свойств.
Свойство 1.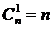 
.
Свойство2.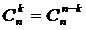 
– биномиальные коэффициенты, равноотстоящие от концов, равны между собой
Свойство3.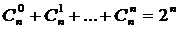 
– сумма биномиальных коэффициентов при фиксированномn равна 
.
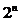Свойство4.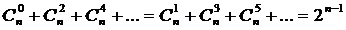 
– суммы биномиальных коэффициентов, стоящих на четных и на нечетных местах, равны между собой (и равны по половине от общей суммы).
Свойство5.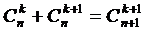 
– рекуррентное соотношение, связывающее биномиальные коэффициенты для соседних степеней.
Пример 102.
Разложить бином (1+х)6 по степеням x.
Решение:
применяем формулу бинома Ньютона:
.
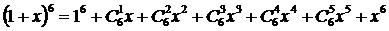Значения биномиальных коэффициентов находим последовательно по формуле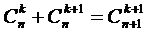 
:
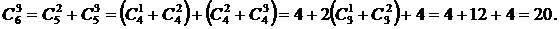
Т.о.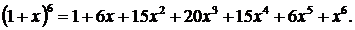 
Задача для самостоятельного решения №1.Разложить бином (1+х)5 по степеням x.
Пример 103.
Возвести трехчлен a+b+c в четвертую степень.
Решение:
применяем формулу бинома Ньютона:
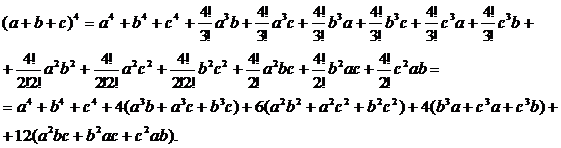
Задача для самостоятельного решения №2.Возвести трехчлен a+b+c в третью степень.
Контрольные вопросы:
1. Запишите формулу бинома Ньютона.
2. Перечислите свойства биноминальных коэффициентов.
Литература: [16]
Практическая работа № 42
Треугольник Паскаля
Цель работы:
студент должен:
знать:
- принцип построения треугольника Паскаля;
уметь:
- возводить двучлен в любую натуральную степень.
Сведения из теории:
Треугольник Паскаля – бесконечная таблицабиномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоятединицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван треугольник в честьБлеза Паскаля.
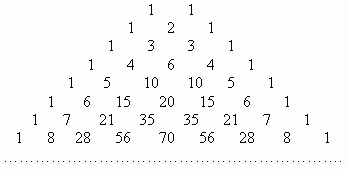
Первая строка в этой таблице содержит биномиальные коэффициенты для n=1; вторая – дляn=2; третья – дляn=3 и т.д.
Пример 104.
Разложить выражение:(a+b)7.
Решение:
мы можем получить результат моментально, используя из таблицы разложение по седьмой строке (т.к. седьмая степень двучлена):
.
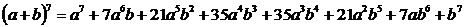Задача для самостоятельного решения №1.Построить треугольник Паскаля до двадцатой строки.
Задача для самостоятельного решения №2.Разложить выражение:(a+b)n, гдеn–номер по журналу (если Ваш номер 1-7, то прибавьте к номеру число 5).
Контрольные вопросы:
1. Сформулируйте принцип построения треугольника Паскаля.
Дата добавления: 2018-08-06; просмотров: 1089; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!
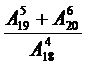