Силы противодействующие вытеснению нефти из пласта

Силы, противодействующие вытеснению нефти из пласта.

1) силы вязкого трения,

2) капиллярные силы

3) адгезионные силы (силы прилипания).

Силы трения проявляются в пласте также как и при течении нефти и газа по трубопроводу, т.е. гидравлическое сопротивление течению нефти в порах пропорционально скорости фильтрации и вязкости.

В пласте действует капиллярные силы. Эти силы проявляются в зоне контакта несмешивающихся жидкостей. При вытеснении нефти водой за фронтом вытеснения образуется, формируется многочисленные столбики нефти, рассеянные в воде и в этой зоне особенно сильно проявляются капельные силы.

Молекулярные силы взаимодействия между различными веществами, насыщающими горные породы, играют важную роль в процессах извлечения нефти и газа из недр. Капиллярные силы представляют собой одну из форм проявления межмолекулярных сил.

Р1 > Р2 Р1-Р2 = ΔР

Чтобы рассмотреть кап. Силы, рассмотрим капилляр со столбиком нефти, который вытесняется водой при Р1-Р2 = ΔР.

В статич. Условиях под действием кап. сил столбик нефти стремится принять шарообразную форму, оказывая давление Р на стенки пор через пленку воды. При этом давление Р, возникающее внутри капилляра:

P=(2σ / R) – σ/r , где

Р – давление; σ – коэффициент поверхностного натяжения на границе раздела фаз; R – радиус сферической поверхности столбика воды; r – радиус цилиндрической поверхности

Установлено что R и r и cosθ связаны между собой следующей зависимостью:

R=r/cosΘ

Получим: P=2σcosΘ/r - σ/r = (2σ/r)*(cosΘ-0.5)

При Θ=0 давление P=σ/r

Из формулы видно, что чем больше σ и меньше r, тем больше Р оказываемое на стенки пор через пленку воды и тем вероятнее неподвижность столбика нефти в капилляре.

Если на концах капилляра создать перепад Р то произойдет деформация нефти ( см. пунктирную линию).

Такое изменение формы менисков вызовет соответствующее им изменение кап давления, которое согласно закону Лапласа будут слудующими:

Для левого мениска : P¹=σ/R¹

Для правого мениска : P¹¹=σ/R¹¹

Р¹>Р¹¹.

Разность этих кап давлений будет создавать силу, противодействующую внешнему перепаду давлений ΔР.

P_КАП=(2σ/ R¹¹) - (2σ/ R¹)

P_КАП=(2σ/r)*(cosΘ₂-cosΘ₁)

Это явление когда возникает дополнительное сопротивление при движении двух не смещающихся жидкостей или пузырьков газа называют эффектом Жамена.

Т.к. таких столбиков или пузырьков газа в поровых каналах очень много, то на преодоление кап сил затрачивается существенная доля ΔР. Те же самые явления наблюдаются при переходе капли из широкой части капилляра в узкую, возникает также разность кап давлений менисков, имеющих разные радиусы.

Адгезия – слипание поверхностей двух соприкасающихся разнородных твердых или жидких тел (в физике).

Когезия (от лат. cohaesus - связанный, сцепленный) — сцепление друг с другом частей одного и того же тела (жидкого или твердого). Обусловлена химической связью и межмолекулярным взаимодействием.

Работа адгезии оценивается уравнением Дюпре:

Wa = σ_1,2 + σ_2,3– σ_1,3, где

где σ₁₂ — поверхностное натяжение жидкости на границе с воздухом; σ₃₂ и σ₃₁ — поверхностное натяжение твердого тела на границе с воздухом и с жидкой фазой.

Уравнение Дюпре — Юнга:

W=σ_1,2*(1+cosΘ)

Из уравнения следует, что на отрыв жидкости от поверхности твердого тела при полном смачивании, когда cosΘ=1 , затрачивается работа W=2σ₁₂ , необходимая для образования двух жидких поверхностей.

Это значит, что при полном смачивании жидкость отрывается не от поверхности твердого тела, а происходит разрыв самой жидкости, т. е. при полном смачивании σ₁₂<σ₃₁ .

Для гидрофобных поверхностей характерно соотношение σ₁₂>σ₁₃ , т. е. жидкость может отрываться от поверхности. При Θ = 180°, т. е. при полной несмачиваемости жидкостью поверхности твердого тела, работа адгезии равна нулю. Следовательно, работа адгезии может служить показателем смачиваемости или прилипаемости жидкостей к поверхности твердого тела.

Поверхность горных пород отличается значительной неоднородностью по смачиваемости. Это можно объяснить многими причинами. Большое влияние на свойства поверхностей оказывают процессы адсорбции, которые зависят от большого многообразия факторов, связанных как с составом пластовых жидкостей и пород, так и с условиями их контакта в пласте. Свойства поверхности минералов, кроме явлений адсорбции, зависят и от процессов химического взаимодействия жидкостей и минералов, ионного обмена, растворения и электрокинетических явлений. Значительно влияет на эти процессы сложное строение самой поверхности минералов. Вследствие влияния на свойства поверхности горных пород большого числа факторов, избирательная смачиваемость их пластовыми жидкостями может изменяться в широких пределах. Некоторые породы, по-видимому, полностью гидрофобизованы нефтью. Большинство же исследованных коллекторов газовых месторождений сложены гидрофильными породами.

1 Закон Дарси. Коэффициент фильтрации. Зависимость коэффициента фильтрации от свойств пористой среды и фильтрующейся жидкости
Согласно закону Дарси скорость фильтрации жидкости в пористой среде пропорциональна градиенту давления и обратно пропорциональна динамической вязкости жидкости

v – скорость линейной фильтрации м/с;

Q – объемный расход жидкости в ед. времени, м³/сек;

F – площадь сечения образца, м²;

∆Р – перепад давления; Па

L – длина образца, м;

µ - динамическая вязкость жидкости, Па·с;

k – коэф. проницаемости, м².

Основное соотношение теории фильтрации - закон фильтрации устанавливает связь между вектором скорости фильтрации и тем полем давления, которое вызывает фильтрационное течение. Первые экспериментальные наблюдения за движением воды в трубах, заполненных песком, провели французские инженеры А. Дарси (1856 г.) и Ж. Дюпюи (1848 1863 гг.). Анри Дарси исследовал течение воды через вертикальные песчаные фильтры что требовалось для нужд водоснабжения г. Дижона. В результате тщательно проведенных экспериментов он установил получившую широкую известность экспериментальную формулу

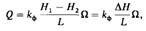
где Q объемный расход жидкости через песчаный фильтр, длина которого L, а площадь поперечного сечения Ω; ΔH= Н₁ — Н₂ - разность напоров воды над фильтром и у его основания; - коэффициент пропорциональности в формуле, названный первоначально коэффициентом водопроницаемости, а затем коэффициентом фильтрации, который зависит как от природы пористой среды, так и от свойств фильтрующейся жидкости. Этот коэффициент имеет размерность скорости и характеризует скорость потока через единицу площади сечения, перпендикулярного к потоку, под действием единичного градиента напора.

Коэффициент фильтрации используется обычно в гидротехнических расчетах, где приходится иметь дело с одной жидкостью-водой. При исследовании фильтрации нефти, газа и их смесей необходимо разделить влияние свойств пористой среды и жидкости. В этом случае формула Дарси записывается обычно в несколько ином виде, а именно:

ИЛИ

где η динамический коэффициент вязкости, Δр* = рgН = р + pgz-приведенное давление¹; К-коэффициент проницаемости, который не зависит от свойств жидкости и является динамической характеристикой только пористой среды. Из (1.6) следует, что коэффициент проницаемости имеет размерность площади, так что в СИ [к] = м². При этом проницаемость большинства горных пород выражается весьма малыми числами.

Связь между коэффициентами фильтрации и проницаемости к:

Коэффициент фильтрации k_ф или коэффициент проницаемости к определяют экспериментально в специальном приборе - пермеаметре, содержащем образец исследуемого грунта. Общий расход Q фильтрационного потока при этом поддерживается постоянным. Напоры H₁ и H₂ измеряются двумя пьезометрами, соединенными с пористой средой в сечениях 1 и 2. Превышения центров сечений над плоскостью сравнения равны z₁ и z₂, а давления р₁ и р₂\ расстояние между этими сечениями по оси цилиндра составляет L.

В соответствии с формулами указанными выше::

Одним из основных законов теории фильтрации является установленный в 1856 г. закон Дарси, дающий связь между потерей напора H₁ — Н₂ и объемным расходом жидкости Q, текущей в трубке с площадью поперечного сечения f, заполненной пористой средой.

Закон Дарси имеет вид: Q=(c*(H₁-H₂)*f)/L , где

c – коэффициент пропорциональности, называемый коэффициентом фильтрации

Закон Дарси показывает, что между потерей напора и расходом существует линейная зависимость. При повышении скорости движения жидкости линейность, т. е. закон Дарси, нарушается. Критерием справедливости закона Дарси обычно служит сопоставление числа Рейнольдса Re =u*a*ρ/μ с его критическим значением Re_Kp, после которого линейная связь между, потерей напора и расходом нарушается. В выражении числа Re: ρ — плотность жидкости; μ— ее абсолютная или динамическая вязкость; u — характерная скорость течения; а — характерный геометрический размер пористой среды, который разные авторы определяют по-разному.

Запишем закон Дарси в дифференциальной форме. В общем случае Н = Н (s, t), где s — расстояние вдоль оси криволинейной трубки тока; t — время.

Закон Дарси в дифференциальной форме:

w=Q/f=-c*dH/ds

w= -c*gradH

Итак, закон Дарси заключается в том, что скорость фильтрации пропорциональна градиенту давления.

Закон Дарси имеет силу, если соблюдаются следующие условия:

1) мелкозернистая пористая среда или достаточно узкие поровые каналы;

2) малая скорость фильтрации или небольшой градиент давления;

3) незначительные изменения скорости фильтрации или градиента давления.

Коэффициент фильтрации с характеризует среду и жидкость одновременно. Этот коэффициент обычно используется в гидротехнических расчетах, где приходится иметь дело с одной жидкостью — водой. В теории фильтрации нефти и газа необходимо разделить влияние пористой среды и влияние жидкости. Поэтому закон Дарси записывается обычно в несколько ином виде, а именно:

w=(-k*γ/μ)*dH/ds

w=(k/μ)*dp/ds

где (μ- — абсолютный коэффициент вязкости; γ — объемный вес жидкости; k — коэффициент проницаемости, характеризующий среду р = γН — приведенное давление. Очевидно, что приведенное давление совпадает с истинным при z = 0.

Коэффициент фильтрации:

c=kγ/μ

Коэффициент фильтрации зависит от свойств пористой среды и свойств фильтрующейся жидкости. Наибольшее влияние на этот коэффициент оказывают размеры частиц породы. Величина зависит также от формы частиц, степени шероховатости их поверхности, пористости среды, вязкости жидкости.

Дата добавления: 2018-08-06; просмотров: 1082; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 7 8 9 10 111213 14 15 16 Следующая ⇒

Мы поможем в написании ваших работ!