Интегралы от непрерывных функций.
Раздел 5. Определённый интеграл.[1,4 доп. лит.]
Задачи, приводящие к понятию определённого интеграла.
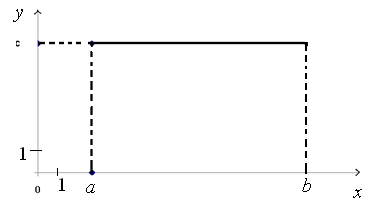
П.1. Площадь криволинейной трапеции.
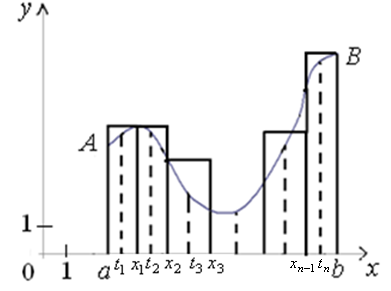
 ,
, 
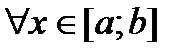 ,
, 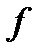 – непрерывна на
– непрерывна на 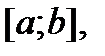

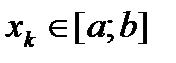 ,
, 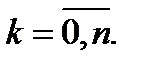
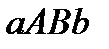 – криволинейная трапеция;
– криволинейная трапеция; 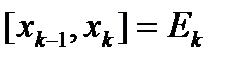 ,
, 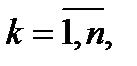
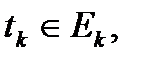
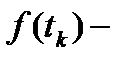 высота прямоугольника,
высота прямоугольника,
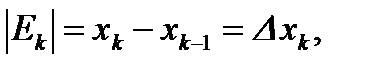
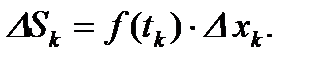
Площадь ступенчатой фигуры 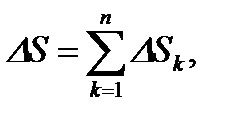
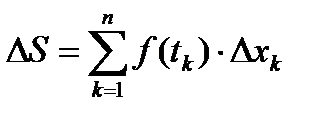
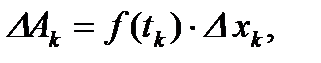
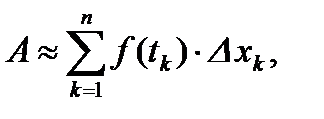
Определённый интеграл, основные свойства.
П.1. Разбиение отрезка.
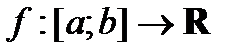
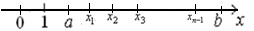
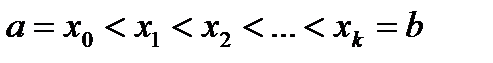
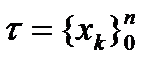 – разбиение отрезка
– разбиение отрезка 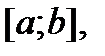
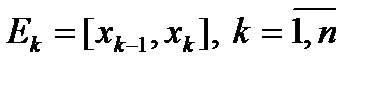 – частичные отрезки.
– частичные отрезки.
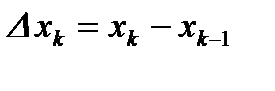 ,
, 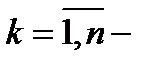 длина отрезка
длина отрезка 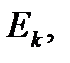
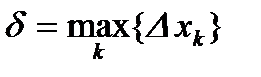 .
.
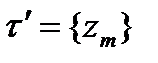 – новое разбиение отрезка
– новое разбиение отрезка 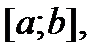 в состав которого входят все точки разбиения
в состав которого входят все точки разбиения 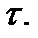
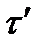 – продолжение разбиения
– продолжение разбиения 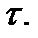
П.2. Понятие определённого интеграла.
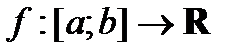
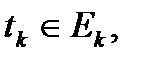
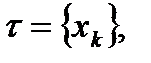
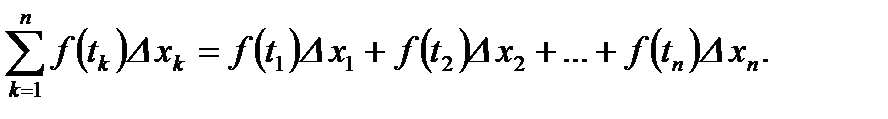
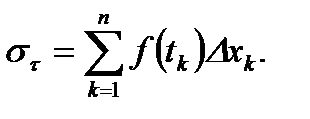 (1)
(1)
Сумму (1) будем называть интегральной суммой для функции 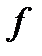 .
.
Определение 1. Число 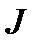 будем называть пределом интегральной суммы (1) при
будем называть пределом интегральной суммы (1) при 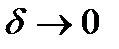 , если для
, если для 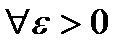
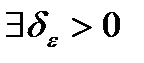 , что для всякого разбиения
, что для всякого разбиения 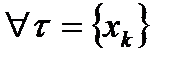 и для
и для 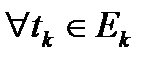 будем
будем 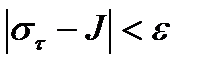 , если
, если 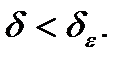
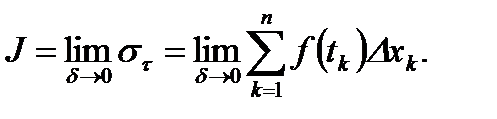 (2)
(2)
Определение 2. Если для 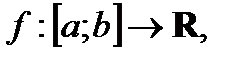 существует предел (2), то этот предел называется определенным интегралом (интегралом Римана) функции
существует предел (2), то этот предел называется определенным интегралом (интегралом Римана) функции 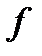 на
на 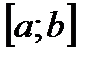 и обозначается
и обозначается
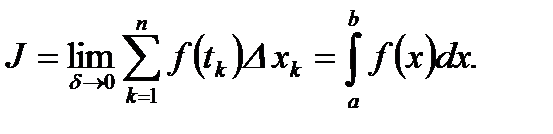 (3)
(3)
Функции, для которых существует (3), называются интегрируемыми по Риману на отрезке 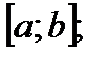 обозначается
обозначается 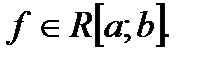
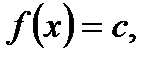
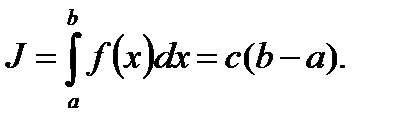
П.3. Необходимое условие интегрируемости.
Теорема 1. Чтобы функция f была интегрируемой на отрезке [a; b], необходимо, чтобы она на этом отрезке была ограничена.
|
|
|
Но это условие не является достаточным.
Например. 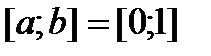
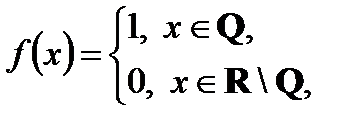 – функция Дирихле.
– функция Дирихле.
Такой интеграл не существует, функция не интегрируема по Риману, хотя и ограничена.
П.4. Критерий Коши.
Теорема 2.Функция f интегрируется по Риману тогда и только тогда, когда для 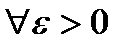
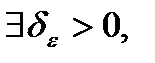 что для
что для 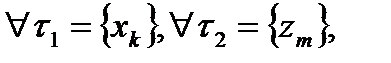
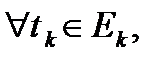
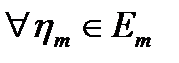 выполняется условие
выполняется условие 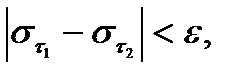 если
если 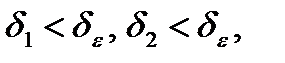 где
где 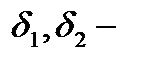 диаметры разбиений
диаметры разбиений 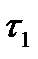 и
и 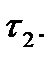
Доказательство.
1)Пусть 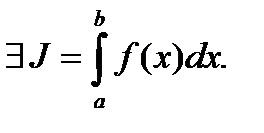
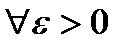
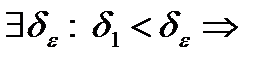
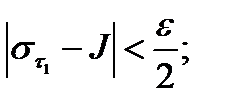
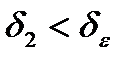
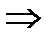
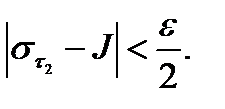
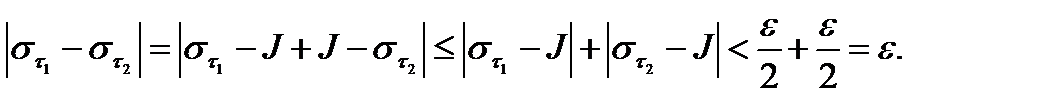
2) Пусть 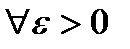
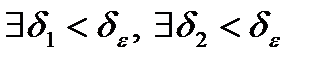
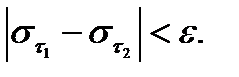 (*)
(*)
Функция 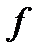 ограничена на
ограничена на 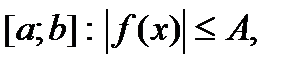 значит
значит 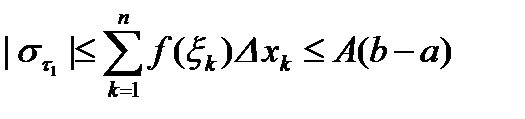 . Построим последовательность разбиений
. Построим последовательность разбиений 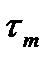 с диаметром
с диаметром 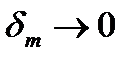 и рассмотрим последовательность интегральных сумм
и рассмотрим последовательность интегральных сумм 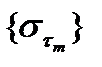 . Из условия (*) следует, что последовательность
. Из условия (*) следует, что последовательность 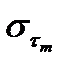 ограничена, т.е.
ограничена, т.е. 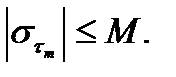 Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность. Не ограничивая общности рассуждений, будем считать
Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность. Не ограничивая общности рассуждений, будем считать 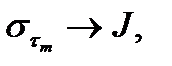 тогда имеем
тогда имеем
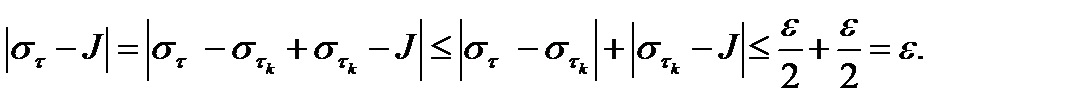
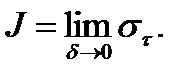 Критерий установлен.
Критерий установлен.
П.5. Достаточное условие интегрируемости.
Пусть 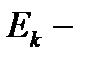 отрезки, полученные при разбиении отрезка
отрезки, полученные при разбиении отрезка 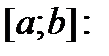
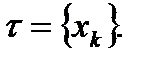
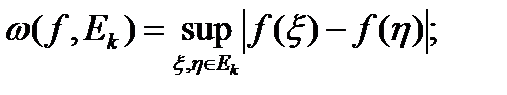
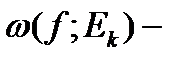 колебание функции
колебание функции 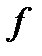 на
на 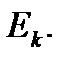
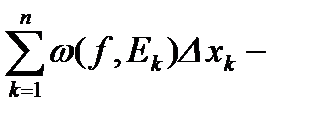 интегральное колебание функции
интегральное колебание функции 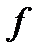 на
на 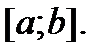
Теорема. Чтобы ограниченная на 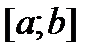 функция f была интегрируема на
функция f была интегрируема на 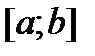 достаточно, чтобы
достаточно, чтобы 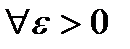
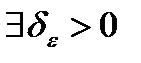 , что для
, что для 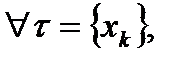
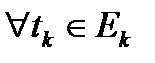 выполнялось условие
выполнялось условие 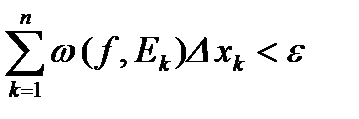 , если
, если 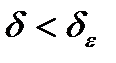 ,
, 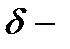 диаметр разбиения
диаметр разбиения 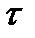 .
.
|
|
|
Доказательство. Пусть 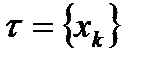 ,
, 
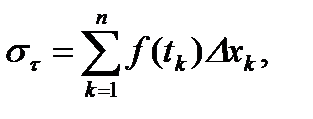
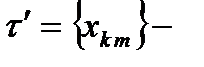 продолжение разбиения
продолжение разбиения 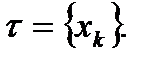
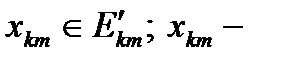 первый индекс означает, что точка лежит в отрезке
первый индекс означает, что точка лежит в отрезке 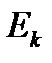 , а второй – номер точки на этом отрезке.
, а второй – номер точки на этом отрезке. 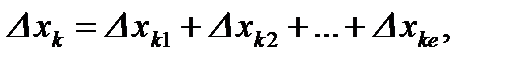
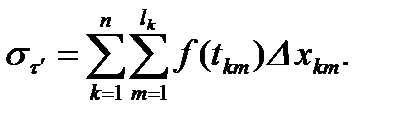
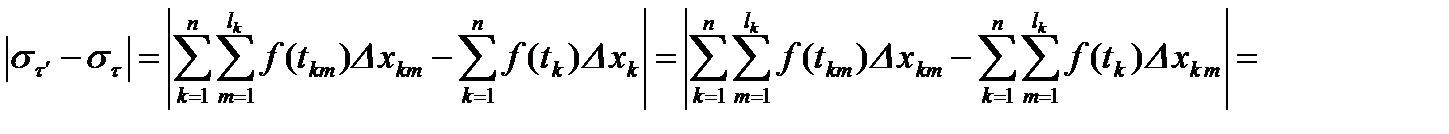
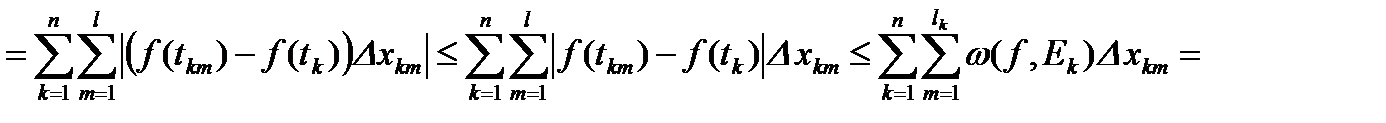
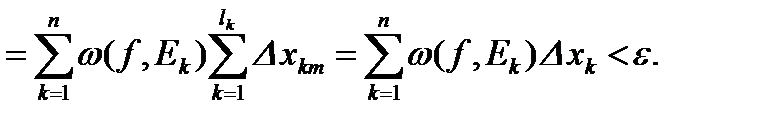
Рассмотрим теперь два произвольных разбиения 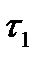 и
и 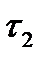 , диаметры которых
, диаметры которых 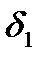 и
и 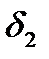 не превосходят
не превосходят 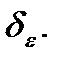 Пусть
Пусть 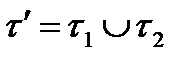 . Очевидно
. Очевидно  является продолжением разбиения
является продолжением разбиения 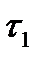 и
и 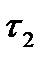 . Значит, имеем
. Значит, имеем
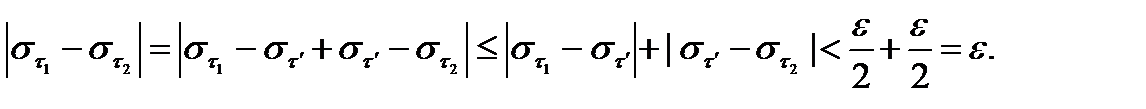
В силу критерия Коши 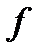 интегрируема на
интегрируема на 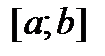 .
.
П.6. Классы интегрируемых по Риману функций.
Теорема 4. Если 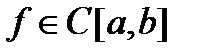 , то
, то 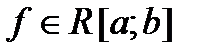 .
.
Доказательство. Так как 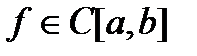 , то
, то  ,
, 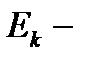 частичный отрезок разбиения
частичный отрезок разбиения 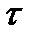 , значит f – равномерно непрерывна на отрезке
, значит f – равномерно непрерывна на отрезке 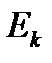 (теорема Кантора). Поэтому, можем сказать, что
(теорема Кантора). Поэтому, можем сказать, что 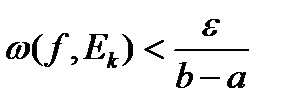 . Тогда имеем
. Тогда имеем
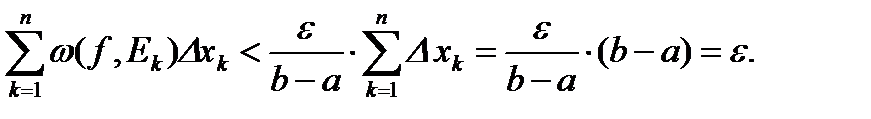
Теорема 5. Пусть функция f непрерывна на отрезке 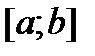 за исключением, быть может, точек
за исключением, быть может, точек 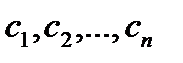 (конечного числа точек), если при этом f ограничена на отрезке
(конечного числа точек), если при этом f ограничена на отрезке 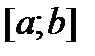 , то f интегрируема на
, то f интегрируема на 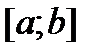 .
.
Теорема 6. Если f – монотонна на отрезке 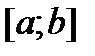 , то она на этом отрезке интегрируема.
, то она на этом отрезке интегрируема.
Доказательство этих теорем смотрите в [1].
Свойства интегралов.
П.1. Линейность.
Теорема 1. Имеет место
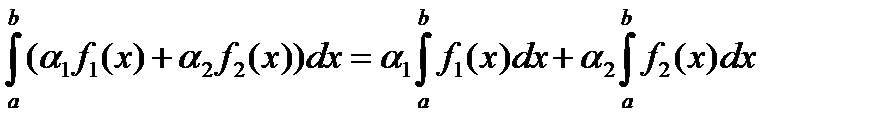 , где
, где 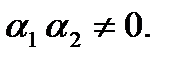 (1)
(1)
Доказательство.
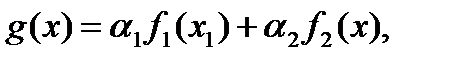
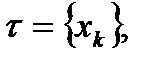
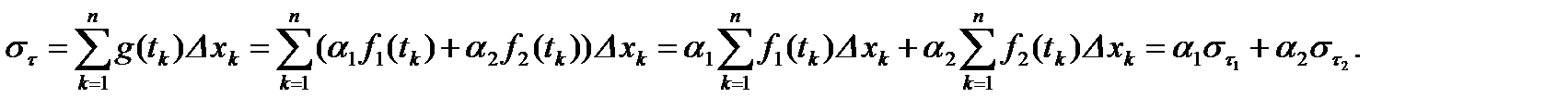
Значит 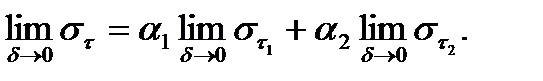
П.2. Монотонность.
Теорема 2. Пусть 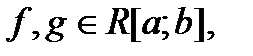
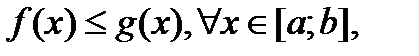 (2)
(2)
тогда
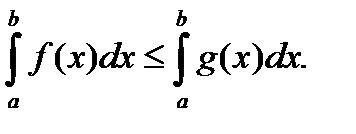 (3)
(3)
|
|
|
Следствие. (одна общая оценка интегралов)
Пусть 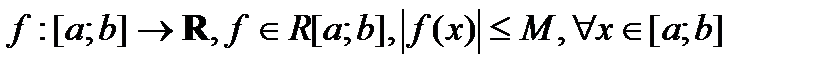 тогда
тогда
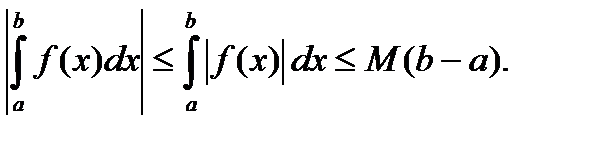 (5)
(5)
П.3. Аддитивность.
Определение.
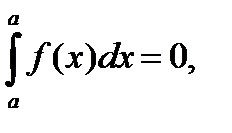
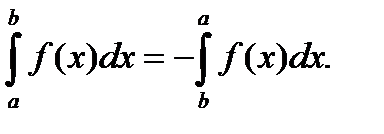
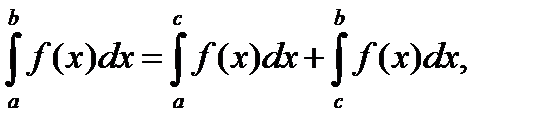
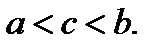 (6)
(6)

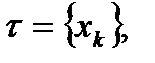
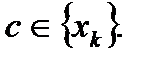
Следствие. 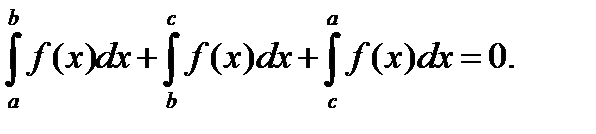
1) 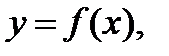
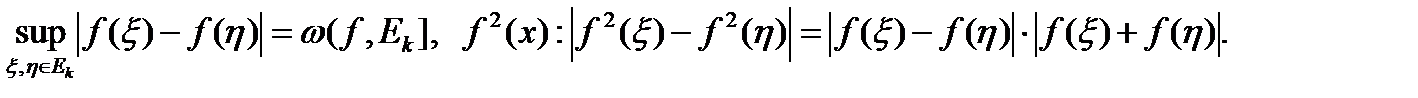
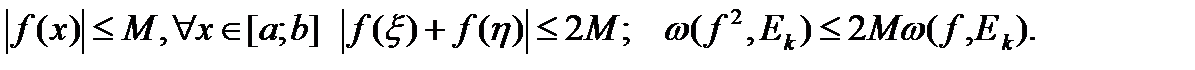
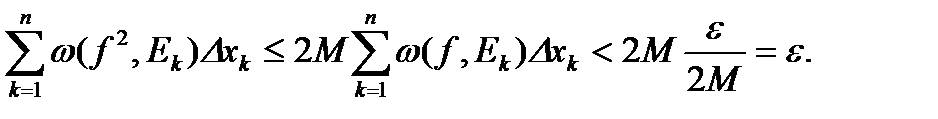

2) Пусть f и g – интегрируемы на 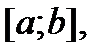 тогда
тогда 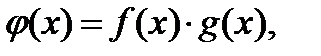
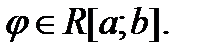
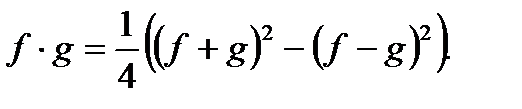
Интегралы от непрерывных функций.
П.1. Теоремы о среднем.
Теорема 1. Пусть 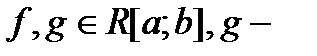 не меняет знака на
не меняет знака на 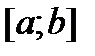 ;
; 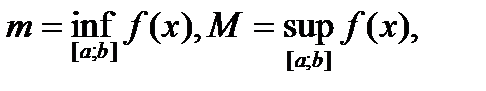 тогда
тогда 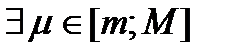 , что
, что
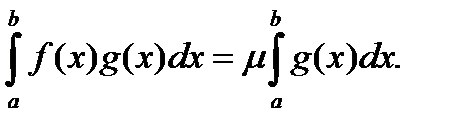 (1)
(1)
Следствие.
1) Если 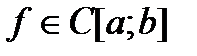 , то
, то
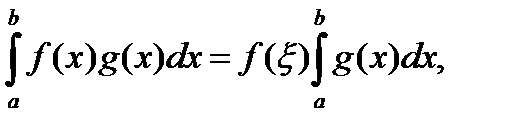
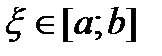 . (2)
. (2)
2) 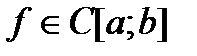
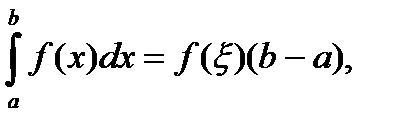
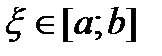 . (3)
. (3)
Доказательство. Считаем 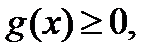
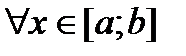 , имеем
, имеем 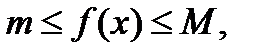
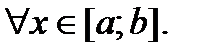
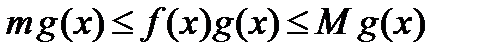 (4)
(4)
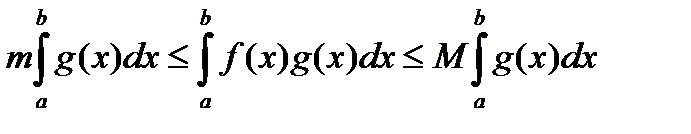 (5)
(5)
Если 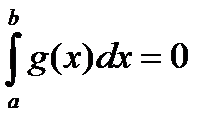 , то (5) очевидно и (1) имеет место. Пусть
, то (5) очевидно и (1) имеет место. Пусть 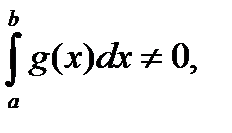 тогда из (5) получим
тогда из (5) получим
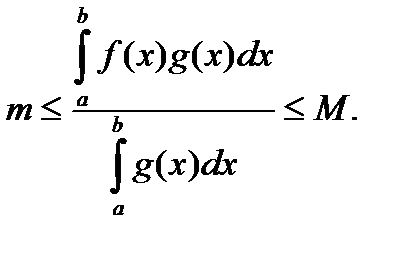 (6)
(6)
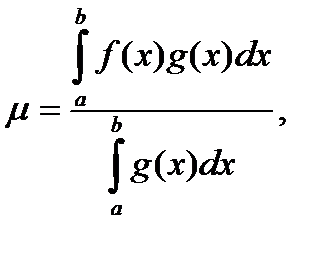
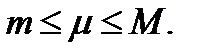
Следствие.
1) Если 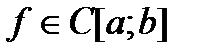 , тогда
, тогда 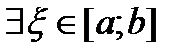 , что
, что 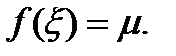
2) Если в (2) 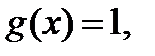 то
то 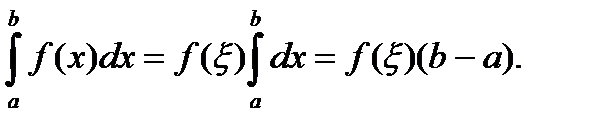
Теорема 2. (О среднем) Пусть f и g – интегрируемы на 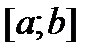 , g – монотонна на отрезке
, g – монотонна на отрезке 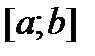 , тогда
, тогда
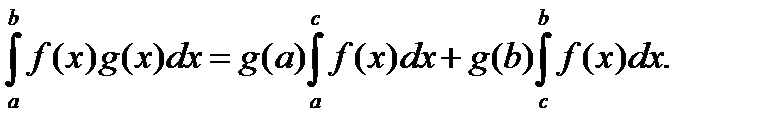
Дата добавления: 2018-08-06; просмотров: 225; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
