Уравнение поверхности и линии в пространстве
Геометрическое истолкование уравнений и неравенств с двумя переменными.
Введение системы координат на плоскости позволяет установить взаимно однозначное соответствие между множеством точек плоскости и множеством упорядоченных действительных чисел. Это соответствие позволяет задавать геометрические объекты с помощью ур-ий, нер-в или их систем и использовать при док-ве теорем или решений алгебраических задач.
Это существенно упрощает рассуждение и позволяет пользоваться определенными алгоритмами. В этом заключается суть метода координат. Для того, чтобы воспользоваться этим методом необходимо задавать геометрические объекты с помощью ур-ий или нер-в.
Фигуры на плоскости – мн-во точек. Рассмотрим исходную фигуру Ф на пл-ти, где задана АСК.
Условием, определяющим фигуру Ф в данной системе координат наз-сяур-иенер-ва или их система, в которой удовлетворяют координаты точек фигуры Ф и не удовлетворяет координатыточек, не принадлежащих фигуре Ф.
Условиек, определяющее фигуру Ф, наз-ся уравнением фигуры Ф в системе координат. При решении геометрических объектов методом координат часто решаются 2 задачи.
1 задача: фигура Ф задана как мн-во точек, обладающих некоторым свойством. Требуется найти аналитическое условие, определяющее эту фигуру, т.е. составить ее ур-ие.
2 задача: задано аналитическое условие, определяющее фигуру, требуется выяснить геометрические свойства этой фигуры.
|
|
|
При изучении метода координат в кач-ве фигур чаще всего рассматриваются линии: прямая, окружность , синусоида и т.д.. Условием, определяющим линию в АСК является уравнение F(x,y)=0. Изучение линий и решение задач с ними является предметом аналитической геометрии.
Алгоритм решения задач 1 типа.
Дано: некоторая линия, заданная как м-во точек, обладающая характеристическим свойством.
Найти: уравнение этой линии.
Алгоритм: 1) выбираем систему координат С1К1
2) Выбираем точку М1, принадлежащую нашей линии и обозначаем координаты точки М(х, у)
3) характер.св-во записываем с помощью координат. Получаем зависимость между Х и У произвольной точки линии. Эта зависимость является ур-ием, которое удовлетворяет точки линии.
4) упрощаем ур-ие, если возможно, делая равносильные переходы.
5) доказываем, что полученное ур-ие – это ур-ие гамма (  . Доказываем , что , если координаты (х,у) удовлетворяют уравнению, то точка М принадлежит
. Доказываем , что , если координаты (х,у) удовлетворяют уравнению, то точка М принадлежит 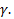
Пример 1. Окружность – мн-во точек плоскости, равноудаленных от точки С на расстояние R. РИСУНОК
1.Выбираем декартову систему координат С(х0, у0)
2.Точка М (х,у) 
3. |CM| =R 
4. 
5. M  N
N  |CN|
|CN| 
С(0,0)  – каноническое ур-ие окружности
– каноническое ур-ие окружности
|
|
|
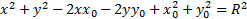
 , где (
, где (  -2x0=A, -2y0=B)
-2x0=A, -2y0=B)

При любых значениях А, В,С, - это уравнение окружности ?

1. 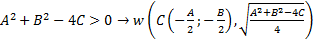
2. 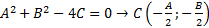
3. 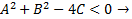 не имеет смысла в действительных числах.
не имеет смысла в действительных числах.
Пример 2. Найти аналитические условия, которые определяет фигура. РИСУНОК
1.ПДСК
2.М(х,у) 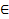 F (фигура)
F (фигура)
3. 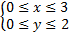
5. N  , значит , она не попадает хотя бы в 1 полосу. Следовательно, ее координаты не будут удовлетворять нашему ур-ию.
, значит , она не попадает хотя бы в 1 полосу. Следовательно, ее координаты не будут удовлетворять нашему ур-ию.
Задача 2’. 1. АСКРИСУНОК
2. .М(х,у) 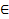 F
F
3. 
4, 5 пункт см.выше
3 пример. ху=0 а в АСК РИСУНОК
М-(х,у) х=0 или у= 0
 пара пересекающихся прямых
пара пересекающихся прямых
4 пример. рассмотрим фигуры в ПДСК
А)р=3 РИСУНОКб)  РИСУНОК в)
РИСУНОК в)  РИСУНОК
РИСУНОК
Пример 5. Отрезок постоянной длины скользит своими концами по сторонам прямого угла. Из вершины прямого угла проведен перпендикуляр к этому отрезку. Найти геометрическое место точек оснований этих перпендикуляров .РИСУНКИ
Выберем ПСК так, чтобы вершина угла ….
1.ПСК 0-полюс
2.М( 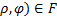
3. 

Алгебраическая линия и ее порядок.
Линия на плоскости определяется на плоскости f(x,y)=0 отношению двух переменных относительно АСК. Это означает, что координаты точки, принадлежащей линии удовлетворяют этому уравнению.
Определение. Линия на плоскости наз-ся алгебраической, если в некоторой АСК она задается ур-иемf(x,y)=0, где f(x,y) – это многочлен относительно х , у
|
|
|
Многочлен f(x,y) состоит из вида axsyp, где а – действительное число, sиp– целыне положительные числа.
Число s+p – наз-ся степенью одночлена. Наибольшая степень s+p – это степень многочлена.
Степень многочлена f(x,y) наз-ся порядком линии заданным ур-иемf(x,y)=0.
Теорема. Порядок алгебраической линии не зависит от выбора АСК. Док-во: пусть в данной АСК (0; 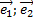 ) ур-ие линии f(x,y)=0, где f(x,y) – многочлен, состоящий из одночленов axsyp, где s+p
) ур-ие линии f(x,y)=0, где f(x,y) – многочлен, состоящий из одночленов axsyp, где s+p 
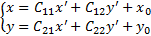

Получится новое:g(x’, y’,)=0  . Степень многочлена gувеличиваться не может, но может уменьшаться. При обратном переходе степень повыситься не может. Вывод: они равны.
. Степень многочлена gувеличиваться не может, но может уменьшаться. При обратном переходе степень повыситься не может. Вывод: они равны.
Прямая.
Любой ненулевой вектор параллельный прямой наз-ся направляющим вектором этой прямой.
Любая прямая на плоскости в АСК может быть задана одним из след.образов:
1)точка и направляющий вектор
2) 2 точки.
Задача 1. Напишем ур-ие прямой по точке и направляющему вектору. РИСУНОК
1 способ. 1.АСК A(x0, y0) 
2.M(x,y) 
3.  –каноническое ур-ие прямой
–каноническое ур-ие прямой
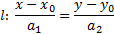
a2(x-x0)=a1(y-y0)
a2x-a2x0= a1y -a1y0
5. 
2 способ.1.АСКA(x0, y0) 
2.M(x,y) 
3. 
4.  – параметрические уравнения прямой.
– параметрические уравнения прямой.
5. . 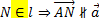
3 способ. Рассмотрим каноническое ур-ие.
a2(x-x0)=a1(y-y0) 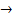 a2x-a2x0= a1y -a1y0
a2x-a2x0= a1y -a1y0 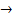 a2x-a2x0-a1y -a1y0=0
a2x-a2x0-a1y -a1y0=0 
a:Ax+By+C=0, гдеA=a2, B=a2, C=a1y0+a2x0– общееуравнениепрямой
|
|
|
Прямая – алгебраическая линия первого порядка.
Теорема. Линия на плоскости в АСК заданная уравнением Ах+Ву+С=0 задает прямую с направляющим вектором. 
М0(х0,у0)  A
A  +B
+B  +C=0
+C=0 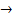 С =-A
С =-A  -B
-B 
 - A
- A  - B
- B  А(x-x0)+В(y-y0)=0
А(x-x0)+В(y-y0)=0 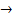 А(x-x0)= - В(y-y0)
А(x-x0)= - В(y-y0)
Это каноническое уравнение прямой, проходящей через точку с координатами х0, у0 в направлении 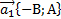 . любое уравнение 1 степени задает прямую.
. любое уравнение 1 степени задает прямую.
Задача 2.Напишем уравнение прямой по двум точкам. РИСУНОК
1.АСКA(x1, y1)В(x2, y2)
2. M(x,y) 
3. 
 – уравнение по двум точкам.
– уравнение по двум точкам.
Задача 3. Уравнение с угловым коэффициентом. Рассмотрим прямую 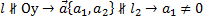 . Число
. Число  равное отношению наз-сякоэффициентом прямой
равное отношению наз-сякоэффициентом прямой
a2(x-x0)=a1(y-y0) : а1

 - уравнение с угловым коэффициентом
- уравнение с угловым коэффициентом

Аналитическое условие определяющее полуплоскость.
Пусть в АСК на плоскости задана ур-ием прямая:  . Эта прямая разбивает плоскость на две полуплоскости.
. Эта прямая разбивает плоскость на две полуплоскости.
Теорема. Если на плоскости в АСК прямая  задана своим общим ур-ием
задана своим общим ур-ием  , то нер-во
, то нер-во  задают полуплоскость, ограниченную этой прямой. РИСУНОК
задают полуплоскость, ограниченную этой прямой. РИСУНОК
 составим определитель этих координат
составим определитель этих координат
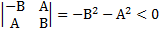
2)  M(x,y)
M(x,y)
3) 

 + B
+ B  +A
+A 
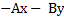 -С
-С 

Пример: задана прямая  уравнением
уравнением 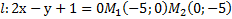 пересекает ли она отрезок с концами
пересекает ли она отрезок с концами  ? РИСУНОК
? РИСУНОК
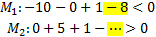
Уравнение поверхности и линии в пространстве
Задание АСК в пространстве устанавливает взаимно однозначное соответствие между точками пространства и упорядоченными тройками действительных чисел их координат.
Это соответствие позволяет задавать геометрические фигуры в пространстве с помощью уравнений неравенств или их систем.
Пусть в пространстве задана некоторая АСК и фигура F.
Условием, определяющим фигуру Fв заданной АСК называется уравнение, неравенство или их система, которым удовлетворяют координаты точек, не принадлежащих этой фигуре F.
Условием, определяющее фигуры Fназывается уравнением этой фигуры в данной АСК.
Пример. Z=0 – плоскость Оху .z  0 – полупространство
0 – полупространство
 -окружность в плоскости Оху.
-окружность в плоскости Оху.
При изучении фигур методом координат чаще всего рассматриваются поверхности : плоскость, сфера, т.д.
Уравнение поверхности в АСК: F (x,y,z)=0
В пространстве, как и на плоскости решаются задачи 2 типов:
1.По характеристическому св-ву определить тип уравнения
2.По уравнению определить св-ва точек фигур.
Схема решения задач та же
Пример. R,C(a,b,c)описать ур-ие сферы с радиусом Rи центром C(a,b,c).
1.ПДСК, C(a,b,c).
2.M(x,y,z) 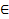 S -сфера
S -сфера
3. |CM|=R 
4. 
5. 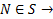 |CN|
|CN|  и ее координаты не будут удовлетворять нашему уравнению
и ее координаты не будут удовлетворять нашему уравнению
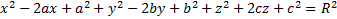 (следует из 4 пункта, раскрыв скобки; где
(следует из 4 пункта, раскрыв скобки; где  )
)

D= 
Аналогично можно показать, что это уравнение не всегда определяет сферу.
Как определить линию в пространстве?
Линию можно получить, как мн-во точек пересечения двух поверхностей :

Если есть поверхность 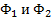 , то тогда
, то тогда 
В аналогичной ситуации с плоскостью вводятся определения алгебраической поверхности и ее порядка.
Дата добавления: 2018-08-06; просмотров: 436; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
