Сложение положительных рациональных чисел коммутативно и ассоциативно,
Понятие обыкновенной дроби; понятие положительного рационального числа. Множество положительных рациональных чисел как расширение множества натуральных чисел.
Пусть даны отрезок х и единичный отрезок е, длина которого Е. Если отрезок х состоит из т отрезков, равных п-ой части отрезка е, то длина отрезка х может быть представлена в виде 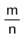 Е, где символ — называют дробью (и читают «эм энных»).
Е, где символ — называют дробью (и читают «эм энных»).
В записи дроби 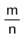 числа m и n - натуральные, m называется числителем, n - знаменателемдроби.
числа m и n - натуральные, m называется числителем, n - знаменателемдроби.
Дробь 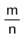 называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателяилиравен ему.
называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателяилиравен ему.
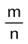 Для того чтобы дроби
Для того чтобы дроби 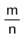 и
и 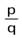 выражали длину одного того же отрезка, необходимо и достаточно, чтобы выполнялось равенство тq = nр.
выражали длину одного того же отрезка, необходимо и достаточно, чтобы выполнялось равенство тq = nр.
Две дроби и 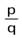 называются равными, если тq = пр.
называются равными, если тq = пр.
Если дроби равны, то пишут 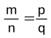
Теорема.Равенство дробей является отношением эквивалентности.
Доказательство. Действительно, равенство дробей рефлексивно: 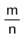 =
= 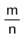 ,так как равенство mn = nm справедливо для любых натуральных чисел n и m.
,так как равенство mn = nm справедливо для любых натуральных чисел n и m.
Равенство дробей симметрично: если 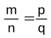 , то
, то 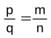 , так как из mq = nр следует, что рn = qm (m, n, р, qÎN ). Оно транзитивно: если
, так как из mq = nр следует, что рn = qm (m, n, р, qÎN ). Оно транзитивно: если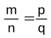 и
и 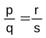 , то
, то 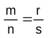 .В самом деле, так как
.В самом деле, так как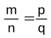 ,то mq = nр, а так как
,то mq = nр, а так как 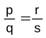 , то рs = qr. Умножив обе части равенства mq = nр на s, а равенства рs = qr на n, получим mqs = nрs и nрs = qrs. Откуда mqs =qrn или ms = nr. Последнее равенство означает, что
, то рs = qr. Умножив обе части равенства mq = nр на s, а равенства рs = qr на n, получим mqs = nрs и nрs = qrs. Откуда mqs =qrn или ms = nr. Последнее равенство означает, что 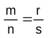 . Итак, равенство дробей рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.
. Итак, равенство дробей рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.
|
|
|
Из определения равных дробей вытекает основное свойство дроби. Напомним его.
Основное свойство дроби. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.
На этом свойстве основано сокращение дробей и приведение дробей к общему знаменателю.
Сокращение дробей - это замена данной дроби другой, равной данной, но с меньшим числителем и знаменателем.
Если числитель и знаменатель дроби одновременно делятся только на единицу,то дробь называют несократимой.
Положительным рациональным числом называется класс равных дробей, а каждая дробь, принадлежащая этому классу, есть запись (представление) этого числа.
Например, множество дробей 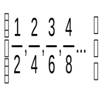 - это один класс, множество дробей
- это один класс, множество дробей 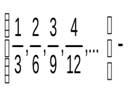 это другой класс и т.д.
это другой класс и т.д.
Дроби одного класса выражают длину одного и того же отрезка. Но длина отрезка должна представляться единственным числом. Поэтому считают, что равные дроби - это различные записи одного и того же положительного рационального числа.
Положительным рациональным числом называется класс равных дробей, а каждая дробь, принадлежащая этому классу, есть запись (представление) этого числа.
|
|
|
Например, о дроби 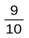 мы должны говорить, чтоона является записью некоторого рационального числа. Однако часто для краткости говорят
мы должны говорить, чтоона является записью некоторого рационального числа. Однако часто для краткости говорят 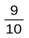 : - это рациональное число
: - это рациональное число
Множество всех положительных рациональных чисел принято обозначать символом Q+. Определим на этом множестве отношение равенства.
Определение.Если положительное рациональное число а представлено дробью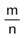 , а положительное рациональное число b другой дробью
, а положительное рациональное число b другой дробью 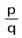 , то а = b тогда и только тогда, когда тq = nр.
, то а = b тогда и только тогда, когда тq = nр.
Если положительное рациональное число а представлено дробью 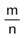 , а положительное рациональное число b - дробью
, а положительное рациональное число b - дробью 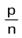 ,то их суммой называется число а + b, которое представляется дробью
,то их суммой называется число а + b, которое представляется дробью 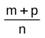 , т.е.
, т.е. 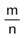 +
+ 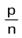 =
= 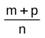 (1)
(1)
В определении суммы рациональных чисел мы использовали их представления в виде дробей с одинаковыми знаменателями. Если же числа а и b представлены дробями с различными знаменателями, то сначала надо привести их к одному знаменателю, а затем применять правило (1).
Сложение положительных рациональных чисел коммутативно и ассоциативно,
("а, b Î Q+) а + b= b + а;
("а, b, с Î Q+) (а + b)+ с = а + (b+ с)
Если положительное число а представлено дробью 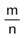 , а положительное рациональное число b дробью
, а положительное рациональное число b дробью 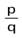 , то их произведением называется число а b , которое представляется дробью
, то их произведением называется число а b , которое представляется дробью 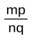 .
.
|
|
|
Определение сложения положительных рациональных чисел дает возможность определить отношение «меньше» на множествеQ+.
Определение. Пусть а и b - положительные рациональные числа. Считают, что число b меньше числа а, если существует такое положительное рациональное число с, что а= b + с.
В этом же случае считают, что число а больше числа b. Пишут b < а, а> b.
Так определенное отношение «меньше» обладает рядом свойств, которые мы приводим без доказательства.
1. Отношение «меньше» на множестве Q+ антисимметрично и транзитивно, т.е. является отношением порядка, а множество Q+ упорядоченным множеством.
2. Если рациональные числа а и b представлены дробями 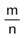 и
и 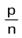 (т.е. дробями, имеющими одинаковые знаменатели), то а < b в том и только в том случае, когда m < р.
(т.е. дробями, имеющими одинаковые знаменатели), то а < b в том и только в том случае, когда m < р.
3. Если рациональные числа а и b представлены дробями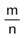 и
и 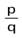 (т.е. дробями, имеющими разные знаменатели), то а <b в том и только в том случае, когда т q < nр.
(т.е. дробями, имеющими разные знаменатели), то а <b в том и только в том случае, когда т q < nр.
4. В множестве положительных рациональных чисел нет наименьшего числа.
5. Между любыми двумя различными числами а и b из Q+ заключено бесконечно много чисел этого же множества. Это свойство называют свойством плотности множества Q+.
|
|
|
6. В множестве положительных рациональных чисел нет наибольшего числа.
Вычитание положительных рациональных чисел определяется как операция, обратная сложению, т.е. это такая операция, которая удовлетворяет условию: а - b = с тогда и только тогда, когда а = b + с.
Разность а - b положительных рациональных чисел существует тогда и только тогда, когда b < а. Если разность а - b существует, то она единственна.
Используя определение и условие существования разности, можно получить правило вычитания положительных рациональных чисел,представленных дробями 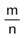 и
и 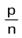 , где т < р :
, где т < р : 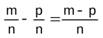 /
/
Деление положительных рациональных чисел определяется как операция, обратная умножению, т.е. это такая операция, которая удовлетворяет условию: а:b=с тогда и только тогда, когда а = bс.
Из этого определения и правила нахождения произведения положительных рациональных чисел можно получить правило деления положительных рациональных чисел, представленных дробями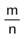 и
и 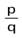 :
: 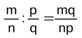 .
.
Из этого правила следует, что частное положительных рациональных чисел всегда существует.
Множества натуральных чисел
Чтобы множество Q+ положительных рациональных чисел являюсь расширением множества N натуральных чисел, необходимо выполнение ряда условий.
Первое условие- это существование между N иQ+ отношения включения. Докажем, что
N ÌQ+.
Пусть длина отрезка х при единичном отрезкеевыражается натуральным числомm. Разобьем единичный отрезок направных частей. Тогдаn-ая часть единичного отрезка будет укладываться в отрезке Х точноmпраз, т.е. длина отрезкахбудет выражена дробью 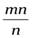 . Значит, длина отрезках выражается и натуральным числомm, и положительным рациональным числом
. Значит, длина отрезках выражается и натуральным числомm, и положительным рациональным числом 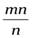 . Но это
. Но это
должно пбыть одно и то же число. Поэтому целесообразно считать, что дроби вида 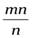 являются записями натурального числаm.
являются записями натурального числаm.
Следовательно, N ÌQ+.
Так, например, натуральное число 6 можно представить в виде следующих дробей: 6/1 12/2, 18/3 24/4, 30/5 и т.д.
Отношение между множествами N и Q+ представлено на рисунке 129.

Рисунок 129.
Числа, которые дополняют множество натуральных чисел до множества положительных рациональных, называются дробными.
Второе условие, которое должно быть выполнено при расширении множества натуральных чисел, - это согласованность операций, т.е. результаты арифметических действий, произведенных по правилам, существующим для натуральных чисел, должны совпадать с результатами действий над ними, но выполненных по правилам, сформулированным для положительных рациональных чисел. Нетрудно убедиться в том, что и это условие выполняется.
Пусть аиb- натуральные числа,а+b- их сумма, полученная по правилам сложения в N. Вычислим сумму чиселаиbпо правилу сложения вQ+. Так как а = 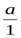 ,b=
,b= 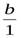 , то
, то 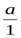 +
+ 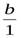 =
= 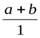 =а+bУбедиться в том, что второе условие выполняется и для других операций, можно аналогично.
=а+bУбедиться в том, что второе условие выполняется и для других операций, можно аналогично.
Третье условие, которое должно быть выполнено при расширении множества натуральных чисел - это выполнимость вQ+операции, не всегда осуществимой вN. И это условие соблюдено: деление, которое не всегда выполняется в множествеN, в множествеQ+выполняется всегда.
Сделаем еще несколько дополнений, раскрывающих взаимосвязи между натуральными и положительными рациональными числами.
1. Черту в записи дроби 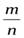 — можно рассматривать как знак деления.
— можно рассматривать как знак деления.
Действительно, возьмем два натуральных числа mиnи найдем их частное по правилу (4) деления положительных рациональных чисел:
m:n = 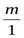 :
: 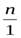 =
= 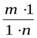 =
= 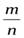 .
.
Обратно, если дана дробь 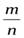 , то ее можно рассматривать как частое натуральных чиселmиn:
, то ее можно рассматривать как частое натуральных чиселmиn:
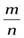 =
= 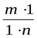 =
= 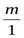 :
: 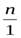 = m:n.
= m:n.
2. Любую неправильную дробь можно представить либо в виде натурального числа, либо в виде смешанной дроби.
Пусть 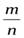 - неправильная дробь. Тогдаm>n. Еслиmкратноn, то в этом случае дробь
- неправильная дробь. Тогдаm>n. Еслиmкратноn, то в этом случае дробь 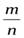 является записью натурального числа. Если числоm не кратноn, то разделимm наnс остатком:
является записью натурального числа. Если числоm не кратноn, то разделимm наnс остатком:
m=nq + r, гдеr<n.
Подставим nq + rвместоmв запись 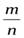 и применим правило (1) сложения положительных рациональных чисел:
и применим правило (1) сложения положительных рациональных чисел: 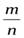 =
= 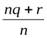 =
= 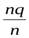 +
+ 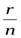 =q+
=q+ 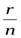 .
.
Так как r<n, то дробь 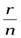 - правильная. Следовательно, неправильная дробь — оказалась представленной в виде суммы натурального числаqи правильной дроби
- правильная. Следовательно, неправильная дробь — оказалась представленной в виде суммы натурального числаqи правильной дроби 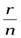 . Это действие называется
. Это действие называется
выделением целой части из неправильной дроби. Например, 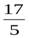 =
= 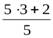 =
= 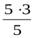 +
+ 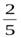 =3+
=3+ 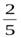 .
.
Сумму натурального числа и правильной дроби принято записывать без знака сложения: т.е. вместо
3 + 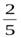 пишут 3
пишут 3 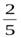 и называют такую запись смешанной дробью.
и называют такую запись смешанной дробью.
Справедливо также утверждение: всякую смешанную дробь можно записать в виде неправильной дроби. Например:
3 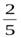 =3+
=3+ 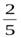 =
= 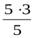 +
+ 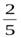 =
= 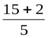 =
= 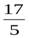 .
.
Дата добавления: 2018-08-06; просмотров: 1958; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
