Метод векторных диаграмм и комплексные обозначения

⇐ ПредыдущаяСтр 3 из 3

1. Существует наглядный геометрический способ представления гармонических колебаний. Допустим, что геометрическая точка М равномерно вращается по окружности радиуса г (рис. 299) с угловой скоростью со0. Положение точки на окружности можно задать центральным углом ф между радиусом ОМ и положительным направлением оси X. Он равен ф = a>0t + б, где б — значение угла ф в начальной момент t = 0. При вращении точки М ее проекция N на ось X двигается по диаметру АВ туда и обратно, совершая колебания между точками Л и б с периодом Т0 = 2я/о>„. Абсцисса точки N

х = асо$ ф = асо8 (оу + б), (126.1)

как и сама точка N, совершает незатухающее гармоническое колебание. Этим способом можно представлять гармонические колебания любых величин. Надо только условиться изображать колеблющуюся величину абсциссой точки М, равномерно вращающейся по окружности. Вместо абсциссы можно, конечно, брать ординату y = asin (co0/ + S) = acosj^o0/ + f6 — yjj, но во избежание недоразумений условимся всюду пользоваться абсциссой.

Для представления затухающих колебаний вместо окружности надо взять логарифмическую спираль, асимптотически приближающуюся к фокусу О (рис. 300). Если точка М движется по спирали с постоянной угловой скоростью со0, приближаясь к фокусу, то ее проекция N на ось X будет совершать затухающее гармоническое колебание-

	У


		Л? 1]
ч	О	® NJB К

Рис299 ,рис300(снизу)

У ( ( W	\ /v\ \	«М
	h h х

2. Вместо точки М можно взять радиус-вектор г = ОМ, равномерно вращающийся вокруг начала координат О. Гармонически колеблющаяся величина изобразится проекцией х этого радиуса- вектора на ось X. При этом во многих задачах оказывается удобным математические операции над величиной х заменить соответствующими операциями над самим радиусом-вектором г. Например, если нужно вычислить сумму слагаемых

Xi = cos (со,/4-бх) и х-2 = аге~ ъ* cos (ю2< + 6г).

то можно сначала сложить по правилу параллелограмма векторы гх и г2, проекциями которых являются эти слагаемые, а затем спроектировать полученный вектор г = гх + г2 на ось абсцисс. Результат этих операций, очевидно, будет равен х = хх + х2. Операция проектирования производится в самом конце вычисления. При известном навыке можно совсем отвлечься от проекций, а изображать колеблющуюся величину непосредственно самим вектором г, равномерно вращающимся вокруг своего начала.

Его проектирование на ось X подразумевается, но не выполняется фактически. Такой метод называется методом векторных диаграмм. Рис. 299 можно поэтому назвать векторной диаграммой незатухающего, а рис. 300 — затухающего гармонического колебания. Метод векторных диаграмм широко применяется в электротехнике при изучении переменных токов.

3. В физике более широкое распространение получил другой метод, отличающийся от метода векторных диаграмм только по форме. В этом методе колеблющаяся величина представляется комплексным числом. Положение точки на плоскости (рис. 299) можно однозначно задать комплексным числом z = х -f iy. Если точка М вращается, то

x = acos (ti>0t-{-8), у —asm (оУ + б). Поэтому, используя известную формулу Эйлера

e"t = cos ф + t sin ф, величину z можно представить в виде

Вещественная часть этого выражения

Re (г) = a cos (w0t -f 6) = х

представляет гармонические колебания величины х. Условимся опускать знак взятия вещественной части Re и писать просто

х = аеЧ**+й\ (126.2)

Это символическое равенство не следует понимать буквально. Его надо понимать в том смысле, что физическая величина х равна вещественной части комплексного выражения, стоящего в этом равенстве справа. Модуль этого комплексного выражения а равен амплитуде колебания, а его аргумент a>0t + б — фазе. Можно формально упростить запись (126.2). Введем комплексную величину А = aeib, называемую комплексной амплитудой колебания. Тогда

х = Ае<«>°'. (126.3)

Комплексность амплитуды А означает, следовательно, что колебание происходит с начальной фазой, отличной от нуля.

Наконец, можно формально рассматривать выражения типа (126.3) при комплексных значениях величины со0. Для раскрытия физического смысла таких выражений полагаем со0 = сох + 1Щ- Тогда

x = Aei + '0)2)' = ае~ + в) == ае~ «>•-' cos (о)х/ + б).

Если оь > 0, то это выражение представляет затухающее гармоническое колебание с круговой частотой сох и показателем затухания (о2. Если (оа < 0, то получится колебание с неограниченно нарастающей амплитудой. Таким образом, если частота комплексна, то это означает, что амплитуда колебания экспоненциально затухает или нарастает во времени.

Очень важно научиться понимать физический смысл уравнений, записанных в комплексной форме, не переходя к вещественной форме записи. Комплексная форма позволяет часто избежать громоздкости формул и делает сами формулы более общими и легче обозримыми. Особенно широко комплексная форма применяется при изучении распространения волн.

7)Сложение двух гармонических колебаний одинакового направления и одной частоты

При сложении двух гармонических колебаний одинакового направления и частоты, результирующее смещение будет суммой ( ) смещений и , которые запишутся следующими выражениями:

, ,
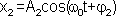Сумма двух гармонических колебаний также будет гармоническим колебанием той же круговой частоты:
= .
Значения амплитуды А и начальной фазы φ этого гармонического колебания будет зависеть от амплитуд исходных колебаний и их начальных фаз (Рис. 1.2).

Рисунок 1.2. Сложение двух гармонических колебаний одинакового направлени частоты

На рисунке 1.2. приведено два примера А и В сложения гармонических колебаний с использованием метода векторных диаграмм.Из векторных диаграмм видно, что направление (начальная фаза φ) и длина А вектора амплитуды суммарного гармонического колебания зависит, как от направления (от начальных фаз), так и от длины векторов амплитуд исходных гармонических колебаний.
Если угол (разность фаз: Δφ = φ1 - φ2) между векторамиА1 и А2 равен 0, то исходные колебания находятся вфазе и суммарная амплитуда (А =А1 +А2) будет максимальна. Если угол (разность фаз: Δφ = φ1 - φ2) между векторамиА1 и А2 равен - π или π, то исходные колебания находятся в противофазеи суммарная амплитуда (А = А1 -А2 ) будет минимальна.

8)Сложение двух гармонических колебаний с неодинаковыми частотами.(Биения и модуляции)

Если частоты колебаний и , неодинаковы, векторы А1 и А2 будут вращаться с различной скоростью. В этом случае результирующий вектор А пульсирует по величине и вращается с не постоянной скоростью. Результирующим движение уже будет не гармоническое колебание, а сложный колебательный процесс.

Биения Биения возникают при сложении колебаний, отличающихся по частоте на небольшую величину, и проявляются в появлении более низкочастотных изменений амплитуды суммарного сигнала, по сравнению с исходными частотами. Амплитуда колебаний при этом меняется от минимального значения равного разности исходных амплитуд до максимального значения, равного сумме амплитуд исходных колебаний, и вновь до минимального значения. Периодом биений является время повторения этого процесса (Рис 1.3.).

Рисунок 1.3.

За счет того, что вращение векторов А1 и А2 происходит с близкими, но отличающимися скоростями, разность фаз этих двух колебаний будет не постоянна, а медленно, то увеличиваться, то уменьшаться. Колебания будут находиться, то в фазе, то в противофазе, в результате амплитуда суммарного сигнала тоже будет меняться. Время за которое разность фаз измениться на 2π и будет периодом биений Тб (Тб = 2π/Δω). Δω -разность круговых частот исходных колебаний.
Биения применяют при обнаружении металлических предметов мин, оружия и т.д.

Дата добавления: 2018-08-06; просмотров: 376; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 23

Мы поможем в написании ваших работ!