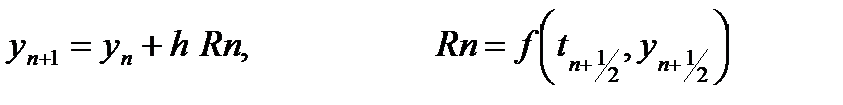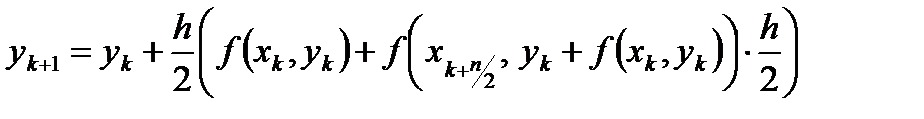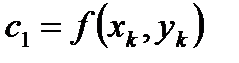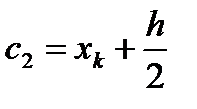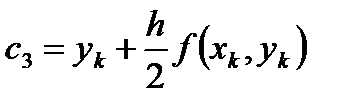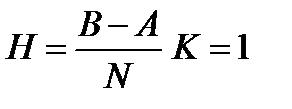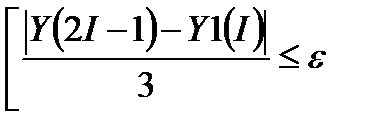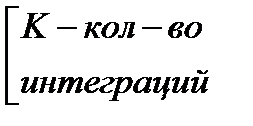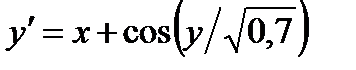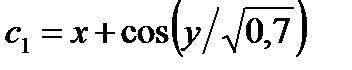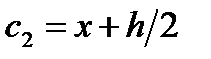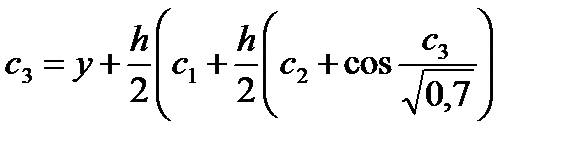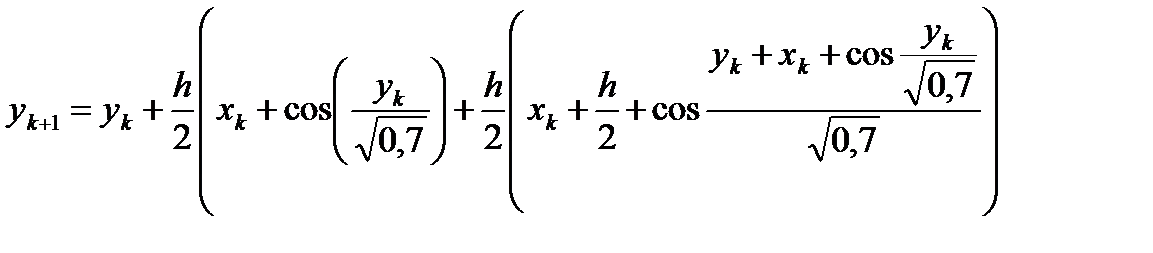Модификации метода Эйлера второго порядка точности
Медленная сходимость метода Эйлера (его погрешность убывает пропорционально лишь первой степени h) является серьезным препятствием для использования его на практике. Из рис. (4) видно, что уже один шаг по касательной к интегральной кривой приводит к значительной величине локальной погрешности ln.
Возникает вопрос: можно ли так подправить расчетную формулу метода, чтобы существенно уменьшить значение ln?
Пусть
y(t) – решение дифференциального уравнения
y¢(t) = f(t, y(t)), (16)
удовлетворяющее условию y(tn)=yn. Далее пусть 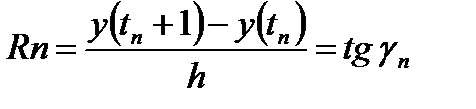 (17) - угловой коэффициент секущей, проходящей через точки (tn, y(tn)) и (tn+1, y(tn+1)) графика функции y(t) (см.рис.7) ясно, что «метод», состоящий в вычислении по формуле
(17) - угловой коэффициент секущей, проходящей через точки (tn, y(tn)) и (tn+1, y(tn+1)) графика функции y(t) (см.рис.7) ясно, что «метод», состоящий в вычислении по формуле
yn+1 = yn+ hrn, (18)
имеет нулевую локальную погрешность.
Для того, чтобы воспользоваться этой формулой нужно лишь «научиться вычислять значения rn». Интегрируя обе части уравнения (16) по t от tn до tn+1 и используя формулу Ньютона – Лейбница
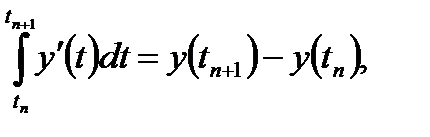
приходим к равенству
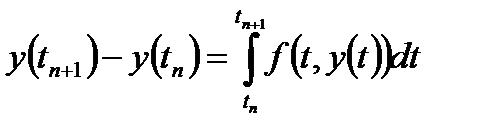 (19)
(19)
Из равенств (17) и (19) следует, что 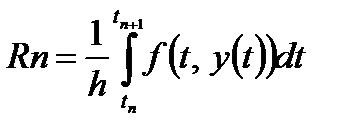 (20)
(20)
Заметим, что применение для приближенного вычисления интеграла, стоящего в правой части выражения (20) формулы левых прямоугольников 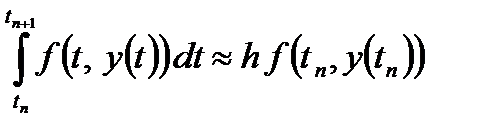 немедленно приводит от формулы (18) к методу Эйлера, /* yn+1 = yn + hf(tn, yn) */ то есть формуле (13)
немедленно приводит от формулы (18) к методу Эйлера, /* yn+1 = yn + hf(tn, yn) */ то есть формуле (13)
Известно, что больший порядок точности имеет формула трапеций:
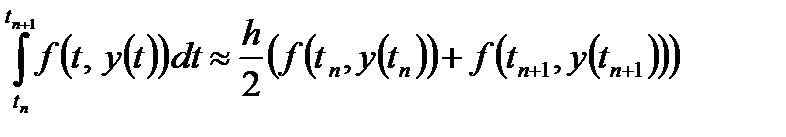 .
.
Непосредственное её применение к вычислению rn приводит к правилу трапеций
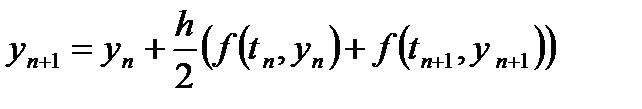 (21)
(21)
Этот метод является методом второго порядка точности, но является неявным, поэтому его реализация связана с необходимостью решения относительно yn+1 нелинейного уравнения (21).
Построим на основе правила трапеций явный метод. Для этого подставим в правую часть формулы (21) значение yn+1, «предсказываемое» методом Эйлера. В результате получается метод
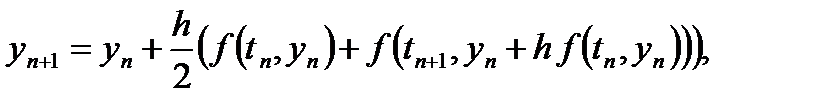 (22)
(22)
который называется методом Эйлера – Коши (или методом Хьюна).
Геометрическая интерпретация этого метода представлена на рис. 8. Вычисления разбивают на 2 этапа. На первом этапе (этапе прогноза) в соответствии с методом Эйлера 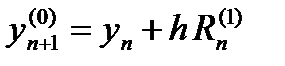
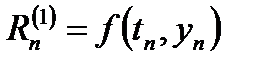 вычисляют грубое приближение к значению y(tn + 1).
вычисляют грубое приближение к значению y(tn + 1).
В точке 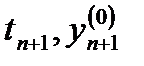 определяют угловой коэффициент
определяют угловой коэффициент 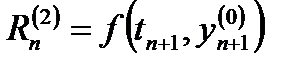 .
.
На втором этапе (этапе коррекции) вычисляют усредненное значение углового коэффициента 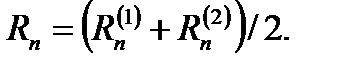
Уточненное значение yn+1 находят по формуле yn+1 = yn + h * Rn, что соответствует шагу по прямой, проходящей через точки (tn, yn) и имеющей угловой коэффициент, равный Rn.
Замечание. Метод Эйлера – Коши относиться к классу методов прогноза и коррекции (иначе говоря, методов типа предиктор – корректор /* topredict - предсказывать; прогнозировать; tocorrect - исправлять, корректировать*/)
Метод (22), который можно рассматривать как модификацию метода Эйлера, имеет второй порядок точности. Ещё одну модификацию второго порядка точности можно получить с помощью формулы (центральных) прямоугольников:
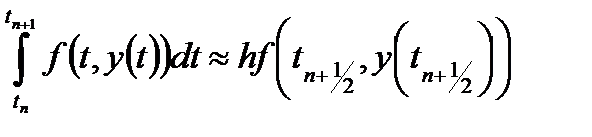
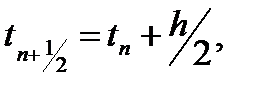
если для приближенного вычисления значения 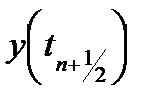 применять метод Эйлера. В результате получим расчетные формулы усовершенствованного метода Эйлера
применять метод Эйлера. В результате получим расчетные формулы усовершенствованного метода Эйлера

(23)
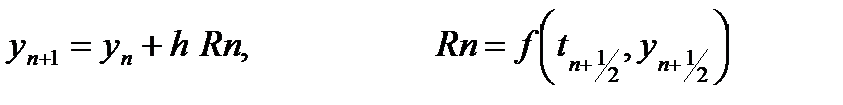
Геометрическая иллюстрация этого метода приведена на рис.9.
Приведем схему алгоритма усовершенствованного метода Эйлера.
| N- количество разбиений отрезка [A, B]
X1, Y1 – значения искомой функции с шагомh
e - заданная точность
|
| xi=xi–1+H
yi=формула Эйлера
|
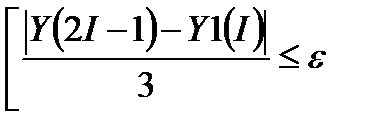
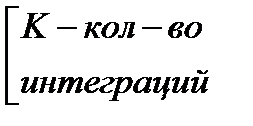
Например,
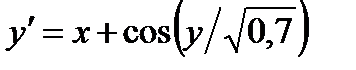
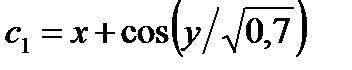
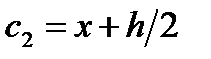
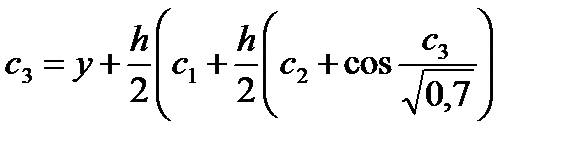
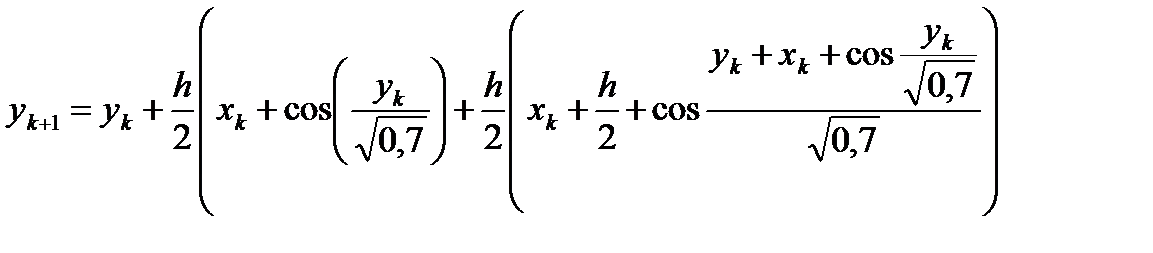
Методы Рунге – Кутты
Наиболее популярными среди классических явных одношаговых методов является методы Рунге – Кутты.
/* Мартин Вильгельм Кутта (1867 - 1944) – немецкий математик. Первые методы этого типа Рунге предложил в 1895г. Позже и независимо в 1901г. Кутта дал общую схему вывода этих методов */
Методы Эйлера, Эйлера – Коши и усовершенствованный метод Эйлера можно рассматривать как простейших представителей этого класса методов.
Дата добавления: 2018-06-27; просмотров: 365; | Поделиться с друзьями:
|

Мы поможем в написании ваших работ!
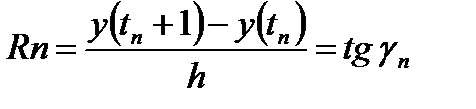 (17) - угловой коэффициент секущей, проходящей через точки (tn, y(tn)) и (tn+1, y(tn+1)) графика функции y(t) (см.рис.7) ясно, что «метод», состоящий в вычислении по формуле
(17) - угловой коэффициент секущей, проходящей через точки (tn, y(tn)) и (tn+1, y(tn+1)) графика функции y(t) (см.рис.7) ясно, что «метод», состоящий в вычислении по формуле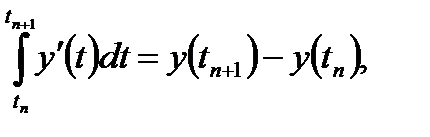
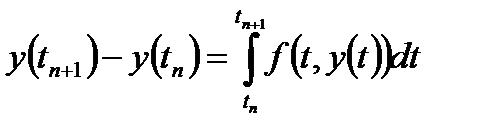 (19)
(19)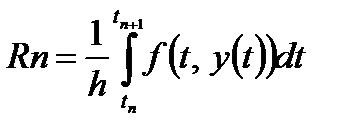 (20)
(20)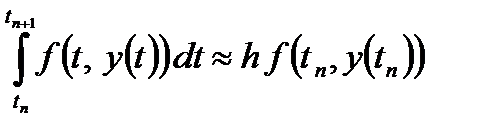 немедленно приводит от формулы (18) к методу Эйлера, /* yn+1 = yn + hf(tn, yn) */ то есть формуле (13)
немедленно приводит от формулы (18) к методу Эйлера, /* yn+1 = yn + hf(tn, yn) */ то есть формуле (13)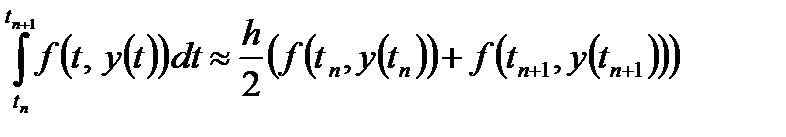 .
.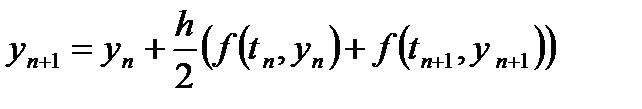 (21)
(21)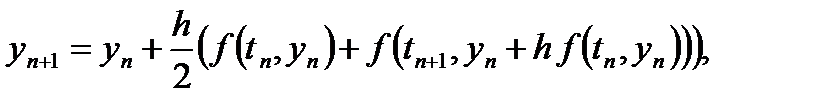 (22)
(22)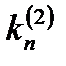
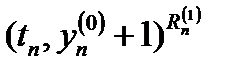
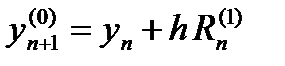
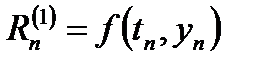 вычисляют грубое приближение к значению y(tn + 1).
вычисляют грубое приближение к значению y(tn + 1).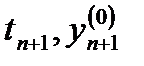 определяют угловой коэффициент
определяют угловой коэффициент 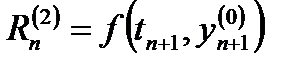 .
.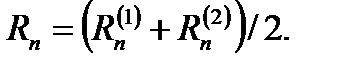
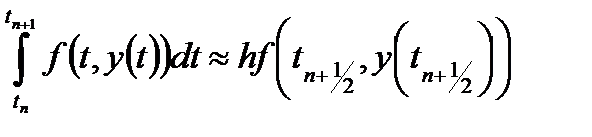
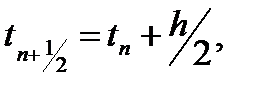
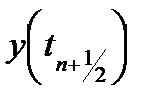 применять метод Эйлера. В результате получим расчетные формулы усовершенствованного метода Эйлера
применять метод Эйлера. В результате получим расчетные формулы усовершенствованного метода Эйлера (23)
(23)