Зведення задачі до хордових діаграм
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ
“КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ ІМ. І. СІКОРСЬКОГО”
Фізико-математичний факультет
Кафедра диференціальних рівнянь
Курсова робота
з дисципліни «Диференціальні рівняння»
«Підрахунок кількості атомів з однією особливою точкою»
Виконав: студент гр. ОМ-61
Лощилін В. О.
Затвердив: Пелюх Г. П.
Київ 2018
ЗМІСТ
1. Введення. 3
1.1 Історія питання. 3
1.2 Результати даної роботи. 5
2 Постановка проблеми. 5
2.1 Означення атома. 5
2.2 Зведення задачі до хордових діаграм. 6
3 Підрахунок кількості класів еквівалентності хордових діаграм з 
вершинами з точністю до симетрій. 10
3.1 Формули для знаходження числа класів еквівалентності хордових діаграм з вершинами з точністю до симетрій. 10
3.2 Доведення рекурентних співвідношень для 
.......... 12
3.3 Доведення рекурентних співвідношень для 
......... 15
3.4 Доведення рекурентних співвідношень для 
......... 17
3.5 Доведення Теореми 3.1.2. 18
4 Алгоритм підрахунку кількості вироджених 2-атомів з одною особливістю степеня і приклади. 19
|
|
|
4.1 Алгоритм. 19
4.2 Приклад для 
........ 20
4.3 Приклад для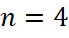 
........ 21
1. Введення
Історія питання
Поняття атома було введено А.Т. Фоменко для якісного вивчення гамільтонових систем (див. [1]). Атом описує біфуркацію торів Ліувілля в прообраз критичного значення функції морсу, визначеної на сімплектичному різноманітті. У разі систем з двома ступенями свободи виникають тривимірні ізоенергетичні різноманіття (при 
). Таким чином 3-атоми (тобто тривимірні атоми (див. [1], [2])) класифікують особливості шарування Ліувілля. В [1], [2] доведено, що тривимірні атоми однозначно, з точністю до гомеоморфізму, кодуються двовимірними атомами.
А.Т. Фоменко була поставлена задача: "Описати 2-атоми, що відповідають функціям з виродженими крититичними точками". В якості першого важливого кроку було вирішено досліджувати атоми з одною виродженою критичною точкою ступеня . Виявляється, що вивчення 2-атомів можна звести до вивчення хордових діаграм (з точністю до симетрії).
В [3], [4] обчислено кількість хордових діаграм з точністю до поворотів (див. [3], Khruzin) і поворотів і симетрій (див. [4], Манойло). У роботах [3] і [4] питання про хордові діаграми, відповідних орієнтуючих атомів не ставилося.
|
|
|
Також є роботи з побудови алгоритмів знаходження на комп'ютері хордових діаграм з точність до поворотів, наприклад в статтях | 5 | і | 6 |. В результаті роботи алгоритмів видаються кодування відповідних хордових діаграм. В.О.Мантуров в статті | 7 | за допомогою мови Mathematica 3.0 перерахував хордові діаграми з вершинами і привів їх для 
.
Для звичайних (не чорно-білих) хордових діаграм їх кількість, знайдена в даній роботі збігається з результатами робіт | 3 |, | 4 | для невеликих розмірностей (до ). Відзначимо, що кількість хордових діаграм росте дуже швидко, наприклад кількість хордових діаграм з точністю до поворотів при 
дорівнює 13176573910, як зазначено в роботі | 5 | Joe Sevada. Асимптотика зростання знайдена A.Khruzin в роботі | 3 | і дорівнює 
для хордових діаграм з точністю до поворотів і 
для хордових діаграм з точністю до поворотів і симетрій. Причини появи таких чисел такі: кількість хордових діаграм з фіксованою нумерацією вершин дорівнює 
, при 
практично всі хордові діаграми не мають симетрій і мають період , а будь-яка хордова діаграма, що має період і не має осей симетрій бере участь у вираженні 
рівно рази з точністю до поворотів і 
рази з точністю до поворотів і симетрій. Аналогічно, кількість чорно-білих діаграм з точністю до поворотів дорівнює 
і з точністю до поворотів і симетрій 
, так як кількість чорно-білих хордових діаграм з фіксованою нумерацією вершин дорівнює 
(беремо першу чорну вершину, їй відповідає одна з 
білих, наступній чорній – одна з 
білих і т.д.). Звідси можна зробити висновок, що частка кількості класів еквівалентності орієнтованих вироджених атомів серед усіх атомів прагне до 0, так як 
і 
при 
.
|
|
|
Для хордових діаграм з фіксованим напрямком обходу і початком відліку можна розглядати орієнтовані поверхні які відповідають їм, що виходять приклейкою неперекручених стрічок замість хорд до границі диска і подальшої заклейки граничних кіл дисками. Таким чином, кожній хордовій діаграмі можна поставити у відповідність число – рід відповідної хордовою діаграмі поверхні. Формула Харера-Загіра дає характеристичну функцію числа хордових діаграм роду 
(див. | 8 |), а також в роботі | 9 | показано, що ці числа розподілені нормально з математичним очікуванням 
і дисперсією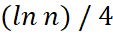 
.
Поняття атома також становить інтерес для теорії вузлів і комбінаторики. Наприклад в теорії інваріантів Васильєва чорно-білі хордові діаграми, що розглядаються в теоремі 3.1.1 відповідають хордовим діаграмам з парними хордами.
|
|
|
Результати даної роботи
У нашій роботі було проведено аналіз 2-атомів з одною критичною точкою. Задача була зведена до дискретної шляхом доведення існування бієкції між класами еквівалентності 2-атомів (з точністю до гомеоморфізма) і безліччю хордових чорно-білих хордових діаграм (з точністю до поворотів і симетрій). Доведення приведено в Затвердженні 2.2.1.
Для отримання кількості хордових діаграм степені (з точністю до поворотів і відображень) в основу були взяті праці [3] і [4], як результат сформульована Теорема 3.1.1. У Теоремі 3.1.1 отримані рекурентні співвідношення, на що Ніконовим І.М. було помічено, що можливе подання даних формул в не рекурентному вигляді, в наслідок чого була отримана Теорема 3.1.2
Також в роботі наведені приклади підрахунку класів еквівалентності вироджених 2-атомів з однією критичною точкою для невеликих .
Постановка проблеми
Означення атома
Для початку введемо поняття виродженого седлового атома з однією вершиною.
Означення 2.1.1 (Вироджений седловий атом з однією вершиною ступеня (2-атом)). Упорядкована пара 
, де P - компактна зв'язкова двовимірна поверхня з краєм, а K - це вкладений в неї граф, у якого одна вершина і ребер (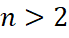 
), називається "виродженим седловим атомом з однією вершиною", якщо:
1) кожна з компонент зв'язності 
гомеоморфна кільцю 
, де I – це напівінтервал, а S – це окружність;
2) кожне кільце можна пофарбувати в один з двох кольорів так, що до кожного ребра графа 
в поверхні 
примикали кільця різних кольорів. Степінь атома визначимо, як число .
При такому означенні легко успадковується поняття "орієнтованості" і "еквівалентності" з класичної теорії поверхонь.
Означення 2.1.2. Орієнтований атом є орієнтованим, якщо орієнтована відповідна поверхня .
Означення 2.1.3 (Еквівалентність двох атомів). Атоми є еквівалентними, якщо існує гомеоморфізм відповідних пар (кольори розмальовки при цьому можна одночасно змінювати на протилежні).
Тепер ми можемо розглядати класи еквівалентності 2-атомів і виникає природне запитання: скільки всього класів еквівалентності? Для вирішення даного завдання ми розіб'ємо його, природним чином, на завдання підрахунку окремо кількості класів еквівалентності орієнтованих 2-атомів і неорієнтованих.
Для повноцінного зведення задачі до комбінаторної дуже зручним виявилося поняття хордової діаграми і чорно-білої хордової діаграми.
Зведення задачі до хордових діаграм
Означення 2.2.1 (Хордова діаграма з вершинами). Хордовою діаграмою з вершинами називається множина з точок в вершинах правильного багатокутника і окружності, якої вони належать, занумерованих за годинниковою стрілкою натуральними числами від 
до , з проведеними між ними відрізками, званими хордами і розподіляючими точки на пари. Крапку з номером 1 називають початком відліку. Причому багатокутник заданий на стандартній площині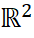 
, його центр збігається з точкою 
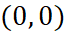і вершина з номером має координату 
.
Хордові діаграми можна ототожнювати з 2-атомами з однією особливістю, в той час, як для опису орієнтованих 2-атомів найкращим чином підходить поняття "чорно-білої хордовою діаграми":
Означення 2.2.2 (Чорно-біла хордова діаграма з вершинами). Чорно-білої хордовою діаграмою з вершинами називається хордова діаграма з розфарбованими по черзі в чорний і білі кольори вершинами, в якій кожна хорда з'єднує вершини тільки різного кольору.
Зауваження 1. Розфарбовування не фіксоване, тобто його можна одночасно змінювати на протилежне у всіх вершин. Нам буде важливо тільки те, що хорди з'єднують вершини з різних класів. Наступні означення вводяться аналогічно для чорно-білих діаграм.
Зауважимо також, що так як 2-атоми ми розглядаємо з точністю до гомеоморфізму, то і на множині всіх хордових діаграм потрібно ввести деякі симетрії: поворот на кут 
відносно центру кола і відображення щодо основного діаметра.
Означення 2.2.3 (Еквівалентність двох 2-атомів). Дві хордові діаграми називаються еквівалентними з точністю до поворотів і відображень, якщо існує поворот або віддзеркалення щодо осі, що проходить через початок координат,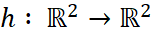 
(або їх композиція), яка переводить першу хордову діаграму у другу (без урахування нумерації вершин).
Раціонально буде розглядати не всі хордові діаграми, а класи еквівалентності відносно перерахованих вище симетрій.
Тепер покажемо схожість двох множин: множини класів еквівалентності вироджених сідлових атомів з однією вершиною степені і безлічі класів еквівалентності хордових діаграм з вершинами (класи еквівалентності відносно введених на множинах симетрій).
Твердження 2.2.1. Існує природна біекція між безліччю класів еквівалентності вироджених сідлових атомів з одною виродженою точкою і безліч класів еквівалентності хордових діаграм з вершинами.
Доведення. Побудуємо відображення з класу еквівалентних атомів в клас еквівалентних, з точністю до повороту і симетрій, хордових діаграм і покажемо, що воно є біекцією. Розглянемо гомеоморфні околиці критичної точки атома ступеня диск в стандартній площині 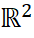з центром на початку координат і радіусом 1. На кордоні диска задана послідовність точок перетину ребер графа і диска, перенумеруємо точки за годинниковою стрілкою числами від до , вибравши будь-яку з них в якості першої. Відомо, які пари точок з'єднані ребром в графі , а значить і в послідовності нумерованих вершин. Побудуємо відповідному атому хордову діаграму з точністю до поворотів і відображень. На колі радіуса в стандартній площині розташуємо точки в вершинах правильного багатокутника, занумеруємо їх за годинниковою стрілкою так, що вершина з номером має координату і побудуємо хорди між вершинами з тими номерами, які з'єднані ребром графа в послідовності перенумерованих вершин на диску. Покажемо проведені перетворення на прикладі:
(a) (b) (c)
Мал. 1: Приклад побудови відображення: (a) приклад виродженого седлового атома ступеня 6; (b) відповідність між полу ребрами графа виродженого атома і вершинами хордової діаграми; (c) відповідна атому хордова діаграма.
Покажемо коректність побудованого відображення, для цього потрібно показати, що еквівалентні атоми перейдуть в еквівалентні з точністю до поворотів і симетрій хордові діаграми.
Гомеоморфізм атомів можна обмежити на околицю критичної точки, тому, якщо розглянути для двох еквівалентних атомів відповідні їм диски та побудовані за ним хордові діаграми, то хордові діаграми можуть відрізнятися одна від одної поворотом і відображенням (з огляду на неоднозначність вибору точки початку відліку і напрямки обходу на граничних околах дисків).
Доведемо бієктивніть побудованого відображення. Для будь-якої заданої хордовою діаграми побудуємо єдиний з точністю до гомеоморфізму відповідний їй атом. Нехай є хордова діаграма з вершинами, "перекидаємо ребра в зовнішню сторону кола", проводимо відрізки, що з'єднують вершини з початком координат. На цьому етапі отримуємо граф і околицю критичної точки атома, до якої згодом будемо приклеювати стрічки. Тимчасово розфарбуємо вершини хордовою діаграми в чорний і білий кольори в шаховому порядку. З кожною частиною ребра графа K, що з'єднує вершини хордової діаграми і знаходиться поза окружності проведемо наступну операцію: якщо вона з'єднує вершини різних кольорів, то приклеюємо до диска на даних місцях неперекручену стрічку з намальованою на ній частиною ребра графа , інакше - перекручену. Далі фарбуємо сектори диска в шаховому порядку в чорний і білий кольори і продовжуємо розмальовку на компоненти зв'язності різноманіття . Так як при побудові атома ми можемо забути про нумерацію вершин диска, в якому розташовуються кінців полу ребер, то атом виникає єдиний з точністю до гомеоморфізму. Проілюструємо сказане на прикладі:
Так встановлена взаємооднозначна відповідність між класами еквівалентності атомів і хордових діаграм. ▲
(a) (b) (c) (d)
Мал. 2: Приклад побудови відображення: (a) хордова діаграма; (b) "прокидаємо хорди"; (c) побудова графа ; (d) відповідний атом.
3 Підрахунок кількості класів еквівалентності хордових діаграм з 
вершинами з точністю до симетрій
3.1 Формули для знаходження числа класів еквівалентності хордових діаграм з вершинами з точністю до симетрій
Будемо вважати, що у нас є хордова діаграма з вершинами, тоді
Означення 3.1.1 (Період хордової діаграми). Періодом (відповідно найменшим позитивним) хордової діаграми будемо називати кількість (відповідно мінімальне позитивне) вершин, на яке потрібно її повернути так, щоб всі хорди вихідної діаграми збіглися з хордами поверненою. Хордові діаграми з найменшим періодом 
називають "діаграмою типу 
".
Означення 3.1.2 (Відстань від вершини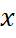 
до вершини 
). Мінімальна невід'ємна кількість вершин, на яку потрібно повернути хордову діаграму так, щоб вершина 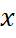перейшла в називається відстанню від 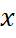до .
Нехай:
– це кількість хордових діаграм типу з 
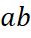вершинами з точністю до поворотів;
– це кількість хордових діаграм з вершинами з точністю до поворотів і мають вісь симетрії;
– це кількість хордових діаграм з вершинами з точністю до поворотів і відображень.
Теорема 3.1.1. Числа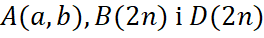 
однозначно визначаються наступними рекурентними співвідношеннями:
.
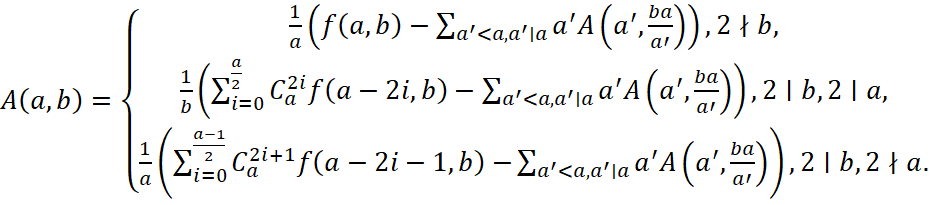
, де 
,
, причому 
.
Також сформулюємо теорему, в якій числа виражаються нерекурентними формулами:
Теорема 3.1.2. Числа 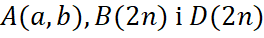однозначно визначаються наступними явними формулами:
.
, де ,
– функція Мебіуса
, причому .
Відзначимо, що явні формули для чисел мають переваги, в разі, якщо є необхідність порахувати кількість 2-атомів з досить великим найменшим періодом, зробивши найменшу кількість операцій. Але рекурентні формули залишаються в плюсі, при необхідності отримати повну картину, за рахунок відсутності в записі формули Мебіуса, яка займає занадто багато роботи на комп'ютерах.
Докази формул будуть наведені нижче.
3.2 Доведення рекурентних співвідношень для 
У хордовій діаграмі типу виберемо перші поспіль вершин. По тому, з якими точками вони з'єднані, можна відновити всю хордову діаграму. Таким чином, всі точки розбиті на 
періоди, в кожному з яких точок, які будемо нумерувати від до . Період, в якому лежить початок відліку, занумеруємо числом . З рештою періодами можна порівняти натуральні числа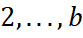 
за годинниковою стрілкою. Візьмемо точку з номером 
в першому періоді, і нехай вона з'єднана з точкою 
. Порівняємо точку i пару чисел 
, де 
– номер точки в своєму періоді і 
– номер періоду, в якому вона знаходиться. Зауважимо, що таким кодуванням ми просто показали, що відстань між точкою з номером в будь-якому періоді до її пари дорівнює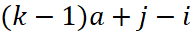 
. Таким чином, кожній хордовій діаграмі типу ми зіставили послідовність з пар чисел. Надалі іноді ми будемо позначати пару однією літерою, а не двома. Так, запис 
може позначати те, що пара 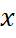збігається з парою .
Лема 3.2.1. Нехай дана хордова діаграма типу . Якщо при повороті на вершин послідовності, відповідальні вихідній і отриманій хордовим діаграмам, збігаються, то кратно .
Доведення. Так як найменший позитивний період хордової діаграми дорівнює , без обмеження спільності будемо вважати, що поворот відбувається на 
вершин. Нехай при повороті на вершин одержується хордова діаграма, якій зіставляється та ж послідовність з пар, що і вихідній діаграмі. Позначимо підпослідовність з пар, що відповідають точкам періоду з номерами 
, через 
.
Так як зрушена на одиниць послідовність починається також з підпослідовності , то результатна послідовність починається з двох, що стоять поспіль підпослідовностей . Повертаємося до зрушеної послідовності, вона починається з двох, що стоять поспіль послідовностей, значить, вихідна послідовність починається з трьох підпослідовностей і т.д. На -му кроці отримуємо, що початкова послідовність починається з , що стоять поспіль підпослідовностей . Це міркування ми можемо проводити необмежену кількість раівз, навіть коли 
, що означає, що – це період хордової діаграми, але 
, a – це найменший період хордової діаграми, значить, 
, звідки випливає твердження леми. ▲
Тепер доведемо наступну формулу:
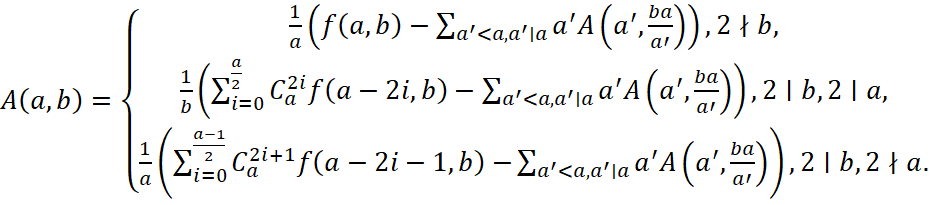
Розглянемо випадок, коли b - непарне.
Візьмемо точку з номером 
і подивимося, яка пара може ставитися їй у відповідність. Номер може бути будь-яким в 
крім , так як інакше вершині з номером в періоді з номером ставиться в відповідність вершина з номером в періоді з номером 
. З чого можна зробити висновок, що 
, але b непарне. Таким чином, для першої вершини номер може приймати 
значень, а – будь-яке із 
значень. Тобто, варіантів пар 
. Відзначимо, що точці з номером однозначно зіставляється пара 
. Для наступної вершини аналогічно кількість можливих пар 
і т.д. Так як кількість кроків дорівнює 
, Отримуємо 
хордових діаграм з (необов'язково найменшим) періодом . Зауважимо, що ми порахували також і "зайві" хордові діаграми – це ті, у яких мінімальний період пошукової роботи не , a a 
, де 
. Більш того, якщо ототожнити хордові діаграми, що відрізняються поворотом, то кожну з них ми порахували рівно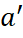 
раз в силу леми 1. Після вирахування "зайвих" хордових діаграм залишається 
– це діаграми, у яких мінімальний період дорівнює . Але знову ж таки, якщо ототожнювати хордові діаграми, що відрізняються поворотом, в силу леми 1 кожну з них ми порахували раз, значить, потрібно на розділити. Отримуємо необхідну відповідь.
Розглянемо випадок, коли – парне. Відмінність від випадку непарного в тому, що тепер точці з номером може бути порівняна протилежна вершина в багатокутнику, тобто пара 
( 
може дорівнювати ). Назвемо такі точки особливими. Тоді з'являється залежність ще й від парності , так як, якщо парне, то особливих точок в періоді парне число, а при непарному – непарне.
Нехай в періоді 
особливих точок, тоді кількість діаграм типу дорівнює 
. Тут 
відповідає за те, які саме точки в періоді особливі, a 
вважається аналогічно першому випадку після виключення особливих точок. Таким чином, нами доведена справедливість формули для обчислення .
3.3 Доведення рекурентних співвідношень для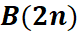 
До сих пір ми розглядали хордові діаграми тільки з точністю до поворотів, тепер додамо осьові симетрії. На відміну від , для підрахунок проводитиметься відразу для всієї діаграми без урахування мінімального періоду.
Нехай хордова діаграма типу симетрична відносно будь-якої осі. Вісь симетрії (або просто вісь) може проходити або через протилежні вершини багатокутника (тоді вони з'єднані хордою), або між вершинами (отже, будь-які дві осі виходять одна з одної поворотом на напівціле число точок). Вивчимо, який вид може мати період хордової діаграми в кожному з цих випадків розташування осі.
Надалі нам знадобиться
Лемма 3.3.1. Якщо a – це мінімальний позитивний період хордової діаграми, то всі осі симетрії виходять одна з одної поворотами на цілу або напівцілу кількість точок, кратне 
.
Доведення. Нехай хордова діаграма симетрична щодо деякої осі 
, а також щодо осі, що вийшла з за допомогою повороту за годинниковою стрілкою на точок. Композиція симетрій щодо двох зазначених осей – це поворот на 
точок. Вона переводить хордову діаграму в себе, тобто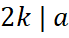 
. З умови про те, що мінімальний період слідує лема. ▲
Лема 3.3.2. Для виконуються наступні співвідношення:
, де .
Доведення. Випадок 1: Нехай у хордової діаграми існує вісь симетрії, що проходить між вершинами. 
– це кількість хордових діаграм (деякі, можливо, підраховані кілька разів, що буде пояснено пізніше), у яких існує вісь симетрії такого типу. За аналогією з підрахунком виберемо 
вершин з одної сторони від обраної осі, яким будуть відповідати вершини, симетричні щодо даної осі. Точкам 
, які залишилися, будуть відповідати 
варіантів зіставлення точок. Причому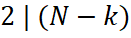 
. Таким чином, вираз для такий:
.
Випадок 2: Нехай у хордової діаграми існує вісь симетрії, що проходить через протилежні вершини багатокутника. 
– це кількість хордових діаграм (аналогічно першому випадку деякі, можливо, підраховані кілька разів), у яких існує вісь симетрії такого типу. Підрахунок аналогічний першому випадку, за винятком того, що в початковий момент дві вершини вже "зайняті" (через них вже проходить хорда).
Таким чином, вираз для такий:
.
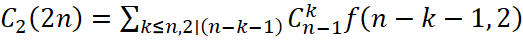Зауважимо, що 
.
Твердження 3.3.1. Будь-яка симетрична діаграма бере участь рівно два рази в підрахунку 
.
Доведення. Залежно від парності довжини мінімального періоду і їх кількості ( і відповідно) можна виділити три види розташування осей симетрії.
Випадок 1: Якщо непарне (а значить парне). У такому випадку всі осі симетрії обов'язково проходять між вершинами, причому один з кінців розташовується в середині періоду, а другий проходить між періодами. Як відомо, все осі симетрії виходять при повороті діаграми на точок. В цьому випадку при такому повороті виходить діаграма, що збігається з вихідною при повороті на π. Тобто такі діаграми підраховані рівно два рази в по одному з кожного з кінців осі.
Випадок 2: Якщо парне, а непарне. В такому випадку у діаграми рівно два класи осей симетрії, одному з яких належать осі, що проходять через протилежні точки, які є центрами періоду, а значить вони підраховані в , а другому класу належать осі, що проходять між періодами, а значить вони включені в підрахунок .
Випадок 3: Якщо і парні. В такому випадку у діаграми також рівно два типи осей симетрії, осі одного з яких проходять між періодами, а другого посередині двох протилежних періодів. ▲
Таким чином твердження вірне і кількість симетричних діаграм дорівнює 
. А значить доведена і лема. ▲
3.4 Доведення рекурентних співвідношень для 
У лемах 2 і 4 знайдені співвідношення для 
. Очевидно, що безліч всіх хордових діаграм з вершинами можна розбити на непересічні підмножини:
X – хордові діаграми з точністю до поворотів, у яких немає жодної осі симетрії,
Y – хордові діаграми з точністю до поворотів, у яких є вісь симетрії,
де 
- кількість елементів у відповідних множинах.
Твердження 3.4.1. У виразі 
кожна діаграма порахована рівно 2 рази.
Доведення. Зауважимо, що якщо хордова діаграма не має осі симетрії (належить іножеству X), тоді вона бере участь в підрахунку 
рівно два рази, і жодного разу в . Якщо ж хордова діаграма має вісь симетрії (належить множині Y), вона бере участь по одному разу в і . ▲
Слідство. За попереднім твердженням
.
Теорема 3.1.1 доведена.
Доведення Теореми 3.1.2
Для доведення теореми будемо вважати, що Теорема 3.1.1 вже відома, і спробуємо просто перетворити формули для вираження чисел .
Скористаємося наступною теоремою з курсу Теорії Чисел:
Теорема 3.5.1. (Формула звернення Мебіуса) Для арифметичних функцій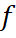 
і
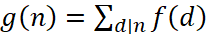
тоді і тільки тоді, коли
Запишемо і перетворимо в загальному вигляді вирази для :
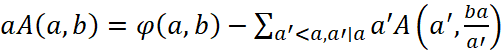
Пам'ятаємо, що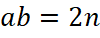 
і фіксуємо
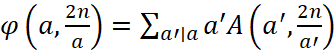
Звідси по Формулі Звернення Мебіуса
або 
Таким чином наведені явні вирази для функції через яку виражається загальна кількість класів еквівалентності хордових діаграм, а відповідно і 2-атомів з точністю до гомеоморфізму.
4 Алгоритм підрахунку кількості вироджених 2-атомів з одною особливістю степеня і приклади
Алгоритм
Нагадаємо, що визначення основних функцій, які ми ввели раніше:
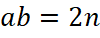– це кількість хордових діаграм з точністю до поворотів і мінімальним періодом довжини і вершинами;
– це кількість хордових діаграм з вершинами з точністю до поворотів і мають вісь симетрії;
– це кількість хордових діаграм з вершинами з точністю до поворотів і відображень (кількості вироджених атомів ступеня , а також кількість орієнтованих 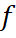-атомів з одною граничною чорною окружністю).
Поставимо мету порахувати число . За Теоремою 3.1.1:
.
Для підрахунку загальної кількості необхідно порахувати для всіх 
числа 
.
4.2 Приклад для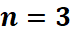 
Знайдемо їх значення для :
, (єдина діаграма, що має період 1)
, (єдина діаграма, що має період 2)
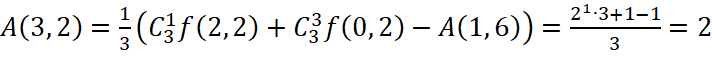, (дві діаграми, що мають період 3)
ng w:val="UK"/></w:rPr><m:t>=1</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 
, (єдина діаграма, що немає періоду меншого за 6)
,
.
Нижче наведені відповідні хордові діаграми і 2-атоми (див. Рис. 3 і Рис. 4 відповідно)
Мал. 3: Хордові діаграми з точністю до поворотів і симетрій для .
Мал. 4: Атоми ступеня 6, відповідні даним хордових діаграмам.
В даному випадку всі діаграми мають вісь симетрії, що вводить в деякі сумніви, але в наступному прикладі приведена більш повна картина.
4.3 Приклад для 
Аналогічним чином обчислимо всі необхідні значення:
,
,
,
,
,
.
В даному випадку чітко видно атом, який не має осі симетрії (див. Рис. 5: другий ряд, п'ятий стовпець).
Мал. 5: Хордові діаграми з точністю до поворотів і симетрій для .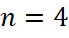
Мал. 6: Атоми ступеня 8, відповідні даним хордових діаграмам.
Дата добавления: 2018-06-27; просмотров: 616; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!