Применение функций в экономике. Интерполирование функций

Основные элементарные функции

В таблице приводятся наиболее важные свойства и графики основных элементарных функций.

Степенная функция

№ п/п	Обозначение функции	Область определения Х	Область значений Y	Четность, нечетность	Монотонность	Периодичность
1	у=хⁿ п Î N	(–µ, +µ)	(–µ, +µ), если п – нечетно; [0; +µ), если п – четно	нечетная, если п – нечетно; четная, если п – четно	возрастает на (–µ, +µ), если n – нечетно; убывает на (–µ, 0], возрастает на (0, +µ), если п – четно	непериодическая

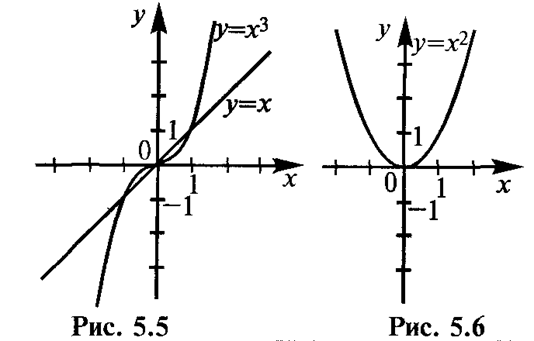
№ п/п	Обозначение функции	Область определения Х	Область значений Y	Четность, нечетность	Монотонность	Периодичность
2	у=х" п Î N	(–µ,0) U U (0, +µ)	(–µ,0)U U (0, +µ), если п – нечетно; [0; +µ), если п – четно	нечетная, если п – нечетно; четная, если n – четно	убывает на (–µ, 0) и на (0, +µ), если п – нечетно; возрастает на (–µ; 0) и убывает на (0, +µ), если п – четно	непериодическая

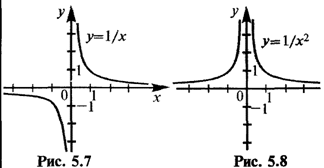
№ п/п	Обозначение функции	Область определения Х	Область значений Y	Четность, нечетность	Монотонность	Периодичность
3	у=Ö х nÎ N п >1	(–µ, +µ) если n – нечетно; [0; +µ), если п – четно	(–µ, +µ), если п – нечетно; [0; +µ), если п – четно	нечетная, если п – нечетно; общего вида, если п – четно	возрастает на (–µ; +µ), если п – нечетно; возрастает на [0; +µ), если п – четно	непериодическая

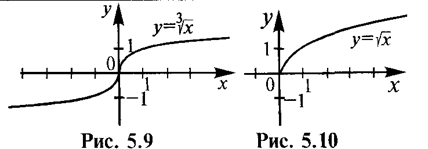
Показательная функция

№ п/п	Обозначение функции	Область определения Х	Область значений Y	Четность, нечетность	Монотонность	Периодичность
4	у = a^x (а>0, а¹1)	(–µ, +µ)	(0; +µ)	общего вида	возрастает на (–µ; +µ), если а > 1; убывает на (–µ; +µ), если 0 < а ^< 1	непериодическая

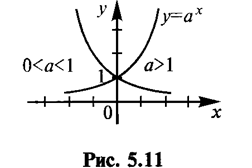
Логарифмическая Функция

№ п/п	Обозначение функции	Область определения Х	Область значений Y	Четность, нечетность	Монотонность	Периодичность
5	у= log_a x (а > 0, a ¹ 1	(0; +µ)	(–µ, +µ)	общего вида	возрастает на (0; +оо), если о > 1; убывает на (0; +µ), если 0 < а < 1	непериодическая

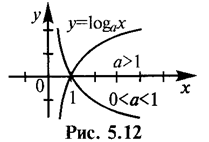
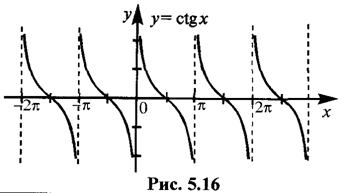
Тригонометрические функции

№ п/п	Обозначение функции	Область определения Х	Область значений Y	Четность, нечетность	Монотонность	Периодичность
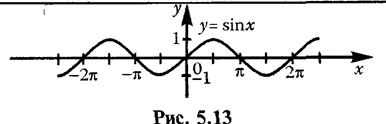
6	у = sin х	(–µ, +µ)	[-1; 1]	нечетная	возрастает на [-p/2+2pn, p/2+2pn]; убывает на [p/2+2pn, Зp/2+2pn], п Î Z	Период T= 2л

№ п/п

Обозначение функции

Область определения Х

Область значений Y

Четность, нечетность

Монотонность

Периодичность

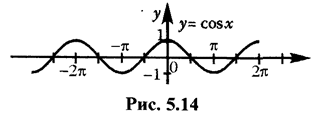
№ п/п

Обозначение функции

Область определения Х

Область значений Y

Четность, нечетность

Монотонность

Периодичность

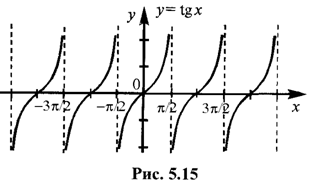
№ п/п

Обозначение функции

Область определения Х

Область значений Y

Четность, нечетность

Монотонность

Периодичность

5. Обратные тригонометрические функции

у = arcsin х, у = arccos х, у = arctg х, у = arcctg x

4. Периодичность. Функция у = f (х) называется периодической с периодом Т ¹ 0, если для любых х из области определения функции f(x+T)=f(x).

Например, функция у = sin х имеет период Т = 2p, так как для любых х sin (х +2л) = sin х.

Элементарные функции. Классификация функций. Преобразование графиков

Функция называется явной, если она задана формулой, в которой правая часть не содержит зависимой переменной; например, функция у = х² + 5х +1.

Функция у аргумента х называется неявной, если она задана уравнением F(х, у) = 0, не разрешенным относительно зависимой переменной. Например, функция у (у > 0), заданная уравнением х³ + у² - х = 0. (Заметим, что последнее уравнение задает две функции

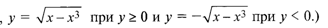
Обратная функция. Пусть у = f (х) есть функция от независимой переменной х, определенной на множестве Х с областью значений Y. Поставим в соответствие каждому у Î Y единственное значение х Î X, при котором f(х) = у. Тогда полученная функция х = j (у), определенная на множестве Г с областью значений X, называется обратной.

Так как традиционно независимую переменную обозначают через х, а функцию через у, то функция, обратная к функции у =f(x), примет вид у = j (х). Обратную функцию у = j(х) обозначают также в виде у = f^–1 (х) (аналогично с обозначением обратной величины).

Например, для функции у = a^х обратной будет функция х = log_a у или (в обычных обозначениях зависимой и независимой переменных) у= log_ax.

Можно доказать, что для любой строго монотонной функции у = j(х) существует обратная функция.

Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (на рис. 5.17 показаны графики взаимно обратных функций у =a^x и у = log_a х при a > 1).

Сложная функция. Пусть функция у =f(u) есть функция от переменной и, определенной на множестве U с областью значений Y, а переменная и в свою очередь является функцией и = j(х) от переменной х, определенной на множестве Х с областью значений U. Тогда заданная на множестве Х функция y = f[j(x)] называется сложной функцией (или композицией функций, суперпозицией функций, функцией от функции).

Например, у = lg sin х – сложная функция, так как ее можно представить в виде у = lg и, где и = sin х.

Понятие элементарной функции. Из основных функций новые функции могут быть получены двумя способами при помощи: а) алгебраических действий; б) операций образования сложной функции.

Определение. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называютсяэлементарными.

Например, функция

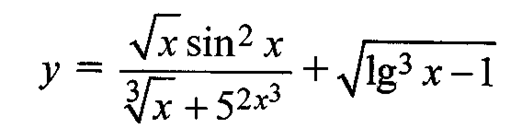
является элементарной, так как здесь число операций сложения, вычитания, умножения, деления и образования сложной функции 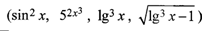конечно.

Примерами неэлементарных функций являются функция у = [х] – целая часть х (см. рис. 6.9), функция Дирихле (с. 127).

Классификация функций. Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).

Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий. К числу алгебраических функций относятся:

• целая рациональная функция (многочлен или полином):

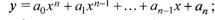
• дробно-рациональная функция – отношение двух многочленов;

• иррациональная функция (если в составе операций над аргументом имеется извлечение корня).

Всякая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические.

Преобразование графиков. В разделе III «Дифференциальное исчисление» будет показано, как проводить исследование функций и построение их графиков с помощью производной. Вместе с тем актуальными остаются приемы построения графиков функций с помощью преобразования графиков основных элементарных функций.

Пусть задан график функции у =f(x).

Тогда справедливы следующие утверждения.

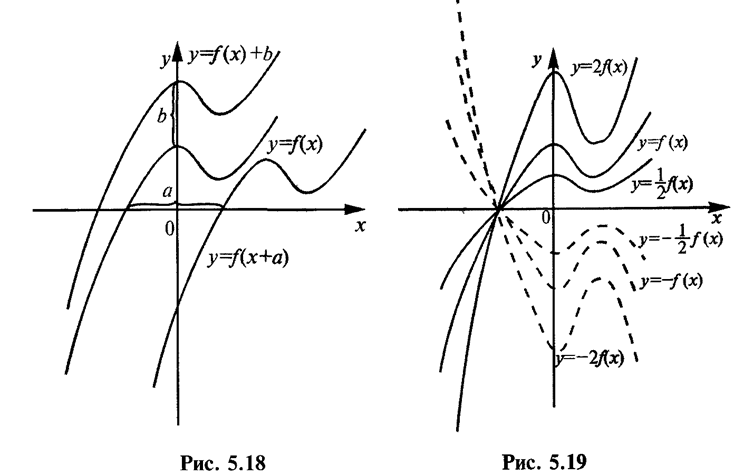
1. График функции у =f(x + а) есть график у = f(х), сдвинутый (при а > 0 влево, при а < 0 вправо) на |a| единиц параллельно оси Ох (рис. 5.18).

2. График функции у =f(x) + b есть график у =f(x), сдвинутый (при b > 0 вверх, при b < 0 – вниз) на |b| единиц параллельно оси Оу (см. рис. 5.18).

3. График функции у = mf(x) (т¹ 0) есть график у =f(x), растянутый (при т>1) в т раз или сжатый (при 0 < т < 1) вдоль оси Оу (см. рис. 5.19). При т < 0 график функции у = mf(x) есть зеркальное отображение графика у = –тf(х) от оси Ох.

4. График функции у =f(kx) (k ¹ 0) есть график у =f(x), сжатый (при k>1) в k раз или растянутый (при 0 < k < 1) вдоль оси Ох (см. рис. 5.20). При -оо < k < 0 график функции у =f(kx) есть зеркальное отображение графика у =f(–kx) от оси Оу.

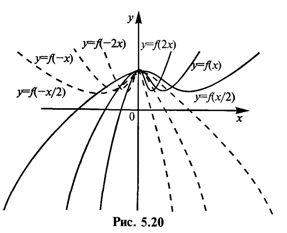
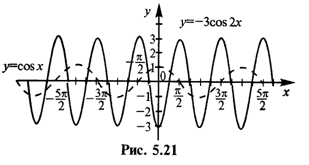
Пример 5.3. Построить график функции у = –3cos 2х.

Решение. Строим график функции у = –3cos 2х следующим образом (рис. 5.21).

1. Строим график у = cos х.

2. у = cos x -> сжатие графика в 2 раза вдоль оси Ох -> у = = cos 2х.

3. у = cos 2x -> зеркальное отражение графика отоси Ох -> у = –cos 2х.

4. у = -cos 2x-> растяжение графика в 3 раза вдоль осиОу -> у = –3cos 2х.

Применение функций в экономике. Интерполирование функций

Остановимся еще на одном важном аспекте использования функций в экономике –применении таблиц функций, которые позволяют сделать возможными различные расчеты, исключить или упростить громоздкие вычисления.

При вычислениях с помощью таблиц мы часто сталкиваемся с ситуацией, когда аргумент функции задан с большей точностью, чем позволяет таблица. В этом случае мы должны прибегнуть к интерполированию (интерполяции) – приближенному нахождению неизвестных значений функций по известным ее значениям в заданных точках.

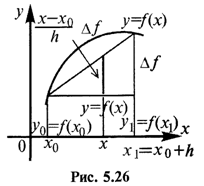
Наиболее простым является линейное интерполирование, при котором допускается, что приращение функции пропорционально приращению аргумента. Если заданное значение х лежит между приведенными в таблице значениями x₀ и x₁ = x₀ + h, которым соответствуют значения функции 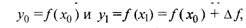считают, что (рис. 5.26)

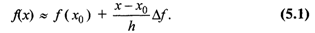
Величины 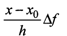называются интерполяционными поправками. Эти величины вычисляются с помощью таблицы или приводятся в дополнении к таблице.

Если по заданным значениям функции необходимо найти приближенное значение аргумента, то необходимо произвести обратное интерполирование.

Пример 5.4. Функция у =f(х) задана таблицей:

х	2	2,04	2,08
у	2,42	2,88	3,38

а) Используя линейное интерполирование, найти f(2,008).

б) Чему равен х, если f(x) =3,1?

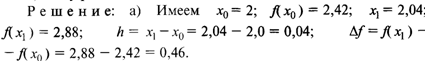
Теперь по интерполяционной формуле (5.1) получим

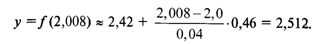
б) Обратное интерполирование можно провести по той же формуле, в которой поменять местами переменные х и у.

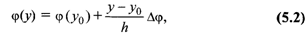
где х = j(у) – неизвестное значение обратной функции.

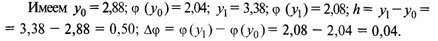
Теперь по интерполяционной формуле (5.2) получим

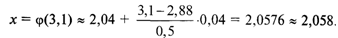
В ряде случаев точность нахождения неизвестных значений с помощью линейного интерполирования оказывается недостаточной и используются другие методы интерполирования, например квадратичное интерполирование.

Решение задач

Пример 5.5. Найти область определения функций

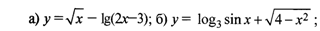
Р е ш е н и е.

а) Область определения функции -Y найдем из системы неравенств

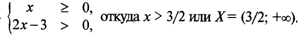
б) Имеем систему

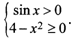
Решая первое неравенство, получим 2pn < х < п+2pп; решая второе, найдем х² < 4, откуда |x| £ 2 и –2 £ х £ 2.С помощью числовой оси (рис. 5.27) находим решение системы неравенств: 0 < х £ 2, т.е. область определения функции Х= (0; 2].

Дата добавления: 2018-06-01; просмотров: 1242; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!