По дисциплине «Математический анализ 2»
Экзаменационные вопросы по дисциплине «Математический анализ»
2 семестр
1. Дифференциальные уравнения высших порядков (основные понятия). Задача Коши.
2. Дифференциальные уравнения высших порядков, допускающие понижение порядка.
3. Линейные однородные дифференциальные уравнения высших порядков. Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами.
4. Линейные неоднородные дифференциальные уравнения высших порядков. Метод Лагранжа.
5. Линейные неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами, метод подбора частного решения.
6. Системы дифференциальных уравнений, основные понятия, задача Коши.
7. Скалярное поле. Характеристики скалярных полей: линии и поверхности уровня, производная по направлению, градиент.
8. Криволинейный интеграл первого рода, его геометрический и физический смысл, свойства.
9. Вычисление криволинейного интеграла первого рода.
10. Поверхностный интеграл первого рода, его геометрический и физический смысл, свойства.
11. Вычисление поверхностного интеграла первого рода.
12. Векторное поле. Характеристики векторных полей: векторные линии, векторные трубки, ротор, дивергенция.
13. Криволинейный интеграл второго рода, его физический смысл, свойства.
14. Вычисление криволинейного интеграла второго рода.
|
|
|
15. Циркуляция векторного поля. Формула Грина. Независимость криволинейного интеграла от выбора пути интегрирования.
16. Поверхностный интеграл второго рода, его физический смысл, свойства.
17. Вычисление поверхностного интеграла второго рода.
18. Дивергенция векторного поля. Теорема Остроградского – Гаусса. Ротор векторного поля. Теорема Стокса.
19. Оператор Гамильтона. Дифференциальные операции первого и второго порядков.
20. Специальные виды векторных полей.
21. Комплексные числа. Арифметические действия над комплексными числами в алгебраической форме.
22. Модуль и аргумент комплексного числа. Тригонометрическая и показательная формы комплексного числа. Арифметические действия над комплексными числами в тригонометрической и показательной формах.
23. Понятие функции комплексной переменной. Предел функции комплексной переменной.
24. Производная функции комплексной переменной. Аналитичность. Свойства аналитических функций.
25. Преобразование Лапласа. Оригинал. Изображение. Таблица оригиналов.
26. Свойства преобразования Лапласа.
27. Восстановление оригинала по изображению.
Задачи для подготовки к экзамену
1. Найти общее решение (общий интеграл) дифференциального уравнения: а) 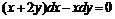 , б)
, б) 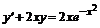 , в)
, в) 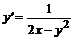 , г)
, г) 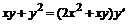 , д)
, д) 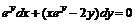 , е)
, е) 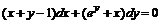 , ж)
, ж) 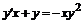 , з)
, з) 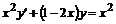 .
.
|
|
|
2. Найти частное решение (частный интеграл): а) 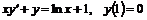 ; б)
; б) 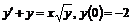 ; в)
; в) 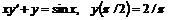 ; г)
; г) 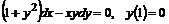 .
.
3. Найти общее решение (общий интеграл) дифференциального уравнения: а) 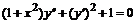 , б)
, б) 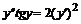 , в)
, в) 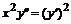 , г)
, г) 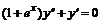 , д)
, д) 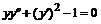 , е)
, е) 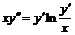 .
.
4. Найти общее решение дифференциального уравнения: а) 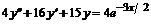 , б)
, б) 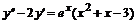 , в)
, в) 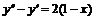 , г)
, г) 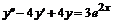 , д)
, д) 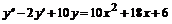 , е)
, е) 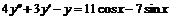 .
.
5. Найти решение задачи Коши: а) 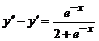 ,
, 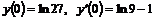 , б)
, б) 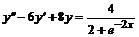 ,
, 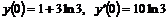 .
.
6. . Решить систему дифференциальных уравнений: а) 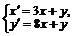 б)
б) 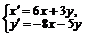 в)
в) 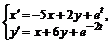 г)
г) 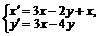
7. Вычислить  , где L- дуга окружности
, где L- дуга окружности 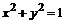 от точки А(-1, 0) до точки В(0, -1).
от точки А(-1, 0) до точки В(0, -1).
8. Вычислить 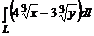 , где L- дуга астроиды
, где L- дуга астроиды 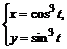 от точки А(1, 0) до точки В(0, 1).
от точки А(1, 0) до точки В(0, 1).
9. Вычислить 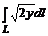 , где L- первая арка циклоиды
, где L- первая арка циклоиды 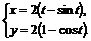
10. Вычислить 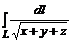 , где L- отрезок прямой от точки А(0, -2, 1) до точки В(4, 0, 2).
, где L- отрезок прямой от точки А(0, -2, 1) до точки В(4, 0, 2).
11. Вычислить 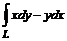 , где L – дуга астроиды
, где L – дуга астроиды 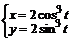 от точки А(2, 0) до точки В(0, 2).
от точки А(2, 0) до точки В(0, 2).
12. Вычислить 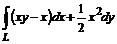 , где L – дуга параболы
, где L – дуга параболы 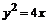 от точки А(0, 0) до точки В(1, 2).
от точки А(0, 0) до точки В(1, 2).
13. Вычислить 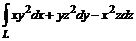 , где L – отрезок прямой от точки О(0, 0, 0) до точки В(-2, 4, 5).
, где L – отрезок прямой от точки О(0, 0, 0) до точки В(-2, 4, 5).
14. Вычислить 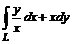 , где L – дуга линии
, где L – дуга линии  от точки А(1, 0) до точки В(е, 1).
от точки А(1, 0) до точки В(е, 1).
15. Вычислить 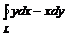 , где L – дуга эллипса; обход контура совершается против движения часовой стрелки.
, где L – дуга эллипса; обход контура совершается против движения часовой стрелки.
16. Вычислить 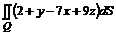 , где Q – часть плоскости
, где Q – часть плоскости 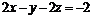 , отсеченная координатными плоскостями.
, отсеченная координатными плоскостями.
17. Вычислить 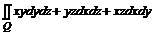 , где Q – внешняя сторона сферы
, где Q – внешняя сторона сферы 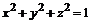 , лежащая в первом октанте.
, лежащая в первом октанте.
|
|
|
18. Вычислить 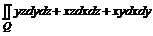 , где Q – часть плоскости
, где Q – часть плоскости 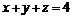 , лежащая в первом октанте (нормаль внешняя).
, лежащая в первом октанте (нормаль внешняя).
19. Вычислить 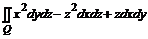 , где Q – часть поверхности параболоида
, где Q – часть поверхности параболоида 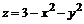 , отсекаемая плоскостью
, отсекаемая плоскостью 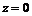 (нормаль внешняя).
(нормаль внешняя).
20. Вычислить поток векторного поля 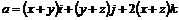 через внешнюю поверхность пирамиды, образуемой плоскостью
через внешнюю поверхность пирамиды, образуемой плоскостью 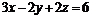 и координатными плоскостями.
и координатными плоскостями.
21. Вычислить поток векторного поля 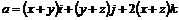 через часть плоскости
через часть плоскости 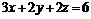 , отсеченной координатными плоскостями, нормаль к плоскости образует острый угол с осью Oz.
, отсеченной координатными плоскостями, нормаль к плоскости образует острый угол с осью Oz.
22. Вычислить поток векторного поля  через всю поверхность тела
через всю поверхность тела 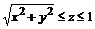 в направлении внешней нормали.
в направлении внешней нормали.
23. Вычислить 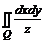 , где Q – внешняя сторона сферы
, где Q – внешняя сторона сферы 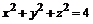 .
.
24. Вычислить циркуляцию векторного поля 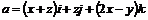 по контуру треугольника, полученного в результате пересечения плоскости
по контуру треугольника, полученного в результате пересечения плоскости 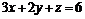 с координатными плоскостями, при положительном направлении обхода относительно нормального вектора.
с координатными плоскостями, при положительном направлении обхода относительно нормального вектора.
25. Вычислить циркуляцию векторного поля 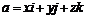 по окружности, полученной в результате пересечения сферы
по окружности, полученной в результате пересечения сферы 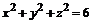 с плоскостью
с плоскостью 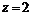 , при положительном направлении обхода относительно нормального вектора плоскости.
, при положительном направлении обхода относительно нормального вектора плоскости.
26. Найти ротор и дивергенцию векторного поля 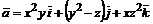 в точке М(1, -1, 2).
в точке М(1, -1, 2).
27. Для скалярного поля 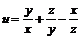 найти: а)
найти: а) 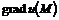 , если М(1, 1, 2); б) производную по направлению из точки М(1, 1, 2) в точку N(3, -1, 1).
, если М(1, 1, 2); б) производную по направлению из точки М(1, 1, 2) в точку N(3, -1, 1).
|
|
|
28. Для функции 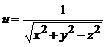 найти: а)
найти: а) 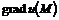 , если М(1, 2, 2); б) производную функции u по направлению из точки М(1, 2, 2) в точку О(0, 0, 0).
, если М(1, 2, 2); б) производную функции u по направлению из точки М(1, 2, 2) в точку О(0, 0, 0).
29. Выполнить операции, представить результат в алгебраической форме: а) 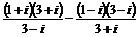 , б)
, б) 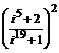 , в)
, в) 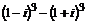 .
.
30. Вычислить: а) 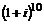 , б)
, б) 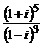 , в)
, в) 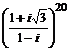 , г)
, г) 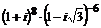 .
.
31. Найти и изобразить на комплексной плоскости все значения корней: а) 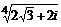 , б)
, б) 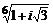 , в)
, в) 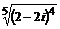 .
.
32. Решить уравнение: а) 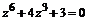 , б)
, б) 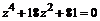 , в)
, в) 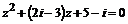 .
.
28. . Найти изображение функции: а) 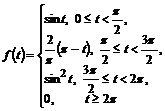 б)
б) 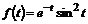 , в)
, в) 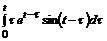 .
.
30. Найти оригинал: а) 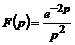 , б)
, б) 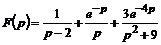 , в)
, в) 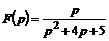 .
.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ
по дисциплине «Математический анализ 2»
Вариант № 0
1. Дифференциальные уравнения высшего порядка (основные понятия). Задача Коши.
2. Свойства преобразования Лапласа.
3. Вычислить поток векторного поля 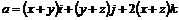 через часть плоскости
через часть плоскости 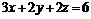 , отсеченной координатными плоскостями, нормаль к плоскости образует острый угол с осью Oz.
, отсеченной координатными плоскостями, нормаль к плоскости образует острый угол с осью Oz.
4. Найти частное решение дифференциального уравнения 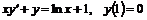 .
.
5. Решить уравнение 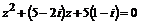 .
.
Дата добавления: 2018-06-01; просмотров: 93; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
