Элементы теории массового обслуживания
Рассматривается абстрактная модель, которую можно видеть на рис. 2.5, где λ – среднее число сообщений поступающих на вход в единицу времени.
| λ |
| Обслуживающий прибор |
| Очередь |
Рис. 2.5. Модель системы массового обслуживания
Каждая заявка обслуживается случайное время T. Среднее время обслуживания 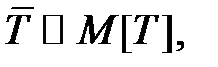 μ – интенсивность обслуживания, которая вычисляется по формуле
μ – интенсивность обслуживания, которая вычисляется по формуле 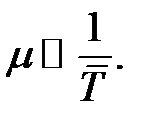
Рассмотрим случай, который продемонстрирован на рис. 2.6, где D1, D2 – время пребывания заявки в системе.
| 1 |
| 2 |
| 1 |
| 2 |
| D1 |
| D2 |
| t |
Рис. 2.6. Пример обслуживания заявок в системе
Если λ<μ, то система устойчива (средняя длина очереди конечна), если λ³μ, то система неустойчива (очередь постоянно накапливается), если λ=μ, то система устойчива только в том случае, если интервалы между поступлением заявок и интервалы времени между окончаниями обслуживания не случайны.
Для устойчивой системы можно определить задержку d, где 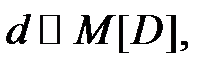 где D – время пребывания в очереди. Также задержку можно вычислить по формуле (т. Литтла)
где D – время пребывания в очереди. Также задержку можно вычислить по формуле (т. Литтла) 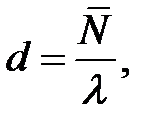 где
где 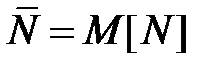 и
и 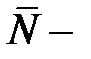 среднее число заявок в системе.
среднее число заявок в системе.
Система массового самообслуживания с постоянным временем обслуживания и пуассоновским входным потоком. Синхронная и асинхронная системы.
Данная система обозначается как M|D|1, где M – тип входного потока – простейший пуассоновский входной поток, D – закон распределения времени обсуживания, в данном случае - постоянная величина, 1 – число обслуживающих приборов. Существует 2 варианта системы – синхронная и асинхронная. На рис. 2.7. сверху представлена синхронная система, а под ней – асинхронная.
|
|
|
Для синхронной системы: все время работы системы разбито на интервалы одинаковой длины – окна. Длительность окна равна времени обработки одной заявки и это время приято за единицу времени. Обслуживание в такой системе может начаться только в начале окна. В LTE и многих других современных системах используются разделение на окна и именно синхронные системы.
В асинхронной системе обслуживание может начаться в любой момент времени. Первая заявка в системе начинает обрабатываться сразу же, в момент ее поступления.
Работу систем поясним диаграммой, которая изображена на рис 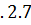 .
.
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| X4 4 |
| X3 |
| X1 1 X2 |
| 3 |
| ******* |
| 2 |
| * |
| ******* |
| ******* |
|
|
|
Рис.2.7. Временная диаграмма систем
Предполагается, что на вход системы поступает пуассоновский поток интенсивности 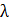 , т.е. среднее число заявок. X1, X2, X3, X4 – независимые случайные величины. Интервал времени между заявками распределен по экспоненциальному закону.
, т.е. среднее число заявок. X1, X2, X3, X4 – независимые случайные величины. Интервал времени между заявками распределен по экспоненциальному закону.
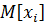 – средний интервал между заявками.
– средний интервал между заявками. 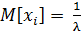 .
.
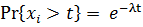 , т.к. величина распределена по экспоненциальному закону.
, т.к. величина распределена по экспоненциальному закону.
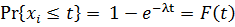 – интегрированная формула распределения.
– интегрированная формула распределения.
Формула плотности вероятности для экспоненциального распределения: 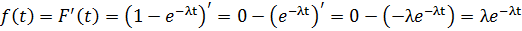 .
.
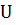 ~ равномерно распределенная от [0,1] случайная величина. X ~ F(t).
~ равномерно распределенная от [0,1] случайная величина. X ~ F(t).
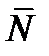
|
| p |
| 1 |
| 0 |
| 1 |
| X |
| U |
| F(t) |
Рис. 2.8 Интегрированная функция распределения
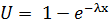
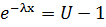
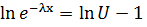
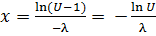 .
.
Выполним анализ асинхронной системы на качественном уровне. Положим  t задается от интенсивности входного потока.
t задается от интенсивности входного потока.
Для нахождения d0 рассмотрим ситуацию, когда в системе появляется одно единственное сообщение:
D
*
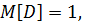 т.к. D = 1 = const и d0 = 1
т.к. D = 1 = const и d0 = 1
Для нахождения  кр воспользуемся утверждением:
кр воспользуемся утверждением:
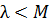 ,
, 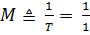 = 1
= 1
Тогда система устойчиво работает, если  < 1,
< 1, 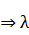 кр
кр 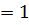
| d |
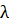
|
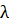 кр= 1
=1 кр= 1
=1
|
| d0 0 |
| 0 |
Рис. 2.9. Анализ асинхронной системы на качественном уровне
|
|
|
 кр = µ, d0=1
кр = µ, d0=1
Проведем анализ синхронной системы на качественном уровне.
Найдем d0. Для нахождения d0 рассмотрим ситуацию, когда в системе появляется заявка:
| D2 D |
| * |
| D1 |
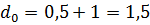
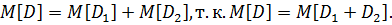

D1 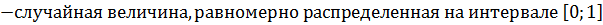
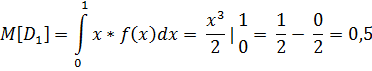
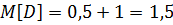
Для нахождения 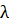 кр снова воспользуемся утверждением из теории массового обслуживания:
кр снова воспользуемся утверждением из теории массового обслуживания:
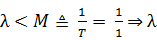 кр
кр 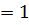
| Синхронная система |
| Асинхронная система |
| d |
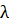 кр= 1
=1 кр= 1
=1
|
| 1 0 |
| 0 |
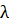
|
| 1,5 0 |
Рис. 2.10. Сравнительный анализ двух систем
2.6Анализ зависимости среднего числа заявок и средней задержки от интенсивности входного потока для синхронной системы M|D|1
1 допуск 3 лабораторной работы. Смоделировать синхронную и асинхронную систему M|D|1 и сравнить результаты моделирования с теоретическими формулами, которые будут получены далее.
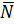 ≜
≜ 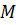
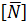 = f (
= f ( 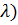
Смоделировать можно следующим образом:
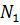 ,
, 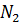 ..,
.., 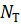 , где
, где 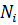 – число заявок в системе в -ый момент времени.
– число заявок в системе в -ый момент времени.
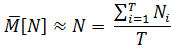
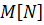 = lim
= lim 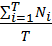
Предел существует при 
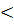 1. При
1. При  =0 предел существует и равняется 0.
=0 предел существует и равняется 0.
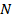
 > 1
> 1
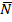
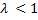
i
0 1 2 Т
КАК НАЗВАТЬ РИСУНОК?
|
|
|
Пусть к началу окна 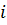 в системе было
в системе было 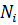 заявок и поступило
заявок и поступило 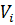 заявок. Покажем, как можно вычислить количество заявок
заявок. Покажем, как можно вычислить количество заявок 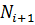 к началу следующего окна
к началу следующего окна 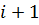 .
.
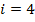
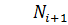
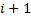
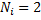
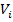 =3
=3
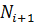 =
= 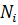 – 1 +
– 1 + 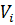
Скорректируем данное выражение. Необходимо учесть случай, когда в системе нет заявок.
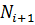 =
= 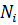 - I (
- I ( 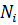 >0) +
>0) + 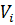 (1)
(1)
I – идентификатор события, если 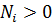 , то I = 1, иначе I = 0.
, то I = 1, иначе I = 0.
Замечание. Для любого момента времени 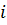
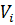 – случайные величины не зависят от
– случайные величины не зависят от 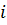 .
.
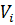
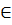
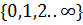
1 1 1 1
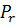 {x>t} =
{x>t} = 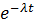 x x x
x x x
x1 x2 x3
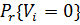 =
= 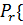 x>1
x>1 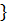 =
= 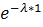
Значит в I момент времени не должно быть заявки.
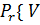 =n} =
=n} = 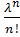
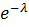 – распределение Пуассона.
– распределение Пуассона.
Интервалы времени разделены по экспоненциальному закону. Число заявок, поступающих через фиксированное время, распределено по закону Пуассона. Если рассматривать систему обслуживания на примере магазина, закон работает в случае, если желание людей подойти к кассе никак не скоординировано.
M 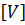 =
= 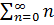 ·
· 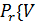 =n
=n 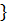 =
= 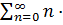
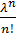
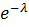 =
= 
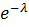 = 1 (как суммы всех возможных вероятностей) =
= 1 (как суммы всех возможных вероятностей) = 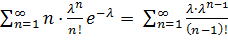
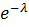 =
=
 ·
· 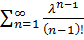
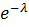 =|
=| 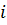 = n – 1 (замена)| =
= n – 1 (замена)| = 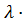
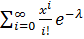 =
= 
M 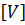 =
= 
D 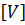 = M
= M 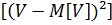 =
= 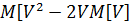 +
+ 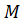 ²
² 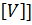 =
= 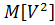 -
- 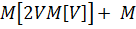 ²
² 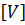 =
= 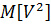 - 2
- 2 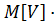
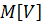 +
+ 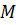 ²
² 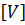 =
= 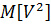 -
- 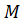 ²
² 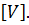
D 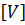 =
= 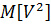 -
-  ²
²
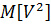 =
= 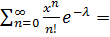
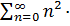
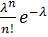 =
= 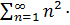
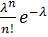 =
= 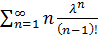
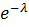 =
= 
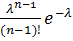 =
= 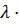
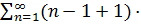
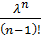
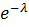 =
= 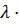

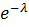 +
+ 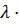
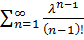
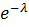 = |
= | 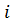 =n – 1(замена)| =
=n – 1(замена)| = 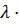
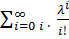
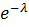 +
+ 
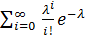 =
=  +
+ 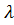
Получим, что D 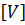 =
= 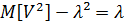 ²+
²+ 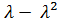 =
=  .
.
Замечание. Для Пуассоновского распределения D и M имеют одно численное значение.
Анализ (1) будет предполагать:
1)  <1, то есть система устойчива
<1, то есть система устойчива
2)Наблюдаем работу системы в бесконечный момент t 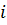
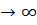
3) из п.1-2  M [
M [ 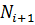 ] = M [
] = M [ 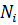 ]
]
Вспомним:
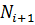 =
= 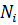 – I (
– I ( 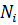 >0)+
>0)+ 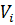 (*)
(*)
M[ 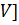 =
=  , D[
, D[ 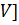 =
= 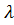
 <1,
<1, 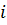
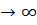
Возьмем мат.ожидание от правой и левой части (*).
M [ 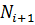 ] = M [
] = M [ 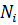 ] - M[I(
] - M[I( 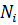 >0)] + M[
>0)] + M[ 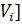 .
.
Было получено, что 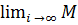 [
[ 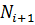 ] =
] = 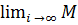 [
[ 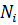 ], поэтому можно сократить. В дальнейшем индекс
], поэтому можно сократить. В дальнейшем индекс 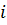 будем опускать для краткости обозначения, т.к. рассматриваем момент времени
будем опускать для краткости обозначения, т.к. рассматриваем момент времени 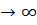 .
.
M[I( 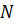 >0)] = M [
>0)] = M [ 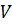 ]=
]= 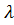
Pr { 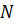 >0} =
>0} = 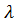 - вероятность того, что система не пустая, где
- вероятность того, что система не пустая, где  <1.
<1.
Если 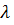 ≥ 1, то Pr {
≥ 1, то Pr { 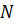 >0}=1.
>0}=1.
Возведем правую и левую часть (*) в квадрат (индекс 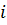 будем опускать, так как
будем опускать, так как 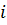
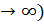 .
.
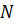 ² =
² = 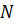 ²+ I² (
²+ I² ( 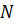 >0)+
>0)+ 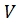 ² - 2
² - 2 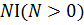 +2
+2 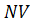 - 2
- 2 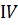 .
.
Возьмем мат. Ожидание
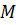 [
[ 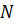 ²] =
²] = 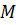 [
[ 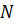 ²]+
²]+ 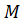 [
[ 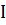 ²(
²( 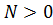 )]+
)]+ 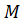 [
[ 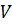 ²] - 2
²] - 2 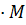 [
[ 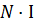 (
( 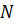 >0)]+2
>0)]+2 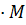 [
[ 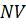 ] – 2
] – 2 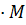 [
[ 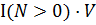 ] (**)
] (**)
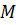 [
[ 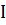 ²
² 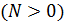 ]=
]= 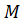 [
[ 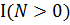 ], так как
], так как 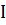 – случайная величина, которая принимает 2 значения: 0 и 1, а 0²=0 и 1²=1.
– случайная величина, которая принимает 2 значения: 0 и 1, а 0²=0 и 1²=1.
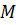 [
[ 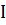 ²
² 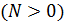 ]=
]= 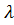
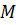 [
[ 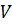 ²]=
²]= 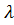 ²+
²+ 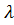
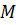 [
[ 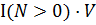 ]=
]= 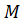 [
[ 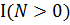 ]
] 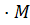 [
[ 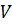 ] =
] =  ²
²
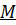 [
[ 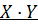 ]=
]= 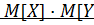 ], если случайные величины – независимые.
], если случайные величины – независимые.
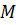 [
[ 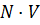 ]=
]= 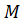 [
[ 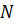 ]
] 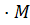 [
[ 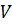 ]=
]= 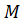 [
[ 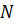 ]
] 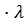 =
= 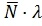
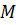 [
[  ]=
]= 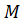 [
[ 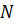 ]=
]= 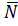
Зависимые случайные величины
 =
= 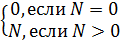 =>
=> 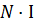
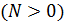 =
= 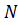
Получаем:
O= 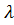 +(
+( 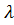 ²+
²+ 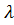 ) - 2
) - 2 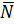 +2
+2  - 2
- 2 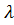 ²
²
-2 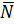 +2
+2  =2
=2 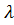 ² -
² -  -
-  ² -
² - 
2 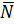 (
(  – 1)=
– 1)= 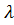 ² - 2
² - 2 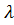
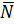 =
= 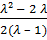 =
= 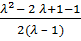 =
= 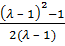 =
= 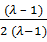 -
- 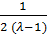 =
= 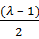 -
- 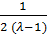
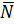 =
= 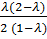
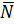 =
= 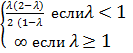
В итоге получили зависимость 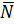 от
от  :
: 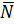 =
= 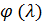
Но нас интересует : d=f ( 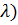 =
= 
d( 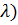 асинхр =
асинхр = 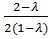 при
при 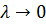 ,
, 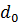 =1
=1
Данная формула справедлива для асинхронной системы, так как обслуживание начинается сразу с момента поступления заявки.
Для синхронной системы: d( 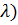 синхр=
синхр= 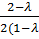 +
+  =
= 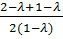 =
= 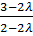 .
.
Дата добавления: 2018-06-01; просмотров: 792; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
