C)Стрелка Пирса, штрих Шеффера и разность
На рис. 1.7 и 1.8 приведены диаграммы двух новых операций, которые называются, соответственно, стрелка Пирса и штрих Шеффера. Эти диаграммы дополняют объединение и пересечение до фундаментального множества V.
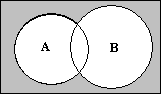 Рис. 1.7 Рис. 1.7
| 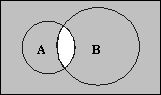 Рис. 1.8 Рис. 1.8
|
На множествах эти операции выглядят следующим образом:
A ¯ B = {1, 2, 4, 6} ¯ {2, 3, 4, 8, 9} = {5, 7, 10, 11} = C0,
A | B = {1, 3, 5, 6, 7, 8, 9, 10, 11} = C0 È C1 È C2.
D)Разность
Разностью между множествами A и B называется совокупность тех элементов множества A, которые не вошли во множество B:
A – B = {1, 2, 4, 6} – {2, 3, 4, 8, 9} = {1, 6} = C1.
Диаграмма Эйлера — Венна для нее приведена на рис. 1.9.
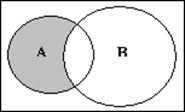
Рис. 1.9
На диаграмме Эйлера — Венна для импликации (рис. 1.10) показано частичное включение множества A во множество B, которое нужно отличать от полного включения (рис. 1.2).
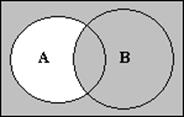
Рис. 1.10
Если утверждается, что «элементы множества A включены во множество B», то область C3 обязательно должна быть заштрихована, а область C1 с такой же необходимостью должна быть оставлена белой. Относительно областей C0 и C1, находящихся в A, заметим, что мы не имеем права оставлять их белыми, но, мы обязаны все же области, попадающие в A, заштриховать.
Е)Симметрическая разность и эквивалентность
Остается привести еще две взаимно дополняющих операции — симметрическую разность и эквивалентность. Симметрическая разность двух множеств A и B есть объединение двух разностей:
|
|
|
A + B = (A – B) È (B – A) = C1 È C2 = {1, 3, 6, 8, 9}.
Эквивалентность определяется теми элементами множеств A и B, которые для них являются общими. Однако элементы, не входящие ни в A, ни в B, также считаются эквивалентными:
A ~ B = (A Ç B) È (A Ç B) = C0 È C3 = {2, 4, 5, 7, 10, 11}.
На рис. 1.11 и 1.12 показана штриховка диаграмм Эйлера — Венна.
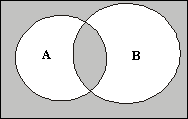 Рис. 1.11 Рис. 1.11
| 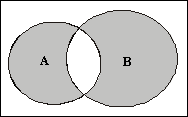 Рис. 1.12 Рис. 1.12
|
В заключение отметим, что симметрическая разность имеет несколько названий: строгая дизъюнкция, исключающая альтернатива, сумма по модулю два. Эту операцию можно передать словами — «либо А, либо В», т.е. это логическая связка «или», но без включенной в нее связки «и».
Заключение
Диаграммы Эйлера-Венна – геометрические представления множеств. Простое построение диаграммы обеспечивает наглядное изображение, представляющее универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры пересекаются в наиболее общем случае, требуемом в задаче, и соответствуют образному изображению. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств. Это позволяет нам иметь наиболее полное представление о задаче и ее решении. Простота диаграмм Эйлера-Венна позволяет использовать данный прием в таких направлениях, как математика, логика, менеджмент и других прикладных направлениях.
|
|
|
Список литературы
1. Словарь по логике. — М.: Туманит, изд. центр ВЛАДОС. А.А.Ивин, А.Л.Никифоров. 1997
2. Weisstein, Eric W. «Диаграмма Венна» (англ.) на сайте Wolfram MathWorld.
3. http://yandex.ru
Дата добавления: 2018-06-01; просмотров: 1398; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
