Потенциал взаимодействия молекул.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Для изучения связи между макроскопическими параметрами системы (температуры, давления и т.д.) и ее микроскопическими параметрами (размер, масса и скорость молекул или атомов, силы взаимодействия между ними) необходимо привлекать модельные представления. В зависимости от сложности модели мы можем описывать свойства макроскопических тел в том или ином приближении.

В курсе общей физики для описания свойств идеального газа молекулы его представляли упругими шарами бесконечно малых размеров; столкновение шаров-молекул происходит за бесконечно малый промежуток времени. Поэтому большую часть времени молекулы проводят в свободном полете, не испытывая взаимодействия между собой.

В модели реального газа Ван-дер-Ваальса, молекулы имеют ненулевые размеры и испытывают упругие столкновения. Молекулы взаимно притягиваются, но сила притяжения быстро убывает с расстоянием. По существу сказанное означает, что между двумя молекулами, удаленными на расстояние R имеет место потенциал U(R) взаимодействия. Наиболее употребительным является современное представление

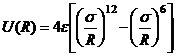, (4.1)

где e и s – константы.

Потенциал (4.1) называется потенциалом Леннарда – Джонса, его графическое представление U(R) приведено на рис. 4.1.

Так как сила F взаимодействия равна F = – dU/dR, то в точке R = R_min сила F = 0. Нетрудно проверить, что R_min = 2^1/6s. На расстояниях R > R_min, где dU/dR > 0 и F < 0, молекулы притягиваются (рис. 4.2). Наоборот, если R < R_min , то dU/dR < 0 и F > 0 и между молекулами происходит отталкивание.

Можно считать, что потенциал U(R) Леннарда – Джонса состоит из притягивающей U₊ ~ R^–6 и отталкивающей U_– ~ R^–12 частей.

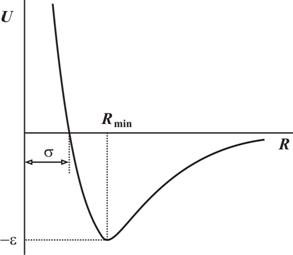
Рис. 4.1. График функции потенциала Леннарда – Джонса.

На рис. 4.2 молекулы изображены кружочками (с конкретными размерами) только для наглядности. На самом деле, согласно (4.1), они не обладают какими-либо конкретными размерами.

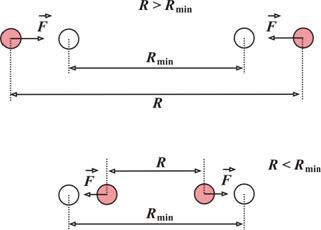
Рис. 4.2Притягивание при R > R_min и отталкивание при R < R_min молекул, согласно потенциалу Леннарда – Джонса.

Но по мере приближения (R ® 0) молекул сила отталкивания настолько быстро возрастает (~ 1/R¹²), что в скором времени полная кинетическая энергия налетающих друг на друга частиц полностью перейдет в потенциальную энергию, и в последующем частицы начнут разлетаться. При этом половину расстояния максимального сближения можно условно принять за размер молекул, т.к. это расстояние, вообще говоря, зависит от начальной кинетической энергии сталкивающихся молекул.

Вандерваальсово взаимодействие всегда существует между близко расположенными атомами, но играет важную роль лишь в отсутствие более сильных механизмов связи. Сила Ван-дер-Ваальса имеет частично электростатическую и частично квантово-механическую природу.

Согласно квантовой теории микрочастицы имеют нулевые колебания – движения, не прекращающиеся даже при абсолютном нуле температуры в силу принципа неопределенности. Нулевые колебания создают у каждого электрически нейтрального атома флуктуирующий дипольный момент с быстро меняющейся ориентацией и амплитудой. Поле, индуцируемое диполем, убывает пропорционально кубу расстояния. Таким образом, если ядра двух атомов находятся на расстоянии r друг от друга, диполь одного из атомов в каждый момент времени создает в точке, где находится другой диполь, мгновенное поле, пропорциональное 1/r³. При этом потенциальная энергия взаимодействия между диполями, приводящая к притяжению (второй член в формуле (4.1)), определяется как

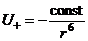С уменьшением расстояния между атомами электронные облака атомов начинают перекрываться, возникает механизм, приводящий к ослаблению притяжения. Это можно понять с помощью принципа Паули, согласно которому в одном и том же квантовом состоянии не может находиться не более одного электрона. Таким образом, перекрытие электронных облаков двух атомов с почти заполненными электронными оболочками возможно лишь при переходе некоторых электронов в более высокие квантовые состояния или на более высокие орбиты, для чего требуется дополнительная энергия. Это обстоятельство проявляется как наличие силы отталкивания между атомами с потенциалом

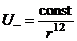Потенциал Леннарда-Джонса применяется при моделировании многих систем, и на его основе проверена справедливость многих научных гипотез, нашли теоретическое объяснение множество экспериментальных фактов, рассчитаны важные кинетические параметры газов и жидкостей. Тем не менее, этот потенциал является лишь приближенным представлением формы и характера взаимодействия атомов и молекул. Наиболее точные результаты получаются для атомов аргона.

Уравнения движения.

В качестве примера рассмотрим четыре произвольные молекулы, положения их в лабораторной системе координат определяются радиус-векторами r₁, r₂, r₃, r₄ (рис. 4.3).

Без потери физического содержания рассматриваемого вопроса можно считать все движения происходящими на плоскости. Согласно второму закону Ньютона

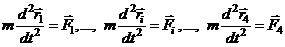, (4.2)

где F_i – сумма сил, действующих на частицу с номером i со стороны всех остальных частиц. Правые и левые части каждого уравнения из (4.2) можно записать в проекциях на оси координат x, y:

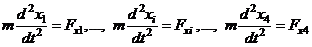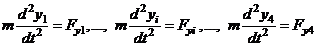где F_xi, F_yi – проекции на оси координат силы F_i, и использовано определение радиус-вектора .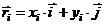

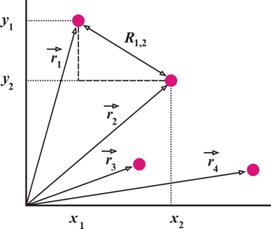
Рис. 4.3. Расположение 4 частиц на плоскости и их радиус-векторы.

Каждая из сил F_xi, F_yi складывается из частных сил 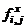(из соображений удобства индекс x мы будем писать сверху), действующих на частицу i со стороны всех остальных. Найдем силу 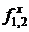, действующей на частицу 1 со стороны частицы 2. Потенциал U_{1, 2} взаимодействия молекул 1 и 2 равен

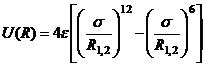где R_1,2 – расстояние между молекулами 1 и 2:

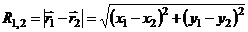что следует из теоремы Пифагора. Тогда x – компонента силы 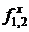, равна

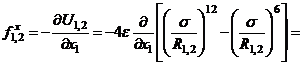
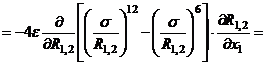
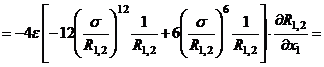
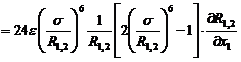Вычислим производную

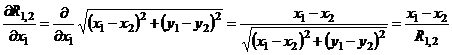Тогда искомой силы получаем выражение

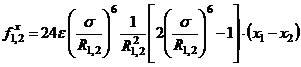. (4.3)

С физической точки зрения частица 3 отличается от частицы 2 только лишь номером. Поэтому легко сообразить, что выражение для силы 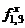, действующей на частицу 1 со стороны частицы 3, можно получить из формулы (4.3) простой заменой индекса 2 на индекс 3:

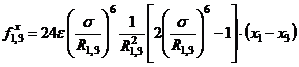где расстояние между частицами 1 и 3 определено как

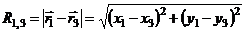Такой же процедурой получается и 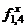. И вообще в случае N частиц

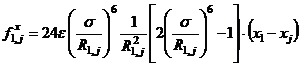, (4.4)

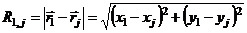, j = 2, 3, 4, …, N.

Таким образом, для случая четырех частиц-молекул уравнение движения для частицы 1 имеет вид

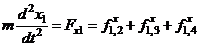. (4.5)

Запишем теперь уравнение движения для частицы 2. Сила, действующая на частицу 2 со стороны частицы 1, есть 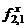. Она, согласно третьему закону Ньютона, численно равна силе 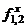, взятой с обратным знаком:

f ^x_2,1 = – f ^x_1,2,

в чем легко убедиться, переставив в (4.3) местами индексы 1 и 2. Перестановка индексов, как математическая процедура, имеет при этом ясный физический смысл – это перестановка частиц местами; расстояние между частицами не меняется: R_2,1 = R_1,2. Силы же, действующие на частицу 2 со стороны частиц 3 и 4 можно найти, не прибегая к вычислениям по аналогии с формулой (4.4), заменив индекс 1 на 2:

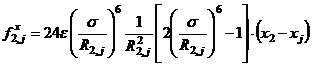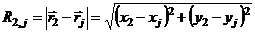Данный факт является следствием тождественности всех молекул как физических объектов. Все рассматриваемые молекулы в данном контексте отличаются только лишь координатами, а любые две точки пространства эквивалентны по физическим свойствам, т.е. пространство однородно и изотропно.

Таким образом, уравнение движения (вдоль оси x) для второй частицы будет следующим:

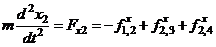. (4.6)

Глядя на формулы (4.5) и (4.6) можно догадаться, как будут выглядеть уравнения движения вдоль координаты x для частиц 3 и 4. В итоге имеем

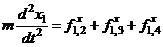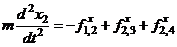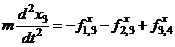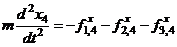Правые части выписанных уравнений можно записать в компактной форме. Такая форма очень важна при численных расчетах для организации вычислении. Нетрудно видеть, что

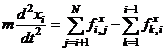, (4.7)

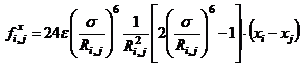Здесь хотя и число N = 4, но формулы (4.7) на самом деле справедливы при произвольных значениях N.

Далее, ввиду того, что в нашей системе молекул физические процессы эквивалентны вдоль координатных осей x и y, то ни одна из этих координат не является «выделенной». Простой поворот системы координат при неизменных положениях молекул с результатом перехода x ® y или наоборот, не приведет к изменению характера движения и столкновении (взаимодействия) молекул. Иначе обстояло бы дело, если бы наша система частиц-молекул находилась во внешнем поле (например, гравитационном), существенно меняющемся на масштабах порядка размеров системы. Здесь слово «существенно» означает сравнимость по численной величине изменения потенциальной гравитационной энергии частиц на разных границах системы с их (средней) кинетической энергией.

Раз мы предполагаем отсутствие (или малость в смысле вышесказанного) внешних потенциальных сил, то уравнения движения вдоль оси y могут быть получены из (4.7) простой заменой x ® y:

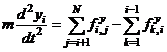, (4.8)

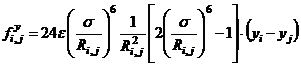Выражения (4.7) и (4.8) представляют собой искомую систему уравнений движения частиц на плоскости.

Дата добавления: 2018-06-01; просмотров: 1148; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!