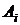Варианты индивидуальных заданий

Лабораторная работа №1

Тема « Линейная регрессия»

Цель работы:научить студентов строить парные линейные регрессионные модели.  

Задание

1. Рассчитайте параметры уравнения линейной парной регрессии.

2. Оценить адекватность линейной модели с помощью показателей корреляции и детерминации, средней ошибки аппроксимации, F-критерия Фишера.

 

Пример выполнения лабораторной работы

Исходные данные

По территориям 10 регионов (i – номер региона) известны данные за год по среднедневной заработной плате (y, руб.) и среднедушевому прожиточному минимуму в день одного трудоспособного (x, руб.):

i	1	2	3	4	5	6	7	8	9	10
x	67	65	82	77	90	87	88	61	69	79
y	117	108	125	118	137	130	141	107	108	116

 

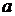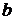1. Для расчета параметров  и  линейной регрессии  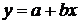составим следующую таблицу (табл. 1).

Таблица  1

Район
1	67	117	7839	4489	13689	110,5218	5,5369
2	65	108	7020	4225	11664	108,379	0,3509
3	82	125	10250	6724	15625	126,5927	1,2741
4	77	118	9086	5929	13924	121,2357	2,7421
5	90	137	12330	8100	18769	135,1638	1,3402
6	87	130	11310	7569	16900	131,9496	1,4997
7	88	141	12408	7744	19881	133,021	5,6588
8	61	107	6527	3721	11449	104,0934	2,7164
9	69	108	7452	4761	11664	112,6646	4,3190
10	79	116	9164	6241	13456	123,3785	6,3607
Среднее	76,5	120,7	9338,6	5950,3	14702,1		3,1799
Дисперсия	98,05	133,61
Ср.кв.откл.	9,90202	11,55898

 

Опишем последовательность  расчета таблицы 1 с помощью ППП Exel.

1) Вводим исходные данные в первые три столбца нового листа (Рис.1):

                                                                                                                     

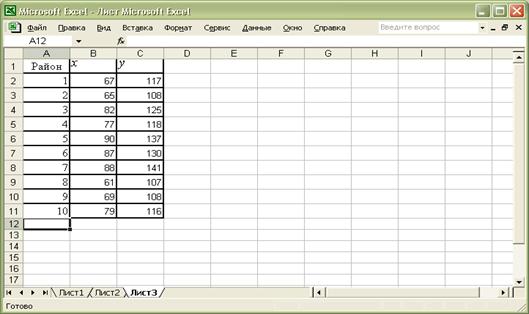
Рис.1

2) Для расчета столбца 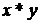 выполним следующую последовательность действий:

Устанавливаем курсор в ячейку D2 двойным щелчком левой кнопке мыши по данной ячейке; 

Вводим знак равенства в ячейке D2;

Щелкаем по ячейке B2;

Вводим знак умножения *;

Щелкаем по ячейке С2 (Рис.2);

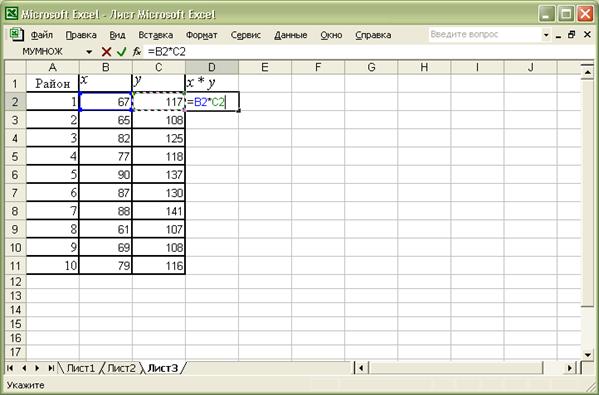
Рис.2

Нажимаем клавишу Enter (Рис 3).

Рис.3

Выделяем ячейку D2 и подводим курсор к правому нижнему углу этой ячейки. Курсор должен принять форму тонкого черного знака плюс (Рис 4.)

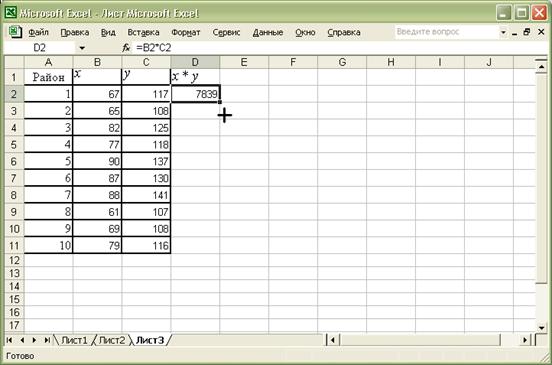
Рис 4.

Для оставшихся ячеек столбца D применим функцию автозаполнения. Для этого, удерживая правый нижний угол ячейки D2, протягиваем курсор до конца столбца (Рис 5).

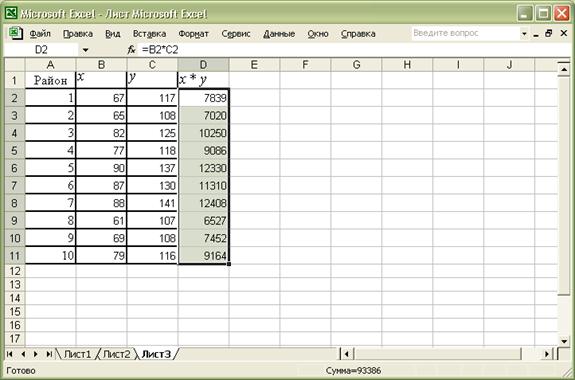
Рис. 5

3) Для расчета значений столбца 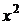 выполним следующую последовательность действий:

Устанавливаем курсор в ячейку С2 двойным щелчком левой кнопке мыши по данной ячейке; 

Вводим знак равенства в ячейке С2;

Щелкаем по ячейке B2;

Вводим знак возведения в степень ^ и цифру 2 (Рис. 5);

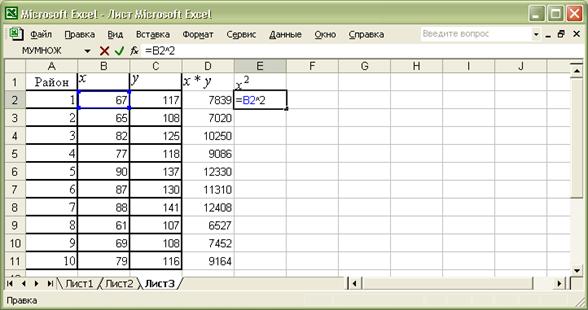
Рис. 5.

Нажимаем клавишу Enter;

Для оставшихся ячеек столбца Е применим функцию автозаполнения. Для этого выделяем ячейку Е2 и подводим курсор к правому нижнему углу этой ячейки. После того, как курсор принял форму тонкого черного знака плюс, удерживая правый нижний угол ячейки Е2, протягиваем курсор до конца столбца.

4)  Аналогично п.3 рассчитываем столбец .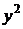

5)   Рассчитаем средние значения. Двойным щелчком левой кнопки мыши по ячейке B12 входим в режим её редактирования и пишем знак равенства. Затем щелкаем по значку  (вставка функции), находящемуся в командной строке под главным меню Exel (Рис.6):

 

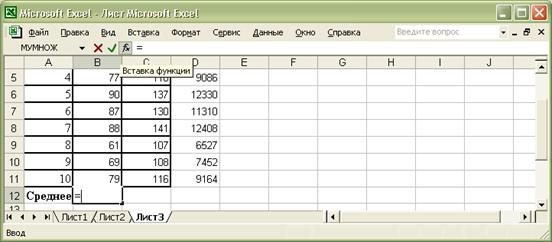
Рис 6.

Открывается диалоговое окно мастера функций. Выбираем функцию СРЗНАЧ из категории «Статистические»( Рис. 7):

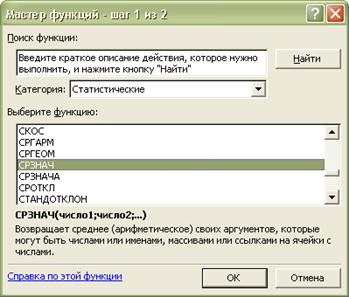
Рис. 7

Нажимаем кнопку ОК. Появляется окно выбора диапазона значений

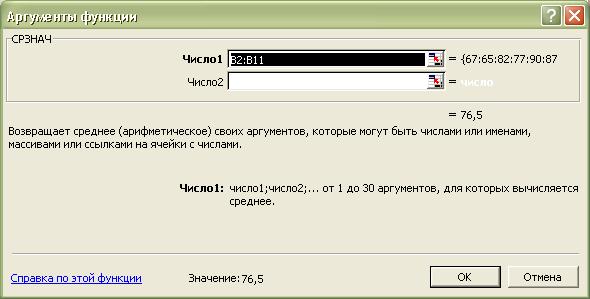
По умолчанию Exel предложил диапазон B2:B11  для расчета среднего значения. Если бы диапазон данных, предложенный по умолчанию, не совпал с тем, что мы собирались рассчитать, мы бы поменяли его, выделив требуемые данные мышью. Но поскольку это именно то, что нам нужно, мы нажимаем кнопку ОК. В ячейке B12 появляется среднее значение по столбцу 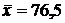 (Рис.8):

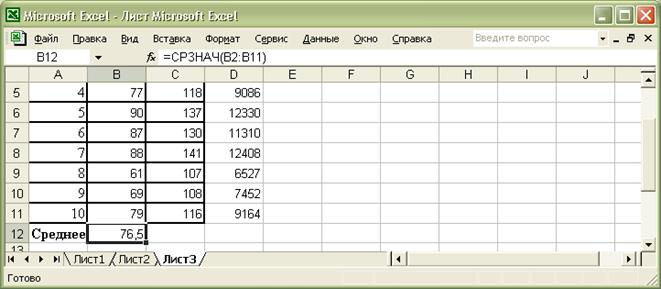
Рис.8

6)  Аналогично рассчитываем величины , , , , 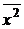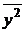как средние значения по столбцам , , , .

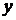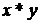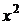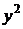7)  Дисперсия  фактора 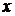 определяется по формуле 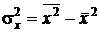. Аналогично вычисляется дисперсия фактора 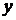: 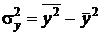. Среднеквадратическое отклонение  есть корень квадратный из дисперсии. Таким образом, для расчета дисперсии фактора  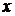следует выполнить следующую последовательность действий: 

Вводим знак равенства в ячейке B13 (Рис. 9) :

Рис. 9

Щелкаем по ячейке Е12, вводим минус, щелкаем B12, набираем ^2  (Рис. 10):

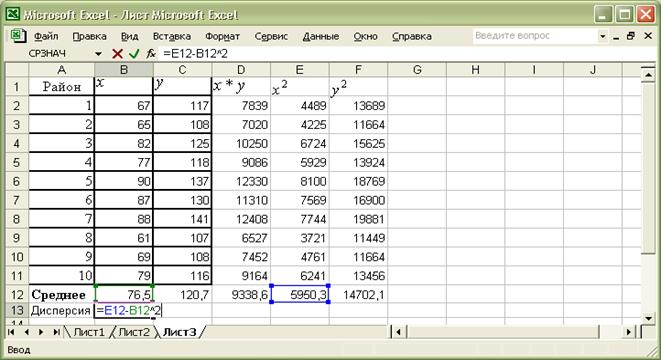
Рис.10.

Нажимаем Enter. В ячейке B13  появляется значение дисперсии фактора : .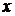

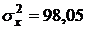8) Рассчитаем среднеквадратическое отклонение фактора 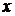. Для этого введем знак равенства в ячейке B14 и  щелкнем по значку (вставка функции), находящемуся в командной строке. В открывшемся диалоговом окне выберем  функцию КОРЕНЬ из категории Математические (Рис. 11):

Рис.11

Нажимаем ОК. Открывается диалоговое окно выбора аргумента функции (Рис. 12):

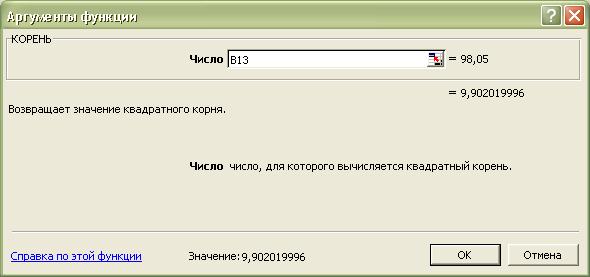
Рис. 12

По умолчанию окошко «Число» окажется незаполненным. Чтобы в нем появилась ссылка на значение, из которого необходимо выделить корень квадратный, в данном случае  дисперсии фактора 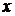, щелкнем по соответствующей ячейке  B13. Затем нажимаем кнопку ОК, и в ячейке B14 появляется значение среднеквадратического отклонения фактора : .

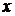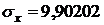9)  Аналогично рассчитываем дисперсию 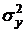 и среднеквадратическое отклонение  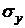фактора .

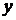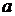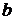10)  Рассчитаем параметры и  линейной регрессии .

,

.

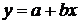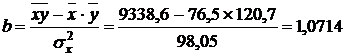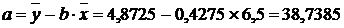Итак, уравнение линейной регрессии имеет вид .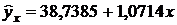

2. Оценим адекватность линейной модели. Рассчитаем линейный коэффициент парной корреляции: .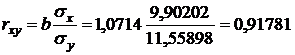

Связь сильная (так как ), прямая (так как ).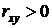

Коэффициент детерминации 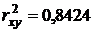, значит, вариация результата на 84,24% объясняется вариацией фактора 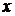, а на 15,76% – вариацией неучтенных в модели признаков.

Рассчитаем в таблице столбец теоретических (расчетных) значений 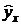 фактора  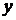путем подстановки  в полученное уравнение регрессии фактических значений 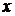. Для этого в ячейку G2 вводим знак равенства и уравнение регрессии, подставляя в него вместо  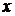ссылку на первое из значений фактора (Рис. 13)

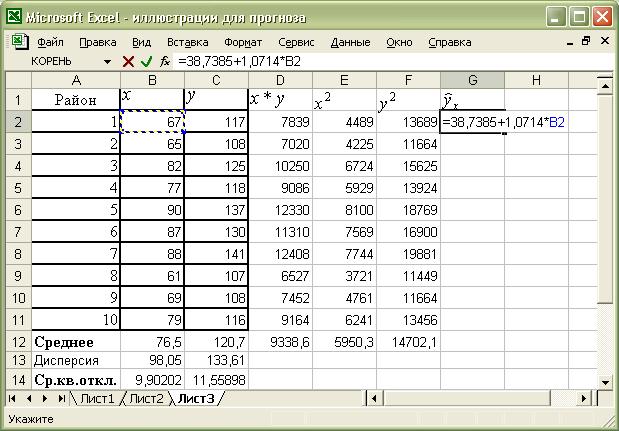
Рис.13

Нажимаем клавишу Enter и «автозаполняем» оставшиеся ячейки столбца, протягивая ячейку G2 за правый нижний конец. 

Средняя ошибки аппроксимации  определяется следующим образом:

,  где  (*)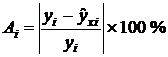

Для ее вычисления рассчитаем последний столбец 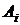 таблицы 1. В ячейку H2 вводим знак равенства и формулу (*) (Рис.14):

Рис.14

Нажимаем клавишу Enter и «автозаполняем» оставшиеся ячейки столбца, протягивая ячейку H2 за правый нижний конец. Затем рассчитываем среднее значение по этому столбцу, которое и есть искомая величина средней ошибки аппроксимации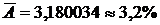

Таким образом, в среднем, расчетные значение от фактических отклоняются на 3,2 %, это говорит об удовлетворительном качестве модели, поскольку средняя ошибка аппроксимации не превышает 8–10 %.

 Оценим теперь статистическую надежность полученной модели с помощью F-критерия Фишера.

Выдвигаем гипотезу 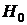 о статистической незначимости уравнения регрессии и показателя тесноты связи:

.

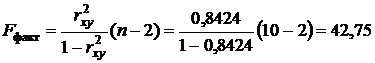Определяем по таблице значений F-критерия Фишера (Приложение 1) 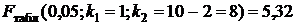. Так как 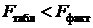, то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.

 

Варианты индивидуальных заданий

1. По территориям некоторых регионов (i – номер региона) известны данные за год по среднедневной заработной плате (y, руб.) и среднедушевому прожиточному минимуму в день одного трудоспособного (x, руб.):

i	1	2	3	4	5	6	7	8	9	10
x	95	107	125	111	89	97	65	131	92	102
y	162	151	190	178	161	175	144	191	160	161

 

2. Имеются данные о цене однокомнатной квартиры и величине ее общей площади по 10 сделкам одного района города:

i	1	2	3	4	5	6	7	8	9	10
x	35	35	33	34	38	40	40	39	37	36
y	29	31	35	35	45	46	45	44	38	37

 

3. По однородным предприятиям (i – номер предприятия) имеются данные о количестве рабочих с профессиональной подготовкой (x, %) и количестве бракованной продукции (y, %):

i	1	2	3	4	5	6	7	8	9	10
x	39,4	40,1	48,6	54,7	58,4	70,5	85,1	65,3	57,3	50,6
y	17,1	18,3	11,2	9,3	10,8	5,9	3,8	6,7	8,4	9,5

 

4. Компания «Вест», состоящая из 12 региональных представительств (i – номер представительства), продает кухонные принадлежности, рассылая каталоги по почте. Данные, иллюстрирующие количество рассылок (x, тыс. адресов) и объем выручки региональных представительств компании (y, млн у.е.):

i	1	2	3	4	5	6	7	8	9	10	11	12
x	65	55	67	41	59	78	105	110	125	91	47	93
y	28	19	20	17,5	20	24,5	29,5	31	35	30	18,5	27

 

5. Имеются данные о количестве копий (x, тыс. шт.), сделанных копировальными машинами различных марок в издательских центрах города и стоимости технического обслуживания копировальных машин (y, тыс. у.е.):

i	1	2	3	4	5	6	7	8	9	10	11	12
x	16	19	24	26	28	29	33	39	40	41	44	45
y	1,4	1,6	1,7	1,75	1,85	2,4	2,7	2,8	2,8	2,7	2,9	3

   

6. Имеются данные по 12 группам населения о среднегодовом доходе и уровне потребления мяса жителями штата Канзас (США):

i	1	2	3	4	5	6	7	8	9	10	11	12
x	41,2	35,3	40,7	55,1	80,1	65,9	64,2	70,5	61,1	51,7	59,4	65,8
y	41,5	29,6	31,8	69,8	100,5	93,3	82,1	77,4	55,7	38,9	45,2	60,2

 

 

7. По территориям некоторых регионов (i – номер региона) известны данные за год по среднедневной заработной плате (y, руб.) и среднедушевому прожиточному минимуму в день одного трудоспособного (x, руб.):

i	1	2	3	4	5	6	7	8	9	10
x	85	91	115	111	94	115	95	130	90	122
y	131	124	152	150	139	157	129	160	125	153

         

8. Имеются данные по 10 хозяйствам (i – номер хозяйства) по урожайности (y, ц/га) и количеству внесенных удобрений (x, кг/га):

i	1	2	3	4	5	6	7	8	9	10
x	2,1	3,6	3,5	5,0	6,5	4,2	6,3	4,0	6,0	7,5
y	15	18	17	22	25	20	24	19	23	27

         

9. Администрация страховой компании приняла решение о введении нового вида услуг – страхования на случай пожара. С целью определения тарифов по выборке анализируется зависимость стоимости ущерба                (y, млн руб.), нанесенного пожаром, от расстояния до ближайшей пожарной станции (x, км):

i	1	2	3	4	5	6	7	8	9	10
x	4,5	3,8	5,1	4,8	10,1	8,2	6,1	9,2	3,1	2,1
y	25,0	38,9	68,1	75,4	91,4	55,3	40,7	79,3	88,8	19,1

         

10. Компанию по прокату автомобилей интересует зависимость между пробегом (y, тыс. км) автомобилей и стоимостью ежемесячного обслуживания (x, у.е.):

i	1	2	3	4	5	6	7	8	9	10	11	12
x	15	17	26	20	24	25	18	21	24	20	30	12
y	8	11	31	15	27	30	13	17	21	23	35	9

       

11. Имеются данные о годовой цене программы «Мастер делового администрирования» (y, тыс. долл.) и числе слушателей в образовательном учреждении (x):

i	1	2	3	4	5	6	7	8	9	10	11	12
x	5	10	12	15	20	22	25	30	35	36	40	50
y	8,0	5,0	4,9	4,0	3,8	3,5	3,8	3,7	3,6	3,5	3,4	3,0

        

12. Исследуется зависимость между урожайностью зерновых (y, ц/га) и количеством внесенных удобрений на 1 га посевов. Данные по 11 фермерским хозяйствам области (x, кг):

i	1	2	3	4	5	6	7	8	9	10	11
x	12	18	25	19	23	17	11	19	14	18	11
y	29	36	41	48	46	31	25	22	38	32	26

        

13. При исследовании годового дохода (y, тыс. у.е.) и сбережений населения (x, тыс. у.е.) получены следующие данные:

i	1	2	3	4	5	6	7	8	9	10
x	8	13	9	3	4	15	16	20	15	17
y	59	83	55	47	39	97	125	150	74	71

14. По территориям некоторых регионов (i – номер региона) известны данные за год по среднедневной заработной плате (y, руб.) и среднедушевому прожиточному минимуму в день одного трудоспособного (x, руб.):

i	1	2	3	4	5	6	7	8	9	10
x	98	98	118	103	95	121	99	114	93	107
y	118	111	126	114	118	129	126	122	105	113

         

15. Изучается зависимость между ценой квартиры (y, тыс. долл.)        и размером общей площади (x, м²) по данным, представленным в таблице:

i	1	2	3	4	5	6	7	8	9	10
x	200	89	127	130	195	112	130	75	74	48
y	89	44	76	69	130	83	65	37	33	22

         

16. Данные о тираже бесплатной рекламной газеты «Реклама для вас» (y, тыс. экз.), распространяемой в различных регионах РФ и стоимости размещения в ней рекламы стандартного размера (1/4 газетной полосы) (x, тыс. у.е.):

i	1	2	3	4	5	6	7	8	9	10	11	12
x	1,6	1,2	2	2,6	1,3	0,8	1,7	1,3	1,5	0,9	2,1	2,2
y	350	125	400	875	200	100	300	175	225	85	400	500

      

17. По 12 регионам страны изучается зависимость ежемесячного среднедушевого денежного дохода (y, тыс. руб.) от удельного веса населения в трудоспособном возрасте в общей численности населения (x, %):

i	1	2	3	4	5	6	7	8	9	10	11	12
x	59,2	59,6	60,8	59,4	60,4	59,2	61,0	59,3	60,3	60,2	59,0	61,4
y	3,4	3,1	3,7	3,4	3,6	3,4	3,9	3,3	3,6	3,2	3,3	4,1

       

18. По 13 регионам страны изучается зависимость ожидаемой продолжительности жизни при рождении (y, лет) от уровня заболеваемости детей в возрасте 0–14 лет на тысячу человек (x):

i	1	2	3	4	5	6	7	8	9	10	11	12	13
x	1108,4	1164,4	438,8	618,1	1312,4	1312,8	843,0	1233,6	1173	1415,5	1608,6	1703,9	1529,0
y	67,5	69,3	75,1	68,7	66,2	66,1	70,0	67,3	67,1	65,4	66,4	66,5	66,4

  

19. По территориям некоторых регионов (i – номер региона) известны данные за год по среднедневной заработной плате (y, руб.) и среднедушевому прожиточному минимуму в день одного трудоспособного (x, руб.):

i	1	2	3	4	5	6	7	8	9	10
x	88	87	110	101	93	118	93	111	93	102
y	120	112	133	123	126	140	131	133	114	120

         

20. По 10 регионам страны изучается зависимость розничной продажи телевизоров (y, шт.) от среднедушевых денежных доходов в месяц                 (x, тыс. руб.):

i	1	2	3	4	5	6	7	8	9	10
x	2,8	2,4	2,1	2,6	1,7	2,5	2,4	2,6	2,8	2,6
y	28,0	21,3	21,0	23,3	15,8	21,9	20,0	22,0	23,9	26,0

         

21. По территориям некоторых регионов (i – номер региона) известны данные за год по среднедневной заработной плате (y, руб.) и среднедушевому прожиточному минимуму в день одного трудоспособного (x, руб.):

i	1	2	3	4	5	6	7	8	9	10
x	91	90	112	104	97	121	96	114	97	106
y	130	122	145	134	137	152	141	144	124	132

     

22. По 13 регионам страны изучается зависимость среднемесячной заработной платы (y, тыс. руб.) от инвестиций в основной капитал на душу населения (x, тыс. руб.):

i	1	2	3	4	5	6	7	8	9	10	11	12	13
x	4,9	8,5	9,1	5,5	6,1	5,1	4,2	3,8	11	6,9	7,5	5,5	5,8
y	3,9	5,5	4,8	4	3,9	3,8	4,1	3	6,3	4,8	5,2	3,7	3,5

       

23. По 13 регионам страны изучается зависимость розничной продажи телевизоров (y, шт.) от среднедушевых денежных доходов в месяц                     (x, тыс. руб.):

i	1	2	3	4	5	6	7	8	9	10	11	12	13
x	2,4	3	2,2	2,1	4	2,5	5	2,3	3	3,4	3,9	2,3	3,1
y	4,8	5,7	5,1	5,5	6,2	4,9	7	4,7	4,9	5,5	5,6	4,4	5,8

       

24. По территориям некоторых регионов (i – номер региона) известны данные за год по среднедневной заработной плате (y, руб.) и среднедушевому прожиточному минимуму в день одного трудоспособного (x, руб.):

i	1	2	3	4	5	6	7	8	9	10
x	89	87	113	108	100	119	97	115	97	106
y	137	128	156	148	149	162	152	156	134	142

         

25. Изучается зависимость материалоемкости продукции от размера предприятия по 10 однородным заводам:

Выпуск продукции, тыс. ед., x	100	200	300	400	500	600	700	150	120	250
Потреблено материалов на единицу продукции, кг, y	9	6	5	4	3,7	3,6	3,5	6	7	3,5

  

26. По 10 регионам страны изучается зависимость среднемесячной заработной платы (y, тыс. руб.) от инвестиций в основной капитал на душу населения (x, тыс. руб.):

i	1	2	3	4	5	6	7	8	9	10
x	3,8	11	6,9	7,5	5,5	5,8	5	6	10	9
y	3	6,3	4,8	5,2	3,7	3,5	4,2	4,5	6,6	6,7

         

27. По 12 регионам страны изучается зависимость средней заработной платы (y, тыс. руб.) от валового регионального продукта на душу населения (x, тыс. руб.):

i	1	2	3	4	5	6	7	8	9	10	11	12
x	35,8	22,5	28,3	26	20	31,8	30,5	29,5	41,5	41,3	34,5	34,9
y	3,5	2,6	3,2	2,6	2,6	3,5	3,1	2,9	3,4	4,8	3	3,1

       

28. По 12 регионам страны изучается зависимость розничной продажи телевизоров (y, шт.) от среднедушевых денежных доходов в месяц                    (x, тыс. руб.):

i	1	2	3	4	5	6	7	8	9	10	11	12
x	2,6	2,5	2,9	2,6	2,2	2,6	3,3	3,9	4	3,7	3,4	2,6
y	24,6	21	27	21	24	24	31,9	33	35,4	34	31	26

 

29. По 13 регионам страны изучается зависимость ожидаемой продолжительности жизни при рождении (y, лет) от уровня заболеваемости детей в возрасте 0–14 лет на тысячу человек (x):

i	1	2	3	4	5	6	7	8	9	10	11	12	13
x	1516,3	1474,3	1390,5	2208,7	982,7	1520,5	1809,5	1569,4	1654,2	1749,5	1746,0	1475,1	1753,4
y	64	66	67,8	62,1	68,1	63,7	64	65,4	65,7	62,3	65,6	65,6	65,3

 

30. По 12 регионам страны изучается зависимость средней заработной платы (y, тыс. руб.) от валового регионального продукта на душу населения (x, тыс. руб.):

i	1	2	3	4	5	6	7	8	9	10	11	12
x	41,5	41,3	34,5	34,9	34,7	26,8	32,5	32,4	50,9	44,8	79,1	47,4
y	3,4	4,8	3	3,1	3,3	2,6	3,3	3,3	3,9	4,7	6,5	5

 

31. По территориям 10 регионов (i – номер региона) известны данные за год по среднедневной заработной плате (y, руб.) и среднедушевому прожиточному минимуму в день одного трудоспособного (x, руб.):

i	1	2	3	4	5	6	7	8	9	10
x	99	97	120	115	110	130	107	125	107	99
y	147	138	164	157	160	175	163	168	145	154

         

32. По 10 регионам страны изучается зависимость средней заработной платы (y, тыс. руб.) от валового регионального продукта на душу населения (x, тыс. руб.):

i	1	2	3	4	5	6	7	8	9	10
x	59,3	26,2	38,9	61,1	48,4	33,1	53,3	47,4	79,1	44,8
y	5,4	2,9	3,4	7,2	4,5	3,7	4,5	5	6,5	4,7

        

 

 

33. По территориям 10 регионов (i – номер региона) известны данные за год по среднедневной заработной плате (y, руб.) и среднедушевому прожиточному минимуму в день одного трудоспособного (x, руб.):

i	1	2	3	4	5	6	7	8	9	10
x	69	87	112	95	88	105	100	100	101	88
y	118	130	159	138	140	152	158	145	141	127

       

34. Для 10 однотипных предприятий (i – номер предприятия) имеются данные за год о производительности труда (y, т/ч) и уровне механизации работ (x, %):

i	1	2	3	4	5	6	7	8	9	10
x	32	30	36	40	41	47	56	54	60	55
y	20	24	28	30	31	33	34	37	38	40

 

35. По территориям 10 регионов (i – номер региона) известны данные за год по среднедневной заработной плате (y, руб.) и среднедушевому прожиточному минимуму в день одного трудоспособного (x, руб.):

i	1	2	3	4	5	6	7	8	9	10
x	67	65	82	77	90	87	88	61	69	79
y	117	108	125	118	137	130	141	107	108	116

    

Приложение 1

Таблица значений F-критерия Фишера при уровне значимости α=0.05

                                                                             k₁

 k₂      1 2  3  4  5  6  7  8  9 10 15

1     161.45 199.50 215.71 224.58 230.16 233.99 236.77 238.88 240.54 241.88 245.95

2     18.51 19.00 19.16 19.25 19.30 19.33 19.35 19.37 19.38 19.40 19.43

3     10.13 9.55 9.28 9.12 9.01 8.94 8.89 8.85 8.81 8.79 8.70

4     7.71 6.94 6.59 6.39 6.26 6.16 6.09 6.04 6.00 5.96 5.86

5     6.61 5.79 5.41 5.19 5.05 4.95 4.88 4.82 4.77 4.74 4.62

6     5.99 5.14 4.76 4.53 4.39 4.28 4.21 4.15 4.10 4.06 3.94

7     5.59 4.74 4.35 4.12 3.97 3.87 3.79 3.73 3.68 3.64 3.51

8     5.32 4.46 4.07 3.84 3.69 3.58 3.50 3.44 3.39 3.35 3.22

9     5.12 4.26 3.86 3.63 3.48 3.37 3.29 3.23 3.18 3.14 3.01

10   4.96 4.10 3.71 3.48 3.33 3.22 3.14 3.07 3.02 2.98 2.85

11   4.84 3.98 3.59 3.36 3.20 3.09 3.01 2.95 2.90 2.85 2.72

12   4.75 3.89 3.49 3.26 3.11 3.00 2.91 2.85 2.80 2.75 2.62

13   4.67 3.81 3.41 3.18 3.03 2.92 2.83 2.77 2.71 2.67 2.53

14   4.60 3.74 3.34 3.11 2.96 2.85 2.76 2.70 2.65 2.60 2.46

15   4.54 3.68 3.29 3.06 2.90 2.79 2.71 2.64 2.59 2.54 2.40

16   4.49 3.63 3.24 3.01 2.85 2.74 2.66 2.59 2.54 2.49 2.35

17   4.45 3.59 3.20 2.96 2.81 2.70 2.61 2.55 2.49 2.45 2.31

18   4.41 3.55 3.16 2.93 2.77 2.66 2.58 2.51 2.46 2.41 2.27

19   4.38 3.52 3.13 2.90 2.74 2.63 2.54 2.48 2.42 2.38 2.23

20   4.35 3.49 3.10 2.87 2.71 2.60 2.51 2.45 2.39 2.35 2.20

 

 

---

Дата добавления: 2018-06-01; просмотров: 3540; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!