Кинетическая энергия вращающегося тела

Центр масс, центр ине́рции, барице́нтр (от др.-греч. βαρύς — тяжёлый + κέντρον — центр) — (в механике) геометрическая точка, характеризующая движение тела или системы частиц как целого[1]. Не является тождественным понятию центра тяжести(хотя чаще всего совпадает). В динамике широко используется понятие центра масс системы материальных то чек, который обычно обозначают буквой С. Положение центра масс определяется радиусом-вектором . (8) Здесь mi – масса i-той материальной точки, – радиус-вектор, задающий положение этой точки, – суммарная масса системы. Отметим, что в однородном поле сил тяжести центр масс совпадает с центром тяжести системы. Скорость центра масс , (9) где – импульс системы. Согласно (9) импульс системы . (10) Подставив (10) в (6), получим уравнение движения центра масс . (11) Таким образом, центр масс движется так, как двигалась бы материальная точка с массой, равной массе системы, под действием результирующей всех внешних сил, приложенных к телам системы. Для замкнутой системы и, следовательно, [см. (11)] ,(12) это означает, что центр масс замкнутой системы движется прямолинейно и равномерно, либо покоится. Система отсчета, относительно которой центр масс покоится, называется системой центра масс. Эта система инерциальна. Дифференциальные уравнения движения системы Рассмотрим систему, состоящую из n материальных точек. Выделим какую-нибудь точку системы с массой mk. Обозначим равнодействующую всех приложенных к точке внешних сил (и активных, и реакций связей) через F¯ke, а равнодействующую всех внутренних сил -- через F¯kl. Если точка имеет при этом ускорение ak¯, то по основному закону динамики: Аналогичный результат получим для любой точки. Следовательно, для всей системы будет: Уравнения (1) представляют собой дифференциальные уравнения движения системы в векторной форме. Проектируя равенства (1) на координатные оси, получим уравнения движения системы в дифференциальной форме в проекциях на эти оси. Однако при решении многих конкретных задач необходимость находить закон движения каждой из точек системы не возникает, а бывает достаточно найти характеристики, определяющие движение всей системы в целом. Теорема о движении центра масс системы Для определения характера движения системы требуется знать закон движения ее центра масс. Центром масс или центром инерции системы называется такая воображаемая точка, радиус-вектор Rкоторой выражается через радиус векторы r1,r2,...материальных точек по формуле: R=m1r1+m2r2+...+mnrnm, (2) где m=m1+m2+...+mn - общая масса всей системы. Чтобы найти этот закон, обратимся к уравнениям движения системы (1) и сложим почленно их левые и правые части. Тогда получим: ∑mka¯k=∑F¯ke+∑F¯kl. (3) Из формулы (2) имеем: Беря вторую производную по времени, получаем: ∑mka¯k=Ma¯c, (4) где a¯c- ускорение центра масс системы. Так как по свойству внутренних сил в системе ∑F¯kl=0, получим окончательно из равенства (3), учтя (4): Ma¯c=∑F¯ke. (5) Уравнение (5) выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил или центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему. Проецируя обе части равенства (5) на координатные оси, получим: Mx¨c=∑F¯kxe, My¨c=∑F¯kye, Mz¨c=∑F¯kze. (6) Эти уравнения представляют собой дифференциальные уравнения движения центра масс в проекциях на оси декартовой системы координат. Теорема Поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе тела. В остальных случаях тело можно рассматривать как материальную точку лишь тогда, когда практически для определения положения тела достаточно знать положение его центра масс и допустимо по условиям задачи не принимать во внимание вращательную часть движения тела; Теорема позволяет исключать из рассмотрения все наперед неизвестные внутренние силы. В этом ее практическая ценность. ТЕОРЕМА При движении системы материальных точек ее центр масс движется так, как двигалась бы материальная точка, помещенная в центре масс, если бы в ней были сконцентрированы массы всех точек системы и к ней были бы приложены все внешние силы, действующие на точки системы: внRвн→=M⋅ac→, где внRвн→ − векторная сумма всех внешних сил, M − масса системы материальных точек, ac→ − ускорение центра масс системы материальных точек. Моме́нтине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения в Международной системе единиц (СИ): кг·м². Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения. Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Кинетическая энергия вращающегося тела

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:

Если тело вращается вокруг неподвижной оси с угловой скоростью , то линейная скорость i-ой точки равна , где 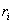, - расстояние от этой точки до оси вращения. Следовательно.

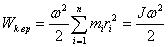
(5.11)

где 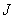- момент инерции тела относительно оси вращения.

В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости центра инерции тела, и вращения с угловой скоростью вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

(5.12)

где - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.

Кинетическая энергия – величина аддитивная. Поэтому кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек, на которые это тело можно мысленно разбить:

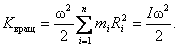(6.4.1)

Если тело вращается вокруг неподвижной оси z с угловой скоростью , то линейная скорость i-й точки , R_i – расстояние до оси вращения. Следовательно,

(6.4.2)

Сопоставив (6.4.1) и (6.4.2), можно увидеть, что момент инерции тела I является мерой инертности при вращательном движении, так же как масса m – мера инерции при поступательном движении.
В общем случае движение твердого тела можно представить в виде суммы двух движений – поступательного со скоростью v_c и вращательного с угловой скоростью ω вокруг мгновенной оси, проходящей через центр инерции. Тогда полная кинетическая энергия этого тела

(6.4.3)

Здесь I_c – момент инерции относительно мгновенной оси вращения, проходящей через центр инерции.

Дата добавления: 2018-06-01; просмотров: 651; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!