Реализация решения задачи оптимизации режима ЭЭС
С использованием математического пакета MathCAD
 |
Рассмотрим упрощенную задачу определения оптимальной нагрузки электростанций (ЭС) для энергосистемы, представленной на рис. 1.15.
Рис. 1.15. Схема энергосистемы.
Пренебрегаем потерями активной мощности в сетях. Распределению подлежит активная нагрузка, равная 
. Все ЭС тепловые.
Расходные характеристики энергоблоков каждой ТЭС представим в виде квадратичного полинома:
,
где 
– часовые затраты i-го энергоблока ТЭС в зависимости от его активной мощности 
;
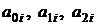– коэффициенты квадратичного полинома.
Эквивалентная расходная характеристика j-ой ТЭС, сформированная с учетом характеристик энергоблоков, имеет вид:
.
Если принять 
, то суммарные часовые затраты на j-ой ТЭС будут равны:
,
где 
– установленная мощность электростанции j;
m – число энергоблоков на j-й ТЭС.
Тогда с учетом того, что 
, имеем:
;
;
.
Допустим, что матрица номинальных мощностей (МВт) энергоблоков ТЭС такова (нижняя граница индексации принимается равной единице ORIGIN:=1):
,
где по столбцам заданы номинальные мощности каждого i-го (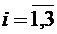 
) энергоблока j-ой ( 
) ТЭС.
Матрицы коэффициентов 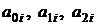характеризуем следующими численными реализациями:
По столбцам каждой из матриц коэффициентов записаны значения соответствующих коэффициентов тех энергоблоков, мощности которых заданы в матрице 
.
Расчет коэффициентов квадратичного полинома 
эквивалентной расходной характеристики применительно к численным значениям данной задачи:
‑ вектор установленных мощностей ЭС1, ЭС2 и ЭС3, МВт;
‑ активная нагрузка, МВт.
Имеем
Определение мощностей ТЭС, соответствующей точке экономического режима, 
определяется из условия равенства 
(см. рис. 7.2). Воспользовавшись этим условием, имеем:
.
Отсюда:
Для численных значений данной задачи имеем ЭС1, ЭС2 и ЭС3, МВт:
Для нахождения оптимальных нагрузок ТЭС воспользуемся принципом равенства удельных приростов затрат и балансом активных мощностей. Примем в качестве балансирующей ЭС3.
Решение в общем виде можно получить в соответствии с отмеченным выше из системы уравнений:
,
которую можно преобразить к такому виду:
.
Отсюда
или
.
Окончательно
Применительно к численным значениям данной задачи (ЭС3 – балансирующая) имеем матрицу Р активных мощностей ЭС1 иЭС2, МВт:
Проверка ограничения (1.31) при решении задачи оптимизации показывает, что ЭС1 и ЭС2 работают в экономичном режиме. Действительно:
;
.
По этому алгоритму решается и задача оптимизации распределения активной мощности между энергоблоками ТЭС. В частности, когда активная мощность ТЭС оказывается меньше мощности, соответствующей точке экономического режима (в данной задаче 
), можно разгрузить один из блоков данной ТЭС, т.е. принять его мощность 
, и по рассмотренному алгоритму распределить активную мощность 
между оставшимися в работе энергоблоками с учетом их номинальных мощностей.
Дата добавления: 2018-05-31; просмотров: 419; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!