Решение: A-книга есть в библиотеке, B – книга не выдана.
Из 20 вопросов, входящих в экзаменационный билет, студент подготовил 17. Найти вероятность того, что студент ответил правильно на экзаменационный билет, состоящий из 2-х вопросов.
Решение: Cmn = n! / m!(n-m)!
C220 = 20! / 2! (20-2)! = 18! * 19 * 20 / 18! * 2! = 190 –общее число случаев
C217 = 17! / 2! (17-2)! = 15! * 16 * 17 / 2! * 15! = 136 – общее число благоприятных случаев.
P(A) = 136 / 190 = 0, 7157
Ответ: 0,7157
2. Рабочий обслуживает 3 станка. Вероятность безотказной работы первого из них равна 0,75, второго 0,85,
третьего 0,95. Найти вероятность того, что а) откажут два станка, б) все три станка будут работать безотказно,в) хотя бы один станок откажет в работе.
3. Из колоды содержащей 52 карты вынимается наугад 3. Найти вероятность того, что это тройка, семёрка и туз.
4. Найти вероятность того, что абонемент наберет правильный двухзначный номер, если он знает, что данный номер не делится на 5
Решение:P(A) = m/n; m=1/
Посчитаем общее количество двухзначных чисел. Оно равно 90 и вычтем из этих чисел те которые делятся на 5 (10,15,20,25…90,95). Их количество равно 18 => n=90-18=72
P= 1/72
Ответ: 1/72
Игральная кость подброшена 2 раза: а) Найти вероятность того, что сумма очков на верхних гранях составит 7.б)найти вероятность того, что хотя бы 2 очка появится при одном подбрасывание.
Решение:P(A)=m/n
n=6*6=36; m=6.
а) P(A)=6/36 =1/6
б) P(B)=1-5/6*5/6=1-25/36 =11/36
В урне имеется 5 черных и 7 красных шаров. Последовательно (без возвращения) извлекается три шара. Найти вероятность того, что а)все три шара будут красными, б)три шара красными или черными.
|
|
|
Решение:Cmn = n! / m!(n-m)!
C312 = 220 - вариантов вытащить три шара.
а) Вытащить 3 красных из 7 можно C37 способами.
m = C37 = 7! / 3!*4! = 35
P (A1) = m/n = 35/220 = 7/44
б) вытащить 3 красных из 7 можно C37 способами, и 3 черных из 5 =>
С35 способами.
m = C37 + С35 = 35 + 5! / 3!*2! = 35 + 10 = 45
P(A2) = m/n = 45/220 = 9/44
Ответ: а) P(A) = 7/44 ; б) P (A2) = 9/44
В группе из 15 человек 6 человек занимаются спортом. Найти вероятность того, что из случайно отобранных 7 человек 5 человек занимаются спортом.
Решение:P(A) = C56 * C29 / C715 = ((6!/(5!*1!))*(9!/(2!*7!)) / (15! / (7!*8!) = (5*36) / (15* 14* 13* 12* 11* 10* 9* 8!) / (1*2*3*4*5*6*7*8) = (5*36*12) / (15*13*11*3) = 4/143 =0,03
Ответ: 0,3.
Мышь может выбрать наугад один из 5 лабиринтов. Известно, что вероятность ее выхода из различных лабиринтов за 3 минута равны 0,5; 0,6; 0,2; 0,1; 0,1. Пусть оказалось, что мышь выбралась из лабиринта за 3 минуты. Какова вероятность того, что она выбрала первый лабиринт? Второй лабиринт?
Решение: Изначально вероятности выбора лабиринта мышью равны:
P(H1) = P(H2) = P(H3) = P(H4) = P(H5) = 1/5 – вероятность выбора 1,2,3,4,5 лабиринт соответственно.
A – выход из лабиринта.
P(A/H1) = 0,5 – Вероятность выхода мыши из 1 лабиринта
P(A/H2) = 0,6 – из 2 лабиринта.
P(A/H3) =0,2 –из 3 лабиринта
|
|
|
P(A/H4) = 0,1 –из 4 лабиринта
P(A/H5) = 0,1 – из 5 лабиринта
По формуле полной вероятности:
P(A) = ∑ P(Hi)P(A/Hi) = P(H1)P(A/H1) + P(H2)P(A/H2) +P(H3)P(A/H3) +P(H4)P(A/H4) +P(H5)P(A/H5)
P(A) = 1/5*0,5 + 1/5*0,6 + 1/5*0,2 + 1/5*0,1 +1/5*0,1 = 1/5 (0,5+0,6+0,2+0,1+0,1)=1/5*1,5=1,5*3/2 = 3/10 –вероятность выхода мыши из лабиринта за 3 минуты.
А)Найдем вероятность того,что мышь выбрала первый лабиринт(по формуле Бэйеса):
P(H1/A) = P(H1)P(A/H1) / P(A) = (0,5*1/5)/(3/10) = (1/2*1/5) /(3/10) = 1/10*10/3 = 1/3
P(H1/A) = 1/3
Б) Найдем вероятность того,что мышь выбрала второй лабиринт(по формуле Бэйеса)
P(H2/A) = P(H2)P(A/H2) / P(A) = (1/5*0,6) / 3/10 = (1/5*3/5) / 3/10 = 3/25* 10/3 = 10/25 = 2/5
Ответ: 1/3; 2/5
9. Из 10 билетов выигрышными являются 2. Найти вероятность того, что из 5 билетов выигрышным является один.
10. В сентябре вероятность дождливого дня 0,3. Команда «Статистик» выигрывает в ясный день с вероятностью 0,8, а в дождливый день эта вероятность равна 0,3. Известно, что в сентябре они выиграли некоторую игру.Какова вероятность, что в тот день: а) шел дождь; б) был ясный день.
11. Вероятность попадания в цель первым стрелком равна 0,7, вторым - 0,5, третьим -0,4. Найти вероятность того, что хотя бы один стрелок попадет в цель.
Решение:
В первом ящике содержится 20 деталей, из них 10 стандартных, во втором 30 деталей, из них 25 стандартных, в третьем 10 деталей, из них 8 стандартных. Из случайно взятого ящика наудачу взята одна деталь, которая оказалась стандартной. Найти вероятность того, что она взята из второго ящика.
|
|
|
Решение: P(Hi) = 1/3; P(A/H1)=10/20=1/2; P(A/H2)=25/30=5/6;
P(A/H3)=8/10=4/5;
P(A)=1/3(1/2+5/6+4/5) = 62/45
P(H2/A) = (P(H2)*P(A/H2)) / P(A) = (1/3*5/6) /62/45 = 0,39
13. На каждой из пяти одинаковых карточек написана одна из следующих букв: А, Е, Н, С, Т. Карточки
перемешаны. Определить вероятность того, что из вынутых и положенных в ряд карточек а) можно составить
слово «СТЕНА», б) из трех карточек можно составить слово «НЕТ».
Для поражения цели достаточно попадания хотя бы одного снаряда. Произведено два залпа из двух орудий. Найти вероятность поражения цели, если вероятность попадания в цель при одном выстреле из первого орудия равна 0,46, второго 0,6.
Решение:
Пусть B ни одного попадания
A1 – попадания при 1-ом выстреле.
А2 – попадание при 2-ом выстреле.
P(B) = --А1—А2 = 0,54* 0,4 = 0,216
Тогда С - хотя бы одно попадание.
P(C)= 1 - 0,216 = 0,784
Ответ: 0,784
Имеется 3 урны. В первой урне 6 черных и 4 белых, во второй 5 белых и 5 черных, в третьей 7 белых и 3 черных. Случайно выбирается урна и из нее извлекается шар, который оказался белым. Найти вероятность того, что выбрана вторая урна.
|
|
|
Решение:
H1=1/3; H2=1/3; H3=1/3
P(H/H1) = 4/10; P(H/H2) = 1/2; P(H/H3) = 7/10
P(H) = 1/3*4/10 + 1/3*1/2 + 1/3*1/7 = 16/30
P(H2/H) = (1/2*1/3)/ (8/15) = 1/6* 15/8 = 15/48
Ответ: 15/48 = 0,3125
16. Монета подбрасывается 3 раза. Найти вероятность того, что герб появится: а) все 3 раза, б) только один раз, в)хотя бы один раз
Решение:
17. На отдельных карточках написаны цифры 0, 1,2, 3, 4, 5, 6, 7, 8, 9. Все карточки перемешиваются, после чего наугад берут 5 карточек и раскладывают их в ряд. Определить вероятность того, что будет получено число 1 2 0 3 5. (Задачу решить, используя определение вероятности события и теоремы теории вероятностей)
Три известных экономиста одновременно предложили свои теории, которые считались равновероятными. После наблюдения над состоянием экономики оказалось, что вероятность того развития, которое она получила на самом деле в соответствии с первой теорией равна 0,5; со второй – 0,7; с третьей – 0,4. Каким образом это изменят вероятности правильности трех теорий.
Решение:
P(A/H1)=0,5; P(A/H2)=0,7; P(A/H3)=0,4
P(A)=P(H1)*P(A/H1)+…=1/3*0,5+1/3*0,7+
1/3*0,4=1/3(0,5+0,7+0,4)=1,6/3=0,533
P(H1/A)=(1/3*0,5)/(1/3*1,6)=0,5/1,6=0,32.
P(H2/A)=0,7/1,6=0,42
P(H3/A)=0,25
В Магазине продается 4 магнитофона. Вероятность того, что они выдержат гарантийный срок, соответственно равны: 0,91; 0,9; 0,95; 0,94. Найти вероятность того, что взятый найдачу магнитофон выдержит гарантийный срок.
Решение:Вероятность покупки 1магнитофон –1/4 ; 2 – 1/4; 3 – 1/4 ; 4 –1/4.
P(A) = 1/4 * 0,91 + ¼ * 0,9 + ¼ * 0,95 + ¼ * 0,94 = 0,2275 + 0,225 + 0,2375 + 0,235 = 0,925
Ответ: P(A) = 0,925
Игральная кость сделана так, что вероятность выпадения определенного числа пропорциональна числу очков. Какова вероятность выпадения трех очков, если известно, что выпало нечетное число очков.
1 2 3 4 5 6
P x 2x 3x 4x 5x 6x
P(1)+P(2)+P(3)+P(4)+P(5)+P(6)=1
x+2x+3x+4x+5x+6x=1
21x=1
X=1/21
x 3x 5x
P(1)+P(3)+P(5)=1/21+3/21+5/21 = 9/21=3/7 –вероятность выпадения нечетного числа очков.
3x/9x=1/3
P=m/n=3x/9x=1/3
21. Брошены 2 игральные кости. Какова вероятность того, что абсолютная величина разности выпавших очков равна 3?
Студент в поисках книги посещает 3 библиотеки. Вероятность того, что они есть в библиотеке равны 0,4; 0,5; 0,1; а того, что они выданы или нет – равновероятные события. Какова вероятность того, что нужна книга найдена.
Решение: A-книга есть в библиотеке, B – книга не выдана.
P(B) = P(B-) = ½
P(A1) = 0,4 P(A2) = 0,5 P(A3) = 0,1
Определим вероятность того, что нужная книга найдена:
P = P(A1)* P(B) + P(A2)*P(B) + P(A3)*P(B) = P(B)(P(A1) + P(A2) + P(A3) = 1/2 * (0,4 + 0,5 +0,1) = 1/2 * 1 = ½
Ответ: 1/2
23. Найти вероятности того, что дни рождения 12 человек прийдутся на разные месяцы года.
Решение: P(A)= m/n
m = P12 = 12!
n = ---A12= 1212
P = 12! / 1212 = 11! / 1211 = (11*10*9*8*7*6*5*4*3*2*1) / (12*12*12*12*127) = (11*5*7*5*1) / 127 = 7*8*25 / 127 = 1925 / 127
Ответ: 1925/127
24. В урне имеется 10 белых, 5 черных и 15 красных шаров. Извлекается последовательно 2 шара. Рассматриваются 2 события А - хотя бы один шар из двух вынутых красный, В - хотя бы один вынутый шар белый. Найти вероятность события С = А + В.
25.Наудачу набранный номер состоит из 5 цифр. Определить вероятность того, что все цифры в нем различны.
26.В магазин трикотажных изделий поступили носки, 60% которых получено от одной фабрики, 25% - другой и 15% - третьей. Найти вероятность того, что купленные покупателем носки изготовлены на второй или третьей фабрике.
Решение. A1-от 1 фабрики, P(A1) = 0,6;
А2 –от 2 фабрики; P(A2) = 0,25
A3 – от 3 фабрики; P(A3) = 0,15
P(A2+A3) = 0,25 + 0,15 = 0,4
Ответ: 0,4
Пассажир за получением билета может обратиться в одну из касс. Вероятность обращения в 1ую кассу составляет 0,4; во 2ую 0,35; и 3ью 0,25. Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут проданы, равна для 1ой кассы 0,3; для 2ой 0,4, для 3ей 0,6. Найти вероятность того, что пассажир купит билет.
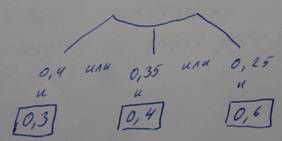P(A) –вероятность не купить билет.
P(A) =0,4*0,3 + 0,35*0,4 + 0,25*0,6 =
0,12 + 0,14 + 0,15 = 0,41
P(A1) – вероятность купить билет = 1-P(A) = 1 – 0,41 = 0,59.
Ответ: P(A1) = 0,59.
28. Бросаются 4 игральные кости. Найти вероятность того, что: а) хотя бы на одной появится 2 очка, б) на них выпадет по одинаковому числу очков.
Решение: 
29. Из 9 жетонов, занумерованных разными однозначными цифрами, выбирается 3. Найти вероятность того, что последовательная запись их номеров покажет возрастание значений цифр.
Решение:
30. Вероятность выигрыша по лотерейному билету равна 0,1. Какова вероятность того, что выиграет хотя бы один билет из трех купленных?
Дата добавления: 2018-05-31; просмотров: 2228; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!