Дифракция света на одной щели при нормальном падении лучей.
Министерство образования и науки Российской Федерации
Архангельский государственный технический университет
ОПТИКА
Методические указания к выполнению контрольного задания № 4
по курсу общей физики для студентов заочного факультета
инженерно-технических специальностей
Архангельск
2005
Рассмотрены и рекомендованы к изданию методической
комиссией факультета промышленной энергетики
Архангельского технического университета
26 мая 2004 г.
Составители:
Л.В. Филимоненкова, доц. канд. техн. наук
Рецензент
А.В.Соловьев, доцент кафедры биомедицинской техники, канд. тех. наук
УДК 533.1
Филимоненкова Л.В., Оптика: Методические указания к выполнению контрольного задания № 4 для студентов – заочников инженерно – технических специальностей. Архангельск: Изд-во АГТУ, 2004. – 42 с.
Подготовлены кафедрой физики АГТУ.
В указаниях излагаются основные законы и формулы по разделу «Оптика», приведены примеры решения задач.
Предназначены для студентов-заочников инженерно-технических специальностей.
Ил. 11. Табл. 2.
© Архангельский государственный
технический университет, 2004
РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
К выполнению контрольной работы следует приступить только после изучения материала, соответствующего данному разделу программы, внимательного ознакомления с примерами решения задач, приведенных в данном пособии по каждому разделу курса.
|
|
|
При выполнении контрольной работы необходимо руководствоваться следующими правилами.
1. Контрольная работа выполняется в обычной школьной тетради (каждая контрольная выполняется в отдельной тетради). Для замечаний рецензента на страницах тетради оставляются поля. Каждая следующая задача должна начинаться с новой страницы. Условия задач переписываются полностью без сокращений.
2. При решении задач следует пользоваться международной системой единиц (СИ). Все величины, входящие в условия задачи, выражаются в единицах этой системы.
3. Решения задач должны сопровождаться краткими, но исчерпывающими пояснениями, раскрывающими физический смысл употребляемых формул. В тех случаях, когда это возможно, дать чертеж, выполненный с помощью чертежных принадлежностей.
Если при решении задачи применяется формула, получаемая для частного случая, не выражающая какой-нибудь физический закон или не являющаяся определением какой-нибудь физической величины, то её следует вывести.
4. Решать задачу надо в общем виде, то есть выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин.
|
|
|
Получив решение в общем виде, сделать анализ его размерности. Для этого надо подставить в правую часть полученной рабочей формулы вместо символов величин обозначения единиц, провести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине. Если такого соответствия нет, то это означает, что задача решена неверно.
5. В конце контрольной работы следует указать учебники и учебные пособия, которыми пользовались при решении задач.
6. Получив из университета проверенную работу, следует внимательно ознакомиться с замечаниями и указаниями рецензента. Если при выполнении контрольной работы были допущены ошибки, необходимо выполнить работу над ошибками в той же тетради и направить ее на повторную проверку.
7. После получения положительной рецензии студент обязан пройти собеседование по существу решенных задач. Итогом собеседования является зачет по контрольной работе.
Студентам, проживающим вблизи университета или филиалов и учебно–консультационных пунктов, рекомендуется прослушать курс лекции по физике, организуемых для студентов заочников, а также использовать очные консультации преподавателей кафедры физики.
|
|
|
Колебания и волны
1.1 Механические гармонические колебания.
· Уравнение гармонических колебаний и его решение:

 *,
*,
где х – значение колеблющейся величины в момент времени t; А – амплитуда колебаний (максимальное значение колеблющейся величины);  – фаза колебаний в момент времени t;
– фаза колебаний в момент времени t;  – начальная фаза в момент времени t=0; ω0 – собственная циклическая частота колебаний.
– начальная фаза в момент времени t=0; ω0 – собственная циклическая частота колебаний.
· Период гармонических колебаний:
 ;
;  ,
,
где ν – частота колебаний (число полных колебаний в единицу времени).
· Скорость точки, совершающей колебания:

· Ускорение точки, совершающей колебания:
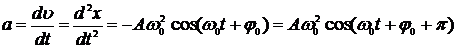 .
.
Амплитуда скорости и ускорения соответственно равны  и
и  . Фаза скорости отличается от фазы смещения на
. Фаза скорости отличается от фазы смещения на  , а фаза ускорения на
, а фаза ускорения на  .
.
· Сила, под действием которой точка массой m совершает колебания:
 ,
,
где  – коэффициент упругости,
– коэффициент упругости,  .
.
· Кинетическая энергия материальной точки, совершающей гармонические колебания:
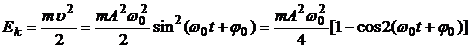 .
.

* В пособии используется функция косинуса.
· Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F:
|
|
|


· Полная энергия:
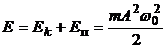 .
.
На Рис.1 изображены графики зависимости энергий от времени. Энергии  изменяются с частотой 2ω0 , т.е. с частотой, которая в 2 раза превышает частоту изменения х от времени.
изменяются с частотой 2ω0 , т.е. с частотой, которая в 2 раза превышает частоту изменения х от времени.
Рис.1
1.2 Гармонические осцилляторы: пружинный, физический и математический маятники, колебательный контур (системы, совершающие гармонические колебания).
· Период колебаний пружинного маятника:
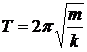 ,
,
где m – масса тела, подвешенного на пружине; k – жесткость пружины.
· Период колебаний математического маятника:
 ,
,
где l – длина маятника, g – ускорение свободного падения.
· Период колебаний физического маятника:
 =
=  ,
,
где I – момент инерции маятника относительно оси колебаний; m – масса маятника; d – расстояние от центра масс маятника до оси колебаний;  - приведенная длина физического маятника.
- приведенная длина физического маятника.
1.3 Сложение гармонических колебаний.
· При сложении двух одинаково направленных гармонических колебаний одинаковой частоты получается гармоническое колебание той же частоты с амплитудой:
 ;
;
и с начальной фазой, определяемой из уравнения:
 ,
,
 где А1, А2 – амплитуды составляющих колебаний;
где А1, А2 – амплитуды составляющих колебаний;  ,
,  – их начальные фазы.
– их начальные фазы.
При сложении колебаний:  используют метод вращающего вектора амплитуды, рис.2.
используют метод вращающего вектора амплитуды, рис.2.
· При сложении двух взаимно перпендикулярных колебаний одинаковой частоты с амплитудами А1 и А2 и начальными Рис.2
фазами  ,
,  уравнение траектории результирующего движения в координатах x, y имеет вид:
уравнение траектории результирующего движения в координатах x, y имеет вид:
 .
.
1.4 Затухающие колебания.
· Уравнение затухающих колебаний и его решение:
 ,
,  ,
,
где А(t)=  – амплитуда затухающих колебаний; А0 – амплитуда колебаний в момент t=0; δ – коэффициент затухания (
– амплитуда затухающих колебаний; А0 – амплитуда колебаний в момент t=0; δ – коэффициент затухания (  ); r – коэффициент сопротивления;
); r – коэффициент сопротивления;  – циклическая частота затухающих колебаний; ω0 – собственная циклическая частота свободных незатухающих колебаний той же колебательной системы.
– циклическая частота затухающих колебаний; ω0 – собственная циклическая частота свободных незатухающих колебаний той же колебательной системы.
· Время релаксации:
 ,
,
где τ – промежуток времени, в течение которого амплитуда затухающих колебаний уменьшится в е раз (е – основание натурального логарифма).
· Логарифмический декремент затухания λ:
 ,
,
где A(t), A(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающихся на период; N – число колебаний, совершаемых за время уменьшения амплитуды в е раз.
1.5 Вынужденные колебания.
· Уравнение вынужденных колебаний и его установившееся решение:
 ;
;  ,
,
где  – внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая колебания; ω – циклическая частота изменения внешней вынуждающей силы.
– внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая колебания; ω – циклическая частота изменения внешней вынуждающей силы.
· Амплитуда вынужденных колебаний:
 .
.
· Резонанская частота и резонанская амплитуда:
 ,
,  .
.
1.6 Электромагнитные колебания.
· Уравнение свободных колебаний в идеальном колебательном контуре и его решение:
 ,
, 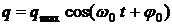 ,
,
где q – заряд на обкладках конденсатора в момент времени t; qmax – амплитуда колебаний заряда конденсатора с циклической частотой конденсатора ω0, называемой собственной частотой контура:
 ,
, 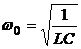
и периодом:
 - формула Томсона,
- формула Томсона,
где С – емкость конденсатора, L – индуктивность катушки, составляющих колебательный контур.
· Полная энергия идеального колебательного контура:

или
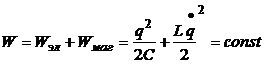 ,
,
где С – емкость конденсатора, L – индуктивность катушки, составляющих колебательный контур.
В контуре возникают электрические колебания, сопровождающиеся превращениями энергий электрического  и магнитного
и магнитного  полей.
полей.
1.7 Свободные затухающие колебания в электрическом колебательном контуре.
· Уравнение затухающих колебаний в контуре и его решение:

 ,
,
где  – величина заряда на пластинах конденсатора в момент времени t=0;
– величина заряда на пластинах конденсатора в момент времени t=0;  - частота затухающих колебаний;
- частота затухающих колебаний;  - собственная частота;
- собственная частота;  - коэффициент затухания.
- коэффициент затухания.
· Логарифмический декремент затухания:
 ,
,
где R – активное сопротивление контура; L – индуктивность контура; ω – частота затухания контура.
· Добротность Q контура:
 ,
,
где  - энергия, запасенная в контуре к моменту времени t;
- энергия, запасенная в контуре к моменту времени t;  - уменьшение энергии за период колебаний Т.
- уменьшение энергии за период колебаний Т.
В случае слабого затухания добротность:
 .
.
1.8 Вынужденные электрические колебания.
· Уравнение, описывающее изменения заряда на конденсаторе и установившиеся вынужденные колебания при последовательном включении в контур напряжения  :
:
 ,
,  ,
,
где  ;
; 
( 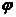 – сдвиг по фазе между зарядом и приложенным напряжением).
– сдвиг по фазе между зарядом и приложенным напряжением).
· Сила тока при установившихся колебаниях:
 ,
,
где амплитуда тока:
 .
.
Силу тока можно записать в виде:
 ,
,
где 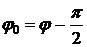 - сдвиг по фазе между током и приложенным напряжением.
- сдвиг по фазе между током и приложенным напряжением.
Этот сдвиг по фазе  находят по формуле:
находят по формуле:
 .
.
1.9 Упругие (механические) волны – механические возмущения, распространяющиеся в упругой среде.
· Уравнение плоской волны, распространяющейся вдоль положительного направления оси х в однородной непоглощающей среде:
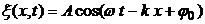
или
 ,
,
где  - смещение точек среды с координатой х в момент времени t; А - амплитуда волны; ω – циклическая частота волны;
- смещение точек среды с координатой х в момент времени t; А - амплитуда волны; ω – циклическая частота волны;  – начальная фаза волны (определяется выбором начала отсчета x и t); υ – фазовая скорость; k – волновое число.
– начальная фаза волны (определяется выбором начала отсчета x и t); υ – фазовая скорость; k – волновое число.
· Фаза волны:
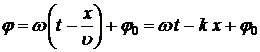 .
.
· Длина волны:
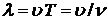 .
.
· Волновое число:
 .
.
· Волновой вектор – вектор 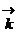 , направленный по нормали к волновой поверхности, а модуль, которого равен волновому числу k.
, направленный по нормали к волновой поверхности, а модуль, которого равен волновому числу k.
· Уравнение плоской волны, распространяющейся в направлении, определяемом волновым вектором  :
:
 .
.
· Уравнение сферической волны:
 ,
,
где r – расстояние от центра волны до рассматриваемой точки среды. Это уравнение справедливо лишь для r, превышающих размеры источника.
· Фазовая υ и групповая U скорости, а также связь между ними:
 ;
;  ;
;  .
.
· Скорость распространения звуковых волн в газах:
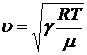 ,
,
где R – универсальная газовая постоянная; µ - молярная масса газа;  - отношение молярных теплоемкостей газа при постоянном давлении и объеме; T – термодинамическая температура.
- отношение молярных теплоемкостей газа при постоянном давлении и объеме; T – термодинамическая температура.
2.0 Электромагнитные волны.
· Уравнения плоской электромагнитной волны:
 ;
;
 ,
,
где 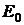 и
и  - соответственно амплитуды напряженностей электрического и магнитного полей волны; ω – циклическая частота;
- соответственно амплитуды напряженностей электрического и магнитного полей волны; ω – циклическая частота;  - волновое число;
- волновое число;  – начальная фаза колебаний в точках с координатой х=0.
– начальная фаза колебаний в точках с координатой х=0.
· Фазовая скорость электромагнитной волны:
 ,
,
где  - скорость распространения света в вакууме;
- скорость распространения света в вакууме;  и
и  - соответственно электрическая и магнитная постоянные;
- соответственно электрическая и магнитная постоянные;  и
и 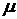 - соответственно электрическая и магнитная проницаемости среды.
- соответственно электрическая и магнитная проницаемости среды.
· Связь между мгновенными значениями напряженностей электрического Е и магнитного Н полей электромагнитной волны:
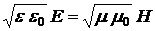 .
.
· Объемная плотность энергии электромагнитного поля:
 .
.
· Плотность потока электромагнитной волны – вектор Умова-Пойнтинга:
 ;
;  ,
,
где w – объемная плотность энергии волны,  - фазовая скорость волны.
- фазовая скорость волны.
· Интенсивность электромагнитной волны I – величина, численно равная энергии, которую переносит волна за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны:
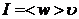 ;
;  ,
,
где <w> – среднее значение объемной плотности энергии электромагнитного поля волны;  - среднее значение модуля вектора Умова-Пойнтинга.
- среднее значение модуля вектора Умова-Пойнтинга.
Пример 1. Материальная точка участвует одновременно в двух колебательных процессах, происходящих в одном направлении по гармоническому закону с одинаковой частотой, амплитудами А1=5 см и А2=10 см и сдвигом по фазе  . Определить амплитуду и начальную фазу результирующего процесса.
. Определить амплитуду и начальную фазу результирующего процесса.
Дано: А1=5 см; А2=10 см;  .
.
Найти: А;  .
.
Решение. Законы движения для каждого из процессов могут быть записаны в виде:
 ,
,  ,
,
где  ,
,  - смещения от общего для обоих процессов положения равновесия; ω – циклическая частота. (Поскольку начальная фаза
- смещения от общего для обоих процессов положения равновесия; ω – циклическая частота. (Поскольку начальная фаза  определяется выбором начала отсчета времени, можно положить
определяется выбором начала отсчета времени, можно положить  =0,
=0,  =
= 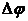 ).
).
Закон движения точки, участвующей в двух колебательных процессах:
 , (1)
, (1)
где x – результирующее смещение точки от положения равновесия.
Поскольку оба колебания гармонические с одинаковой частотой и одного направления, результирующее колебание точки гармоническое с той же частотой и закон движения может быть записан также в виде:
 , (2)
, (2)
где А – амплитуда результирующего колебания;  – его начальная фаза, равная сдвигу по фазе относительно первого колебания.
– его начальная фаза, равная сдвигу по фазе относительно первого колебания.
Неизвестные А и  могут быть найдены либо аналитическим методом, либо методом векторного сложения колебаний.
могут быть найдены либо аналитическим методом, либо методом векторного сложения колебаний.
Ø Аналитический метод. Согласно уравнений (1) и (2) получим:
 . (3)
. (3)
Используя формулы косинуса суммы двух углов, перепишем уравнение (3):
 .
.
Это уравнение будет тождеством относительно переменной t, если коэффициенты при (  ) и (
) и (  ) в левой части тождества равны соответствующим коэффициентам в правой части:
) в левой части тождества равны соответствующим коэффициентам в правой части:
 ;
; 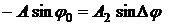 .
.
Решая эту систему уравнений относительно неизвестных А и  , получаем:
, получаем:
 ;
;
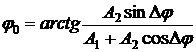 .
.
Ø Векторный метод. Любой гармонический процесс можно привести в однозначное соответствие с вращением вектора  с угловой скоростью ω , равной циклической частоте колебаний. Модуль вектора
с угловой скоростью ω , равной циклической частоте колебаний. Модуль вектора  равен амплитуде колебаний, угол
равен амплитуде колебаний, угол  , образованный этим вектором с осью ох, равен начальной фазе колебаний. Проекция вектора
, образованный этим вектором с осью ох, равен начальной фазе колебаний. Проекция вектора  на ось ох в любой момент времени будет меняться по гармоническому закону:
на ось ох в любой момент времени будет меняться по гармоническому закону:
 .
.
 При сложении колебаний, происходящих с одинаковой частотой, угол между векторами
При сложении колебаний, происходящих с одинаковой частотой, угол между векторами 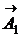 и
и  не изменяется с течением времени и равен Δφ – разности начальных фаз. Поэтому при сложении таких колебаний все векторы можно показать для момента t=0. Векторы
не изменяется с течением времени и равен Δφ – разности начальных фаз. Поэтому при сложении таких колебаний все векторы можно показать для момента t=0. Векторы 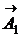 и
и  показаны на рис.3 (
показаны на рис.3 (  ), (
), (  ).
).
Рис.3
Вектор 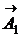 направлен вдоль оси ох, поскольку начало отсчета времени выбрано так, что
направлен вдоль оси ох, поскольку начало отсчета времени выбрано так, что  . Угол наклона вектора
. Угол наклона вектора  к оси ох равен
к оси ох равен  .
.
Согласно теореме косинусов амплитуда результирующего колебания:
 .
.
Угол наклона вектора  к оси ох и будет начальной фазой результирующего колебания:
к оси ох и будет начальной фазой результирующего колебания:
 ,
,
причем  ,
,  , откуда
, откуда 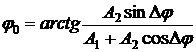 .
.
Таким образом, оба метода дают достаточно простые решения задачи.
Выполним вычисления:
 =13 см.
=13 см.
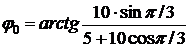 =410=0,23 π.
=410=0,23 π.
Ответ: А=13 см,  =0,23 π.
=0,23 π.
Пример 2. Математический маятник длины l=50 см совершает небольшие колебания в среде, в которой коэффициент затухания δ=09 с-1. Определить время τ и число полных колебаний N, по истечении которых амплитуда маятника уменьшится в пять раз. Во сколько раз должен возрасти коэффициент трения, чтобы колебания оказались невозможными?
Дано: l=50 см=0,50 м; δ=09 с-1.
Найти: τ, N,  .
.
Решение: При отсутствии трения колебания маятника в вертикальной плоскости происходят по гармоническому закону с собственной циклической частотой:
 . (1)
. (1)
Вследствие трения колебания маятника будут затухающими:
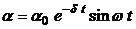 ,
,
где α – угол отклонения нити маятника от вертикали в момент t. (Записанный закон движения соответствует такому началу отсчета времени, что при t=0 маятник проходит через положение равновесия, т.е. α=0).
Период затухающих колебаний:
 , (2)
, (2)
а амплитуда A затухающих колебаний изменяется со временем по экспоненциальному закону:
 . (3)
. (3)
Запишем выражение (3) для моментов времени t и t+τ:
 ,
,  .
.
Отношение амплитуд  . Логарифмируя это выражение, находим
. Логарифмируя это выражение, находим
 .
.
Число полных колебаний, прошедших за время τ, равно отношению:
 .
.
Определим из выражения (1) собственную циклическую частоту математического маятника и, подставив её в выражение (2), получим:
 .
.
Из сравнения T и τ видно, что 1<N<2 (  ), т.е. по прошествии двух полных колебаний амплитуда уменьшится уже больше, чем в 5 раз, что соответствует уменьшению энергии маятника больше, чем в 25 раз (полная энергия колебательного движения маятника пропорциональна квадрату амплитуды,
), т.е. по прошествии двух полных колебаний амплитуда уменьшится уже больше, чем в 5 раз, что соответствует уменьшению энергии маятника больше, чем в 25 раз (полная энергия колебательного движения маятника пропорциональна квадрату амплитуды,  ).
).
Затухающие колебания по записанному выше закону возникают только при условии δ < ω0 (это очевидно из выражения периода (2): при δ > ω0 период и циклическая частота оказываются мнимыми величинами). При  происходит апериодический процесс.
происходит апериодический процесс.
Предельное значение коэффициента затухания δ , при котором возможны колебания, δmax = ω0, причем  , где m – масса маятника, постоянная по условию задачи; r – коэффициент трения. Следовательно, искомое значение отношения коэффициентов трения:
, где m – масса маятника, постоянная по условию задачи; r – коэффициент трения. Следовательно, искомое значение отношения коэффициентов трения:
 .
.
Ответ: τ=1,79 с; N=1;  =4,9.
=4,9.
Пример 3. В вакууме вдоль оси х распространяется плоская электромагнитная волна. Интенсивность волны, т.е. средняя энергия, проходящая через единицу поверхности за единицу времени, составляет 21,2 мкВт/м2. Определить амплитуду напряженности электрического поля волны.
Дано:  =1; μ=1; I=21,2 мкВт/м2=2,12×10-5 Вт/м2.
=1; μ=1; I=21,2 мкВт/м2=2,12×10-5 Вт/м2.
Найти: Е0.
Решение: Так как интенсивность электромагнитной волны определяется как средняя энергия, проходящая через единицу поверхности за единицу времени, то
 , (1)
, (1)
где <S> – среднее значение модуля вектора плотности потока электромагнитной энергии – вектора Умова-Пойнтинга. Согласно определению,
 ,
,
где E и H – соответственно мгновенные значения напряженностей электрического и магнитного полей волны, описываемые уравнениями:
 ;
;
 ,
,
где E0 и H0 – соответственно амплитуды напряженностей электрического и магнитного полей волны; ω – циклическая частота; k=ω/υ – волновое число (  - начальная фаза колебаний принята равной нулю).
- начальная фаза колебаний принята равной нулю).
Мгновенное значение модуля вектора Умова-Пойнтинга:
 ,
,
а его среднее значение, учтя, что  :
:
 . (2)
. (2)
В бегущей электромагнитной волне мгновенные значения E и H в любой точке связаны соотношением:
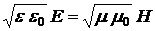 ,
,
откуда (учтя, эта электромагнитная волна распространяется в вакууме):
 . (3)
. (3)
Подставим (3) в (2) и учитывая (1), получим искомую амплитуду напряженности электрического поля волны:
 .
.
Выполним вычисления:
 .
.
Ответ: 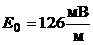 .
.
Интерференция света
2.1 Скорость света в среде:
 ,
,
где c – скорость света в вакууме, с =  м/с;
м/с;  – абсолютный показатель преломления среды.
– абсолютный показатель преломления среды.
2.2 Оптическая длина пути световой волны:
 ,
,
где  − геометрическая длина пути световой волны в среде с показателем преломления n.
− геометрическая длина пути световой волны в среде с показателем преломления n.
2.3 Оптическая разность хода двух световых волн:
 .
.
2.4 При отражении света от оптически более плотной среды фаза колебаний светового вектора (  ) испытывает скачок фазы на
) испытывает скачок фазы на  . Изменение фазы колебаний на
. Изменение фазы колебаний на  приводит к изменению оптического пути световой волны на
приводит к изменению оптического пути световой волны на  . (
. (  - длина волны в вакууме).
- длина волны в вакууме).
 2.5 Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки, находящейся в воздухе, рис. 4:
2.5 Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки, находящейся в воздухе, рис. 4:
 ,
,
где d – толщина пластинки (пленки); i − угол падения луча на пластинку;  − длина световой волны в вакууме.
− длина световой волны в вакууме.
Слагаемое  учитывает изменение оптической длины пути световой волны при отражении ее от среды, оптически более плотной (в точке А).
учитывает изменение оптической длины пути световой волны при отражении ее от среды, оптически более плотной (в точке А).
2.6 Условие максимумов интенсивности света при интерференции:
 (
(  = 0, 1, 2, 3,…).
= 0, 1, 2, 3,…).
2.7 Условие минимумов интенсивности света при интерференции:
 (
(  = 0, 1, 2, 3,…).
= 0, 1, 2, 3,…).
2.8 Кольца Ньютона. При отражении света от поверхностей воздушной прослойки, образованной между стеклянной пластинкой и соприкасающейся к ней выпуклой поверхностью линзы с радиусом кривизны  , рис. 5, возникающая интерференционная картина носит название колец Ньютона.
, рис. 5, возникающая интерференционная картина носит название колец Ньютона.
· В отраженном свете оптическая разность хода лучей при отражении от поверхностей воздушной прослойки:
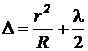 .
.
·  Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем):
Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем):
 ,
,
где k – номер кольца (k = 1, 2, 3,…);
R – радиус кривизны поверхности линзы.
· Радиусы темных колец в отраженном свете (или светлых в проходящем):
 .
.
Пример 4. Поверхности стеклянного клина (n = 1,5) образуют между собой угол  . На клин падает нормально к его поверхности пучок монохроматических лучей длинной волны
. На клин падает нормально к его поверхности пучок монохроматических лучей длинной волны  = 0,5 мкм (рис. 6). Найти расстояние между полосами.
= 0,5 мкм (рис. 6). Найти расстояние между полосами.
Дано: n = 1,5;  ;
;  = 0,5 мкм = 0,5
= 0,5 мкм = 0,5  м.
м.
Найти:  .
.
 Решение. Клин представляет собой частный случай тонкой пленки, имеющей переменную толщину d. Когерентные волны образуются при отражении света от верхней и нижней граней клина. При малых углах
Решение. Клин представляет собой частный случай тонкой пленки, имеющей переменную толщину d. Когерентные волны образуются при отражении света от верхней и нижней граней клина. При малых углах
клина  когерентные лучи 1 и 2 идут практически параллельно и
когерентные лучи 1 и 2 идут практически параллельно и
интерферируют (рис. 6а). Оптическую разность хода этих лучей находим по формуле
 .
.
В данной задаче угол падения лучей на клин i = 0 и разность хода  приблизительно равна
приблизительно равна
 .
.
Пусть точкам С1 и С2 на рис. 6 б соответствуют две соседние светлые интерференционные полосы, тогда для разностей хода  и
и  в этих точках имеем:
в этих точках имеем:
 ,
,
 ,
,
где dk, dk-1 – толщины клина в тех местах, где наблюдаются светлые полосы; k, (k-1) – номера полос (номера интерференционных максимумов).
Вычитая почленно эти два равенства друг из друга, получим:
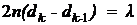 ,
,
откуда
 . (1)
. (1)
Искомое расстояние между соседними полосами  можно легко выразить из
можно легко выразить из  :
:

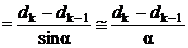 ,
,
sin  , так как по условию задачи угол
, так как по условию задачи угол  очень мал.
очень мал.
Подставляя в последнюю формулу вместо разности  ее значение из формулы (1), получим:
ее значение из формулы (1), получим:

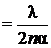 .
.
Найдем численное значение  (
(  =0,5 мкм=0,5
=0,5 мкм=0,5  , n = 1,5).
, n = 1,5).
Переведем  в радианы (
в радианы (  = 3,14):
= 3,14):
 рад;
рад;  рад;
рад;
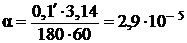 рад.
рад.
Тогда получим:

 .
.
Ответ: 
 мм.
мм.
Эта задача может быть решена и в обратном порядке, то есть по расстоянию между интерференционными полосами  можно найти угол клина
можно найти угол клина  .
.
Дифракция света
Дифракция света на одной щели при нормальном падении лучей.
· Условие минимумов интенсивности света:
 , (k = 1, 2, 3,…),
, (k = 1, 2, 3,…),
где а – ширина щели;  – угол дифракции; k – номер минимума.
– угол дифракции; k – номер минимума.
· Условие максимумов интенсивности света на щели:
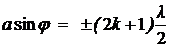 , (k = 1, 2, 3,…).
, (k = 1, 2, 3,…).
3.2 Дифракция света на дифракционной решетке при нормальном падении лучей.
· Условие главных максимумов интенсивности:
 (k = 0, 1, 2 ,…),
(k = 0, 1, 2 ,…),
где d – период (постоянная) решетки; k – номер главного максимума;
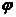 – угол между нормалью к поверхности решетки и направлением на данный максимум.
– угол между нормалью к поверхности решетки и направлением на данный максимум.
3.3 Разрешающая способность дифракционной решетки:

где k – порядок дифракционной картины, N – число штрихов решетки, 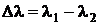 - минимальная разница двух разрешаемых световых волн с длинами волн
- минимальная разница двух разрешаемых световых волн с длинами волн  и
и  .
.
3.4 Формула Вульфа-Брегга. Условие дифракционных максимумов:
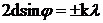 (k = 0, 1, 2 ,…),
(k = 0, 1, 2 ,…),
где d – расстояние между атомными плоскостями кристалла, 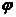 - угол скольжения (угол между направлением пучка параллельных лучей, падающих на кристалл, и гранью кристалла).
- угол скольжения (угол между направлением пучка параллельных лучей, падающих на кристалл, и гранью кристалла).
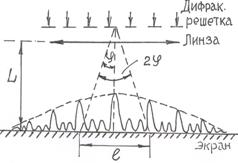
Пример 5. На дифракционную решетку Д падает монохроматический свет с длинной волны  = 0,65 мкм. На экране Э, расположенном параллельно решетке и отстоящем от нее на расстояние L = 0,6 м, наблюдается дифракционная картина (рис. 7). Расстояние между дифракционными максимумами первого порядка на экране
= 0,65 мкм. На экране Э, расположенном параллельно решетке и отстоящем от нее на расстояние L = 0,6 м, наблюдается дифракционная картина (рис. 7). Расстояние между дифракционными максимумами первого порядка на экране  =10 см. Определить постоянную дифракционной решетки d и общее число главных максимумов, получаемых с помощью этой решетки.
=10 см. Определить постоянную дифракционной решетки d и общее число главных максимумов, получаемых с помощью этой решетки.
Дано:  ; L = 0,6 м;
; L = 0,6 м;  =0,1 м; k = 1.
=0,1 м; k = 1.
Найти: d; N.
Решение. 1. Запишем условие главных максимумов для дифракционной решетки:
 . (1)
. (1)
где d – период решетки, k – порядок максимума.
Для того чтобы найти постоянную решетки d, необходимо знать угол  , под которым получается k – й максимум.
, под которым получается k – й максимум.
По условию задачи k = 1. Так как  << L (рис. 7), то можно считать, что
<< L (рис. 7), то можно считать, что
sin  1
1  tg
tg  1 =
1 =  . (2)
. (2)
Подставляя формулу (2) в формулу (1), получим :
 ;
;  .
.
Находим числовое значение:

Рис.7
2.Для определения общего числа главных максимумов N, даваемых дифракционной решеткой, исходим из условия, что максимальный угол отклонения лучей от нормального направления распространения не может превышать 900, а  .
.
Тогда, используя формулу (1), находим максимальное значение kmax:
 . (3)
. (3)
Производим вычисления:
 .
.
Общее число максимумов N = 2kmax + 1,то есть слева и справа от центрального (нулевого) максимума будут наблюдаться по одинаковому числу максимумов, равному kmax, то есть всего 2kmax. Если учесть центральный нулевой максимум, получим общее число максимумов:
N =  .
.
Ответ: d = 7,8 мкм; N = 25.
Если по формуле (3) kmax получится не целым числом, то за число максимумов нужно брать целую часть получившегося числа.
Поляризация света
4.1 Закон Брюстера:
 ,
,
где iб – угол падения, при котором отраженная световая волна полностью поляризована; n2,1 – относительный показатель преломления среды, от которой происходит отражение света.
4.2 Закон Малюса:
 ,
,
где I – интенсивность плоскополяризованного света, вышедшего из анализатора;
I0 – интенсивность плоскополяризованного света, падающего на анализатор;
 – угол между направлением колебаний светового вектора волны, падающей на анализатор, и плоскостью пропускания анализатора.
– угол между направлением колебаний светового вектора волны, падающей на анализатор, и плоскостью пропускания анализатора.
4.3 Угол поворота  плоскости поляризации оптически активными веществами определяется по следующим формулам:
плоскости поляризации оптически активными веществами определяется по следующим формулам:
· в твердых телах^
 ,
,
где  – постоянная вращения; d – длина пути, пройденного светом в оптически активном веществе;
– постоянная вращения; d – длина пути, пройденного светом в оптически активном веществе;
· в растворах:
 ,
,
где с – массовая концентрация оптически активного вещества в растворе.
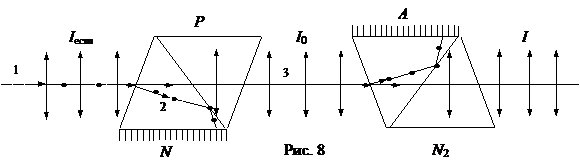
Пример 6. Какой угол образуют плоскости поляризации двух николей, если интенсивность света, вышедшего из второго николя, была ослаблена в 5 раз? Учесть, что поляризатор поглощает 10%, а анализатор – 8% падающего на них светового потока (рис.8).
Дано:  = 5; k1 = 0,1; k2 = 0,08.
= 5; k1 = 0,1; k2 = 0,08.
Найти:  .
.
Решение. Естественный луч 1 (Iecm), падая на грань призмы Николя N1, претерпевает двойное лучепреломление. В результате возникают два луча: обыкновенный 2 и необыкновенный 3 (рис. 8). Оба луча поляризованы во взаимно перпендикулярных плоскостях, интенсивность их одинакова и составляет половину интенсивности естественного света. Обыкновенный луч 2 вследствие полного отражения отбрасывается на зачерненную поверхность призмы и поглощается ею. Необыкновенный луч 3 проходит через николь. При этом и интенсивность изменяется: уменьшается еще и вследствие поглощения в веществе николя.
Таким образом, интенсивность света I0, прошедшего через первую призму (поляризатор Р), с учетом поглощения равна
 ,
,
где Iecm – интенсивность естественного света, падающего на первый николь;
k1 – относительная потеря интенсивности света в поляризаторе.
Поляризованный луч 3 интенсивности I0, попадая на второй николь (анализатор А), также расщепляется на обыкновенный, который полностью поглощается в николе 2, и необыкновенный.
Интенсивность необыкновенного пучка света I, вышедшего из анализатора, определяется законом Малюса:
I = I0cos2  ,
,
где  – угол между плоскостями пропускания поляризатора и анализатора.
– угол между плоскостями пропускания поляризатора и анализатора.
Учитывая потери интенсивности света во втором николе, получим:
I = I0(1 – k2)cos2  .
.
Искомое уменьшение интенсивности при прохождении света через оба николя будет
I =  .
.
Выразим cos2  :
:
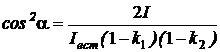 .
.
Но по условии задачи
 , то есть
, то есть  .
.
Значит,
 .
.
Искомый угол:  .
.
Ответ:  .
.
Законы теплового излучения
В данном разделе использованы новые термины, рекомендованные Международной организацией по стандартизации (ИСО).
В табл. 1 указаны наименования величин новые и соответствующие им прежние, которые вы можете встретить в литературе.
Таблица 1
| Новое наименование | Прежнее наименование |
Излучательность, Re
Спектральная плотность излучательности,  Облученность, Ее
Облученность, Ее
| Энергетическая светимость, Re
Спектральная плотность энергетической светимости,  Энергетическая освещенность, Ее
Энергетическая освещенность, Ее
|
5.1 Поток энергии (мощность излучения) – энергия электромагнитного излучения, испускаемого телом за единицу времени:
 .
.
5.2 Излучательность (энергетическая светимость) тела – поток энергии, испускаемый единицей поверхности излучающего тела по всем направлениям:
 .
.
5.3 Спектральная плотность излучательности (спектральная плотность энергетической светимости) – поток энергии с единицы площади поверхности тела, приходящийся на единичный интервал длин волн, выбранный около конкретной длины волны  :
:
 .
.
5.4 Закон Стефана-Больцмана:
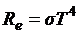 .
.
где Re – излучательность абсолютно черного тела; Т – термодинамическая температура тела;  – постоянная Стефана-Больцмана,
– постоянная Стефана-Больцмана,  Вт/(м2
Вт/(м2  ).
).
5.5 Излучательность серого тела:
 .
.
где аТ – коэффициент черноты (коэффициент излучения) серого тела.
5.6 Закон смещения Вина:
 .
.
где 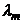 – длина волны, на которую приходится максимум энергии излучения черного тела; b – постоянная закона смещения Вина,
– длина волны, на которую приходится максимум энергии излучения черного тела; b – постоянная закона смещения Вина,  .
.
5.7 Зависимость максимальной спектральной плотности излучательности абсолютно черного тела от температуры:
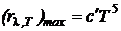 .
.
где  – постоянная величина,
– постоянная величина,  = 1,30
= 1,30  .
.
5.8 Количество лучистой энергии, излучаемой телом с поверхности площадью S за время  (при равномерном излучении):
(при равномерном излучении):
 .
.
Пример 7. Во сколько раз увеличится мощность излучения абсолютно черного тела, если максимум в спектре энергии излучения передвинется от красной границы видимого спектра (  ) к его фиолетовой границе (
) к его фиолетовой границе (  )?
)?
Дано:  ;
;  .
.
Найти: n = N2/N1.
Решение. Длина волны  , на которую приходится максимум энергии излучения абсолютно черного тела, связана с температурой тела Т законом смещения Вина:
, на которую приходится максимум энергии излучения абсолютно черного тела, связана с температурой тела Т законом смещения Вина:
 (1)
(1)
По формуле (1) определяем температуры тела Т1 и Т2:
 ;
; 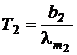 . (2)
. (2)
Мощность излучения абсолютно черного тела:
N = ReS,
где Re – излучательность; S – площадь поверхности излучающего тела.
По закону Стефана-Больцмана излучательность абсолютно черного тела:
 .
.
Отсюда выражаем мощности излучения тела при температурах Т1 и Т2:
 ,
,  .
.
Находим их отношение:
 .
.
Из формул (2) следует, что  .
.
Тогда
 .
.
Ответ:  .
.
Дата добавления: 2018-06-27; просмотров: 344; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
