Геометричне розв’язання задач лінійного програмування у випадку, коли число змінних більше двох.
Геометричний метод розв’язування задач лінійного програмування іноді можна застосовувати і у випадку, коли число змінних більше двох. Наприклад, якщо задача задана в канонічній формі і система обмежень дозволяє виразити всі змінні через які-небудь дві з них. Тоді підставляючи ці вирази в цільову функцію, одержимо функцію двох змінних. Виключаючи виражені змінні в обмеженнях, переходимо від обмежень-рівностей до обмежень-нерівностей виду (2).
Приклад 4. Знайти найбільше значення функції  при обмеженнях:
при обмеженнях:

Розв’язання. Виражаємо з обмежень задачі всі змінні через  і
і  . Спочатку з третього рівняння системи знаходимо
. Спочатку з третього рівняння системи знаходимо 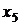 :
:  . Підставивши цей вираз в перше і друге рівняння, одержимо:
. Підставивши цей вираз в перше і друге рівняння, одержимо:

Тепер з другого рівняння можна визначити  :
:  . Підставивши вираз
. Підставивши вираз  в перше рівняння, одержимо:
в перше рівняння, одержимо:  , звідки
, звідки  . За умовою задачі змінні
. За умовою задачі змінні  ,
, 
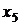 невід’ємні, тому одержимо таку систему обмежень:
невід’ємні, тому одержимо таку систему обмежень:
 або
або 
Нарешті, вирази для  ,
, 
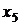 підставимо в цільову функцію і одержимо:
підставимо в цільову функцію і одержимо:
 .
.
Таким чином, ми одержали задачу для функції двох змінних: знайти найбільше значення функції  при таких обмеженнях:
при таких обмеженнях:

Побудуємо тепер многокутник  , обумовлений останньою системою обмежень, і пряму
, обумовлений останньою системою обмежень, і пряму  , задану рівнянням
, задану рівнянням 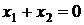 :
:
 Паралельним переносом прямої
Паралельним переносом прямої  в напрямку вектора
в напрямку вектора  , визначимо точку A многокутника
, визначимо точку A многокутника  , яка відповідає найбільшому значенню z (точку “виходу”). Координати цієї точки знаходимо з умови перетину прямих
, яка відповідає найбільшому значенню z (точку “виходу”). Координати цієї точки знаходимо з умови перетину прямих  (
(  ) і
) і  (
(  ):
):
|
|
|
 .
.
Отже, найбільше значення функції  в області, зумовленої обмеженнями задачі, досягається при
в області, зумовленої обмеженнями задачі, досягається при  ,
,  і воно дорівнює
і воно дорівнює 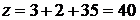 . Знайдемо тепер значення змінних
. Знайдемо тепер значення змінних  ,
, 
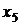 :
:
 ,
,  ,
,  .
.
Відповідь: 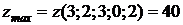 .
.
Приклад 5. Знайти мінімум цільової функції  при таких обмеженнях:
при таких обмеженнях:
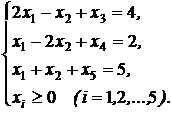
 Розв’язання. Виходячи з вигляду цільової функції, можна перейти від початкової системи обмежень-рівностей до системи обмежень-нерівностей:
Розв’язання. Виходячи з вигляду цільової функції, можна перейти від початкової системи обмежень-рівностей до системи обмежень-нерівностей:
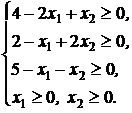
Тепер задачу можна розв’язати графічно. Побудуємо многокутник допустимих планів  .
.
Легко бачити, що цільова функція досягає мінімуму в точці  :
:
 .
.
Відповідь:  .
.
Геометричне розв’язання задач нелінійного програмування.
Загальних методів розв’язання задач нелінійного програмування не існує, тому майже завжди такі задачі вимагають творчого підходу. Іноді геометричний метод дозволяє розв’язати і задачі нелінійного програмування. Деякі випадки такого типу розглянемо на прикладах.
Приклад 6. Знайти найбільше значення функції  при обмеженнях:
при обмеженнях:

 Розв’язання. Спочатку побудуємо графічно множину допустимих планів. Це буде множина точок чверті кола радіуса 6 з центром в початку координат, яка лежить у першому квадранті:
Розв’язання. Спочатку побудуємо графічно множину допустимих планів. Це буде множина точок чверті кола радіуса 6 з центром в початку координат, яка лежить у першому квадранті:
Знайдемо опорні прямі, які визначаються лінійною формою цільової функції. Для цього із сімейства паралельних прямих  побудуємо деяку довільну пряму, наприклад, при
побудуємо деяку довільну пряму, наприклад, при  . Тепер легко бачити, що мінімальне значення цільова функція набуває при
. Тепер легко бачити, що мінімальне значення цільова функція набуває при  , а для визначення точки максимуму треба визначити координати точки
, а для визначення точки максимуму треба визначити координати точки  , тобто координати точки дотику до кола прямої, яка паралельна прямій рівня
, тобто координати точки дотику до кола прямої, яка паралельна прямій рівня  .
.
|
|
|
Пригадаємо, що дотична до кола в точці дотику перпендикулярна до радіуса. А це означає, що радіус  буде перпендикулярним і до прямої
буде перпендикулярним і до прямої  . Кутовий коефіцієнт k1 цієї прямої легко знайти:
. Кутовий коефіцієнт k1 цієї прямої легко знайти:  . Відомо, що кутові коефіцієнти двох взаємно перпендикулярних прямих задовольняють умові:
. Відомо, що кутові коефіцієнти двох взаємно перпендикулярних прямих задовольняють умові:  , звідки
, звідки  , а рівняння прямої
, а рівняння прямої  має вид:
має вид:  .
.
Тепер координати точки  знаходимо з системи двох рівнянь:
знаходимо з системи двох рівнянь:
 Þ
Þ 
Остаточно одержуємо: 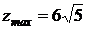 .
.
Відповідь:,  .
.
Приклад 7. Знайти найбільше і найменше значення функції 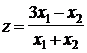 при обмеженнях:
при обмеженнях:

Розв’язання. Спочатку визначимо графічно множину допустимих планів. Це буде множина точок у першому квадранті, задана трикутником  :
:

Тепер перетворимо цільову функцію до такого виду:  .
.
Отже маємо:  . Тобто,
. Тобто,  лінійно залежить від
лінійно залежить від  . При цьому відповідна пряма проходить через початок координат, а її кутовий коефіцієнт залежить від
. При цьому відповідна пряма проходить через початок координат, а її кутовий коефіцієнт залежить від  :
:  . Проаналізуємо тепер, як саме
. Проаналізуємо тепер, як саме  залежить від
залежить від  , для цього знайдемо похідну функції
, для цього знайдемо похідну функції  :
:
|
|
|
 .
.
Оскільки ця похідна приймає тільки від’ємні значення, то це означає, що функція  спадна. Тобто, при зростанні
спадна. Тобто, при зростанні  кутовий коефіцієнт відповідної прямої
кутовий коефіцієнт відповідної прямої 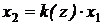 зменшується. Отже, цільова функція
зменшується. Отже, цільова функція  приймає мінімальне значення в точці
приймає мінімальне значення в точці  і досягає максимуму в точці
і досягає максимуму в точці  . Знайдемо координати цих точок і відповідні значення цільової функції.
. Знайдемо координати цих точок і відповідні значення цільової функції.
Точка  :
: 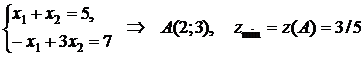 .
.
Точка  :
:  .
.
Відповідь:  ,
,  .
.
Приклад 8. Знайти найбільше і найменше значення функції  при обмеженнях:
при обмеженнях:

 Розв’язання. Визначаємо графічно множину допустимих планів. Це буде множина точок у першому квадранті, яка задана трикутником
Розв’язання. Визначаємо графічно множину допустимих планів. Це буде множина точок у першому квадранті, яка задана трикутником 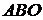 :
:
Перетворимо тепер цільову функцію до такого виду:
 .
.
Тобто, при  відповідна лінія рівня є коло. Рівняння цього кола має такий вид:
відповідна лінія рівня є коло. Рівняння цього кола має такий вид:  . Центр цього кола знаходиться в точці
. Центр цього кола знаходиться в точці 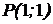 , а радіус
, а радіус  залежить від
залежить від  :
:  .
.
Тепер легко бачити, що мінімальне значення цільова функція набуває в точці 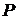 :
:  ,
,  . В точці
. В точці  :
:  ,
,  . В точці
. В точці  :
: 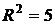 ,
,  . І нарешті в точці
. І нарешті в точці  цільова функція досягає максимуму:
цільова функція досягає максимуму:  ,
,  .
.
Відповідь:  ,
,  .
.
Приклад 9. Знайти найбільше і найменше значення функції  при обмеженнях:
при обмеженнях:

 Розв’язання. Побудуємо спочатку множину допустимих планів задачі. Це буде перетин півплощин, яки визначаються нерівностями системи обмежень задачі. Це буде многокутник
Розв’язання. Побудуємо спочатку множину допустимих планів задачі. Це буде перетин півплощин, яки визначаються нерівностями системи обмежень задачі. Це буде многокутник  .
.
|
|
|
Побудуємо лінію рівня цільової функції. Ця лінія визначається рівнянням
 .
.
Це буде коло з центром в точці  радіуса
радіуса  . На цьому колі значення функції сталі і дорівнюють
. На цьому колі значення функції сталі і дорівнюють  . При збільшенні значення
. При збільшенні значення  збільшується радіус кола і значення функції. Найменше значення функція приймає в точках кола найменшого можливого радіусу. Отже, найменше значення функція приймає в точці
збільшується радіус кола і значення функції. Найменше значення функція приймає в точках кола найменшого можливого радіусу. Отже, найменше значення функція приймає в точці  , коли радіус дорівнює нулю. Найбільше значення функція приймає в точці многокутника
, коли радіус дорівнює нулю. Найбільше значення функція приймає в точці многокутника  , найбільш віддаленої від центру кола. Це буде точка
, найбільш віддаленої від центру кола. Це буде точка  .
.
Отже,  ,
,  ,
,  ,
, 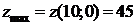 .
.
Відповідь:  ,
,  .
.
Дата добавления: 2018-05-13; просмотров: 301; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
