Активность и постоянная распада радионуклида

⇐ ПредыдущаяСтр 22 из 39Следующая ⇒

Активность A некоторого количества радиоактивного нуклида есть число спонтанных ядерных превращений dN в этом количестве радионуклида, происходящих за интервал времени dt, отнесенных к этому интервалу:

A = dN / dt (5.1)

т. е. это есть число спонтанных превращений, происходящих в радионуклиде в единицу времени.

Единицей измерения активности радионуклида является беккерель (Бк), равный 1 распаду в секунду. (Ранее использовалась единица измерения активности - кюри (Ки), равная 3,7х10¹⁰ Бк, которая с введением системы единиц СИ выведена из употребления, но до сих пор упоминается).

Число спонтанных превращений dN (t), происходящих в момент времени t за интервал времени dt, пропорционально этому интервалу и числу радиоактивных ядер вещества N (t):

dN (t) = –l N (t) dt (5.2)

Коэффициент пропорциональности l, называемый постоянной радиоактивного распада, с^–1, является характеристикой данного радионуклида; знак минус в формуле означает уменьшение числа превращений с течением времени. Решение этого уравнения определяет закон радиоактивного распада:

N (t) = N₀exp (–lt) (5.3),

в котором N₀ — число радиоактивных ядер в начальный момент времени (t = 0).

Радиоактивный распад – явление статистическое. Нельзя предсказать, когда именно распадется данное ядро, а можно лишь указать с какой вероятностью оно распадется за тот или иной промежуток времени. Распад отдельного радиоактивного ядра не зависит от присутствия других ядер и может произойти в любой интервал времени. Наблюдения за очень большим числом одинаковых радиоактивных превращений ядер позволяет установить вполне определенные количественные закономерности для характеристики процесса радиоактивного распада.

Постоянная радиоактивного распада λ определяет вероятность распада ядра в единицу времени и характеризует среднее времяжизни ядра τ:

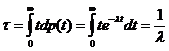(5.4)

где dp(t) – вероятность того, что ядро, прожив время t, распадется за время между t и t+dt.

Часто используемой характеристикой радиоактивного распада является период полураспада T_1/2 — это время, в течение которого распадается половина ядер радионуклида, т.е. его активность уменьшается вдвое.

Очевидна связь между T_1/2 и l, получаемая из закона радиоактивного распада:

N(T_1/2) = N₀/2 =N₀·exp(–lT_1/2 ).

Логарифмируя это выражение, получаем:

l = ln2/T_1/2 = 0,693/T_1/2 (5.5).

Следует отметить, что постоянная распада всегда приводится в с^-1_,период полураспада может выражаться в любых удобных единицах (секунды, минуты, часы, годы).

Из выражений (5.1) и (5.2) следует и связь между активностью радионуклида и числом радиоактивных ядер в нем:

A = dN/dt=lN (5.6).

Зная число радиоактивных ядер в 1см³ или в 1г радионуклидного источника, равное соответственно ρN_a/A и N_a/A, где N_a – число Авагадро, А – атомная масса, а ρ- плотность вещества источника, г/см³, можно записать связь между объемом радиоактивных ядер V, см³ или их массой m,г и их активностью:

A=lρN_a V/A=0,693ρN_a V/AT_1/2; A=lN_am/A=0,693N_a m/AT_1/2 (5.7).

Рассмотренный подход определения активности и закона радиоактивного распада относится к радионуклидам, которые в результате радиоактивных превращений переходят непосредственно в стабильный нерадиоактивный нуклид.

Однако, для радионуклидов с А > 209 часто в результате распада ядра образуется вновь радиоактивный нуклид, который в свою очередь распадается по своей схеме радиоактивных превращений и характеризуется присущим ему периодом полураспада. В итоге формируется цепочка радиоактивных нуклидов, называемая радиоактивным семейством или рядом, начинающаяся с материнского, который называется родоначальником семейства, и заканчивающаяся стабильным нуклидом. Для примера на рис.5.2 приведена такая цепочка радионуклидов радиоактивного семейства естественного ²³⁸U.

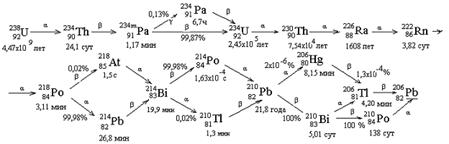
Рис.5.2. Цепочка радионуклидов семейства ²³⁸U.

В этом случае активность радионуклида в цепочке может даваться с учетом или без учета радиоактивных превращений его дочерних продуктов.

В такой ситуации временная зависимость активности к-го радионуклида в линейной цепочке радиоактивных превращений находится путем решения системы обыкновенных дифференциальных уравнений:

dN₁ (t) = –l₁ N₁ (t)dt

dN₂ (t) = –l₂ N₂ (t)dt.+l₁ N₁ (t)dt

…………………………… (5.8)

dN_к (t) = –l_к N_к (t)dt.+l_к-1 N_к-1 (t)dt

………………………………

dN_n (t) = l_n_-1 N_n_-1 (t)dt

при начальных условиях в общем случае: N₁ (t=0) =N₁₀ , N₂ (t=0) =N₂₀, … N_к (t=0)=N_к0, … N_n (t=0) =N_n₀.

В системе (5.8): N₁ (t), N₂(t),… N_к (t),… N_n (t) - число радиоактивных ядер материнского, первого и к-1-го дочерних продуктов распада и n-го стабильного нуклида, соответственно, в цепочке радиоактивных превращений; l₁,. l_{2 ,}l_{к ,} - постоянные распада соответствующих радионуклидов.

В частном случае, который широко встречается в практике, в начальный момент времени имеется только материнский радионуклид, и тогда начальные условия упрощаются: N₁ (t=0) =N₁₀ , N₂ (t=0) =0 , … N_к (t=0)=0 , … N_n (t=0) =0. Для этого случая решение системы (5.8) будет иметь вид:

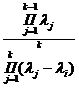= , j≠I (5.9).

Если в начальный момент времени t=0 в радиоактивном препарате присутствует помимо материнского какой–либо (i-1)-й дочерний продукт с числом ядер N_i₀ , то число ядер к-го нуклида N_k(t) при (к>i), можно представить в виде суммы ядер, образовавшихся в результате распада материнского радионуклида, и ядер, образовавшихся при распаде (i-1) дочернего продукта:

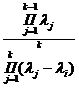= при j≠i,

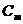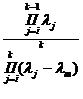= при j≠m (5.10)

По вычисленному значению N_к (t) определяется по формуле (5.6) активность к--го радионуклида A_к = l_кN_к.

Характер временного изменения активности дочерних продуктов зависит от соотношения периодов полураспада материнского и дочерних нуклидов.

На рис.5.3 демонстрируется временное изменение активности материнского и дочернего продуктов в простой линейной цепочке радиоактивных превращений при начальных условиях задачи, когда при t=0 в смеси находился только материнский радионуклид.

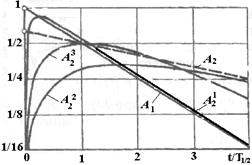
Рис.5.3. Временные кривые изменения активности материнского A₁ и дочернего продукта распада A₂ при условиях: T_1/2 дочернего< T_1/2 материнского – A₂¹ , T_1/2 дочернего> T_1/2 материнского – A₂², T_1/2 дочернего соизмерим с T_1/2 материнского – A₂³

Временной спад активности материнского радионуклида описывается простой экспонентой (в принятом масштабе – прямая линия – А₁), также, как и дочернего А₂ , если пренебречь процессом его образования при распаде материнского (показана пунктиром для условия T_1/2 дочернего > T_1/2 материнского). Активность дочернего продукта А₂¹ после достижения максимума в момент равенства скоростей его накопления и распада затем снижается, асимптотически приближаясь к прямой распада материнского нуклида, если Т_1/2 дочернего продукта меньше Т_1/2 материнского, в противном случае приближение идет к прямой распада дочернего нуклида А₂². При одинаковых периодах полураспада асимптоты не наблюдается – А₂³.

Если материнский радионуклид имеет период полураспада много больший, чем периоды полураспада его дочерних продуктов, то при больших временах t, стремящихся к бесконечности, наступает радиоактивное равновесие (вековое равновесие), при котором активности всех радионуклидов в цепочке радиоактивных превращений становятся одинаковыми. На практике это реализуется, например, для цепочек радиоактивных превращений естественных радионуклидов ²³⁸U, ²³²Th, ²²⁶Ra, и тогда указывается активность материнского радионуклида с учетом дочерних продуктов, находящихся с ним в радиоактивном равновесии.

Для протяженных источников используется понятие удельная активность – это общая активность радионуклида, приходящаяся на единицу длины, площади, объема или массы в источнике. Указанные величины носят соответственно названия линейной, поверхностной, объемной и массовой удельной активности радионуклида.

Дата добавления: 2018-05-13; просмотров: 791; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 17 18 19 20 212223 24 25 26 Следующая ⇒

Мы поможем в написании ваших работ!