Законы распределения случайной величины
Случайная величина. Числовые характеристики случайной величины. Случайные процессы.
Математическое ожидание случайной величины (с X+Y),где  ,
,  - независимые случайные величины, равно
- независимые случайные величины, равно
+ 



Дисперсия случайной величины (с X+Y),где  ,
,  - независимые случайные величины, равно
- независимые случайные величины, равно

+ 
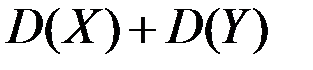

Дисперсия разности двухнезависимых случайных величин X иY равна

0
+ 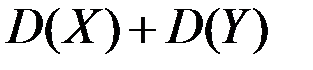

Математическое ожидание произведения двух независимых случайных величин X и Y равно



+ 
Индикатором события А называется случайная величина, которая
равна константе а>1
равна константе а<-1
всегда равна 1
+равна 1, если в результате испытания событие А происходит и равна 0, если событие А не происходит
Законом распределения дискретной случайной величины называется соответствие между
возможными значениями случайной величины и рядом натуральных чисел
+ возможными значениями случайной величины и вероятностями их появления
математическим ожиданием случайной величины и ее средним квадратическим отклонением
возможными значениями случайной величины и ее математическим ожиданием
Сумма всех вероятностей значений дискретной случайной величины равна
0

+1
-1
Математическое ожидание дискретной случайной величины вычисляется по формуле



+ 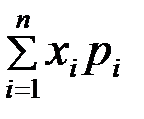
Математическое ожидание постоянной величины С равно
+С
1
0
не определено
|
|
|
Математическое ожидание случайной величины (с X-Y),где  ,
,  - независимые случайные величины, равно
- независимые случайные величины, равно
+ 



Дисперсия дискретной случайной величины определяется по формуле
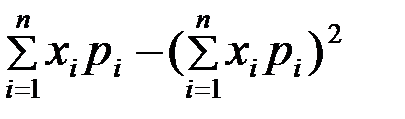
+ 


Существуют две формы задания закона распределения дискретной случайной величины:
интегральная и дифференциальная
интегральная и табличная
+табличная и графическая
графическая и интегральная
Дисперсия постоянной величины С равна
1
C
+0
не определена
Среднее квадратическое отклонение  случайной величины Х равно
случайной величины Х равно


+ 
M(X)
Дисперсия от математического ожидания  равна
равна
М(Х)
+0
Х
1
Математическое ожидание от математического ожидания 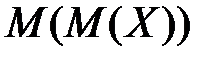 равно
равно
+M(X)
0
1
D(X)
Математическое ожидание 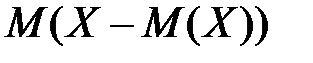 равно
равно
M(X)
D(X)
+0
1
Математическое ожидание квадрата отклонения  равно
равно
+D(X)
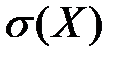
M(X)
V
Математическое ожидание M(X) случайной величины Х есть
переменная величина
+¥
-¥
+постоянная величина
Дисперсия  непрерывной случайной величины, заданной на интервале
непрерывной случайной величины, заданной на интервале  , определяется формулой
, определяется формулой
+ 



Существует две формы задания непрерывной случайной величины
+функция распределения и плотность распределения вероятностей
|
|
|
ряд распределения и полигон
функция распределения и ряд распределения
функция распределения и полигон
Выражение  является
является
дисперсией дискретной случайной величины
вариацией дискретной случайной величины
+математическим ожиданием дискретной случайной величины
средним квадратическим отклонением
Выражение  является
является
+дисперсией дискретной случайной величины
вариацией дискретной случайной величины
математическим ожиданием дискретной случайной величины
средним квадратическим отклонением
Величина, которая в зависимости от результатов испытаний принимает то или иное численное значение, называется
постоянной величиной
переменной величиной
+случайной величиной
нормальной величиной
Случайные величины делятся на
переменные и постоянные
четные и нечетные
рациональные и нерациональные
+дискретные и непрерывные
Дискретной называется такая случайная величина, которая принимает
+конечное или бесконечное счетное множество значений
бесконечное множество значений
только одно значение
только отрицательные значения
Графическая форма задания закона распределения случайной величины – это
|
|
|
парабола
прямая линия
окружность
+полигон
Табличная форма задания закона распределения случайной величины называется
суммой распределения
интегралом распределения
+рядом распределения
полем распределения
Непрерывная случайная величина имеет
конечное множество значений
бесконечное счетное множество значений
конечное или бесконечное счетное множество значений
+бесконечное несчетное множество значений
Дисперсией случайного процесса 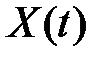 называется неслучайная функция
называется неслучайная функция  , которая при любом значении t равна
, которая при любом значении t равна
математическому ожиданию соответствующего сечения случайного процесса
+дисперсии соответствующего сечения случайного процесса
среднему квадратическому отклонению соответствующего сечения случайного процесса
вариации соответствующего сечения случайного процесса
Случайный процесс 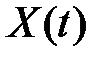 называется марковским процессом, если для любых двух моментов времени
называется марковским процессом, если для любых двух моментов времени  и
и  ,
,  , условное распределение
, условное распределение  при условии, что заданы все значения
при условии, что заданы все значения 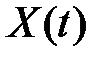 при
при 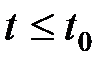 , зависит только от
, зависит только от

+ 


2Корреляционной функцией случайного процесса 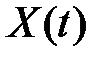 называется неслучайная функция
называется неслучайная функция  двух аргументов
двух аргументов  и
и  , которая при каждой паре значений
, которая при каждой паре значений 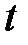 и
и  равна
равна
|
|
|
сумме математических ожиданий соответствующих сечений случайного процесса
сумме дисперсий соответствующих сечений случайного процесса
+ковариации соответствующих сечений случайного процесса
произведению дисперсий соответствующих сечений случайного процесса
Случайный процесс с дискретным временем (t принимает целочисленные значения) называется
целочисленным рядом
целочисленной последовательностью
целочисленным случайным процессом
+ временным рядом
Процесс изменения во времени состояния какой – либо системы в соответствии с вероятностными закономерностями называется
закономерным процессом
переменным процессом
+случайным процессом
составным процессом
Неслучайная функция 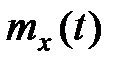 , которая при любом значении t равна математическому ожиданию соответствующего сечения случайного процесса, называется
, которая при любом значении t равна математическому ожиданию соответствующего сечения случайного процесса, называется
дисперсией случайного процесса
+математическим ожиданием случайного процесса
огибающей случайного процесса
направляющей случайного процесса
Если  , а
, а  , то дисперсия случайной величины равна
, то дисперсия случайной величины равна
+1
3
5
7
Если  , а
, а  , то
, то 
1
+5
13
16
Если  , а
, а  , то
, то 
1
3
+5
9
Если  ; а
; а  , то
, то 
1
3
+5
17
Указать неверное значение дисперсии
+-1
4
9
16
Указать верное значение дисперсии
-9
-4
+1
-1
Дискретная случайная величина принимает
только множество целых значений
только множество положительных значений
все значения из интервала 
+конечное или бесконечное счетное множество значений.
Непрерывная случайная величина принимает
множество целых значений
множество рациональных значений
конечное множество значений
+любое значение из конечного или бесконечного интервала
Для непрерывной случайной величины  и конкретного значения
и конкретного значения  вероятность
вероятность  равна
равна
+0
1/2
1

Если  -непрерывная случайная величина,
-непрерывная случайная величина,  и
и  - конкретные значения, то отсюда следует, что
- конкретные значения, то отсюда следует, что



+ 
Если  - плотность распределения, то
- плотность распределения, то  при соответствующем значении
при соответствующем значении  может принять значение
может принять значение

-2
-1
+0,5
Если  - плотность распределения, то
- плотность распределения, то  ни при каких
ни при каких  не может принять значение
не может принять значение
+-1
0,1
0,4
1
Математическое ожидание  непрерывной случайной величины
непрерывной случайной величины 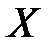 , заданной на интервале
, заданной на интервале  , определяется формулой
, определяется формулой

+ 


Если  - плотность распределения, то
- плотность распределения, то  равен
равен
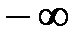
-1
0
+1
Если  - плотность распределения, то
- плотность распределения, то  определяет
определяет
+ 



Если  - плотность распределения, то
- плотность распределения, то  определяет
определяет

+ 


Если  - плотность распределения, то
- плотность распределения, то  определяет
определяет



+ 
Если  - плотность распределения, то
- плотность распределения, то  ни при каких
ни при каких  не может принять значение
не может принять значение
1
0,4
0,6
+1,2
Случайная величина, принимающая конечное или бесконечное счетное множество значений, называется
+дискретной
конечной
бесконечной
непрерывной
Случайная величина, принимающая любые значения из конечного или бесконечного интервала, называется
дискретной
конечной
бесконечной
+ непрерывной
Если  , а
, а  , то
, то 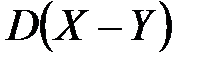 равна
равна
1
3
+5
7
Законы распределения случайной величины
График плотности нормального распределения называется
+кривой Гаусса
кривой Бернулли
кривой Пауссона
кривой Лапласа
Нормальное распределение случайной величины возникает тогда, когда варьирование случайной величины обусловлено воздействием
малого числа факторов
+большого числа факторов
редкими факторами
конечным заранее определенным числом факторов
Дискретная случайная величина, выражающая число появления события А в n независимых испытаниях, проводимых в равных условиях и с одинаковой вероятностью появления события в каждом испытании, называется распределенной по
нормальному закону
по закону Пуассона
+биномиальному закону
по показательному закону
Если случайная величина имеет биномиальное распределение, n – число независимых испытаний, а p – вероятность наступления события, то математическое ожидание вычисляется по формуле



+ 
Если случайная величина имеет биномиальное распределение, n – число независимых испытаний, а p – вероятность наступления события, то дисперсия случайной величины вычисляется по формуле
+ 



В распределении Пуассона редких событий параметр а равен
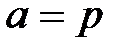
+ 


Свойство стационарности потока событий означает, что вероятность появления k событий за промежуток времени
не зависит от числа k
не зависит от величины промежутка времени
+зависит только от числа k и величины промежутка времени
не зависит ни от числа k ни от величины промежутка времени
Для расчета вероятностей ошибок при округлении показаний измерительных приборов используют
+ равномерное распределение
биномиальное распределение
распределение Пуассона
нормальное распределение
Функция надежности связана с
нормальным распределением
биномиальным распределением
равномерным распределением
+показательным распределением
Математическое ожидание равномерно распределенной случайной величины вычисляется по формуле

+ 


Дисперсия равномерно распределенной случайной величины вычисляется по формуле


+ 

Вероятность попадания равномерно распределенной случайной величины в интервал 

 вычисляется по формуле
вычисляется по формуле



+ 
Плотность распределения случайной величины с показательным распределением имеет вид
+ 



Функция распределения случайной величины с показательным распределением имеет вид

+ 
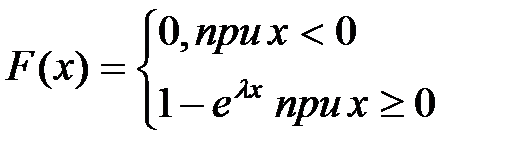

У показательного распределения математическое ожидание и среднее квадратическое отклонение
всегда различны
всегда различаются на единицу
+всегда равны
всегда равны 1
Если  - интенсивность отказов работы элемента, то 1/
- интенсивность отказов работы элемента, то 1/  - это
- это
надежность работы
скорость отказов работы
вероятность отказа
+наработка на отказ
Графиком плотности распределения равномерно распределенной случайной величины является
+ступенчатая функция
парабола
гипербола
экспонента
Для равномерно распределенной случайной величины параметр с вычисляется по формуле

+ 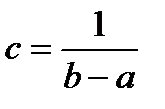
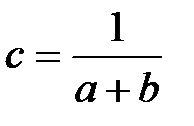

Распределение Пуассона имеет
0 параметров
два параметра
+один параметр
три параметра
Показательное распределение имеет
0 параметров
три параметра
два параметра
+один параметр
Нормальное распределение имеет
+ два параметра
0 параметров
один параметр
три параметра
Среднее квадратическое отклонение биномиально распределенной случайной величины вычисляется по формуле
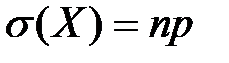
+ 


В распределении Пуассона редких событий при 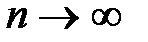


+ 

В точке  кривая Гаусса имеет
кривая Гаусса имеет
точку перегиба
точку минимума
точку разрыва
+точку максимума
Точки  и
и  являются для кривой Гаусса
являются для кривой Гаусса
+точками перегиба
точками максимума
точками минимума
точками разрыва
Функция плотности нормального распределения с математическим ожиданием  и средне – квадратическим отклонением
и средне – квадратическим отклонением  задается формулой
задается формулой
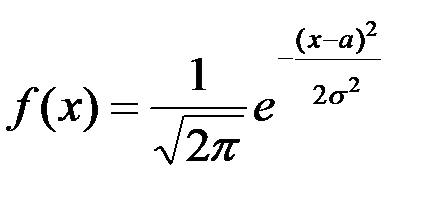
+ 


Вероятность того, что нормально распределенная случайная величина Х, имеющая математическое ожидание а и средне – квадратическое отклонение  , примет значение из интервала
, примет значение из интервала  равна
равна


+ 

Вероятность того, что отклонение нормально распределенной случайной величины Х от ее математического ожидания не превзойдет по абсолютной величине  , равна
, равна



+ 
Распределение Пуассона характеризуется тем, что его математическое ожидание и дисперсия
+ равны между собой
обратно пропорциональны друг другу
оба равны 0
отличаются друг от друга на 1
Поток событий называется простейшим, если он обладает следующими свойствами
стационарностью, отсутствием последействия, независимостью
+ стационарностью, отсутствием последействия, ординарностью
отсутствием последействия, периодичностью, непрерывностью
стационарностью, периодичностью, непрерывностью
Интенсивностью потока называется
общее число появления событий в наблюдаемый отрезок времени
среднее время между появлением событий
+среднее число появлений событий за единицу времени
общее время между появлением событий
Случайная величина, являющаяся числом появлений событий в простейшем потоке за фиксированный промежуток времени, имеет распределение
нормальное
биномиальное
показательное
+Пуассона
Непрерывная случайная величина, являющаяся промежутком времени между появлением двух событий в простейшем потоке, имеет
равномерное распределение
нормальное распределение
биномиальное распределение
+показательное распределение
Параметрами нормального распределения являются
+математическое ожидание и средне – квадратическое отклонение
функция распределения и функция плотности распределения
функция  и
и 
дисперсия и средне – квадратическое отклонение
Если плотность распределения  непрерывной случайной величины имеет вид
непрерывной случайной величины имеет вид  , где с= const, то эта случайная величина имеет
, где с= const, то эта случайная величина имеет
нормальное распределение
+ равномерное распределение
показательное распределение
биномиальное распределение
Плотность нормального распределения определяется формулой

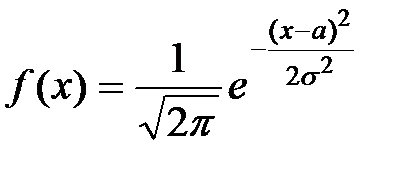

+ 
Случайная величина равномерно распределена на отрезке [2,6]. Ее дисперсия равна

3
+ 
2
Случайная величина равномерно распределена на отрезке [2,8]. Ее математическое ожидание равно
2
3
8
+5
Случайная величина имеет биномиальное распределение с параметрами n=40 и p=0,3. Ее математическое ожидание равно
3
18
+12
10
Случайная величина имеет биномиальное распределение с параметрами n=20 и p=0,4. Ее дисперсия равна
9
+4,8
13
2,1
Соответствие между возможными значениями дискретной случайной величины и вероятностями их появления называется
+законом распределения дискретной случайной величины
законом больших чисел
вероятностным соотношением
пределом дискретной случайной величины
Непрерывную случайную величину можно задать с помощью
ряда распределения
+функции распределения
полигона распределения
вероятностной таблицы
Функция распределения случайной величины  задается формулой
задается формулой


+ 

График функции распределения дискретной случайной величины представляет собой
непрерывную линию
кривую Гаусса
изображение отдельных точек на плоскости
+ступенчатую разрывную линию
Сумма величин всех скачков на графике функции распределения дискретной случайной величины равна
+1
0

произвольному числу
Графическое изображение функции плотности распределения называется
графиком распределения
+кривой распределения
графиком случайной величины
вероятностной кривой
Дисперсия непрерывной случайной величины, заданной на интервале  , вычисляется по формуле
, вычисляется по формуле


+ 

Интеграл Пуассона  равен
равен

2 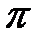

+ 
Графиком распределения равномерно распределенной случайной величины является
+непрерывная ломаная линия
непрерывная кривая
разрывная ступенчатая линия
кривая Гаусса
Функция плотности распределения случайной величины с показательным распределением имеет вид


+ 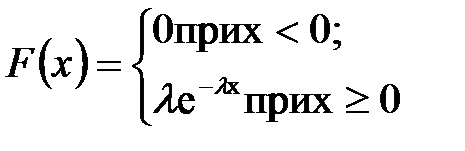

Дата добавления: 2018-05-13; просмотров: 909; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
