Неперервні випадкові величини - НВВ. Означення інтегральної функції розподілу та доведення її властивостей

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

Випадковою називається величина, яка може набувати різних числових значень. Неперервному простору елементарних подій відповідає неперервна випадкова величина. Інтегральною функцією розподілу F(x) називається функція, яка для кожного значення Х визначає ймовірність того, що випадква величина прийме значення, менше від числа х: F(x)=P(X‹x)=P(-∞‹X‹x). Свойства: ;F(-∞)=0$ F(+∞)=1; ймовірність того, шо НВВ Х прийме визначену величину =0.

Означення диференціальної функції розподілу (щільності розподілу ймовірностей) та доведення її властивостей

Якщо Х — неперервна випадкова величина, то — неперервна і диференційована; її похідна називається щільністю розподілу ймовірностей. При цьому 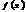— невід’ємна функція, для якої

Властивості:

1.0£F(x)£1

2.F(x) є неспадною функцією,а саме F(x₂)³F(x₁), якщо х₂>х₁

12.Означення нормального закону розподілу. Вивести формулу для імовірності попадання значень нормально розподіленої величини до заданого проміжку, наслідок. Правило "3х сигм".

. Нормальний закон розподілу задається щільністю Параметри , які входять до виразу щільності розподілу, є відповідно математичним сподіванням та середнім квадратичним відхиленням випадкової величини. Нормальний закон розподілу широко застосовується в математичній статистиці. Для обчислення ймовірності потрапляння випадкової величини, розподіленої нормально, на проміжок використовується функція Лапласа: Часто застосовується також формула: Правило трьох сигм: З практичною достовірністю (0,9973) можливо стверджувати, що значення нормально розпод. СВ Х випадають у [а-3σ;а+3σ]

Рівномірний закон розподілу

Якщо ймовірність потрапляння випадкової величини на інтервал пропорційна до довжини інтервалу і не залежить від розташування інтервалу на осі, то вона має рівномірний закон розподілу. Щільність такого розподілу:

Рівномірний закон розподілу легко моделювати. За допомогою функціональних перетворень із величин, розподілених рівномірно, можна діставати величини з довільним законом розподілу. Числові характеристики розподілу:

14. . Показниковий закон розподілу

. .

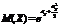Щільність розподілу випадкової величини, розподіленої за показниковим законом, задається формулою:

Випадкові величини з таким законом розподілу широко застосовуються в задачах з теорії надійності та теорії масового обслуговування. Числові характеристики:

Ме=ln2/a.

Серед усіх законів неперервних випадкових величин лише експоненціальному притаманна властивість – відсутність післядії, а саме: якщо пов”язати випадкову величину із часом, то для цього закону минуле не впливає на передбачення подій у майбутньому. Цю властивість закону використовують у харківських випадкових процесах, теорії масового обслуговування, теорії надійності.

15. Закон великих чисел, центральна гранична теорема.

Центральна гранична теорема.

Для послідовності випадкових величин 1) розглянемо:

Теорема 1. Якщо випадкові величини в послідовності (1) незалежні, однаково розподілені і для них існують моменти другого порядку, то

(2)

тобто граничним розподілом для є нормальний закон розподілу з нульовим математичним сподіванням і одиничною дисперсією.

інтегральна теорема Лапласа.

У схемі незалежних повторних випробувань

де Це випливає з того, що частоту події можна подати як суму n випадкових величин — частот настання події в окремих випробуваннях. При достатньо великих значеннях n закон розподілу цієї суми близький до нормального.

Аналогічними міркуваннями для цієї схеми легко дістати формулу:

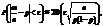де m — частота події А у n випробуваннях.

Нерівності Чебишова.

Перша форма: якщо випадкова величина Х невід’ємна і , то

Друга форма: якщо для випадкової величини існують моменти першого та другого порядку, то

Нехай задано послідовність випадкових величин:

Послідовність (1) задовольняє закон великих чисел, якщо

Окремі форми закону великих чисел різняться обмеженнями, які накладаються на випадкові величини, що входять у послідовність (1).

Теорема Бернуллі. Нехай проводиться n незалежних повторних випробувань, у кожному з яких імовірність настання події А дорівнює р. Тоді

де — частота події А у даних випробуваннях.

Теорема Чебишова

Нехай послідовність незалежних випадкових величин ,які задовольняють умовам:

1.M(X_і)>= a_і

2.D(X_і)<= с Для всіх і=1,2,3…..n

Якщо випадкові величини у послідовності незалежні, мають скінченні математичні сподівання і рівномірно обмежені дисперсії , то до послідовності (1) можна застосувати закон великих чисел. Це означає що середне арифметичне достатньо великої кількості незалежних випадкових величин дуже мало відрізняється від середнього арифметичного їхніх математичних сподівань ,взятого за абсолютним значенням .

Ця теорема є законом великих чисел ,так само як і центральна гранична теорема

Теорема Ляпунова. Якщо для незалежних випадкових величин, які утворюють послідовність , існують моменти третього порядку і виконується умова

то для виконується співвідношен-
ня (2).

16. Центральна гранична теорема. Для послідовності випадкових величин 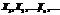розглянемо:

Теорема. Якщо випадкові величини в послідовності незалежні, однаково розподілені і для них існують моменти другого порядку, то

Інтегральна теорема Лапласа.

У схемі незалежних повторних випробувань

Аналогічними міркуваннями для цієї схеми легко дістати формулу:

де m — частота події А у n випробуваннях.

18.Вибірковий метод. Генеральна сукупність елементів. Вибірки та їх види в залежності від методів вибирання елементів. Вибірка властиво випадкова повторна і схема "неповернених куль". Незсуненість, ефективність та обгрунтованість як головні вимоги довибіркованих оцінок обраного параметра ознаки. Точкові вибіркові оцінки параметра. Довірчий інтервал вибіркової оцінки параметра. Оцінки якісних вибіркових ознак. Три типа задач вибіркового методу. Генеральною сукупністю в математичній статистиці називається множина однотипних об’єктів, кількісна чи якісна ознака яких підлягає вивченню. Підмножина об’єктів, дібраних у відповідний спосіб із генеральної сукупності, називається вибірковою сукупністю. Вважаємо, що ознака, яка вивчається, є випадковою величиною Х із функцією розподілу Результати вибірки розглядатимемо як послідовність незалежних однаково розподілених випадкових величин 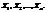Закон розподілу для всіх визначається функцією Результати вибірки — реалізації випадкових величин — позначатимемо відповідно через Розмістивши ці числа в порядку зростання і записавши частоти з якими зустрічаються ці значення, дістанемо варіаційний, або статистичний, ряд:

На підставі такого ряду можна побудувати статистичну функцію розподілу Якщо , то статистична функція розподілу збігається д теоретичної функції розподілу.

Точкові та інтервальні статистичні оцінки Статистична оцінка яка визначається одним числом, точкою, називається точковою. Беручи до уваги, що є випадковою величиною, точкова статистична оцінка може бути зміщеною і незміщеною: коли математичне сподівання цієї оцінки точно дорівнює оцінювальному параметру θ, а саме: (1) то називається незміщеною; в противному разі, тобто коли точкова статистична оцінка називається зміщеною відносно параметра генеральної сукупності θ. Різниця 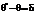(3) називається зміщенням статистичної оцінки Оцінювальний параметр може мати кілька точкових незміщених статистичних оцінок Точкова статистична оцінка називається ефективною, коли при заданому обсязі вибірки вона має мінімальну дисперсію. Отже, оцінка буде незміщеною й ефективною.

Точкова статистична оцінка називається ґрунтовною, якщо у разі необмеженого збільшення обсягу вибірки наближається до оцінювального параметра θ, а саме: Точкові статистичні оцінки є випадковими величинами, а тому наближена заміна θ на часто призводить до істотних похибок, особливо коли обсяг вибірки малий. У цьому разі застосовують інтервальні статистичні оцінки. Статистична оцінка, що визначається двома числами, кінцями інтервалів, називається інтервальною. Різниця між статистичною оцінкою та її оцінювальним параметром θ, взята за абсолютним значенням, називається точністю оцінки, а саме: (04) де δ є точністю оцінки. Оскільки є випадковою величиною, то і δ буде випадковою, тому нерівність (04) справджуватиметься з певною ймовірністю.

Дата добавления: 2018-05-13; просмотров: 624; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 Следующая ⇒

Мы поможем в написании ваших работ!