Какая функция наз. Дифференциальной функцией распред-я случ. Величины. Сформул-те свойства этой функии.
Плотностью вероятности (плотностью распределения или просто плотностью)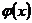 
непрерывной случайной величины Х называется производная ее функции распределения
Про случайную величину Х говорят, что она имеет распределение (распределена) с плотностью 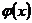на определенном участке оси абсцисс. Плотность вероятности 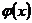, как и функция распределения F(x), является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывныхслучайных величин. Плотность вероятности иногда называют дифференциальной функцией или дифференциальным законом распределения. График плотности вероятности 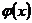называется кривой распределения.
Свойства плотности вероятности непрерывной случайной величины.
- Плотность вероятности-неотрицательная функция, т.е. 
.(как производная монотонно неубывающей функции F(х).)
- Вероятность попадания непрерывной случайной величины в интервал [а,b] равна определенному интегралу от ее плотности вероятности в пределах от а до b, т.е. 
.
☺ Согласно свойству 4 функции распределения 
. Так как F(x) - первообразная для плотности вероятности 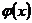(т.к. 
, то по формуле Ньютона-Лейбница приращение первообразной на отрезке [а,b] – определенный интеграл 
. ☻
Геометрически полученная вероятность равна площади фигуры, ограниченной сверху кривой распределения и опирающейся на отрезок [а,b] (рис. 3.8).
Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:
|
|
|
.
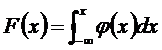Геометрически функция распределения равна площади фигуры, ограниченной сверху кривой распределения и лежащей левее точки х (рис. 3.9).
- Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице: 
.
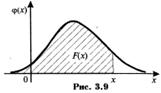Геометрически свойства 1 и 4 плотности вероятности означают, что ее график - кривая распределения - лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.
Определение матемтического ожидания дискретной и непрерывной случ величины.
Математическим ожиданием, или средним значением, М(Х) дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности:
Если дискретная случайная величина Х принимает бесконечное, но счетное множество значений x1,x2,...,xn,..., то математическим ожиданием, или средним значением, такой дискретной случайной величины называется сумма ряда (если он абсолютно сходится):
Так как данный ряд может и расходиться, то соответствующая случайная величина может и не иметь математического ожидания. Например, случайная величина Х с рядом распределения
|
|
|
не имеет математического ожидания, ибо сумма ряда 
равна ∞. На практике, как правило, множество возможных значений случайной величины распространяется лишь на ограниченный участок оси абсцисс и, значит, математическое ожидание существует.
Математическим ожиданием непрерывной случайной величиныХ, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл 
. Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле: 
. При этом предполагается, что интеграл абсолютно сходится.
Дата добавления: 2018-05-13; просмотров: 287; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!