Нормальный закон распределения.

⇐ ПредыдущаяСтр 3 из 3

В теории вероятностей и математической статистике важнейшую роль играет так называемое нормальное или гауссовское распределение. Значимость нормального распределения определяется тем, что оно служит хорошим приближением для большого числа наборов случайных величин.

НСВ Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и σ² , если ее функция плотности вероятности имеет вид:

p(x) = 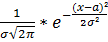, -∞<x<+∞.

Кривую нормального закона распределения называют нормальной или кривой Гаусса.

Для СВ, распределенной по нормальному закону

M(X) = a ,

D(X) = 𝜎².

Сложность нахождения функции распределения F(x) с использованием интеграла связи для нормального закона связана со сложностью нахождения интеграла вида:

F(x) =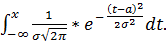

Т.к. он не берется в элементарных функциях этот интеграл можно представить через функцию Лапласа.

Ф(х) =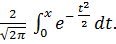

Функция распределения СВ Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле

F(x) =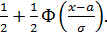

Вероятность попадания значений НСВ Х в интервал [α,β] определяется формулой

P(α ≤ x ≤ β) = F(β)-F(α) = [Ф(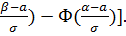

Вероятность того, что отклонение СВ Х, распределенной по нормальному закону, от математического ожидания а не превысит величину 𝜎>0 (по абсолютной величине), равна

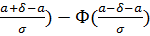p(|x-a|≤δ)=p(a-δ≤ x ≤a+δ)= [Ф( = Ф( ).

«Правило трех сигм»: Если СВ Х имеет нормальный закон распределения с параметрами a и 𝜎², т.е. N(a;𝜎²), то практически достоверно, что ее значения заключены в интервале (a-3𝜎; a+3𝜎)

P(|x-a|≤3𝜎) = Ф( 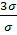) = Ф(3) = 0,9973.

Закон больших чисел.

Под этим понятием скрывается ряд теорем, которые имеют большое значение в МС.

Ая теорема: Неравенство Маркова.

Если СВ Х принимает только неотрицательные значения и имеет математическое ожидание, то для положительного числа А верны неравенства:

p(x>A) ≤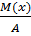

p(x≤A) ≥ 1 -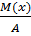

Ая теорема: Неравенство Чебышева.

Для любой СВ Х, имеющей математическое ожидание и дисперсию справедливо неравенство

P(|x-M(x)|>ɛ) ≤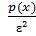

P(|x-M(x)|≤ɛ) ≥ 1 -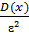

Яя теорема: Теорема Чебышева.

Если СВ х₁, х₂, …,х_n попарно независимы, дисперсии которых ограничены одной и той же постоянной величиной (D(x)≤C), то при неограниченном увеличении n(n→∞) и для сколь угодно малого числа ɛ имеет место равенство

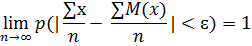
Ая теорема: Теорема Бернулли.

Частость (частота) события в n повторных независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p, при неограниченном увеличении числа n сходится по вероятности к вероятности p этого события в отдельном испытании.

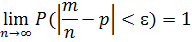
Или

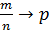Дата добавления: 2018-05-13; просмотров: 181; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 23

Мы поможем в написании ваших работ!