Угол между прямой и плоскостью
Определение: Если прямая АВ пересекает плоскость  и не перпендикулярна
и не перпендикулярна  , то угломмежду прямой АВ и плоскостью
, то угломмежду прямой АВ и плоскостью  называется угол между прямой АВ и её проекцией на плоскость
называется угол между прямой АВ и её проекцией на плоскость  .
.
| В |
АВ  =0, АВ
=0, АВ 
| А |


|

Где 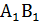 =
= 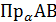

|

|
| О |

|

|
| А |

|
 =
= 
| А |
| В |
| В |

|
 =
= 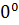
Алгоритм векторно-координатного метода:
1).Используя особенности заданной фигуры ввести в пространстве прямоугольную систему координат
2).Ввести направляющий вектор прямой  и найти его координаты
и найти его координаты
3).Ввести нормальный вектор плоскости  и найти его координаты
и найти его координаты
4).Найти 
1 случай:
| B |
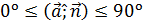

|
| A |

|
|
|

|


|

|
| B |

|
| A |
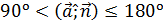

|


|
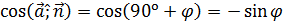

|

|
Объединив результаты и учтя, что 

|

|
Определение: Ненулевой вектор коллинеарный прямой АВ называется направляющим вектором прямой АВ.
Определение: Ненулевой вектор называется нормальным вектором плоскости, если вектор перпендикулярен к данной плоскости

|
| . |
| . |

|
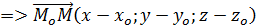
|
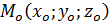

|

|

 ,
, 
 , так как , так как
|


 и
и  , то
, то
Уравнение плоскости, проходящей через точку с координатами  , с заданным нормальным вектором , с заданным нормальным вектором 
|
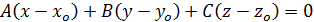
Уравнение плоскости, нормальный вектор которой 
|

Замечание: Если координаты нормального вектора  найти трудно в задаче, то можно поступить следующим образом:
найти трудно в задаче, то можно поступить следующим образом:
|
|
|
Алгоритм нахождения координат вектора  :
:
1. Предположим  , а
, а  или
или  ,
, 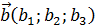
 или
или  ,
, 
 и
и  должны лежать на пересекающихся прямых.
должны лежать на пересекающихся прямых.
2. Так как  ,
,  , то есть
, то есть 
3. Найти одно из решений данной системы, то есть найти одну из троек чисел, удовлетворяющих данной системе.
Задача 2.
В прямоугольном параллелепипеде АВСD  точки Е и F середины рёбер
точки Е и F середины рёбер  и
и  соответственно. Ребра АВ и
соответственно. Ребра АВ и  равны 4. Ребро ВС равно 6. Найти тангенс угла между прямой ЕF и плоскостью основания.
равны 4. Ребро ВС равно 6. Найти тангенс угла между прямой ЕF и плоскостью основания.

|

|
| z |
| y |
| x |
| F |
| E |

|
| B |
| C |

|
| D |
| A |
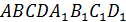 –
–
прямоугольный параллелепипед
АВ = 4,  = 4
= 4
ВС = 6
|
|
|
Е – середина 
F – середина 
Найти: 
Решение:
1) Введём прямоугольную систему координат, как показано на рисунке
2) Найдём координаты нужных точек:
B(0;0;0)
 (0;0;4)
(0;0;4)
E (4;0;2)
F(2;6;4)
3) Введём направляющий вектор прямой ЕF и найдём его координаты:
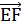 (-2;6;2)
(-2;6;2)
4) Введём нормальный вектор плоскости (ABC) и надём его координаты:
 (0;0;4)
(0;0;4)
5) Воспользуемся формулой нахождения синуса угла между прямой и плоскостью
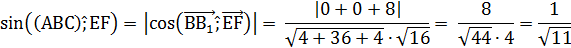
6) Так как  – острый, то
– острый, то

7) Таким образом, 
Ответ: 
Угол между плоскостями
Определение: углом между пересекающимися плоскостями называется угол, не превосходящий остальных трёх, который образуется при пересечении плоскостей.
Пусть  и и  - данные плоскости, пересекающиеся по прямой АВ. Через некоторую точку Fпрямой АВ проведём в плоскости - данные плоскости, пересекающиеся по прямой АВ. Через некоторую точку Fпрямой АВ проведём в плоскости  прямую FC⊥AB , а в плоскости прямую FC⊥AB , а в плоскости  - прямую FD⊥AB.Угол - прямую FD⊥AB.Угол  между прямыми FC и FD - угол между плоскостями между прямыми FC и FD - угол между плоскостями  и и  . .
 , , 
|

|

|

|

|

|

|

|

|
| C |
| D |
| B |
| F |
| A |

|
|
|

|

|
| (2) |
| (1) |

|

|

|

|

|

|
 , , 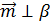
 - как углы с попарноперпендикулярными сторонами.
(1) - как углы с попарноперпендикулярными сторонами.
(1)  (2)
(2)  Объединив результаты, получаем:
Объединив результаты, получаем:
 Формула нахождения угла между плоскостями
Формула нахождения угла между плоскостями
|
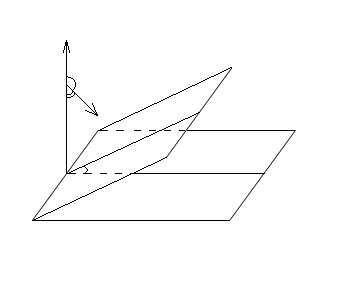
Алгоритм векторно-координатного метода:
1). Ввести прямоугольную систему координат
2.) Ввести нормальные векторы  заданных плоскостей
заданных плоскостей  и найти их координаты.
и найти их координаты.
3.) Вычислить косинус угла между векторами 
4.) Найти по формуле 
Задача 3.
В прямоугольном параллелепипеде АВСD  ребра АВ и BC равны 6. Ребро
ребра АВ и BC равны 6. Ребро  равно 4. Найти тангенс угла между плоскостями (
равно 4. Найти тангенс угла между плоскостями (  ) и
) и  .
.
| x |
| z |
| y |

|

|
| D |
| B |

|
| A |

|
| C |
Дано:  –
–
прямоугольный параллелепипед
АВ = 6
ВС = 6
 = 4
= 4
Найти: 
Решение:
1) Введём прямоугольную систему координат, как показано на рисунке
2) Найдём координаты нужных точек:
В(0;0;0)
 (0;0;4)
(0;0;4)
A(6;0;0)
 (6;6;4)
(6;6;4)
C(0;6;0)
3) Введём нормальный вектор плоскости  и надём его координаты:
и надём его координаты:
 (0;0;4)
(0;0;4)
Введём нормальный вектор плоскости  –
– 
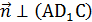



 (0;6;4)
(0;6;4)
 (-6;6;0), то
(-6;6;0), то  ,
,  , т.е.
, т.е.
 (1)
(1)
Найдём одно из решений системы (1)

Если 
4) Для нахождения косинуса угла между прямыми воспользуемся формулой:

Так как  – острый, то
– острый, то

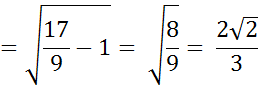
Ответ: 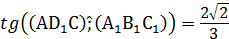
Угол между скрещивающимися прямыми
| b |
| a |

|

|

|

 AOB
AOB
Алгоритм векторно-координатного метода:
1). Введём прямоугольную систему координат и единицу измерения
2). Найдём координаты нужных точек
3).Найдём координаты направляющих векторов скрещивающихся прямых
4). Найдём угол между векторами
Задача.
В кубе АВСD  точки E и F середины рёбер соответственно
точки E и F середины рёбер соответственно  и
и  . Найдите косинус угла между прямыми АЕ и ВF
. Найдите косинус угла между прямыми АЕ и ВF
Векторно-координатный метод
|

|
| C |
| A |
| F |
| K |
 – куб
– куб

|

|
| E |
| D |
| B |
| A |

Найти: 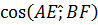
| x |
| z |
| y |
Решение:
1) Введём прямоугольную систему координат, как показано на рисунке
2) Общность задачи не нарушится, если ребро куба обозначить за 2
3) Найдём координаты нужных точек
А(2;0;0)
Е(2;1;2)
F(1;2;2)
B(2;2;0)
4) Введём направляющие векторы прямых АЕ и BF, и найдём их координаты:
 (0;1;2)
(0;1;2)
 (-1;0;2)
(-1;0;2)
5) Для нахождения косинуса угла между прямыми воспользуемся формулой:


Ответ: 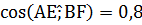
Дата добавления: 2018-05-13; просмотров: 372; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
