Нелинейные модели непрерывно-дискретных систем
Нелинейные системы автоматического регулирования
Нелинейные САР - это системы, описываемые нелинейными дифференциальными уравнениями, причем такими, которые не поддаются линеаризации методом малых отклонений. Например, дифференциальное уравнение такой системы имеет вид:
 ,
,
где F(Xвх) - нелинейная функция.
Некоторые элементы нелинейных САР имеют нелинейные статические характеристики, неподдающиеся линеаризации методом малых отклонений, или, как говорят, существенно нелинейные характеристики. Наличие в системе даже одного нелинейного элемента (все остальные линейные) делает систему в целом нелинейной.
Рассмотрим статические характеристики типичных нелинейностей, встречающихся в системах регулирования.

 Рис.1 Статические характеристики типичных нелинейных элементов
Рис.1 Статические характеристики типичных нелинейных элементов
а) – с зоной нечувствительности; б) – с насыщением; в) – с ограничением; г) – с гистерезисной петлёй люфта; д) – двухпозиционная; е) – двухпозиционная с зоной неоднозначности; ж) – трёхпозиционная.
Часто встречается нелинейные элементы со статической характеристикой, имеющей зону нечувствительности и определяемую интервалом изменения входной величины элемента: (-b < ХВХ < b), в пределах которой выходная величина не изменяется (не чувствует изменения входной величины) (Рис.1,а). Такая характеристика свойственна например электрическим исполнительным механизмам: электродвигатель при подаче на его клеммы небольшого напряжения не будет вращаться до тех пор, пока напряжение не увеличится и создаваемый им момент вращения не превысит момент трения и момент от нагрузки на валу двигателя.
|
|
|
Для большинства усилительных и исполнительных элементов характерны нелинейности с насыщением (рис.1,б) или с ограничением (рис.1,в), т.к. мощность усилителя и перемещение исполнительного механизма всегда ограничены.
В механических передачах и других устройствах встречается нелинейность называемая гистерезисной петлёй люфта (рис.1,г).
Пусть ХВХ – угол поворота ведущей шестерни редуктора;
ХВЫХ – угол поворота ведомой шестерни редуктора.
При увеличении ХВХ величина ХВЫХ остается неизменной, пока не будет выбран люфт (зазор) в зацеплении шестерен; при дальнейшем увеличении ХВХ величина ХВЫХ изменяется по прямой АВ.
После остановки в любой точке АВ и обратном движении в направлении уменьшения ХВХ величина ХВЫХ остается постоянной (горизонтальные отрезки характеристики) до тех пор, пока снова не будет выбран зазор величиной 2b, после чего ХВЫХ начнет уменьшаться по прямой DC.
Для различных электромеханических устройств типичны релейные характеристики, в которых непрерывному изменению ХВХ соответствует скачкообразное изменение ХВЫХ при определенных значениях ХВХ, а между этими значениями величина ХВЫХ остается постоянной.
|
|
|
Идеальная релейная характеристика, описывающая работу двухпозиционного реле, показана на рисунке 1,д.
Реальные двухпозиционные реле имеют статическую характеристику с зоной неоднозначности (рис.1,е), т.е. в пределах зоны неоднозначности (–b < ХВХ < +b) выходная величина может иметь значения в пределах u + C, u – C в зависимости от направления изменения ХВХ.
В случае увеличения ХВХ, переход с одного значения на другое происходит в точке +b, в случае уменьшения ХВХ переход с одного значения на другое происходит в точке –b.
Релейная характеристика с зоной нечувствительности (–b < ХВХ < +b) описывает работу трехпозиционного реле (рис.1,ж).
Кроме рассмотренных нелинейных статических характеристик, элементы автоматики могут иметь и другие нелинейные статические характеристики или даже комбинацию рассмотренных выше нелинейных статических характеристик.
Для описания проведения нелинейных систем в ТАУ существует ряд сложных методов: метод фазовой плоскости, метод гармонической линеаризации и т.д.
|
|
|
Одной из главных особенностей нелинейных систем является возникновение в них, как правило, незатухающих колебаний регулируемой величины, называемых автоколебаниями. Эти колебания не наложены извне, а являются результатом внутренних свойств нелинейной системы. Автоколебания - наиболее распространенный режим работы нелинейных систем и поэтому нелинейные системы считаются устойчивыми и тогда, когда в них возникают устойчивые автоколебания (в линейных системах автоколебания возникнуть не могут и незатухающий колебательный переходный процесс является только границей при переходе системы из устойчивой в неустойчивую).
Наиболее распространены нелинейные системы, в которых нелинейность сосредоточена в управляющем устройстве, называемом релейным регулятором. Сама система также называется релейной.
Релейные системы (регуляторы) делятся на:
1) позиционные;
2) системы (регуляторы) с постоянной скоростью исполнительного механизма.
Их статические характеристики приведены на рисунке 2.
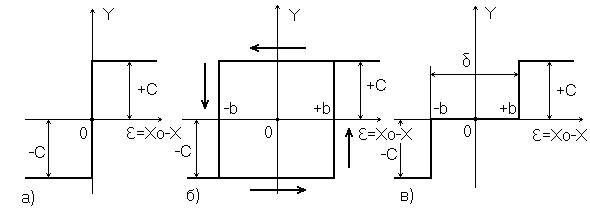
Рис.2 Статические характеристики позиционных регуляторов
А) двухпозиционный идеальный;
Б) двухпозиционный с зоной неоднозначности;
В) трехпозиционный.
|
|
|
Входной величиной служит отклонение ε регулируемой величины Х от заданного значения Х0: e=Х0-Х, а выходной - положение регулирующего органа Y. При этом за ноль принято среднее положение регулирующего органа, а +С и -С означают соответственно полное открытие (+С) и полное закрытие (-С) регулирующего органа. Регулирующим органом может быть клапан, а исполнительным механизмом – соленоид, открывающий и закрывающий его. При регулировании электрических печей регулирующий орган как таковой отсутствует, а включение и выключение нагревателей осуществляется, например, электромагнитным контактором (или может быть и бесконтактное позиционное управление мощностью). На рис.2,а – изображена статическая характеристика идеального двухпозиционного регулятора (регулирующий орган может занимать только 2 позиции - полностью открытое и полностью закрытое положение).
Реальные двухпозиционные регуляторы (рис.2,б) имеют статическую характеристику с зоной неоднозначности шириной 2b, которая вводится преднамеренно с возможностью изменения её величины.
Статическая характеристика трехпозиционного регулятора (рис.2,в) показывает, что регулирующий орган может занимать три позиции: полностью открытое (+С), полностью закрытое (-С) и среднее положение. Значение интервала –b < ε < +b называется зоной нечувствительности δ=2b.
Рассмотрим переходный процесс в релейной системе
1. график переключения регулирующего органа
Y

+C

 τ
τ
0

-C
2. переходный процесс при 2-хпозиционном регулировании








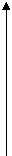 X
X
 -b
-b


 X0
X0
 +b
+b
 τ
τ
Увеличение ширины зоны неоднозначности приводит к увеличению амплитуды автоколебаний а* и периода автоколебаний Т* и уменьшению угловой частоты автоколебаний w*=2p/ Т*.
Незатухающий колебательный процесс допустим тогда, когда амплитуда автоколебаний а* укладывается в допустимые по технологическим соображениям пределы динамического отклонения регулируемой величины от заданного значения.
Рассмотрим работу трехпозиционного регулятора на примере регулирования температуры в электрической печи.
При трехпозиционном регулировании задаётся не одно значение температуры, а зона заданного значения температуры
Х0 – b < X < X0 + b, которая совпадает с зоной нечувствительности, Х0 – означает середину заданной зоны. В зависимости от величины и знака отклонения ε подается максимальная мощность Pmax, средняя мощность РСР или минимальная мощность Pmin (см. рис.3).

Рис. 3 Статическая характеристика трехпозиционного регулятора температуры

Рис. 4. а - график переключения мощности; б – переходный процесс при трехпозиционном регулировании температуры в печи
Возможны три режима:
В I режиме РСР=РН, где РН – номинальная мощность, необходимая для поддержания температуры в печи в заданных пределах. В этих условия при разогреве печи или после возмущающих воздействий температура входит в заданные пределы без возникновения автоколебаний. Температура может иметь любое значение в пределах зоны нечувствительности (в заданных пределах), т.е. точность регулирования составляет ±b.
В режиме II РСР < РН, т.е. подаваемая в средней позиции мощность недостаточна для поддержания температуры в заданных пределах. Например, уменьшилось напряжение питания, тогда температура в печи будет уменьшаться (штриховая линия) и установятся автоколебания около нижней границы заданной зоны. Система будет работать в двухпозиционном режиме при переключении мощности с РСР на Pmax и обратно.
В режиме III РСР > РН, т.е. подаваемая в средней позиции мощность больше мощности, необходимой для поддержания температуры в заданных пределах. В этом случае температура в печи будет возрастать, а затем установятся автоколебания вокруг верхней границы заданной зоны температур. Система также будет работать в двухпозиционном режиме при переключении мощности с РСР на РН и обратно.
При работе в режимах II и III средние значения температуры, вокруг которых устанавливаются автоколебания, отличаются от Х0 на величину ±b, т.е. как бы возникает статическая ошибка ХСТ=±b.
Преимущество трехпозиционного регулирования перед двухпозиционным заключается в том, что можно получить в некоторых случаях не колебательный переходный процесс, и что амплитуда и частота автоколебаний получаются меньше (при одинаковых характеристиках печи и Pmax).
Релейные системы с постоянной скоростью исполнительного механизма применяются при использовании регулируемых органов типа клапанов, заслонок и других, перемещаемых электродвигателями. Работа электрического исполнительного механизма происходит в релейном режиме, характеризуемом статической характеристикой (рис.5).

Рис.5 Статическая характеристика релейного регулятора с постоянной скоростью исполнительного механизма
Если отклонение регулируемой величины от заданного значения ε > b, то двигатель открывает регулируемый орган с постоянной скоростью dy/dτ = +υ; если ε находится в пределах зоны нечувствительности –b < ε < +b, то двигатель стоит; если ε < -b, то двигатель закрывает регулирующий орган с постоянной скоростью dy/dτ = -υ (величина скорости двигателя постоянна, а направление вращения меняется, что и характеризуется соответствующим знаком).
При использовании релейных регуляторов с постоянной скоростью ИМ в системе, как правило, также возникают автоколебания, особенно в астатических объектах.
Практика 3
Типовые динамические звенья
При анализе и синтезе САР удобно представлять их состоящими из простых элементов, называемых типовыми динамическими звеньями. Динамические звенья подразделяются только по динамическим свойствам (т.е. виду дифференциального уравнения), которые могут быть одинаковы при различной физической сущности процесса в звене, т.е. одним и тем же типом динамического звена охватываются элементы, в которых протекают разные физические процессы (электрические, тепловые, гидравлические и др.).
Типовое звено не обязательно представляет собой отдельный конструкционный элемент системы, а может быть частью такого элемента. Тогда элемент системы (объект регулирования, регулятор, чувствительный элемент и пр.) будет представляться определённым соединением типовых динамических звеньев. Типовые динамические звенья имеют общие свойства:
1. Одну входную и одну выходную величины;
2. Дифференциальные уравнения не выше 2-го порядка;
3. Пропускают сигнал только в одном направлении (детектирующие свойства) т.е. Хвх влияет на Хвых, а не наоборот
Все типовые звенья подразделяются на статические, астатические (интегрирующие), дифференцирующие и звено чистого запаздывания.
СТАТИЧЕСКИЕ ЗВЕНЬЯ
К статическим относятся такие звенья, которые при ступенчатом входном воздействии переходят из начального положения равновесия в новое равновесное состояние.
Статические звенья делятся на:
1) Пропорциональные;
2) Апериодические первого порядка;
3) Апериодические второго порядка;
4) Колебательные.
1. Пропорциональное звено
Это звено называют также усилительным и безынерционным. Звено описывается алгебраическим уравнением:
хвых = kхвх, [3.1]
где k - коэффициент передачи (усиления), имеющий размерность: единицы выходной величины, делённые на единицы входной величины (такую размерность имеют коэффициенты передачи всех статических звеньев).
Передаточная функция звена W(p) = k . [3.2]
Переходная функция h(t) = k1(t). [3.3]
Представляет собой ступенчатую функцию высотой k (рис. 3.1)

Рис. 3.1. Переходная функция пропорционального звена

Рис. 3.2. Примеры пропорциональных звеньев
Примерами пропорционального звена могут служить: рычаг (рис. 3.2,а), если входная величина перемещение (усилие) на одном конце рычага, а выходная величина – перемещение (усилие) на втором конце; зубчатая передача (редуктор), если хвх = jвх – угол поворота малой шестерни, а хвых = jвых – то же для большой шестерни (рис. 3.2,б); теплоотдача конвекцией от движущегося газа к стенке, если хвх - разность температур газа и стенки Dt = tг – tст, а хвых - количество отдаваемого тепла Q (рис. 3.2,в); потенциометрический датчик измерительного прибора, если хвх - перемещение движка реохорда L, а хвых - снимаемое о датчика напряжение Uвых (рис. 3.2,г).
Обычно пропорциональное (безынерционное) звено является некоторой идеализацией реальных звеньев, и к нему сводятся позиционные звенья, рассмотренные ниже, если можно пренебречь переходными процессами в них. В этих условиях, например, большинство датчиков самых различных физических величин относятся к пропорциональному звену.
2. Апериодическое (инерционное) звено первого порядка
Описывается дифференциальным уравнением:
 , [3.4]
, [3.4]
где k – коэффициент передачи;
Т – постоянная времени, с.
Передаточная функция звена W(p) = k/(Tp + 1); [3.5]
Переходная функция звена h(t) = k (1 – е-t/T). [3.6]
Переходная функция представляет собой экспоненту (рис. 3.3). Отрезок, отсекаемый касательной, проведенной в начальной точке, при установившемся значении выходной величины равен постоянной времени Т.

Рис. 3.3. Переходная функция апериодического звена 1-го порядка
Постоянная времени - это время, за которое выходная величина достигла бы своего установившегося значения, если бы с постоянной начальной скоростью. Чем больше Т, тем длительнее переходный процесс. Строго говоря, установившееся значение Хвых = k достигается при t ® ¥, но практически переходный процесс считается закончившимся через время t » 3Т.
Постоянная времени характеризует "инерционность" апериодического звена. Если она мала, то апериодическое звено по существу становится безынерционным.

Рис. 3.4. Примеры апериодических звеньев 1-го порядка
Примерами апериодических звеньев могут служить: электропривод постоянного токи, если входная величина - подводимое напряжение хвх = u, а выходная величина хвых = n - скорость вращения (рис. 3.4,а); промежуточный ковш МНЛЗ, если хвх = Gпр - Gcт - разность поступления и расхода жидкого металла, а хвых = Н - уровень металла в ковше (рис. 3.4,6); нагрев тела, помещённого в среду с температурой tc (теплоотдача оценивается по закону Ньютона q = a(tc – tм), где q - плотность теплового потока на нагреваемое тело; a - коэффициент теплоотдачи), если tc.- входная величина, а средняя температура тела tм - выходная величина (рис. 3.4,в); цепочка RC (рис. 3.4,г), если хвх = uвх – подводимое напряжение, хвых = uвых – снимаемое напряжение.
3. Апериодическое (инерционное) звено второго порядка
Описывается уравнением:
 . [3.7]
. [3.7]
Для этого звена корни характеристического уравнения  p2 +T1p +1 = 0 должны быть действительными, что выполняется при условии: Т1 > 2Т2.
p2 +T1p +1 = 0 должны быть действительными, что выполняется при условии: Т1 > 2Т2.
Передаточная функция звена W(p) = k/(  p2 +T1p +1). [3.8]
p2 +T1p +1). [3.8]
Знаменатель передаточной функции может быть разложен на множители. и тогда передаточная функция будет иметь вид:
W(p) = k/[(T3p+1)( T4p+1)], [3.9]
где  .
.

Рис. 3.5. Переходная функция апериодического звена 2-го порядка
Переходная функция (рис. 3.5) может быть получена по формуле Хевисайда
 . [3.10]
. [3.10]

Рис. 3.6. Примеры апериодических звеньев 2-го порядка
Примеры апериодического звена второго порядка: последовательное соединение двух пневматических ёмкостей, если входная величина хвх = Рпит, а выходная величина - давление в емкости хвых = р (рис. 3.6,а); цепочка RC (рис. 3.6,б), если хвх = uвх – подводимое напряжение, хвых = uвых – снимаемое напряжение.
4. Колебательное звено.
Дифференциальное уравнение звена обычно представляется в виде:
 , [3.11]
, [3.11]
где x - коэффициент затухания, 0 < x < 1.
Корни характеристического уравнения  равны
равны
 и у колебательного звена должны быть комплексными. Комплексные корни получаются при x < 1.
и у колебательного звена должны быть комплексными. Комплексные корни получаются при x < 1.
Передаточная функция звена:  . [3.12]
. [3.12]
Переходная функция звена:
 . [3.13]
. [3.13]
где a = x/Т , а  носит затухающий колебательный характер около значения хвых(t) » k. Ее затухание определяется действительной частью корней характеристического уравнения a, а частота - мнимой частью w. Существует характеристика переходного процесса, называемая степенью колебательности т = a/w, которая для колебательного звена находится в интервалах 0 < т < ¥. Колебательность переходного процесса может также характеризоваться степенью затухания:
носит затухающий колебательный характер около значения хвых(t) » k. Ее затухание определяется действительной частью корней характеристического уравнения a, а частота - мнимой частью w. Существует характеристика переходного процесса, называемая степенью колебательности т = a/w, которая для колебательного звена находится в интервалах 0 < т < ¥. Колебательность переходного процесса может также характеризоваться степенью затухания:
 , [3.14]
, [3.14]
где х1 и х3 - величины первой и третьей амплитуд выходных колебаний (рис. 3.7).

Рис. 3.7. Переходная функция колебательного звена
Значение степени затухания связано с действительной и мнимой частями корней характеристического уравнения колебательного звена
 , [3.15]
, [3.15]

Рис. 3.8. Примеры колебательных звеньев
Примерами колебательных звеньев могут служить колебательный LRC -контур (рис. 3.8,а), если хвх = uвх – подводимое напряжение, хвых = uвых – снимаемое напряжение и упругая механическая передача (рис. 3.8,б). В передаче имеется упругий элемент У, маховик М и демпфер Д, оказывающий сопротивление вращению вала. Входная величина хвх - угол поворота входного вала j1, выходная величина хвых - угол поворота выходного вала j2.
АСТАТИЧЕСКИЕ (ИНТЕГРИРУЩИЕ) ЗВЕНЬЯ
Это такие звенья, у которых после поступления на вход ступенчатого воздействия выходная величина не приходит к установившемуся значению (как у статических), а непрерывно изменяется. Они делятся на 2 вида:
1) Идеальное
2) Реальное
1. Идеальное интегрирующее звено.
Дифференциальное уравнение звена:
 , [3.16]
, [3.16]
где k1 – коэффициент передачи, имеющий размерность: единицы скорости изменения выходной величины, делённые на единицы входной величины.
Передаточная функция звена: W(p) = k1/p. [3.17]
Переходная функция звена: h(t) = k1t, [3.18]
(рис. 3.9,а) представляет собой прямую линию с углом наклона агсtg k1.

Рис. 3.9. Переходная функция и примеры идеального интегрирующего звена
Примеры интегрирующих звеньев: электродвигатель, если входная величина - напряжение питания, а выходная величина - угол поворота якоря j (рис. 3.9,б); кристаллизатор МНЛЗ, если входная величина - расход металла из промежуточного ковша (при постоянной скорости вытягивания слитка.), а выходная величина - уровень металла в кристаллизаторе; ванна жидкого металла в сталеплавильной печи, если входная величина - тепловой поток через поверхность ванны q, а выходная величина - изменение средней температуры металла Dtм (рис. 3.9,в)
2. Реальное интегрирующее звено (интегрирующее звено с замедлением).
Звено описывается дифференциальным уравнением:
 , [3.19]
, [3.19]
Передаточная функция звена: W(p) = k1/p(Tp+1). [3.20]
Переходная функция реального интегрирующего звена:  . [3.21]
. [3.21]
отличается от переходной функции идеального эвена в начальный момент времени, а затем переходит в прямую линию с тем же углом наклона.
Примерами реальных интегрирующих звеньев могут служить те же звенья, что показаны на рис. 3.9, если более точно, без допущений рассматривать их уравнения движения. Например, электродвигатель с постоянной скоростью будет идеальным интегрирующим звеном. Однако в момент пуска постоянная скорость установится не сразу, а с некоторым замедлением, и электродвигатель следует рассматривать как реальное интегрирующее звено.
ДИФФЕРЕНЦИРУЮЩИЕ ЗВЕНЬЯ.
Делятся на 2 вида: идеальное и реальное.
1. Идеальное дифференцирующее звено.
Дифференциальное уравнение звена
 , [3.22]
, [3.22]
где k2 – коэффициент передачи дифференцирующего звена, имеющий размерность: единицы выходной величины, делённые на единицы скорости изменения входной величины.
Передаточная функция звена W(р) = k2p. [3.23]
Переходная функция звена h(t) = k2d(t), [3.24]
где d(t) - так называемая дельта-функция, которая равна нулю всюду, кроме нулевого момента времени, где её значение стремиться к бесконечности.
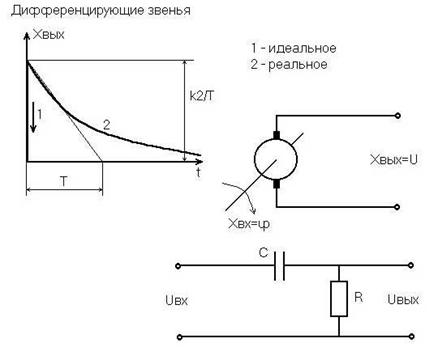
Рис. 3.10. Переходная функция и примеры дифференцирующих звеньев
Переходная функция идеального звена (рис. 3.10,а) представляет собой мгновенный бросок выходной величины в бесконечность в момент нанесения ступенчатого входного воздействия и столь же мгновенное возвращение к нулю.
Наиболее близко к идеальному звену приближается тахогенератор постоянного тока (рис. 3.10,б), если входной величиной считать угол поворота якоря, а выходной - ЭДС якоря, а также операционный усилитель в режиме дифференцирования, применяемый в аналоговых ЭВМ.
2. Реальное дифференцирующее звено (дифференцирующее звено с замедлением)
Звено описывается дифференциальным уравнением

Передаточная функция звена W(р) = k2p/(Tр + 1)
Переходная функция звена  представляет собой экспоненту, касательная к которой в точке наибольшей крутизны отсекает на нулевом значении выходной величины постоянную времени Т (рис. 3.10,а).
представляет собой экспоненту, касательная к которой в точке наибольшей крутизны отсекает на нулевом значении выходной величины постоянную времени Т (рис. 3.10,а).
Примером реального дифференцирующего звена может служить цепочка RC (рис. 3.10,в), если хвх = uвх – подводимое напряжение, хвых = uвых – снимаемое напряжение.
ЗВЕНО ЧИСТОГО ЗАПАЗДЫВАНИЯ
В отличие от других звеньев это звено описывается уравнением о запаздывающим аргументом
хвых(t) = хвх(t - t0),
где t0 - время запаздывания.
Выходная величина звена точно равна входной величине в момент времени на t0ранее.
Передаточная функция эвена (получается с использованием методов операционного исчисления)  .
.
Переходная функция звена чистого запаздывания h(t) = 1(t - t0), т.е. представляет собой единичное ступенчатое изменение выходной величины с отставанием на t0 от такого же изменения входной величины (рис. 3.11).

Рис. 3.11. Переходная функция и пример звена чистого запаздывания
Характерным примером звена чистого запаздывания служит транспортёр (например, лента агломерационной машины), на котором после изменения входной величины (толщина слоя сыпучего материала) должно пройти время t0= l/v (l - длина транспортера; v - его скорость t0 - время чистого транспортного запаздывания), после которого на ту же величину изменится выходная величина – толщина слоя сыпучего материала (рис. 3.11).
Практика 4
Типы соединения звеньев
Существуют три типа соединения звеньев между собой: последовательное, параллельное и встречно-параллельное (с обратной связью). Для математического описания систем из различно соединённых звеньев наиболее удобно пользоваться не дифференциальными уравнениями, а передаточными функциями.
1. Последовательное соединение.
Это такое соединение, при котором выходная величина предыдущего звена является входной величиной последующего звена.

Рис. 4.1. Последовательное соединение звеньев
Передаточная функция системы последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев:
W(p) = W1(p)×W2(p) ×…×Wn-1 (p) ×Wn(p). [4.1]
2. Параллельное соединение.
При параллельном соединении на вход всех звеньев поступает одна и та же входная величина хвх = хвх1 = хвх2 = ... =хвх n-1=хвх n, а выходная величина системы равна сумме выходных величин отдельных звеньев.
 .
.

Рис. 4.2. Параллельное соединение звеньев
Передаточная функция системы параллельно соединённых звеньев равна сумме передаточных функций отдельных звеньев:
W(p) = W1(p)+W2(p) +…+Wn-1 (p) +Wn(p). [4.2]
3. Соединение с обратной связью.
Таким образом может быть соединено только два звена: звено с передаточной функцией W1(р) охвачено обратной связью - звеном с передаточной функцией Wо.с.(p). При этом выходная величина всей системы равна выходной величине первого звена и входной величине звена обратной связи
хвых = хвых1 = хвх о.с.; а входная величина первого звена хвх1 = хвх ± хвых.о.с.
Знак «плюс» соответствует положительной обратной связи, знак "минус" - отрицательной обратной связи.

Рис. 4.3. Соединение с обратной связью
Передаточная функция системы при охвате звена обратной связью равна дроби, числитель которой - передаточная функция звена, а знаменатель - единица плюс (минус) произведение передаточной функции звена и передаточной функции звена обратной связи ("плюс" соответствует отрицательной обратной связи, знак "минус" - положительной обратной связи).
W(p) = W1(p)/[1 ± W1(p)×Wo.c.(p)] . [4.3]
Практика 5
Дата добавления: 2018-05-13; просмотров: 385; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
