Нормальное распределение и его свойства
Nbsp; Введение Не стоит думать, что там, где речь идет о случайных событиях бесполезно искать какие-то закономерности - случай он и есть случай. Существует несколько групп случайных явлений, в которых закономерности уже обнаружены и изучены, оценивать и сравнивать прогноз развития событий в этом случае можно и нужно. Само понятие "вероятность" нередко определяют как количественную меру возможности реализации интересующего нас случайного события. Правда, знание вероятности благоприятного исхода - это еще не выигрыш сам по себе, это лишь взвешивание возможностей. Мы ежедневно принимаем многие решения в условиях неопределенности. Принято различать неопределенность и риск. Риск - это когда можно сказать, что человек знает, на что он идет, шансы известны, вероятности оценены. Конечно, не всякую неопределенность можно превратить в риск. Но там, где это несложно сделать, это может оказать реальную помощь в принятии решения. Этот курс предназначен для руководителей (менеджеров) - практиков среднего уровня любой сферы деятельности, желающих получить базовые знания в области теории вероятностей и математической статистики в качестве основы для принятия решения в условиях неопределенности. Программа построена на основе образовательного стандарта для высшего образования в области менеджмента по дисциплине "Теория вероятностей и математическая статистика". Вместе с тем курс имеет выраженную практическую направленность, он приспособлен для решения задач, которые встречаются в курсах Школы бизнеса Открытого Университета. 2. Вероятность и риск, пространство элементарных событий В этом разделе мы введем некоторые исходные понятия теории вероятностей и начнем работать с математическим аппаратом на несложных примерах. Рассматривая интересующие нас события как элементы множеств, мы можем в дальнейшем производить над ними определенные действия, что поможет нам анализировать совокупность этих событий. Исторически первой группой случайных событий, которые были исследованы математиками, были азартные игры. Сами правила игры предполагали равноправие участников перед судьбой, при всем мастерстве игрока многое зависело от "везения". Мы также рассмотрим несколько примеров из этой области, т.к. они хорошо иллюстрируют некоторые возможности аппарата теории вероятностей, который пригодится нам в дальнейшем для других случаев. В условиях игры (в карты, в кости) математики и игроки связывают понятие вероятности выигрыша с шансом получения выигрышной комбинации по сравнению с общим числом всех возможных комбинаций. Пример 1.При падении монеты существует два возможных результата (математики называют эти результаты элементарными исходами): выпадет герб или выпадет решетка. Оба результата равновероятны, т.е. вероятность того, что монета останется лежать гербом вверх равна 50% (или 1/2), с такой же вероятностью выпадет другая сторона. Какой бы результат не загадал игрок как благоприятный для себя, его шанс выиграть и вероятность проиграть одинаковы. Пример 2.При бросании игральной кости существует уже шесть возможных элементарных исходов (количество выпавших очков может меняться от 1 до 6). Если игральная кость имеет правильную форму, все шесть результатов равновероятны. Другими словами, вероятность того, что при единственном выбрасывании кости выпадет, например, шесть очков, равна 1/6. Если только эта цифра считается выигрышем при данном броске, шансов выиграть у игрока в три раза меньше, чем в прошлый раз. Если мы хотим "уровнять" шансы при бросании игральной кости с шансом выиграть при бросании монеты, нам надо изменить правила игры, например, считать выигрышем выпадение любого четного числа. Поскольку игральная кость имеет три грани с четными числами и три грани с нечетными, шансы выиграть и проиграть при единственном броске у нас будут одинаковыми (вероятность выигрыша станет равной 1/2, т.е. такой же, как при бросании монеты). Задание При подбрасывании монеты вероятность выиграть составляет 1/2, а при бросании игральной кости выигрышем считается выпадение цифры шесть (вероятность выигрыша 1/6). Чему равна вероятность проигрыша в каждом случае? Значит ли это, что играть в кости менее выгодно? Обсуждение В каждом из двух случаев вероятность выиграть и проиграть должны составить в сумме 100% или единицу, поскольку ничейный вариант в этих ситуациях невозможен. Это означает, что при бросании монеты вероятность проиграть равна 1/2, а при бросании игральной кости - 5/6. А вот вопрос о "выгодах" предложения поиграть в кости по сравнению с предложением бросить монету не так прост, как это кажется. Оставив на минуту в стороне азартные игры, обсудим одну важную для бизнеса проблему. Решение о "выгодности" любого предпринимаемого нами действия, очевидно, зависит не только от нашей оценки риска данного предприятия, но и от величины предполагаемого выигрыша по сравнению с нашими ставками. Чем меньше шансов получить выигрыш, тем больше должна быть величина этого выигрыша по сравнению со ставкой, чтобы сделать игру привлекательной для потенциальных игроков. Забота о привлекательности условий игры, конечно, распространяется только на те случаи, когда игроки принимают решение об участии в процессе добровольно и осмысленно. Так, чем рискованнее финансовые вложения, тем большую прибыль мы ожидаем получить в результате. Когда соотношение "риск - прибыльность" кажется нам неподходящим, мы ищем возможности покинуть "игру". Поэтому при любой оценке бизнес-проекта оценка рисков не менее важна, чем оценка прибыльности, по сути, это - неотъемлемая часть финансово-экономического анализа. Возвращаясь к нашему заданию, пришло время обсудить финансовые условия игры. Какой именно выигрыш покажется нам справедливым и почему? Если при бросании монеты участвуют два игрока, сделавшие одинаковые ставки, причем выигравший забирает все, то возможный выигрыш в такой игре должен вдвое превышать исходную ставку. Менее очевидный случай - бросание кости. Должен ли выигрыш в шесть раз превышать ставку игрока, и откуда возьмется эта сумма, если игроков по-прежнему только двое? Вот если бы игроков было шестеро, и каждый поставил бы на разную цифру, то при одинаковых исходных ставках получилась бы вполне справедливая игра. Выигравший забрал бы в шесть раз больше, чем поставил, но шансы каждого игрока выиграть были бы одинаковыми. Если же играют двое, причем один выигрывает, только при выпадении цифры "шесть", значит второй выигрывает при любой другой ситуации, и его шансы на выигрыш в пять раз выше. Само по себе это не означает, что игра "нечестная", просто справедливые правила должны потребовать от второго игрока сделать исходную ставку, которая будет в пять раз выше, чем ставка первого игрока. Определение 1. Совокупность всех возможных результатов опыта в теории вероятности называется пространством элементарных исходов, мы будем обозначать это пространство греческой буквой W. Элементарные исходы обозначаются как wi, где i может принимать значения от одного до максимума по числу возможных вариантов результата опыта. Для наглядности W изображают в виде некоторой области на плоскости, а элементарные исходы wi - точками в этой области. Мы будем также пользоваться математическим обозначением W={wi, i=1, ...} для описания того факта, что пространство элементарных исходов W образуется совокупностью всех элементарных исходов wi. Определение 2.Элементарные исходы могут образовывать группы, каждая из которых называется событием. Событие A, принадлежащее пространству W, (обозначается А М W, см. рисунок), наступает тогда и только тогда, когда наступает один из элементарных исходов wi, входящих в А. Пример 3. В Примере 2 событием можно считать факт выпадения четной цифры при бросании кости. Это событие наступает, когда выпадает или цифра два, или четыре, или шесть (при трех элементарных исходах из шести возможных). Мы будем пользоваться математическим обозначением А={wi, i=1, ...} для описания того факта, что событие образуется некоторой группой элементарных исходов (напомним, что событие содержится внутри пространства элементарных исходов, как говорят математики, является его подмножеством). В данном примере пространство элементарных исходов W состоит из следующих элементарных исходов: w1={1}, w2={2}, w3={3}, w4={4}, w5={5}, w6={6}. Событие А (выпадение четной цифры) можно записать как A={w2, w4, w6}. Иногда говорят, что элементарные исходы w2, w4 и w6 благоприятны для наступления события А, в то время как w1, w3 и w5, напротив, неблагоприятны для него. Сортировка всего пространства элементарных исходов на благоприятные для интересующего нас события и неблагоприятные, как мы это увидим в следующем разделе, очень важна для нашей оценки вероятности реализации этого события. Задание Из трех цифр 1, 2, 3 наудачу берутся две цифры и составляется двузначное число. Выпишите все элементарные исходы этого опыта. Составьте из элементарных исходов события А, В и С, такие что: А={число содержит цифру 1} В={число содержит только нечетные цифры} С={число четное} Запишите эти события, используя соответствующие математические обозначения. Обсуждение Пространство элементарных исходов W состоит из следующих элементарных исходов: w1={12}, w2={21}, w3={13}, w4={31}, w5={23}, w6={32} Тогда: A={w1, w2, w3, w4} B={w3, w4} C={w1, w6} Отметим, что само пространство элементарных исходов W также представляет собой событие, происходящее всегда (при любом элементарном исходе w). События, от которых в данном эксперименте "никуда не деться", называются достоверными событиями. События называютсянезависимыми, если реализация одного из них не оказывает никакого влияния на вероятность реализации другого. К этому важному свойству мы еще вернемся в следующих разделах. События называются несовместными, если они не могут произойти одновременно. Тоже очень важное свойство, мы встретимся с ним еще не раз. Пример.Элементарные исходы являются несовместными событиями при однократном опыте. Например, если мы бросили монету один раз, выпадет или решетка или герб, но, конечно, что-нибудь одно. В простейшем случае (две стороны одной монеты, шесть граней кубика) вероятность реализации каждого элементарного исхода несложно посчитать из простого здравого смысла. Задача существенно усложняется, если этих элементарных исходов очень много и их приходится определенным образом комбинировать для составления интересующего нас события. Именно в таких более сложных ситуациях на помощь приходит математика. В следующем параграфе мы познакомимся с некоторыми правилами специального раздела математики - комбинаторики. 3. Элементы комбинаторики Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий. Основная формула комбинаторики Пусть имеется k групп элементов, причем i-я группа состоит из ni элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*...*nk. Пример 1.Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n1 элементов, а вторая - из n2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n2. Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n2. Так как в первой группе всего n1 элемент, всего возможных вариантов будет n1*n2. Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться? Решение: n1=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6). Итак, N=n1*n2*n3=6*7*4=168. В том случае, когда все группы состоят из одинакового числа элементов, т.е. n1=n2=...nk=n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно nk.Такой способ выбора носит названиевыборки с возвращением. Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8? Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=54=625. Рассмотрим множество, состоящие из n элементов. Это множество будем называть генеральной совокупностью. Определение 1. Размещением из n элементов по mназывается любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов. Пример 4.Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком. Число размещений обозначается Anm и вычисляется по формуле: Замечание: n!=1*2*3*...*n (читается: "эн факториал"), кроме того полагают, что 0!=1. Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные? Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет: Определение 2. Сочетанием из n элементов по m называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов. Пример 6. Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}. Число сочетаний обозначается Cnm и вычисляется по формуле: Пример 7.Сколькими способами читатель может выбрать две книжки из шести имеющихся? Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно: Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов. Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2). Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!. Пример 8.Сколькими способами семь книг разных авторов можно расставить на полке в один ряд? Решение: эта задача о числе перестановок семи разных книг. Имеется P7=7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг. Обсуждение.Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно. Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов). Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны. И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере. Пример.На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек? Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числасочетанийиз 20 элементов по 5. Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок, которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5. Задачи для самопроверки 1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться? 2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево? 3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день? 4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек? 5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо? 6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать? 4. Вероятность события. Классическое определение Вероятность события количественно характеризует возможность (шанс) осуществления этого события в ходе случайного эксперимента. В данном параграфе мы начинаем изучать возможности, предоставляемые теорией вероятности для сравнительного анализа ситуаций, возникающих при различных комбинациях равновероятных событий. Представим, что у нас проводится эксперимент с пространством из n элементарных исходов, которые равновероятны. Элементарные исходы являются несовместными событиями (напомним, что несовместные события - это те, которые не могут произойти одновременно), поэтому вероятность каждого из них равна 1/n. Допустим, нас интересует событие А, которое наступает только при реализацииблагоприятных элементарных исходов, количество последнихm(m< n). Тогда, согласно классическому определению, вероятность такого события: Р(А)=m/n. Для любого события А справедливо неравенство:0 < P(A) <1. Пример 1. Лотерея состоит из 1000 билетов, среди них 200 выигрышных. Наугад вынимается один билет из 1000. Чему равна вероятность того, что этот билет выигрышный? Решение: различных исходов в этом примере 1000 (n=1000). В интересующее нас событие А входят 200 исходов (m=200). Таким образом, Пример 2. В коробке лежат 200 белых, 100 красных и 50 зеленых шаров. Наудачу вынимается один шар. Чему равны вероятности получить шар белого, красного или зеленого цвета? Решение: Рассмотрим события: А={вынули белый шар}, В={вынули красный шар}, С={вынули зеленый шар}. n=350, тогда Пример 3. Бросается игральная кость. Чему равны вероятности следующих событий: А={выпала грань с 6 очками}, В={выпала грань с четным числом очков}, С={выпала грань с числом очков, делящимся на 3}? Решение: n=6. Событию А благоприятствует один исход, событию В - три исхода, событию С - два исхода. Таким образом, Иногда в задачах число элементарных исходов бывает так велико, что выписать их все не представляется возможным. Поэтому применяются формулы из комбинаторики (см. §2). Пример 4.Из колоды в 36 карт вытаскивают три. Какова вероятность того, что среди вынутых карт нет десяток? Решение: В этом примере элементарным исходом является случайный набор из трех карт. Общее число элементарных исходов равно N=C363 , элементарные исходы считаем равновозможными. Благоприятных исходов (количество возможных наборов по три карты из той же колоды, но без десяток) m=C323 . Таким образом, вероятность события A {Вынуто 3 карты из 36 и среди них нет десяток}: . Задачи для самопроверки 1. Бросаются одновременно две игральные кости. Найти вероятности следующих событий: А-сумма выпавших очков равна 8; В-произведение выпавших очков равно 8. 2. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется разыскиваемая. 3. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что номер набран правильно. 5. Независимость событий. Последовательные события и слепой случай. Теорема умножения вероятностей. "Дерево вероятностей" При оценки вероятности наступления какого-либо случайного события очень важно предварительно хорошо представлять, зависит ли вероятность наступления интересующего нас события от того, как развиваются остальные события. В случае классической схемы, когда все исходы равновероятны, мы уже можем оценить значения вероятности интересующего нас отдельного события самостоятельно. Мы можем сделать это даже в том случае, если событие является сложной совокупностью нескольких элементарных исходов. А если несколько случайных событий происходит одновременно или последовательно? Как это влияет на вероятность реализации интересующего нас события? Если я несколько раз кидаю игральную кость, и хочу, чтобы выпала "шестерка", а мне все время не везет, значит ли это, что надо увеличивать ставку, потому что, согласно теории вероятностей, мне вот-вот должно повезти? Увы, теория вероятности не утверждает ничего подобного. Ни кости, ни карты, ни монетки не умеют запоминать, что они продемонстрировали нам в прошлый раз. Им совершенно не важно, в первый раз или в десятый раз сегодня я испытываю свою судьбу. Каждый раз, когда я повторяю бросок, я знаю только одно: и на этот раз вероятность выпадения "шестерки" снова равна одной шестой. Конечно, это не значит, что нужная мне цифра не выпадет никогда. Это означает лишь то, что мой проигрыш после первого броска и после любого другого броска - независимые события. События А и В называются независимыми, если реализация одного из них никак не влияет на вероятность другого события. Например, вероятности поражения цели первым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события "первое орудие поразило цель" и "второе орудие поразило цель" независимы. Если два события А и В независимы, и вероятность каждого из них известна, то вероятность одновременного наступления и события А, и события В (обозначается АВ) можно посчитать, воспользовавшись следующей теоремой. Теорема умножения вероятностей для независимых событий: P(AB) = P(A)*P(B) - вероятность одновременного наступления двух независимых событий равна произведениювероятностей этих событий. Пример.Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: р1=0,7; р2=0,8. Найти вероятность попадания при одном залпе обоими орудиями одновременно. Решение: как мы уже видели события А (попадание первого орудия) и В (попадание второго орудия) независимы, т.е. Р(АВ)=Р(А)*Р(В)=р1*р2=0,56. Что произойдет, с нашими оценками, если исходные события не являются независимыми? Давайте немного изменим предыдущий пример. Пример.Два стрелка на соревнованиях стреляют по мишеням, причем, если один из них стреляет метко, то соперник начинает нервничать, и его результаты ухудшаются. Как превратить эту житейскую ситуацию в математическую задачу и наметить пути ее решения? Интуитивно понятно, что надо каким-то образом разделить два варианта развития событий, составить по сути дела два сценария, две разные задачи. В первом случае, если соперник промахнулся, сценарий будет благоприятный для нервного спортсмена и его меткость будет выше. Во втором случае, если соперник прилично реализовал свой шанс, вероятность поразить мишень для второго спортсмена снижается. Для разделения возможных сценариев (их часто называют гипотезами) развития событий мы будем часто использовать схему "дерева вероятностей". Эта схема похожа по смыслу на дерево решений, с которым Вам, наверное, уже приходилось иметь дело. Каждая ветка представляет собой отдельный сценарий развития событий, только теперь она имеет собственное значение так называемой условной вероятности (q1, q2, q1-1, q2-1). Эта схема очень удобна для анализа последовательных случайных событий. Остается выяснить еще один немаловажный вопрос: откуда берутся исходные значения вероятностей вреальных ситуациях? Ведь не с одними же монетами и игральными костями работает теория вероятностей? Обычно эти оценки берутся из статистики, а когда статистические сведения отсутствуют, мы проводим собственное исследование. И начинать его нам часто приходится не со сбора данных, а с вопроса, какие сведения нам вообще нужны. Пример.Допустим, нам надо оценить в городе с населением в сто тысяч жителей объем рынка для нового товара, который не является предметом первой необходимости, например, для бальзама по уходу за окрашенными волосами. Рассмотрим схему "дерева вероятностей". При этом значение вероятности на каждой "ветке" нам надо приблизительно оценить. Итак, наши оценки емкости рынка: 1) из всех жителей города женщин 50%, 2) из всех женщин только 30% красят волосы часто, 3) из них только 10% пользуются бальзамами для окрашенных волос, 4) из них только 10% могут набраться смелости попробовать новый товар, 5) из них 70% обычно покупает все не у нас, а у наших конкурентов. Решение: По закону перемножения вероятностей, определяем вероятность интересующего нас события А={житель города покупает у нас этот новый бальзам}=0,00045. Умножим это значение вероятности на число жителей города. В результате имеем всего 45 потенциальных покупательниц, а если учесть, что одного пузырька этого средства хватает на несколько месяцев, не слишком оживленная получается торговля. И все-таки польза от наших оценок есть. Во-первых, мы можем сравнивать прогнозы разных бизнес-идей, на схемах у них будут разные "развилки", и, конечно, значения вероятности тоже будут разные. Во-вторых, как мы уже говорили, случайная величина не потому называется случайной, что она совсем ни от чего не зависит. Просто ее точное значение заранее не известно. Мы знаем, что среднее количество покупателей может быть увеличено (например, с помощью рекламы нового товара). Так что имеет смысл сосредоточить усилия на тех "развилках", где распределение вероятностей нас особенно не устраивает, на тех факторах, на которые мы в состоянии повлиять. Рассмотрим еще один количественный пример исследования покупательского поведения. Пример.За день продовольственный рынок посещает в среднем 10000 человек. Вероятность того, что посетитель рынка заходит в павильон молочных продуктов, равна 1/2. Известно, что в этом павильоне в среднем продается в день 500 кг различных продуктов. Можно ли утверждать, что средняя покупка в павильоне весит всего 100 г? Обсуждение.Конечно, нельзя. Понятно, что не каждый, кто заходил в павильон, в результате что-то там купил. Как показано на схеме, чтобы ответить на вопрос о среднем весе покупки, мы должны найти ответ на вопрос, какова вероятность того, что человек, зашедший в павильон, что-нибудь там купит. Если таких данных в нашем распоряжении не имеется, а нам они нужны, придется их получить самим, понаблюдав некоторое время за посетителями павильона. Допустим, наши наблюдения показали, что только пятая часть посетителей павильона что-то покупает. Как только эти оценки нами получены, задача становится уже простой. Из 10000 человек, пришедших на рынок, 5000 зайдут в павильон молочных продуктов, покупок будет только 1000. Средний вес покупки равен 500 грамм. Интересно отметить, что для построения полной картины происходящего, логика условных "ветвлений" должна быть определена на каждом этапе нашего рассуждения так же четко, как если бы мы работали с "конкретной" ситуацией, а не с вероятностями. Задачи для самопроверки 1. Пусть есть электрическая цепь, состоящая из n последовательно соединенных элементов, каждый из которых работает независимо от остальных. Известна вероятность p невыхода из строя каждого элемента. Определите вероятность исправной работы всего участка цепи (событие А). 2. Студент знает 20 из 25 экзаменационных вопросов. Найдите вероятность того, что студент знает предложенные ему экзаменатором три вопроса. 3. Производство состоит из четырех последовательных этапов, на каждом из которых работает оборудование, для которого вероятности выхода из строя в течение ближайшего месяца равны соответственно р1, р2, р3 и р4. Найдите вероятность того, что за месяц не случится ни одной остановки производства из-за неисправности оборудования. 6. Статистическое (частотное) определение вероятности. Теорема сложения вероятностей В этом разделе мы начнем применять на практике математический аппарат теории вероятностей для оценки вероятности наступления интересующего нас случайного события, которое, в свою очередь, является некоторой комбинацией других случайных событий. Классическое определение вероятности Р(А) события А как отношения числа благоприятных элементарных исходов m к числу всех элементарных исходов n предполагает, что все элементарные исходыравновероятны. Однако, это условие далеко не всегда выполняется, поэтому мы сейчас введем еще одно определение вероятности -статистическое (или частотное). Как оценить вероятность интересующего нас события, если в процессе испытания элементарные исходы вовсе не обязаны быть равновероятными? Строго говоря, необходимо было бы много раз проделать интересующий нас опыт и узнатьчастоту реализации различных элементарных исходов. В пределе, при увеличении числа испытаний, отношение числаmреализованных событий А к общему количеству испытанийnи будет определять вероятность Р(А)=m/n. Важно понимать, что статистический подход не противоречит классическому, а лишь расширяет границы возможного применения аппарата теории вероятностей. Поэтому все приемы, которые Вы уже освоили в рамках классической схемы, можно будет использовать и в дальнейшем. Для решения практических задач нам понадобятся следующие важные теоремы. 1. Теорема сложения вероятностей для несовместных событий: P(A + B) = P(A) + P(B)- вероятность наступления в результате эксперимента хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий. Обсуждение.Напомним, что события А и В называются несовместными, если в результате опыта они не могут появиться вместе. (Пожалуйста, не путайте их с независимыми событиями, которые мы обсуждали в прошлом разделе. Независимые события могут спокойно сосуществовать друг с другом.) Пример.По статистике, в прошлом году 10% жителей нашего города встретили Новый год в отъезде, 40% ходили в гости или в ресторан, оставаясь в городе, остальные встречали Новый год дома. Считая, что эта тенденция сохранится, посчитайте вероятность того, что житель нашего города встретит Новый год дома. Решение: здесь можно смело пользоваться теоремой сложения вероятностей, т.к. события встречи Нового года в разных местах одним и тем же человеком - несовместны. Поэтому все, кто встретит Новый год в гостях или в другом городе (они составят вместе 40%+10%), не смогут встретить его дома. Принимая общее число жителей города за 100%, найдем, что 50% оставалось дома в прошлый раз. Полагая, что эти же пропорции сохранятся и в этом году, найдем, что вероятность встретить Новый год дома для жителя нашего города равна Р=0,5. (Заметим, что в данном случае нам было удобно посчитать сначала вероятность обратного события, а потом вычесть результат из 100%.) Что произойдет, с нашими оценками, если исходные события не являются несовместными? Давайте немного изменим предыдущий пример. Пример. Владелец фирмы частных такси хочет сделать прогноз количества клиентов на новогоднюю ночь. Пусть, по его сведениям, в прошлом году Новый год встретили дома 50%, в компании друзей или родственников, но не выезжая из города - 80%, в отъезде были 10%. Почему у него получилось в сумме больше 100%? Видимо, каких-то жителей он посчитал больше одного раза. Скорее всего, тех, кто сидел дома, но, одновременно, принимал друзей или родственников, которые пришли к нему в гости. Поскольку эти события не являются несовместными, просто складывая вероятности, он завышает свои оценки. Впрочем, это относится не только к оценке вероятности события, но и к решению любых задач на подсчет элементов объединения двух множеств путем сложения. Если множества частично перекрываются, сумма их элементов будет больше, чем реальное количество элементов, поскольку при арифметическом сложении элементы этого "перекрытия" мы невольно посчитали дважды, и как входящие в первое множество, и как входящие во второе. Выход здесь один: мы должны заметить, что множества частично "перекрываются", посчитать число элементов в их общей части и вычесть это число из суммы (т.к. при суммировании мы его посчитали дважды). В случае подсчета вероятности события С, которое наступает или при наступлении события А, или при наступлении события В, если А и В не являются несовместными, можно воспользоваться следующей теоремой: 2. Общая теорема сложения вероятностей: Р(С)=Р(А)+Р(В)-Р(АВ), где Р(АВ) - вероятность одновременного наступления и события А, и события В. Вопросы для самопроверки 1. Из колоды в 36 карт наудачу вынимается одна. Какова вероятность того, что будет вынута пика или дама? 2. На полке стоят 15 книг, из них пять в переплете. Наудачу берут три книги. Найти вероятность того, что хотя бы одна из взятых книг в переплете (событие А). 7. Формула полной вероятности В данном разделе мы рассмотрим более сложные задачи, имеющие большое практическое значение. Эти задачи встречается на практике в случае, если имеются несколько возможных сценариев развития событий (несколько вероятных гипотез). Известны как величины вероятности реализации каждого из сценариев, так и вероятность наступления интересующего нас события для любого из этих сценариев, а нас интересует, какова полная (совокупная) вероятность наступления интересующего нас события. Предположим, что в результате опыта может произойти одно из n несовместных событий (гипотез) Н1, H2, ..., Hn. Пусть также имеется некоторое событие А и известны Р(Нi) - вероятность гипотезы, P(A!Hi) - условная вероятность события А при этой гипотезе). Тогда вероятность события А вычисляется по формуле полной вероятности: Пример. Из 40 деталей 10 изготовлены в первом цехе, 25 - во втором, а остальные - в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех - с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества? Решение: обозначим событие А={выбрана деталь отличного качества}, Hi={выбранная деталь изготовлена в i цехе}, i=1, 2, 3. Тогда По условию задачи P(A!H1) = P(A!H3) = 0,9, P(A!H2)=0,7 По формуле полной вероятности находим искомую вероятность: Пример. На рисунке изображена схема дорог. Найти вероятность того, что турист, вышедший из пункта А, попадет в пункт В, если на развилке он наугад выбирает любую дорогу (кроме обратной). Решение: Обозначим Hi={приход туриста в пункт Hi}, i=1, 2, 3, 4. Поскольку, выйдя из пункта А, он выбирает любую дорогу наугад, то P(Hi)=1/4, i=1, 2, 3, 4. Исходя из схемы дорог, определяем, что P(B!H1) = 0; P(B!H2) =1/2; P(B!H3) = 1; P(B!H4) =1/3 Таким образом, по формуле полной вероятности Пример.Из двенадцати лотерейных билетов пять выигрышных. Билеты вытягиваются по одному без возвращения. Какова вероятность того, что во второй раз вытянут выигрышный билет Решение: Как обычно, вдоль каждой ветви "дерева вероятностей" значения вероятностей перемножаются, а затем значения на концах нужных веток между собой складываются. В результате получаем ответ: После этого раздела Вам нужно выполнить первое письменное задание. Пожалуйста, пишите решение подробно, поясняйте все сделанные Вами предположения. ЗАДАНИЕ 1 В отделе найма персонала проводится тестирование на вакантную руководящую должность. Тест составлен из двух производственных ситуаций, не связанных между собой логически. По каждой ситуации предлагается три примера дальнейших действий, из которых надо выбрать один наилучший. Вероятность того, что претендент знает ответ на первую часть теста равна Р1, вероятность того, что он знает ответ на вторую часть равна Р2. Допустим, что в случае, когда претендент не знает ответа, он принимает решение произвольно выбирать из трех предлагаемых вариантов наугад. Нарисуйте дерево вероятностей и посчитаете вероятности для разных сценариев развития событий. Прокомментируйте свои оценки. Какова вероятность того, что испытуемый знает ответы на обе части теста? Какова полная вероятность, что испытуемый ответит правильно на обе части теста? Можете ли Вы предложить свои способы повышения достоверности результатов такого тестирования? 7. Формула полной вероятности В данном разделе мы рассмотрим более сложные задачи, имеющие большое практическое значение. Эти задачи встречается на практике в случае, если имеются несколько возможных сценариев развития событий (несколько вероятных гипотез). Известны как величины вероятности реализации каждого из сценариев, так и вероятность наступления интересующего нас события для любого из этих сценариев, а нас интересует, какова полная (совокупная) вероятность наступления интересующего нас события. Предположим, что в результате опыта может произойти одно из n несовместных событий (гипотез) Н1, H2, ..., Hn. Пусть также имеется некоторое событие А и известны Р(Нi) - вероятность гипотезы, P(A!Hi) - условная вероятность события А при этой гипотезе). Тогда вероятность события А вычисляется по формуле полной вероятности: Пример. Из 40 деталей 10 изготовлены в первом цехе, 25 - во втором, а остальные - в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех - с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества? Решение: обозначим событие А={выбрана деталь отличного качества}, Hi={выбранная деталь изготовлена в i цехе}, i=1, 2, 3. Тогда По условию задачи P(A!H1) = P(A!H3) = 0,9, P(A!H2)=0,7 По формуле полной вероятности находим искомую вероятность: Пример. На рисунке изображена схема дорог. Найти вероятность того, что турист, вышедший из пункта А, попадет в пункт В, если на развилке он наугад выбирает любую дорогу (кроме обратной). Решение: Обозначим Hi={приход туриста в пункт Hi}, i=1, 2, 3, 4. Поскольку, выйдя из пункта А, он выбирает любую дорогу наугад, то P(Hi)=1/4, i=1, 2, 3, 4. Исходя из схемы дорог, определяем, что P(B!H1) = 0; P(B!H2) =1/2; P(B!H3) = 1; P(B!H4) =1/3 Таким образом, по формуле полной вероятности Пример.Из двенадцати лотерейных билетов пять выигрышных. Билеты вытягиваются по одному без возвращения. Какова вероятность того, что во второй раз вытянут выигрышный билет Решение: Как обычно, вдоль каждой ветви "дерева вероятностей" значения вероятностей перемножаются, а затем значения на концах нужных веток между собой складываются. В результате получаем ответ: После этого раздела Вам нужно выполнить первое письменное задание. Пожалуйста, пишите решение подробно, поясняйте все сделанные Вами предположения. ЗАДАНИЕ 1 В отделе найма персонала проводится тестирование на вакантную руководящую должность. Тест составлен из двух производственных ситуаций, не связанных между собой логически. По каждой ситуации предлагается три примера дальнейших действий, из которых надо выбрать один наилучший. Вероятность того, что претендент знает ответ на первую часть теста равна Р1, вероятность того, что он знает ответ на вторую часть равна Р2. Допустим, что в случае, когда претендент не знает ответа, он принимает решение произвольно выбирать из трех предлагаемых вариантов наугад. Нарисуйте дерево вероятностей и посчитаете вероятности для разных сценариев развития событий. Прокомментируйте свои оценки. Какова вероятность того, что испытуемый знает ответы на обе части теста? Какова полная вероятность, что испытуемый ответит правильно на обе части теста? Можете ли Вы предложить свои способы повышения достоверности результатов такого тестирования? 8. Последовательтность испытаний (схема Бернулли) Практические задачи, связанные с оценкой вероятности наступления события в результате нескольких равноценных попыток могут анализироваться с применением формулы Бернулли или (при большом количестве таких попыток) с применением приближенной формулы Пуассона. Для работы с этим материалом Вам снова потребуется знание основ комбинаторики (Раздел 1.2). Схема Бернулли состоит в следующем: производится последовательность испытаний, в каждом из которых вероятность наступления определенного события А одна и та же и равна р. Испытания предполагаются независимыми (т.е. считается, что вероятность появления события А в каждом из испытаний не зависит от того, появилось или не появилось это событие в других испытаниях). Наступление события А обычно называют успехом, а ненаступление - неудачей. Обозначим вероятность неудачи q=1-P(A)=(1-p). Вероятность того, что в n независимых испытаниях успех наступит ровно m раз, выражается формулой Бернулли: Вероятность Рn(m) при данном n сначала увеличивается при увеличении m от 0 до некоторого значения m0, а затем уменьшается при изменении m от m0 до n. Поэтому m0, называют наивероятнейшим числом наступлений успеха в опытах. Это число m0, заключено между числами np-q и np+p (или, что то же самое, между числами n(p+1)-1 и n(p+1)) .Если число np-q - целое число, то наивероятнейших чисел два: np-q и np+p. Важное замечание.Если np-q< 0, то наивероятнейшее число выигрышей равно нулю. Пример. Игральная кость бросается 4 раза. При каждом броске нас интересует событие А={выпала шестерка}. Решение: Здесь четыре испытания, и т.к. кубик симметричен, то p=P(A)=1/6, q=1-p=5/6. Вероятность того, что в 4 независимых испытаниях успех наступит ровно m раз (m < 4), выражается формулой Бернулли: Посчитаем эти значения и запишем их в таблицу. Самое вероятное число успехов в нашем случае m0=0. Пример.Вероятность появления успеха равна 3/5. Найти наивероятнейшее число наступлений успеха, если число испытаний равно 19, 20. Решение: при n =19 находим Таким образом, максимальная вероятность достигается для двух значений m0, равных 11 и 12. Эта вероятность равна P19(11)=P19(12)=0,1797. При n=20 максимальная вероятность достигается только для одного значения m0, т.к. не является целым числом. Наивероятнейшее число наступлений успеха m0 равно 12. Вероятность его появления равна P20(12)=0,1797. Совпадение чисел P20(12) и P19(12) вызвано лишь сочетанием значений n и p и не имеет общего характера. На практике в случае, когда n велико, а p мало (обычно p < 0,1; npq < 10) вместо формулы Бернулли применяют приближеннуюформулу Пуассона Пример 4.Радиоаппаратура состоит из 1000 элементов. Вероятность отказа одного элемента в течение года равна 0,002. Какова вероятность отказа двух элементов за год? Какова вероятность отказа не менее двух элементов за год? Решение: будем рассматривать работу каждого элемента как отдельное испытание. Обозначим А={отказ элемента за год}. P(A)=p=0,002, l=np=1000*0,002=2< br> По формуле Пуассона Обозначим через P1000( > 2) вероятность отказа не менее двух элементов за год. Переходя к противоположному событию, вычислим P1000( > 2) как: Задачи для самопроверки 1. В семье пять детей. Считая вероятность рождения мальчика и девочки равными 1/2, определить вероятность того, что среди этих детей два мальчика. 3. Наладчик обслуживает 50 станков. Вероятность того, что в течение смены станок потребует регулировки, равна 1/3. Что более вероятно: а) регулировки потребуют 17 станков; б) регулировки потребуют 16 станков? 4. Какова вероятность того, что среди 500 наугад выбранных человек двое родились 1 апреля? 5. Среди 2000 человек приблизительно 16 левшей. Какова вероятность того, что среди сотни наугад выбранных человек окажется хотя бы один левша? 1. Среднее арифметическое, мода и медиана. Среднее квадратическое отклонение Вероятно, Вы отлично знаете, что такое среднее арифметическое. Если мы имеем набор каких-то величин, и все они одной природы (усреднять килограммы с километрами мы, конечно, не можем), надо посчитать сумму, а затем, поделив ее на количество слагаемых, найти среднее арифметическое. Казалось бы, простое и хорошо знакомое действие, но и тут имеется несколько проблем для обсуждения. При знакомстве с некоторыми "показателями" поневоле вспоминается известная шутка о "средней температуре по больнице". Пример.Допустим, фирма имеет две палатки, торгующие горячей выпечкой, которую они пекут на месте из полуфабрикатов. В таблице приводится примерная сводка ежедневной выручки каждой из палаток за неделю (в руб.). Различие в ежедневной выручке в основном связано с расположением палаток. Палатка 1 находится в парке отдыха, в то время как Палатка 2 расположена напротив школы и вблизи проходной крупного НИИ. Владелец фирмы решил выплачивать ежемесячную премию продавцам той палатки, которая даст в этом месяце большую выручку. При распределении премии выяснилась удивительная вещь: выигрыш в этом "соревновании" зависел только от количества выходных в месяце. Не хотелось бы приводить большое количество цифр за весь месяц в целом, но и без этого видно, что если бы владельцу фирмы пришла в голову идея ежедневного премирования победителя какой-то фиксированной суммой, "Палатка выходного дня" могла бы рассчитывать на премии в два с половиной раза реже, хотя недельная выручка от нее больше. В таких условиях более разумное соревнование могло бы быть основано на осреднении показателей за неделю. Допустим, недельные показатели практически совпали. Как оценить, какая из палаток полезнее для фирмы, если по каким-то причинам фирме необходимо продать одну из них? Если выручка практически совпадает, владелец, по-видимому, поинтересуется стабильностью работы торговой точки. Вины продавцов в этом нет, но если оборудование работает два дня в неделю на износ, а в остальное время больше простоев, выход из строя такого оборудования более вероятен. Пусть в один (случайным образом выпавший) день в неделю идет сильный дождь, и на улицах мало прохожих, падение выручки особенно резко заметно, когда такой дождливый день совпадает с одним из выходных. Для сравнения можно представить спортсменов, которые имеют равные шансы выиграть, но один из них выступает ровнее. Скорее всего, именно он и будет принят в состав сборной. Но вот еще один вопрос: а не делает ли эта самая нестабильная палатка работу фирмы в целом более стабильной, прекрасно дополняя работу палатки 2? Давайте выдвинем это утверждение в качестве гипотезы и попробуем его доказать или опровергнуть. Чтобы оценить эту проблему количественно, надо прежде всего просуммировать дневную выручку обеих палаток. То, что мы описали общими словами как "нестабильность работы", в статистике называется характеристикой рассеивания. К ним относятся такие показатели как дисперсия и среднее квадратическое отклонение. Покажем на предыдущем примере, как определяются эти понятия. Посчитаем сначала среднее арифметическое выручки для каждой палатки отдельно, и для обеих палаток вместе (осреднение проводим за семь дней): Хср.1=600 руб., Хср.2=598 руб., Хср.1+2=1198 руб. Чтобы сравнить разброс значений, посчитаем для обеих палаток дневные отклонения выручки от их собственного среднего значения. Чтобы измерить, насколько одна палатка "нестабильнее" другой, хочется сложить всю строку за неделю и получить общее отклонение за весь отчетный период. Но этого делать нельзя, мы сами так построили эти показатели, что, сложив, получим ноль (с точностью до погрешности округления - среднее арифметическое величина не обязательно целая). Чтобы избежать этого обнуления, нам надо, чтобы каждое отклонение от среднего арифметического "лишилось" своего знака. Для этого возводят каждую величину в квадрат, и лишь затем суммируют весь ряд значений. Чтобы не зависеть от периода осреднения делят полученную сумму квадратов на число слагаемых (в нашем случае, по-прежнему на семь). Такая величина называетсядисперсией. Мы видим, что дисперсия действительно очень показательная величина. У "Палатки выходного дня" она выше более, чем в десять раз. Дисперсию можно посчитать в Excel автоматически, даже не считая предварительно среднее арифметическое, программа сделает это сама. Для этого, находясь в файле Excel, нажмите в верхнем меню кнопку fx. Затем, выберите среди функций тип "СТАТИСТИЧЕСКИЕ", и из предложенного перечня в окошке - ДИСПРА. Затем, по подсказке, поставив курсор в поле "Число 1" проведите мышью вдоль строки с набранными значениями. Этот вид подсчета называется "вычисление смещенной дисперсии по генеральной совокупности". Дисперсией часто пользуются, но более удобная характеристика носит название среднее квадратическое отклонение (обычно обозначается греческой буквой омега. Среднее квадратическое отклонение - это квадратный корень из дисперсии, он удобен тем, что имеет ту же размерность, что и исходные величины. Так, в нашем случае, дисперсия имела бы размерность "рубли в квадрате", в то время как среднее квадратическое отклонение получается просто и привычно, в рублях. В нашем примере, видно, что суммарная дисперсия и среднее квадратическое отклонение у двух палаток вместе все-таки выше, чем у одной первой палатки, причем среднее квадратическое отклонение выше более, чем в два раза. Значит, наша гипотеза о "повышенной стабильности суммы" за счет присутствия второй палатки несостоятельна. Иногда, вместо среднего арифметического употребляют другие характерные величины, если это по каким-то причинам лучше описывает выборку. Так если расставить выборку по возрастанию (или убыванию) той величины, которой мы интересуемся, то медиана - это то, что будет ровно посередине "строя". Например, если мы расположим по порядку длительности интервалы времени: секунда, минута, час, сутки и неделя - то медианой будет час. Еще одно понятие для замены среднего -мода. Само название позволяет легко запомнить это определение. Если мы выстроим по порядку все пары обуви на складе по размеру, то самый ходовой размер будет модой. Мода - это то, что непременно должны учитывать производители упаковок и фасовщики. Если бы большинство людей покупало за один раз стакан молока, молочные пакеты не были бы литровыми. В следующем параграфе мы начнем работать со случайными величинами, имеющими нормальное распределение, и эти понятия нам снова встретятся.
|
|
|
|
|
|
|
|
|
|
|
|
Нормальное распределение и его свойства
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход, и т.п., а потом построить график любой из этих величин, например, роста...
Но не будем спешить, сначала посмотрим, как можно построить такой график. Сначала, мы просто запишем результаты своего исследования. Потом, мы отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, "от 180 до 181 включительно". После этого мы должны посчитать количество людей в каждой подгруппе-диапазоне, это будет частота попадания роста жителей города в данный диапазон. Обычно эту часть удобно оформить в виде таблички. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить так называемую гистограмму, упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а длина будет равна той частоте, которая соответствует каждому диапазону роста. Если Вам попалось достаточно много жителей, то Ваша схема будет выглядеть примерно так:

Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, "оплывет" вниз, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Чтобы избежать этого, просто увеличим масштаб по вертикальной оси в 10 раз. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться та знаменитая колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения. В результате, относительная частота встречаемости каждого конкретного диапазона роста может быть посчитана как отношение площади "ломтика" кривой, приходящегося на этот диапазон к площади подо всей кривой. Стандартизарованные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что, как Вы помните из курса теории вероятности, вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста - достоверное событие.
А вот вероятность того, что рост произвольного человека попадет в определенный выбранный нами диапазон, будет зависеть от трех факторов.
Во-первых,от величины такого диапазона - чем точнее наши требования, тем меньше вероятности, что нам повезет.
Во-вторых,от того, насколько "популярен" выбранный нами рост. Напомним, что мода - самое часто встречающееся значение роста. Кстати для нормального распределения мода, медиана и среднее значение совпадают. Кривая нормального распределения симметрична относительно среднего значения. И, в-третьих,вероятность попадания роста в определенный диапазон зависит от характеристики рассеивания случайной величины. Отчасти это связано с единицами измерения (представьте, что мы бы измеряли людей в дюймах, а не в миллиметрах, но сами люди и их рост были бы теми же). Но дело не только в этом. Просто некоторые процессы кучнее группируются возле среднего значения, в то время как другие более разбросаны. Например, рост собак и рост домашних кошек имеют разный разброс значений, их кривые нормального распределения будут выглядеть по-разному (напомним еще раз, что площадь под обеими кривыми будет единичной). Так, кривая для роста кошек будет более узкой и высокой, а для роста собак кривая будет ниже и шире.
Для характеристики разброса конечного ряда данных в прошлом разделе мы использовали величину среднего квадратического отклонения. Аналогичная величина используется для характеристики кривой нормального распределения. Она обозначается буквой s и называется в этом случае стандартным отклонением.
Это очень важная величина для кривой нормального распределения. Кривая нормального распределения полностью задана, если известно среднее значение Хср. и отклонение s.
Кроме того, любой житель города с вероятностью 68% попадет в диапазон роста Х ср.± s, с вероятностью 95% - в диапазон Х ср.± 2s, и с вероятностью 99,7% - в диапазон Х ср.± 3s.
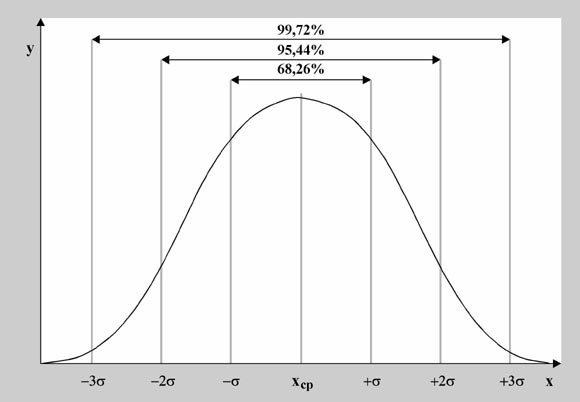
Для вычисления других значений вероятности, которые могут Вам понадобиться, можно воспользоваться приведенной таблицей:
Таблица вероятности попадания случайной величины в отмеченный
(заштрихованный) диапазон

После этого раздела Вам нужно будет выполнить второе письменное задание.
ЗАДАНИЕ 2
В городе модельное агентство приглашает на работу красивых девушек от 18 до 25 лет, имеющих рост не ниже 1,75 метра, с местной пропиской.
Можно считать, что распределение роста и возраста среди жителей города подчиняется нормальному закону. Средний рост женщин данной возрастной категории считайте равным 166 см, отклонение 5 см. Средний возраст 33 года, отклонение 14 лет.
Вероятность того, что девушка красива, составляет 10%.
Нарисуйте дерево вероятностей и ответьте, пожалуйста, на следующие вопросы:
Дата добавления: 2018-05-13; просмотров: 534; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
