ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Основные формулы по предмету физика
КИНЕМАТИКА
• Положение материальной точки в пространстве задается радиусом-векторомг:
 |
где i, j, k — единичные векторы направлений (орты); х, у, z — координаты точки.
Кинематические уравнения движения в координатной форме:


где t — время.
• Средняя скорость

где — перемещение материальной точки за интервал времени
— перемещение материальной точки за интервал времени .
.
Средняя путевая * скорость

где  — путь, пройденный точкой за интервал времени
— путь, пройденный точкой за интервал времени .
.
Мгновенная скорость

где  — проекции скорости v на оси координат.
— проекции скорости v на оси координат.
Модуль скорости

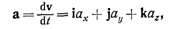 • Ускорение
• Ускорение

где проекции ускорения a на оси
координат.
· См. об этом термине, например, в кн.: Детлаф А. А. и др. Курс физики. М., 1973. Т. I. С. 17.
Модуль ускорения

|
|
При криволинейном движении ускорение можно представить как сумму нормальной  и тангенциальной
и тангенциальной  составляющих (рис.1.1):
составляющих (рис.1.1):

Модули этих ускорений:

где R — радиус кривизны в данной точке траектории.
• Кинематическое уравнение равномерного движения материальной точки вдоль оси х

где  — начальная координата; t — время. При равномерном движении
— начальная координата; t — время. При равномерном движении
v=const и a=0.
• Кинематическое уравнение равнопеременного движения(  )вдоль оси x
)вдоль оси x

где v0 —начальная скорость;t— время.
Скорость точки при равнопеременном движении
v=v0+at.
• Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением)  .
.
|
|
|
Кинематическое уравнение вращательного движения

• Средняя угловая скорость

где 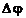 — изменение угла поворота за интервал времени
— изменение угла поворота за интервал времени  . Мгновенная угловая скорость *
. Мгновенная угловая скорость *

• Угловое ускорение *

• Кинематическое уравнение равномерного вращения

где  —начальное угловое перемещение;t—время. При равномерном вращении
—начальное угловое перемещение;t—время. При равномерном вращении  =const и
=const и  =0.
=0.
* Угловая скорость и угловое ускорение являются аксиальными векторами, их направления совпадают с осью вращения.
Частота вращения
n=N/t, или n=1/T,
гдеN — число оборотов, совершаемых телом за время t; Т — период вращения (время одного полного оборота).
• Кинематическое уравнение равнопеременного вращения (  = const.)
= const.)

где  —начальная угловая скорость;t—время.
—начальная угловая скорость;t—время.
Угловая скорость тела при равнопеременном вращении
 .
.
• Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами:
путь, пройденный точкой по дуге окружности радиусом R,
s=  R (
R (  — угол поворота тела);
— угол поворота тела);
скорость точки линейная

ускорение точки:
тангенциальное

нормальное

ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ТЕЛА, ДВИЖУЩИХСЯ ПОСТУПАТЕЛЬНО
Уравнение движения материальной точки (второй закон Ньютона):
в векторной форме
|
|
|
 или
или 
где  — геометрическая сумма сил, действующих на материальную точку; т — масса; а — ускорение;p=mv — импульс; N — число сил, действующих на точку;
— геометрическая сумма сил, действующих на материальную точку; т — масса; а — ускорение;p=mv — импульс; N — число сил, действующих на точку;
в координатной форме (скалярной)
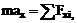

 или
или  ,
,  ,
, 
где под знаком суммы стоят проекции силFi, на соответствующие оси координат.
• Сила упругости *
Fупр=-kx,
где k — коэффициент упругости (жесткость в случае пружины);
х — абсолютная деформация.
 Сила гравитационного взаимодействия *
Сила гравитационного взаимодействия *

где G — гравитационная постоянная; m1 и m2 — массы взаимодействующих тел, рассматриваемые как материальные точки; r — расстояние между ними.
 Сила трения скольжения
Сила трения скольжения
Fтр=fN,
гдеf — коэффициент трения скольжения;N — сила нормального давления.
• Координаты центра масс системы материальных точек
 ,
,  ,
, 
где mi — масса i-й материальной точки; xi,yi;,zi; — ее координаты.
• Закон сохранения импульса
 или
или 
гдеN — число материальных точек (или тел), входящих в систему.
• Работа, совершаемая постоянной силой,
 , или
, или  ,
,
где  — угол между направлениями векторов силы F и перемещения
— угол между направлениями векторов силы F и перемещения  r.
r.
• Работа, совершаемая переменной силой,

где интегрирование ведется вдоль траектории, обозначаемойL.
• Средняя мощность за интервал времени  t
t
 .
.
• Мгновенная мощность
|
|
|
 ,или N=Fvcos
,или N=Fvcos  ,
,
где dA — работа, совершаемая за промежуток времени dt.
• Кинетическая энергия материальной точки (или тела), движущейся поступательно,
T=mv2/2, или T=p2/(2m).
• Потенциальная энергия тела и сила, действующая на тело в данной точке поля, связаны соотношением
F= - grad П или  ,
,
гдеi,j, k — единичные векторы (орты). В частном случае, когда
* См. сноску на с. 19.
поле сил обладает сферической симметрией (как, например, гравитационное),

• Потенциальная энергия упругодеформированного тела (сжатой или растянутой пружины)
П=kx2/2.
Потенциальная энергия гравитационного взаимодействия двух материальных точек (или тел) массами m1, и т2, находящихся на расстоянии r друг от друга,
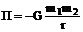
• Потенциальная энергия тела, находящегося в однородном поле силы тяжести,
П=mgh,
где h — высота тела над уровнем, принятым за нулевой для отсчета потенциальной энергии. Эта формула справедлива при условии h<<R, где R — радиус Земли.
• Закон сохранения энергии в механике выполняется в замкнутой системе, в которой действуют только консервативные силы, и записывается в виде
T+П== const.
• Применяя законы сохранения энергии и импульса к прямому центральному удару шаров, получаем формулу скорости абсолютно неупругих шаров после удара
|
|
|
 и формулы скорости абсолютно упругих шаров после удара:
и формулы скорости абсолютно упругих шаров после удара:

где m1 и m2 — массы шаров; v1 и v2 — их скорости до удара.
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
• Момент силыF, действующей на тело, относительно оси вращения
 ,
,
где  — проекция силыF на плоскость, перпендикулярную оси вращения;l — плечо силыF (кратчайшее расстояние от оси вращения до линии действия силы).
— проекция силыF на плоскость, перпендикулярную оси вращения;l — плечо силыF (кратчайшее расстояние от оси вращения до линии действия силы).
• Момент инерции относительно оси вращения:
а) материальной точки
J=mr2,
где т — масса точки; r — расстояние ее от оси вращения;
б) дискретного твердого тела

где  — массаi-го элемента тела;ri — расстояние этого элемента от оси вращения; п — число элементов тела;
— массаi-го элемента тела;ri — расстояние этого элемента от оси вращения; п — число элементов тела;
в) сплошного твердого тела

Если тело однородно, т. е. его плотность  одинакова по всему объему, то
одинакова по всему объему, то
dm=  dV и
dV и 
гдеV — объем тела.
• Моменты инерции некоторых тел правильной геометрической формы:
| Тело | Ось, относительно которой определяется момент инерции | Формула момента инерции |
| Однородный тонкий стержень массой т и длинойl Тонкое кольцо, обруч, труба радиусом R и массой т, маховик радиусомR и массой т, распределенной по ободу Круглый однородный диск (цилиндр) радиусомR и массой т Однородный шар массой т и радиусомR | Проходит через центр тяжести стержня перпендикулярно стержню Проходит через конец стержня перпендикулярно стержню Проходит через центр перпендикулярно плоскости основания Проходит через центр диска перпендикулярно плоскости основания Проходит через центр шара | 1/12ml2 1/3ml2 mR2 1/2mR2 2/5mR2 |
•Теорема Штейнера. Момент инерции тела относительно произвольной оси
J=J0+ma2,
где J0 — момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси; а — расстояние между осями; m — масса тела.
• Момент импульса вращающегося тела относительно оси
L=J  .
.
• Закон сохранения момента импульса

где Li — момент импульса i-го тела, входящего в состав системы. Закон сохранения момента импульса для двух взаимодействующих тел
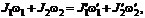
где  — моменты инерции и угловые скорости тел до взаимодействия:
— моменты инерции и угловые скорости тел до взаимодействия:  — те же величины после взаимодействия.
— те же величины после взаимодействия.
Закон сохранения момента импульса для одного тела, момент инерции которого меняется,
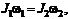
где 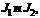 — начальный и конечный моменты инерции;
— начальный и конечный моменты инерции;  —• начальная и конечная угловые скорости тела.
—• начальная и конечная угловые скорости тела.
• Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси
Mdt=d(J  ), где М — момент силы, действующей на тело в течение времени dt;
), где М — момент силы, действующей на тело в течение времени dt;
J — момент инерции тела; — угловая скорость; J
— угловая скорость; J  — момент импульса.
— момент импульса.
Если момент силы и момент инерции постоянны, то это уравнение записывается в виде
М  t=J
t=J  .
.
В случае постоянного момента инерции основное уравнение динамики вращательного движения принимает вид
M=J  , где
, где  — угловое ускорение.
— угловое ускорение.
• Работа постоянного момента силы М, действующего на вращающееся тело,
A=Mj,
где j — угол поворота тела.
• Мгновенная мощность, развиваемая при вращении тела,
N=M  .
.
• Кинетическая энергия вращающегося тела
T=1/2J 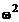 .
.
• Кинетическая энергия тела, катящегося по плоскости без скольжения,
T==1/2mv2+l/2J 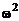 ,
,
гдеl/2mv2 — кинетическая энергия поступательного движения тела; v — скорость центра инерции тела; l/2J 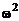 ,— кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр инерции.
,— кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр инерции.
• Работа, совершаемая при вращении тела, и изменение кинетической энергии его связаны соотношением
 .
.
• Величины, характеризующие динамику вращательного движения, и формулы, описывающие это движение, аналогичны соответствующим величинам и формулам поступательного движения.
Эта аналогия раскрывается следующей таблицей:

 Поступательное движение Вращательное движение
Поступательное движение Вращательное движение
 |
Основной закон динамики
F  t=mv2—mv1; M
t=mv2—mv1; M  t=J
t=J  —J
—J  ;
;
F = та М = .J 
Закон сохранения
импульса момента импульса


Работа и мощность
A=Fs; А=М  ,
,
N=FvN=M 
Кинетическая энергия
 Т =1/2mv2T=1/2J
Т =1/2mv2T=1/2J 
СИЛЫ В МЕХАНИКЕ
• Закон всемирного тяготения
 где F — сила взаимного притяжения двух материальных точек; m1 и m2 — их массы; r — расстояние между точками; G — гравитационная постоянная.
где F — сила взаимного притяжения двух материальных точек; m1 и m2 — их массы; r — расстояние между точками; G — гравитационная постоянная.
В написанной форме закон всемирного тяготения можно применять и к взаимодействию шаров, масса которых распределена сферически-симметрично. В этом случае r есть расстояние между центрами масс шаров.
• Напряженность гравитационного поля
 где F — сила тяготения, действующая на материальную точку массы m, помещенную в некоторую точку поля.
где F — сила тяготения, действующая на материальную точку массы m, помещенную в некоторую точку поля.
• Напряженность гравитационного поля, создаваемого планетой, массу М которой можно считать распределенной сферически-симметрично,
 где r — расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.
где r — расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.
• Ускорение свободного падения на высоте h над поверхностью Земли
 где R — радиус Земли; g — ускорение свободного падения на поверхности Земли. Если
где R — радиус Земли; g — ускорение свободного падения на поверхности Земли. Если  , то
, то

• Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m1 и m2 (шаров с массой, распределенной сферически симметрично), находящихся на расстоянии r друг от друга,

(Потенциальная энергия бесконечно удаленных друг от друга материальных точек принята равной нулю.)
• Потенциал гравитационного поля
 где П — потенциальная энергия материальной точки массой m, помещенной в данную точку поля.
где П — потенциальная энергия материальной точки массой m, помещенной в данную точку поля.
• Потенциал гравитационного поля, создаваемого планетой, массу М которой можно считать распределенной сферически-симметрично,
 где r — расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.
где r — расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.
• Законы Кеплера.
1. Планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.
2. Радиус-вектор планеты в равные времена описывает одинаковые площади.
3. Квадраты периодов обращения любых двух планет относятся как кубы больших полуосей их орбит:

Законы Кеплера справедливы также для движения спутников вокруг планеты.
• Относительная деформация при продольном растяжении или сжатии тела
 где ε — относительное удлинение (сжатие); x — абсолютное удлинение (рис. 4.1); l — начальная длина тела.
где ε — относительное удлинение (сжатие); x — абсолютное удлинение (рис. 4.1); l — начальная длина тела.
 |
Относительная деформация при сдвиге определяется из формулы

|
|
Рис. 4.1 Рис. 4.2
где  — относительный сдвиг; Δs — абсолютный сдвиг параллельных слоев тела относительно друг друга (рис. 4.2); h — расстояние между- слоями;
— относительный сдвиг; Δs — абсолютный сдвиг параллельных слоев тела относительно друг друга (рис. 4.2); h — расстояние между- слоями; 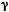 — угол сдвига. (Для малых углов
— угол сдвига. (Для малых углов  )
)
• Напряжение нормальное
 где Fynp — упругая сила, перпендикулярная поперечному сечению тела; S — площадь этого сечения.
где Fynp — упругая сила, перпендикулярная поперечному сечению тела; S — площадь этого сечения.
Напряжение тангенциальное 
где Fynp — упругая сила, действующая вдоль слоя тела; S — площадь этого слоя.
• Закон Гука для продольного растяжения или сжатия
 или
или  ,где k — коэффициент упругости (в случае пружины — жесткость); Е — модуль Юнга.
,где k — коэффициент упругости (в случае пружины — жесткость); Е — модуль Юнга.
Закон Гука для сдвига
 , или
, или  ,где G — модуль поперечной упругости (модуль сдвига).
,где G — модуль поперечной упругости (модуль сдвига).
• Момент, закручивающий на угол φ однородный круглый стержень,
 ,
,
где С — постоянная кручения.
• Работа, совершаемая при деформации тела,

• Потенциальная энергия растянутого или сжатого стержня
 , или
, или  , или
, или  ,где V — объем тела.
,где V — объем тела.
РЕЛЯТИВИСТСКАЯ МЕХАНИКА.
Основные формулы
|
|
В специальной теории относительности рассматриваются только инерциальные системы отсчета. Во всех задачах считается, что оси у, у' и z, z' сонаправлены, а относительная скорость υ0 системы координат К' относительно системы К направлена вдоль общей оси хх' (рис. 5.1).
• Релятивистское (лоренцево) сокращение длины стержня

| Рис. 5.1 |
где l0 — длина стержня в системе координат К' ,относительно которой стержень покоится (собственная длина). Стержень параллелен оси х';l—
длина стержня, измеренная в системе К, относительно которой он движется со скоростью υ; с — скорость распространения электромагнитного излучения.
|
|
• Релятивистское замедление хода часов
где Δt0 — интервал времени между двумя событиями, происходящими в одной точке системы K', измеренный по часам этой системы (собственное время движущихся часов); Δt — интервал времени между двумя событиями, измеренный по часам системы K.
• Релятивистское сложение скоростей
 ,
,
где υ' — относительная скорость (скорость тела относительно системы K'); υ0 — переносная скорость (скорость системы K' относительно К), υ0 — абсолютная скорость (скорость тела относительно системы К).
В теории относительности абсолютной скоростью называется скорость тела в системе координат, условно принятой за неподвижную.
• Релятивистская масса
 , ИЛИ
, ИЛИ  ,где т0 — масса покоя; β — скорость частицы, выраженная в долях скорости света
,где т0 — масса покоя; β — скорость частицы, выраженная в долях скорости света 
• Релятивистский импульс
 , или
, или 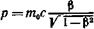
• Полная энергия релятивистской частицы
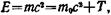
где Т — кинетическая энергия частицы;  — ее энергия покоя. Частица называется релятивистской, если скорость частицы сравнима со скоростью света, и классической, если υ<<с.
— ее энергия покоя. Частица называется релятивистской, если скорость частицы сравнима со скоростью света, и классической, если υ<<с.
• Связь полной энергии с импульсом релятивистской частицы

• Связь кинетической энергии с импульсом релятивистской частицы

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
• Уравнение гармонических колебаний
 где х — смещение колеблющейся точки от положения равновесия;
где х — смещение колеблющейся точки от положения равновесия;
t — время; А, ω, φ— соответственно амплитуда, угловая частота,
начальная фаза колебаний;  — фаза колебаний в момент t.
— фаза колебаний в момент t.
• Угловая частота колебаний
 , или
, или  ,где ν и Т — частота и период колебаний.
,где ν и Т — частота и период колебаний.
• Скорость точки, совершающей гармонические колебания,

• Ускорение при гармоническом колебании

• Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле

где a1и А2— амплитуды составляющих колебаний; φ1 и φ2— их начальные фазы.
• Начальная фаза φ результирующего колебания может быть найдена из формулы

• Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами ν1 и ν2,

• Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами A1 и A2 и начальными фазами φ1 и φ2,

Если начальные фазы φ1и φ2 составляющих колебаний одинаковы, то уравнение траектории принимает вид
 т. е. точка движется по прямой.
т. е. точка движется по прямой.
В том случае, если разность фаз  , уравнение
, уравнение
принимает вид
 т. е. точка движется по эллипсу.
т. е. точка движется по эллипсу.
• Дифференциальное уравнение гармонических колебаний материальной точки
 , или
, или  ,
,
где m — масса точки; k — коэффициент квазиупругой силы (k=тω2).
• Полная энергия материальной точки, совершающей гармонические колебания,

• Период колебаний тела, подвешенного на пружине (пружинный маятник),

где m — масса тела; k — жесткость пружины. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).
Период колебаний математического маятника

где l — длина маятника; g — ускорение свободного падения. Период колебаний физического маятника

где J — момент инерции колеблющегося тела относительно оси
колебаний; а — расстояние центра масс маятника от оси колебаний;
 — приведенная длина физического маятника.
— приведенная длина физического маятника.
Приведенные формулы являются точными для случая бесконечно малых амплитуд. При конечных амплитудах эти формулы дают лишь приближенные результаты. При амплитудах не более  ошибка в значении периода не превышает 1 %.
ошибка в значении периода не превышает 1 %.
Период крутильных колебаний тела, подвешенного на упругой нити,

где J — момент инерции тела относительно оси, совпадающей с упругой нитью; k — жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.
• Дифференциальное уравнение затухающих колебаний
 , или
, или  ,
,
где r — коэффициент сопротивления; δ — коэффициент затухания:  ; ω0— собственная угловая частота колебаний *
; ω0— собственная угловая частота колебаний *

• Уравнение затухающих колебаний

где A (t) — амплитуда затухающих колебаний в момент t; ω — их угловая частота.
• Угловая частота затухающих колебаний

О Зависимость амплитуды затухающих колебаний от времени
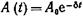 I
I
где А0 — амплитуда колебаний в момент t=0.
• Логарифмический декремент колебаний

где A (t) и A (t+T) — амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.
• Дифференциальное уравнение вынужденных колебаний
 , или
, или
 ,
,
где  — внешняя периодическая сила, действующая на
— внешняя периодическая сила, действующая на
колеблющуюся материальную точку и вызывающая вынужденные
колебания; F0 — ее амплитудное значение; 
• Амплитуда вынужденных колебаний

• Резонансная частота и резонансная амплитуда  и
и 
Дата добавления: 2018-05-12; просмотров: 318; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!




