Варианты индивидуальных заданий
Задание 1
Решить систему уравнений методами Крамера и Гаусса. Сделать проверку полученного решения.
1. 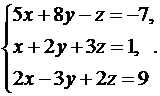 2.
2. 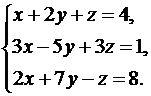
3. 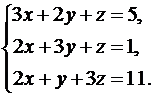 4.
4. 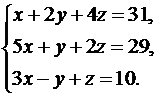
5. 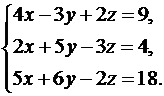 6.
6. 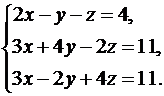
7. 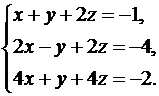 8.
8. 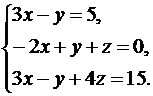
9. 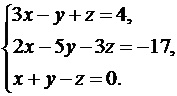 10.
10. 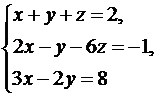
11. 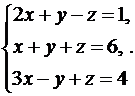 12.
12. 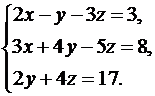
13. 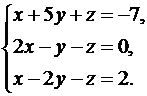 14.
14. 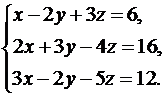
15. 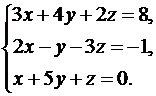 16.
16. 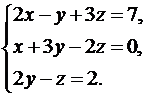
17. 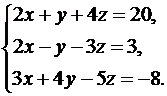 18.
18. 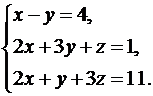
19. 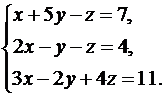 20.
20. 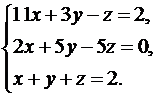
Задание 2
Даны координаты вершин треугольника АВС.
Найти:
1)длину стороны АВ;
2)уравнение стороны АВ и ее угловой коэффициент;
3)уравнение и длину высоты СД;
4)уравнение медианы АЕ;
5)уравнение прямой, проведенной через точку Е, параллельно стороне АВ;
6)сделать чертеж.
1. А(-5;0), В(7;9), С(5;-5). 11. А(-5;2), В(7;-7), С(5;7).
2. А(-7;2),В(5;11),С(3;-3). 12. А(-7;5), В(5;-4), С(3;10).
3. А(-5;-3), В(7;6), С(5;-8). 13. А(-7;1), В(5;-8), С(3;10).
4. А(-6;-2), В(6;7), С(4;-7). 14. А(0;3), В(12;-6), С(10;8).
5. А(-8;-4), В(4;5), С(2;-9). 15. А(-8;4), В(4;-5), С(2;9).
6. А(0;-1), В(12;8), С(10;-6). 16. А(-2;2), В(10;-7), С(8;7).
7. А(-6;1), В(6;10), С(4;-4). 17. А(1;2), В(13;-7), С(11;7).
8. А(-2;-4), В(10;5), С(8;-9). 18. А(-4;1), В(8;-8), С(6;6).
9. А(-3;0), В(9;9), С(7;-5). 19. А(-7;-1), В(5;-10), С(3;4).
10. А(-9;-2), В(3;7), С(1;-7). 20. А(-3;3), В(9;-6), С(7;8).
Задание 3
Даны координаты вершин пирамиды АВСД.
Найти:
1) векторы 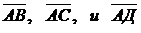 в системе орт и их модули;
в системе орт и их модули;
2) угол между векторами 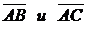 ;
;
3) площадь грани АВС;
4) объем пирамиды АВСД;
5) уравнение ребра АВ;
6) уравнение плоскости АВС;
7) уравнение высоты, опущенной из точки Д на плоскость АВС.
1. А(1;2;1), В(-1;5;1), С(-1;2;7), D(1;5;9).
2. А(2;3;2), В(0;6;2), С(0;3;8), D(2;6;10).
3. А(0;3;2), В(-2;6;2), С(-2;3;8), D(0;6;10).
4. А(2;1;2), В(0;4;2), С(0;1;8), D(2;4;10).
5. А(2;3;0), В(0;6;0), С(0;3;6), D(2;6;8).
6. А(2;2;1), В(0;5;1), С(0;2;7), D(2;5;9).
7. А(1;3;1), В(-1;6;1), С(-1;3;7), D(1;6;9).
8. А(1;2;2), В(-1;5;2), С(-1;2;8), D(1;5;10).
9. А(2;3;1), В(0;6;1), С(0;3;7), D(2;6;9).
10. А(2;2;2), В(0;5;2), С(0;2;8), D(2;5;10).
11. А(1;3;2), В(-1;6;2), С(-1;3;8), D(1;6;10).
12. А(0;1;2), В(-2;4;2), С(-2;1;8), D(0;4;10).
13. А(0;3;0), В(-2;6;0), С(-2;3;6), D(0;6;8).
14. А(2;1;0), В(0;4;0), С(0;1;6), D(2;4;8).
15. А(0;2;1), В(-2;5;1), С(-2;2;7), D(0;5;9).
16. А(1;1;1), В(-1;4;1), С(-1;1;7), D(1;4;9).
17. А(1;2;0), В(-1;5;0), С(-1;2;6), D(1;5;8).
18. А(0;1;0), В(-2;4;0), С(-2;1;6), D(0;4;8).
19. А(0;1;1), В(-2;4;1), С(-2;1;7), D(0;5;9).
20. А(0;2;0), В(-2;5;0), С(-2;2;6), D(0;5;8).
Задание 4
Вычислить пределы:
1. а) 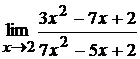 ; б)
; б) 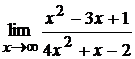 ;
;
в) 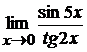 ; г)
; г) 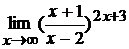 .
.
2. а) 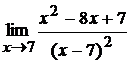 ; б)
; б) 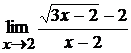 ;
;
в) 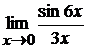 ; г)
; г) 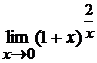 .
.
3. а) 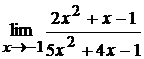 ; б)
; б) 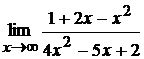 ;
;
в)  ; г)
; г) 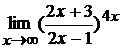 .
.
4. а) 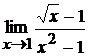 ; б)
; б) 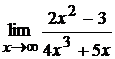 ;
;
в) 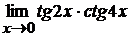 ; г)
; г) 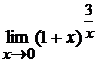 .
.
5. а) 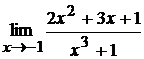 ; б)
; б) 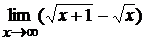 ;
;
в) 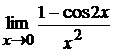 ; г)
; г) 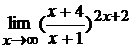 .
.
6. а) 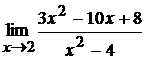 ; б)
; б) 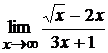 ;
;
в) 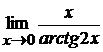 ; г)
; г) 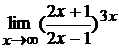 .
.
7. а) 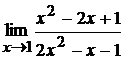 ; б)
; б) 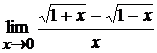 ;
;
в) 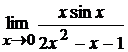 ; г)
; г) 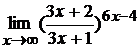 .
.
8. а) 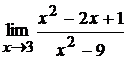 ; б)
; б) 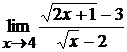 ;
;
в) 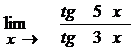 ; г)
; г) 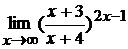 .
.
9. а) 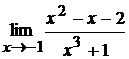 ; б)
; б) 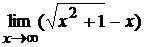 ;
;
в) 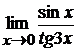 ; г)
; г) 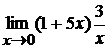 .
.
10. а) 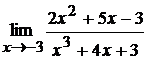 ; б)
; б) 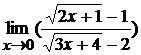 ;
;
в) 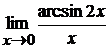 ; г)
; г) 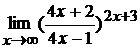 .
.
11. а) 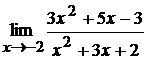 ; б)
; б) 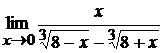 ;
;
в) 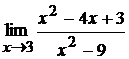 ; г)
; г) 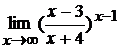 .
.
12. а) 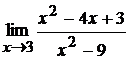 ; б)
; б) 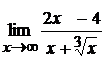 ;
;
в) 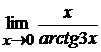 ; г)
; г) 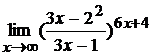 .
.
13. а) 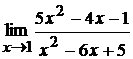 ; б)
; б) 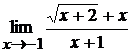 ;
;
в) 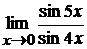 ; г)
; г) 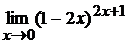 .
.
14. а) 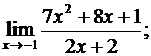 ; б)
; б) 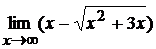 ;
;
в) 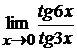 ; г)
; г) 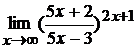 .
.
15. а) 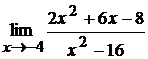 ; б)
; б) 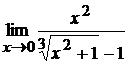 ;
;
в) 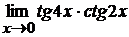 ; г)
; г) 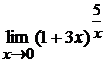 .
.
16. а) 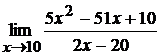 ; б)
; б) 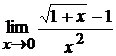 ;
;
в) 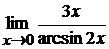 ; г)
; г) 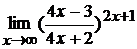 .
.
17. а) 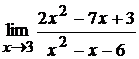 ; б)
; б) 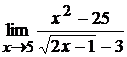 ;
;
в) 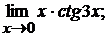 г)
г) 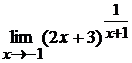 .
.
18. а) 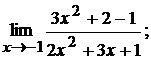 б)
б) 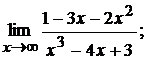
в) 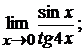 г)
г) 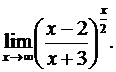
19. а) 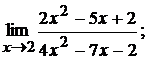 б)
б) 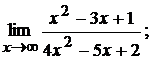
в) 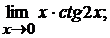 г)
г) 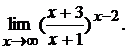
20. а) 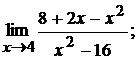 б)
б) 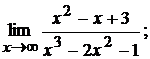
в) 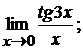 г)
г) 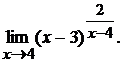
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Письменный Д. Т.
Конспект лекций по высшей математике : полный курс / Д. Т. Письменный . - 9-е изд. - М.: Айрис-Пресс, 2008. – 280с.- Ч. 1.
2. Пискунов Н. С.
Дифференциальное и интегральное исчисления: учеб. пособие для вузов / Н. С. Пискунов. - изд. стер.. - М.: Интеграл-Пресс, 2006. – 415 с. Т.1.
3. Шипачев В.С.
Курс высшей математики: учебник для вузов / В.С.Шипачев; Под редакцией А.Н. Тихонова. – 3-е изд., испр. – М.: Издательство Оникс, 2007 – 600с.: ил.
4. Берман Г. Н.
Сборник задач по курсу математического анализа: учеб. пособие / Г. Н. Берман. - 22-е изд., перераб. - СПб.: Профессия, 2006 - 432 с.
5. Лунгу К.Н.
Сборник задач по высшей математике: учеб. пособие / К.Н.Лунгу и др.- 7-е изд..- М.: Айрис Пресс, 2008.- 574 с.
6. Шипачев В. С.
Задачник по высшей математике: учеб. пособие для вузов / В. С. Шипачев. - 8-е изд., стер. - М.: Высш. шк., 2008. - 304 с.: ил.
7. Данко П. Е.
Высшая математика в упражнениях и задачах: учеб. пособие / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова . - 6-е изд..-М.: ОНИКС.- 2008 .-368 с.- Ч.1.
Дата добавления: 2018-05-12; просмотров: 149; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
