А) Рассмотрим линейную регрессию.
Nbsp; Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» Институт права и управления Кафедра «Финансы и менеджмент»
Методические указания
К контрольно-курсовой работе
по дисциплине«Эконометрика»
Направление подготовки: 38.03.01 «Экономика»
Профили подготовки: «Финансы и кредит», «Бухгалтерский учет, анализ и аудит», «Налоги и налогообложение», «Мировая экономика»
Квалификация (степень) выпускника: 63 бакалавр
Форма обучения: заочная
Тула 2017
Методические указания для ККР рассмотрены и утверждены на заседании кафедры «Финансы и менеджмент» института права и управления,
протокол № _1_ от” _30_” августа_ 2017_г.
Зав. кафедрой __________________________А.Л. Сабинина
В соответствии с учебным планом, студентызаочной формы обучения по дисциплине «Эконометрика» должны выполнить контрольную работу заочника, в которой они должны продемонстрировать свое умение применять знания, полученные на лекционных занятиях и при самостоятельной работе для изучения данного курса.Задача ККР – выработать у студентов твердые навыки исследования и решения определенного круга задач, привить способность к аналитическому мышлению и умению работать со специальной справочной литературой и таблицами.
|
|
|
Задание для ККР
Экономист, изучая зависимость уровня издержек обращения  (тыс. руб.) от объема товарооборота
(тыс. руб.) от объема товарооборота  (тыс. руб.), обследовал 10 магазинов, торгующих одинаковым ассортиментом товаров, и получил следующие данные (таблица 1).
(тыс. руб.), обследовал 10 магазинов, торгующих одинаковым ассортиментом товаров, и получил следующие данные (таблица 1).
Задание: 1.Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнений линейной, степенной и гиперболической регрессии.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4.Дайте с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5.Оцените с помощью средней ошибки аппроксимации качество уравнений регрессии.
6.Оцените с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в п.п. 3-5 и данном пункте, выберите лучшее уравнение регрессии и дайте обоснование этого шага.
7.Для выбранной лучшей модели постройте таблицу дисперсионного анализа и найдите доверительные интервалы для параметров регрессии и коэффициента корреляции.
|
|
|
8. Сделать прогноз значения  при
при  (см. задание) и найти доверительные интервалы прогноза для двух уравнений регрессии
(см. задание) и найти доверительные интервалы прогноза для двух уравнений регрессии
 .
.
9. Оценить полученные результаты и сделать выводы о достоверности и точности прогноза, проверить регрессию на гетероскедастичность, автокорреляцию остатков и выполнение других предпосылок МНК.
Внимание!Номер варианта определяется по двум последним цифрам зачеткиили определяет преподаватель. Если номер более 30, необходимо из номера вычесть число 30 или кратное 30.
Исходные данные для тридцатиодного варианта приведены в табл.1.
Таблица 1.
| № вар-та | № п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | х* | ||
| 1 | Х | 110 | 85 | 70 | 105 | 150 | 90 | 60 | 140 | 100 | 115 | 130 | ||
| У | 6,1 | 4,2 | 2,9 | 5,8 | 8,3 | 5,2 | 3,4 | 7,5 | 4,9 | 5,4 | ||||
| 2 | Х | 80 | 60 | 100 | 130 | 120 | 50 | 90 | 150 | 70 | 125 | 120 | ||
| У | 4,2 | 4,9 | 7,2 | 9,1 | 6,4 | 3,9 | 5,1 | 8,4 | 3,5 | 8,7 | ||||
| 3 | Х | 160 | 120 | 110 | 80 | 90 | 130 | 150 | 70 | 100 | 60 | 130 | ||
| У | 12,5 | 9,3 | 9,2 | 5,1 | 7,5 | 11,6 | 13,1 | 5,2 | 7,9 | 4,4 | ||||
| 4 | Х | 50 | 130 | 100 | 80 | 90 | 70 | 150 | 60 | 140 | 110 | 120 | ||
| У | 4,2 | 10,8 | 9,6 | 6,3 | 7,4 | 6,2 | 11,4 | 3,3 | 12,2 | 10,5 | ||||
| 5 | Х | 60 | 90 | 150 | 65 | 110 | 120 | 70 | 130 | 100 | 140 | 125 | ||
| У | 1,9 | 6,1 | 12,8 | 2,8 | 8,4 | 9,6 | 3,4 | 11,2 | 6,7 | 12,6 | ||||
| 6
| Х | 70 | 110 | 85 | 70 | 100 | 90 | 120 | 80 | 130 | 110 | 140 | ||
| У | 2,8 | 3,5 | 2,4 | 3,6 | 3,4 | 3,2 | 3,6 | 2,5 | 4,1 | 3,3 | ||||
| 7 | Х | 80 | 60 | 100 | 70 | 50 | 110 | 90 | 40 | 75 | 105 | 120 | ||
| У | 4,2 | 4,0 | 4,5 | 3,6 | 3,4 | 5,2 | 3,9 | 3,1 | 3,3 | 4,9 | ||||
| 8 | Х | 100 | 110 | 60 | 120 | 70 | 80 | 130 | 75 | 105 | 50 | 140 | ||
| У | 3,8 | 4,4 | 3,2 | 4,8 | 3,0 | 3,5 | 4,5 | 3,3 | 4,1 | 3,1 | ||||
| 9 | Х | 120 | 85 | 110 | 70 | 115 | 90 | 60 | 55 | 100 | 130 | 125 | ||
| У | 4,0 | 3,6 | 4,0 | 2,6 | 4,3 | 3,4 | 2,9 | 2,5 | 3,0 | 4,5 | ||||
| 10 | Х | 140 | 110 | 120 | 90 | 130 | 80 | 100 | 75 | 135 | 60 | 125 | ||
| У | 5,4 | 4,1 | 5,6 | 3,3 | 4,2 | 2,9 | 3,6 | 2,5 | 4,9 | 3,0 | ||||
| 11 | Х | 115 | 90 | 75 | 110 | 155 | 95 | 65 | 145 | 105 | 120 | 130 | ||
| У | 6,2 | 4,3 | 3,0 | 5,9 | 8,4 | 6,3 | 3,5 | 7,6 | 5,0 | 5,5 | ||||
| 12 | Х | 85 | 65 | 105 | 135 | 125 | 55 | 95 | 155 | 75 | 130 | 120 | ||
| У | 4,3 | 5,0 | 7,3 | 9,2 | 6,5 | 4,0 | 5,2 | 8,5 | 3,6 | 8,8 | ||||
| 13 | Х | 165 | 125 | 115 | 85 | 95 | 135 | 155 | 75 | 105 | 65 | 110 | ||
| У | 12,6 | 9,4 | 9,3 | 5,2 | 7,6 | 11,7 | 13,2 | 5,3 | 8,0 | 4,5 | ||||
| 14 | Х | 55 | 135 | 105 | 85 | 195 | 75 | 155 | 65 | 145 | 115 | 120 | ||
| У | 4,3 | 10,9 | 9,7 | 6,4 | 7,5 | 6,3 | 11,5 | 3,4 | 12,3 | 10,6 | ||||
| 15 | Х | 65 | 95 | 155 | 70 | 105 | 125 | 75 | 135 | 105 | 145 | 140 | ||
| У | 3,0 | 7,2 | 11,9 | 6,4 | 7,3 | 8,5 | 4,9 | 11,3 | 6,8 | 10,7 | ||||
| 16 | Х | 75 | 115 | 90 | 70 | 105 | 95 | 125 | 85 | 135 | 115 | 120 | ||
| У | 2,9 | 3,6 | 2,5 | 2,2 | 3,5 | 3,3 | 3,7 | 2,6 | 4,2 | 3,4 | ||||
| 17 | Х | 85 | 65 | 105 | 75 | 55 | 115 | 95 | 45 | 80 | 110 | 130
| ||
| У | 4,3 | 4,1 | 4,6 | 3,7 | 3,5 | 5,3 | 4,0 | 3,2 | 3,4 | 5,0 | ||||
| 18 | Х | 105 | 115 | 65 | 125 | 75 | 85 | 135 | 80 | 110 | 55 | 140 | ||
| У | 3,9 | 4,5 | 3,3 | 4,9 | 3,1 | 3,6 | 4,6 | 3,4 | 4,2 | 3,2 | ||||
| 19 | Х | 125 | 90 | 115 | 75 | 120 | 95 | 65 | 60 | 105 | 135 | 130 | ||
| У | 4,1 | 3,7 | 4,1 | 2,7 | 4,4 | 3,5 | 3,0 | 2,6 | 3,1 | 4,6 | ||||
| 20 | Х | 145 | 115 | 125 | 95 | 135 | 85 | 105 | 80 | 140 | 65 | 120 | ||
| У | 5,5 | 4,2 | 5,7 | 3,3 | 4,3 | 3,0 | 3,7 | 2,6 | 5,0 | 3,1 | ||||
| 21 | У | 5 | 11 | 15 | 17 | 20 | 22 | 25 | 27 | 30 | 35 | 46 | ||
| Х | 70 | 65 | 55 | 60 | 50 | 35 | 40 | 30 | 25 | 32 | ||||
| 22 | Х | 80 | 60 | 100 | 130 | 120 | 50 | 90 | 150 | 70 | 125 | 105 | ||
| У | 6,0 | 6,3 | 8,2 | 10,1 | 7,4 | 4,9 | 6,1 | 9,4 | 4,5 | 9,7 | ||||
| 23 | У | 5 | 10 | 15 | 20 | 25 | 30 | 25 | 30 | 35 | 40 | 45 | ||
| Х | 60 | 70 | 65 | 60 | 50 | 40 | 30 | 25 | 20 | 30 | ||||
| 24 | Х | 100 | 110 | 60 | 120 | 70 | 80 | 130 | 85 | 110 | 60 | 125 | ||
| У | 2,8 | 4,6 | 3,4 | 4,9 | 3,0 | 3,5 | 4,5 | 3,3 | 4,5 | 3,2 | ||||
| 25 | Х | 105 | 115 | 95 | 85 | 125 | 70 | 115 | 75 | 90 | 135 | 110 | ||
| У | 3,5 | 3,4 | 3,2 | 2,6 | 3,7 | 2,2 | 3,6 | 2,9 | 2,5 | 4,2 | ||||
| 26 | Х | 115 | 100 | 140 | 60 | 90 | 150 | 105 | 70 | 85 | 110 | 130 | ||
| У | 5,4 | 4,8 | 7,6 | 3,5 | 5,3 | 8,2 | 5,7 | 2,9 | 4,3 | 6,2 | ||||
| 27 | Х | 125 | 70 | 150 | 90 | 50 | 120 | 130 | 100 | 60 | 80 | 120 | ||
| У | 8,6 | 3,5 | 8,8 | 5,1 | 3,9 | 7,4 | 9,1 | 7,2 | 4,9 | 4,8 | ||||
| 28 | Х | 60 | 100 | 70 | 150 | 130 | 90 | 80 | 110 | 120 | 160 | 130 | ||
| У | 4,4 | 7,8 | 5,2 | 13,1 | 11,6 | 7,6 | 5,1 | 9,2 | 9,4 | 12,4 | ||||
| 29 | Х | 110 | 140 | 60 | 150 | 70 | 90 | 80 | 100 | 130 | 50 | 120 | ||
| У | 10,5 | 12,2 | 3,3 | 11,4 | 6,2 | 7,4 | 6,3 | 9,6 | 10,8 | 4,2 | ||||
| 30 | Х | 120 | 110 | 90 | 70 | 85 | 115 | 60 | 55 | 100 | 130 | 125 | ||
| У | 5,6 | 4,1 | 3,4 | 2,6 | 3,6 | 4,3 | 2,9 | 2,5 | 3,0 | 4,5 | ||||
| 31 | Х | 140 | 100 | 130 | 120 | 70 | 110 | 65 | 150 | 90 | 60 | 125 | ||
| У | 12,3 | 6,7 | 11,2 | 9,6 | 3,4 | 8,4 | 2,8 | 13,0 | 6,1 | 1,9 |
Выполнение и оформление работы (рассмотрим для варианта 31)
1. Построим диаграмму рассеивания по исходным данным для своего варианта
Y
10 5 50 100 150 X
Из диаграммы следует, что между показателями  и
и 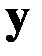 действительно наблюдается зависимость. Но сделать вывод -какая именно, трудно, поэтому рассмотрим все три регрессии, а затем выберем лучшую.
действительно наблюдается зависимость. Но сделать вывод -какая именно, трудно, поэтому рассмотрим все три регрессии, а затем выберем лучшую.
А) Рассмотрим линейную регрессию.
Составим исходную расчетную таблицу. Для удобства можно добавить в нее еще два столбца:  , чтобы сразу получить общую сумму квадратов.
, чтобы сразу получить общую сумму квадратов.
| № п/п | Объем товаро-оборота 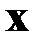 (тыс. руб.) (тыс. руб.)
| Издержки  (тыс. руб.) (тыс. руб.)
| 
| 
| 
| 
| 
| 
| 
|
| 1 | 140 | 12,6 | 19600 | 158,76 | 1764 | 12,2 | +0,4 | 0,16 | 3,17 |
| 2 | 100 | 6,7 | 10000 | 44,89 | 670 | 7,2 | -0,5 | 0,25 | 7,46 |
| 3 | 130 | 11,2 | 16900 | 125,44 | 1456 | 10,9 | +0,3 | 0,09 | 2,68 |
| 4 | 120 | 9,6 | 14400 | 92,16 | 1152 | 9,6 | 0 | 0 | 0 |
| 5 | 70 | 3,4 | 4900 | 11,56 | 238 | 3,3 | 0,1 | 0,01 | 2,94 |
| 6 | 110 | 8,4 | 12100 | 70,56 | 924 | 8,4 | 0 | 0 | 0 |
| 7 | 65 | 2,8 | 4225 | 7,84 | 182 | 2,7 | 0,1 | 0,01 | 3,57 |
| 8 | 150 | 13,0 | 22500 | 169 | 1950 | 13,4 | -0,4 | 0,16 | 3,08 |
| 9 | 90 | 6,1 | 8100 | 37,21 | 549 | 5,9 | 0,2 | 0,04 | 3,28 |
| 10 | 60 | 1,9 | 3600 | 3,61 | 114 | 2,1 | -0,2 | 0,04 | 10,53 |
| Итого | 1035 | 75,7 | 116325 | 721,03 | 8999 | 75,7 | 0 | 0,76 | 36,71 |
| Сред.зн. | 103,5 | 7,57 | 11632,5 | 72,1 | 899,9 | 7,57 | - | - | 3,671 |
Функция издержек выразится зависимостью:  .
.
 Для определения коэффициентов «a» и «b» воспользуемся методом наименьших квадратов (МНК):
Для определения коэффициентов «a» и «b» воспользуемся методом наименьших квадратов (МНК):
(1) 

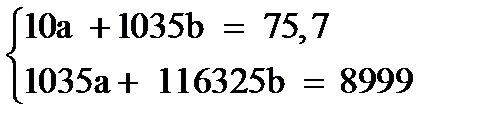
Домножим уравнение (1) системы на (-103,5), получим систему, которую решим методом алгебраического сложения.

9202,5b = 1164,05  или b = 0,12649.
или b = 0,12649.
Коэффициент регрессии b можно находить по формуле (2), не решая систему (1) непосредственно:
(2)  ,
, 
Результат аналогичен.
Теперь найдем коэффициент «a» из уравнения (1) системы (1):
10a = 75,7-1035b; 10a = 75,71035*0,12649; 10a =- 55,2;
a = -5,52.
Или можно «a» вычислить по формуле (3)  ,
,
 .
.
Уравнение регрессии будет иметь вид:  = -5,52 + 0,126 x
= -5,52 + 0,126 x
Затем, подставляя различные значения  из столбца 2, получим теоретические значения
из столбца 2, получим теоретические значения  для столбца 7:
для столбца 7:
 ,
,
аналогично для  …и
…и .
.
В столбце 8 находим разность текущего значения  и
и  (теоретического), найденного по формуле (4).
(теоретического), найденного по формуле (4).
Для расчета используем следующие формулы:
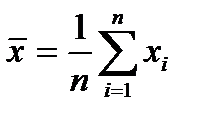 ,
,  ,
,  ,
,
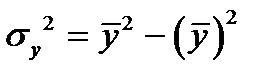 ,
,  ,
,  .
.
Коэффициент аппроксимации определим по формуле:
 .
.
Средняя ошибка аппроксимации:
 .
.
Допустимый предел значений  - не более 10 %, это говорит о том, что уравнение регрессии точно аппроксимирует исходную зависимость.
- не более 10 %, это говорит о том, что уравнение регрессии точно аппроксимирует исходную зависимость.
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции  . Найдем его по формуле для
. Найдем его по формуле для 
 .
.
Коэффициент  . Характер связи устанавливается по таблице Чеддока:
. Характер связи устанавливается по таблице Чеддока:
| Диапазон измерения | 0,1-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 |
| Характер тесноты связи | слабая | умеренная | заметная | высокая | весьма высокая |
В примере получилась связь прямая, весьма высокая.
Для вычисления коэффициента  , используются и другие формулы:
, используются и другие формулы:
 .
.
3. Дисперсионный анализ. Общая сумма квадратов отклонений (т.е. общая дисперсия ) равна:
 ,
,
где  - общая сумма квадратов отклонений,
- общая сумма квадратов отклонений,
 - сумма отклонений, обусловленная регрессией (факторная),
- сумма отклонений, обусловленная регрессией (факторная),
 - остаточная сумма квадратов отклонений.
- остаточная сумма квадратов отклонений.
 .
.
Остаточная сумма  определена в таблице в 9 столбце и равна 0,76. Тогда объясненная (факторная) сумма квадратов будет равна
определена в таблице в 9 столбце и равна 0,76. Тогда объясненная (факторная) сумма квадратов будет равна 
Долю дисперсии, объясняемую регрессией, в общей доле дисперсии  характеризует индекс детерминации
характеризует индекс детерминации 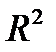 . Он определяется отношением объясненной дисперсии к общей
. Он определяется отношением объясненной дисперсии к общей  .
.
Качество всего уравнения регрессии в целом, проверяется F-тестом.
Составим таблицу дисперсионного анализа:
| Источники вариации | Число степеней свободы |
отклонений. | Дисперсия на 1 степ.свободы. | F отн | |
| Факт | табл. (0,05) | ||||
| общая | 9 | 147,98 | 
| 1549,68 | 5,32 |
| объясненная | 1 | 147,22 | 147,22 | ||
| остаточная | 8 | 0,76 | 0,095 | ||
Fтабл определяем по [1] в зависимости от уровня значимости (α = 0,05) и числа степеней свободы (df=8). Fтабл=5,32.
F-тест состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи rху.
Если Fфакт>Fтабл (1549>5,32), то гипотеза Но о случайной природе оцениваемых характеристик отклоняется и признается их значимость и надежность.
Б) Степенная регрессия 
Для того, чтобы построить степенную модель, необходимо линеаризовать переменные путем логарифмирования обеих частей уравнения  :
:

Пусть 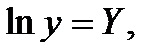

 , тогда
, тогда 
Рассчитываем  и b по формулам:
и b по формулам:


Все необходимые расчеты представлены в таблице 2.
| № п/п | x | y | X | Y | XY | X2 | Y2 | 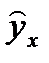
| 
| 
| Ai |
| 1 | 140 | 12,6 | 4,9416 | 2,5337 | 12,2053 | 24,4198 | 6,4196 | 11,6 | 1,0 | 1,0 | 7,9 |
| 2 | 100 | 6,7 | 4,6052 | 1,9021 | 8,7596 | 21,2076 | 3,6180 | 6,7 | 0 | 0 | 0 |
| 3 | 130 | 11,2 | 4,8675 | 2,4159 | 11,7594 | 23,6929 | 5,8366 | 10,7 | 0,5 | 0,25 | 3.73 |
| 4 | 120 | 9,6 | 4,7875 | 2,2617 | 10,8282 | 22,9201 | 5,1156 | 9,3 | 0,3 | 0,09 | 0,93 |
| 5 | 70 | 3,4 | 4,2485 | 1,2237 | 5,1702 | 18,0497 | 1,4976 | 3,7 | 0,3 | 0,09 | 2,64 |
| 6 | 110 | 8,4 | 4,7005 | 2,1282 | 10,0037 | 22,0945 | 4,5294 | 7,8 | 0,6 | 0,36 | 4,28 |
| 7 | 65 | 2,8 | 4,1744 | 1,0296 | 4,2980 | 17,4255 | 1,0601 | 3,4 | - 0,6 | 0,36 | 12,8 |
| 8 | 150 | 13,0 | 5,0106 | 2,5649 | 12,8519 | 25,1065 | 6,5790 | 12,9 | 0,1 | 0,01 | 0,08 |
| 9 | 90 | 6,1 | 4,4998 | 1,8083 | 8,1369 | 20,2483 | 3,2699 | 5,7 | 0,4 | 0,16 | 2,62 |
| 10 | 60 | 1,9 | 4,0943 | 0,6418 | 2,6279 | 16,7637 | 0,4120 | 2,9 | - 1,0 | 1,0 | 52,6 |
| Итого | 1035 | 75,7 | 45,9299 | 18,5099 | 86,6419 | 211,9286 | 37,9258 | 74,7 | 1,6 | 3,32 | 87,59 |
| Средн.зн. | 103,5 | 7,57 | 4,59299 | 1,85099 | 8,66419 | 21,19286 | 3,79258 | 8,759 |
Параметры будут равны: 
Подставим их в уравнение и получим линейное уравнение:

Потенцируя которое, получим:

По этому уравнению заполняется вторая половина таблицы.
В) Уравнение гиперболы 
Линеаризуется при замене 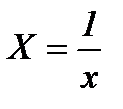 , тогда
, тогда 
Все необходимые расчеты представим в таблице 6.
| № п/п | x | y | 
| 
| 
| 
| 
| 
| Ai |
| 1 | 140 | 12,6 | 0,0071429 | 0,05 | 0,000051 | 10,7 | 1,9 | 3,61 | 15 |
| 2 | 100 | 6,7 | 0,01 | 0,067 | 0,0001 | 8,1 | -1,4 | 1,96 | 20 |
| 3 | 130 | 11,2 | 0,007692 | 0,086154 | 0,000059 | 10,3 | 0,9 | 0,81 | 8 |
| 4 | 120 | 9,6 | 0,008333 | 0,08 | 0,000069 | 9,6 | 0 | 0 | 0 |
| 5 | 70 | 3,4 | 0,014286 | 0,048571 | 0,000204 | 4,2 | -0,8 | 0,64 | 23 |
| 6 | 110 | 8,4 | 0,009091 | 0,076364 | 0,000083 | 8,9 | -0,5 | 0,25 | 5,9 |
| 7 | 65 | 2,8 | 0,015385 | 0,043077 | 0,000237 | 3,2 | -0,4 | 0,16 | 14 |
| 8 | 150 | 13,0 | 0,006667 | 0,086667 | 0,000044 | 11,3 | 1,7 | 2,89 | 13 |
| 9 | 90 | 6,1 | 0,011111 | 0,067778 | 0,000125 | 7,1 | -1 | 1 | 16 |
| 10 | 60 | 1,9 | 0,016667 | 0,031667 | 0,000278 | 2 | -0,1 | 0,01 | 5,2 |
| Сумма | 1035 | 75,7 | 0,106375 | 0,434124 | 0,001537 | 75,5 | 11,33 | 120,1 | |
| Ср. знач. | 103,5 | 7,57 | 0,0106375 | 0,0434124 | 0,000154 | 12 |
Найдем параметры  и
и 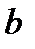 , используя МНК.
, используя МНК.
Для этого решим систему (1), учитывая, что  .
.
Таким образом, получили систему уравнений:
 :
:  :
:
Можно воспользоваться формулами.

Итак, получим уравнение:
 .
.
Оценим тесноту связи результативным фактором и факторным признаком с помощью индекса корреляции  (для нелинейных моделей) и коэффициента детерминации
(для нелинейных моделей) и коэффициента детерминации  , которые рассчитываются по следующим формулам:
, которые рассчитываются по следующим формулам:
 ,
,

Для степенной регрессии: 
Для гиперболы получим:……………………………………… 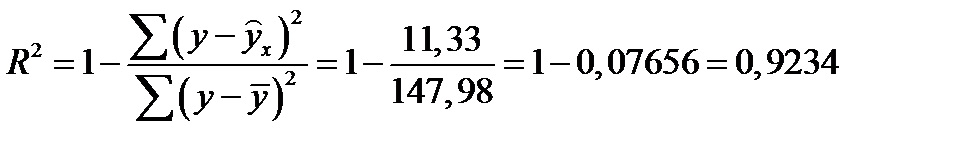
Найдем средний коэффициент эластичности по формулам, представленным в таблице 7.
Таблица 7
| Вид регрессии | Формула для расчета |
| Линейная | 
|
| Степенная | 
|
| Гиперболическая | 
|
Найдем среднюю ошибку аппроксимации по формуле:
 , где
, где  .
.
Оценим статистическую надежность результатов регрессионного моделирования с помощью F-критерия Фишера:
 .
.
Для степенной регрессии имеем:
 .
.
Для гиперболы
 .
.
Для линейном модели уже строили таблицу дисперсионного анализа
Для сравнения полученных уравнений регрессии построим следующую таблицу:
Таблица
| Вид регрессии |  , , 
| R2, r2 | 
| 
| F | 
|
| Линейная | 0,997 | 0,994 | 3,67 | 1,3973 | 1549 | 0,76 |
| Степенная | 0,988 | 0,978 | 8,76 | 1,2558 | 355,64 | 3,32 |
| Гиперболическая | 0,961 | 0,923 | 12 | 1,0796 | 95,90 | 11,33 |
Из итоговой таблицы видно, что коэффициент корреляции наибольший для линейной регрессии, коэффициент детерминации max, а коэффициент аппроксимации минимален, поэтому можно сделать вывод: наиболее сильное влияние на уровень издержек в зависимости от товарооборота получается при использовании в качестве аппроксимирующей функции линейную функцию.
Для всех моделей  , следовательно, все модели являются адекватными.
, следовательно, все модели являются адекватными.
Из таблицы видно, что лучшим уравнением регрессии является линейная функция, так как коэффициент детерминации для этой функции является наибольшим из представленных в таблице, сумма квадратов отклонений фактических значений результативного признака от расчетных является наименьшей и средний коэффициент аппроксимации является наименьшим.
Если получается, что коэффициент детерминации для нелинейной регрессии  больше
больше  коэффициента детерминации для линейной регрессии, надо рассмотреть модуль
коэффициента детерминации для линейной регрессии, надо рассмотреть модуль  . Если разность небольшая, т.е. условие модуля выполняется, то все равно выбираем линейную регрессию для дальнейших расчетов.
. Если разность небольшая, т.е. условие модуля выполняется, то все равно выбираем линейную регрессию для дальнейших расчетов.
Чем больше кривизна линии регрессии, тем 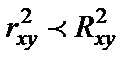 <
< 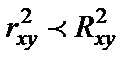 . Если
. Если  превышает 0,1, то предположение о линейной форме связи считается не оправданным. В этом случае проводится оценка существенности различия
превышает 0,1, то предположение о линейной форме связи считается не оправданным. В этом случае проводится оценка существенности различия  по критерию Стьюдента.
по критерию Стьюдента. 

 - ошибка разности между
- ошибка разности между  и
и 

Если t<2, то различия между  и
и  несущественны, и возможно применение линейной регрессии.
несущественны, и возможно применение линейной регрессии.
Если t>2, то различия существенны и замена нелинейной регрессии уравнением линейной функции невозможна.
В нашем примере лучшей является линейная модель. Для линейнойрегрессии выполним дальнейшие расчеты.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитывают t-критерий.
Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
 ,
,  ,
,  .
.
 , т.к.
, т.к. 
где  , или из табл. дисперсионного анализа (0,095).
, или из табл. дисперсионного анализа (0,095).
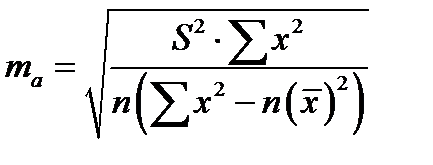 ,
,  .
.
Для примера определим стандартную ошибку для параметра «b»:
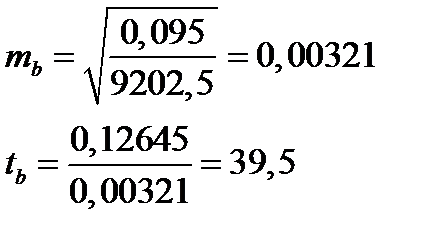
Критерий Стьюдента для параметра «b» равен 39,5.
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством:

 , 39,52=1560.
, 39,52=1560.
Табличное значение tтабл критерия Стьюдента определяем по [1] для и уровня значимости 0,05 и числа степеней свободы df = 8,  , т.к.
, т.к.  >
>  , то гипотезу о несущественности коэффициента регрессии можно отклонить.
, то гипотезу о несущественности коэффициента регрессии можно отклонить.
Для расчета доверительного интервала определяем предельную ошибку  для каждого показателя:
для каждого показателя:


Доверительный интервал,  ,
,  .
.
Для расчета доверительного интервала для параметра а, найдем:

 , т.к. критерий Стьюдента двусторонний, а параметр а - отрицательный, то он значим. Найдем для него доверительный интервал:
, т.к. критерий Стьюдента двусторонний, а параметр а - отрицательный, то он значим. Найдем для него доверительный интервал:

Найдем доверительный интервал для параметра r:

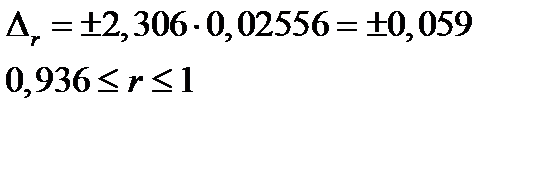
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательная, а верхняя положительная, то оцениваемый параметр принимается нулевым, т.к. не может одновременно принимать и положительное и отрицательное значения.
Прогнозное значение  определяется путем подстановки в уравнение регрессии:
определяется путем подстановки в уравнение регрессии:

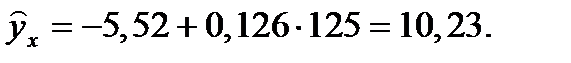
Вычислим ошибку прогноза для уравнения  :
:
 .
.
И для уравнения  :
:
(*)  ,
,
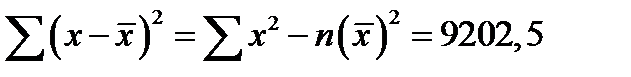 ,
,
 .
.
Для *  ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Для уравнения с  :
:
 ,
,
 .
.
9. При оценке параметров уравнения регрессии мы использовали МНК. При этом делаются определенные предпосылки относительно случайной составляющей ei. Исследование остатков  предполагает наличие следующих пяти предпосылок МНК:
предполагает наличие следующих пяти предпосылок МНК:
1. Случайный характер остатков.
Чтобы проверить случайный характер остатков строится график зависимости ei от  . Из первой таблицы своего варианта берем два столбца
. Из первой таблицы своего варианта берем два столбца  и
и  . Приведены данные не для варианта 31, а другого
. Приведены данные не для варианта 31, а другого
| № | ŷх | 
|
| 1 | 3,995 | 0,2049 |
| 2 | 10,986 | -0,186 |
| 3 | 8,364 | 1,2356 |
| 4 | 6,617 | -0,317 |
| 5 | 7,490 | -0,091 |
| 6 | 5,742 | 0,4572 |
| 7 | 12,734 | -1,334 |
| 8 | 4,869 | -1,569 |
| 9 | 11,860 | 0,3401 |
| 10 | 9,238 | 1,2617 |
По этим данным строится график зависимости eiот  .Если на графике получена горизонтальная полоса, то это означает что остатки не зависят от полученных теоретических значений
.Если на графике получена горизонтальная полоса, то это означает что остатки не зависят от полученных теоретических значений  . Можно сделать вывод о случайном характере остатков (зависимость отсутствует), т.е.
. Можно сделать вывод о случайном характере остатков (зависимость отсутствует), т.е.  хорошо аппроксимирует фактические значения. Если не получается полоса, а появляется зависимость eiот
хорошо аппроксимирует фактические значения. Если не получается полоса, а появляется зависимость eiот  , то МНК использовать нельзя, нужно построить новое уравнение регрессии или добавить другие переменные в уравнение регрессии.
, то МНК использовать нельзя, нужно построить новое уравнение регрессии или добавить другие переменные в уравнение регрессии.

У нас на графике получена горизонтальная полоса и остатки представляют собой случайные величины и МНК оправдан.
2. Нулевая средняя величина остатков, не зависящая от хj
Нужно проверить математическое ожидание остатков равно 0.  . Зависимость отсутствует.
. Зависимость отсутствует.
| № | х | 
|
| 1 | 50 | 0,2049 |
| 2 | 130 | -0,186 |
| 3 | 100 | 1,2356 |
| 4 | 80 | -0,317 |
| 5 | 90 | -0,091 |
| 6 | 70 | 0,4572 |
| 7 | 150 | -1,334 |
| 8 | 60 | -1,569 |
| 9 | 140 | 0,3401 |
| 10 | 110 | 1,2617 |
| Итого | 980 | 0 |
По этим данным строится график зависимости ei от  .Если на графике расположения остатков не имеет направленности, то это означает то остатки не зависят от значений
.Если на графике расположения остатков не имеет направленности, то это означает то остатки не зависят от значений  . Если же график показывает наличие зависимости ei от
. Если же график показывает наличие зависимости ei от  , то модель не адекватна. Причины неадекватности могут быть разные. В этом случае проводят корректировку модели, в частности использовать кусочно-линейные модели.
, то модель не адекватна. Причины неадекватности могут быть разные. В этом случае проводят корректировку модели, в частности использовать кусочно-линейные модели.

Из графика следует, что нет зависимости между  и
и  j, т.е. модель адекватна. Остатки независимы от значений х.
j, т.е. модель адекватна. Остатки независимы от значений х.
3.Проверка на гомоскедастичность.
ИИспользуем метод ранговой корреляции Спирмэна. Проранжируем факторы Х и абсолютные величины 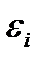 по возрастанию фактора.
по возрастанию фактора.
|
№ п/п | Х |
| Расчет ранговой корреляции | ||||
| Rx | R| 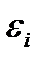 | |
| d= Rx- R| 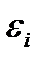 | |
| d2 | ||||
| 1 | 50 | 0,2049 | 1 | 3 | -2 | 4 | |
| 2 | 60 | -1,569 | 2 | 10 | -8 | 64 | |
| 3 | 70 | 0,457 | 3 | 6 | -3 | 9 | |
| 4 | 80 | -0,317 | 4 | 4 | 0 | 0 | |
| 5 | 90 | -0,091 | 5 | 1 | 4 | 16 | |
| 6 | 100 | 1,236 | 6 | 7 | -1 | 1 | |
| 7 | 110 | 1,262 | 7 | 8 | -1 | 1 | |
| 8 | 130 | -0,186 | 8 | 2 | 6 | 36 | |
| 9 | 140 | 0,340 | 9 | 5 | 4 | 16 | |
| 10 | 150 | -1,334 | 10 | 9 | 1 | 1 | |
| Итого |
|
|
|
|
| 148 | |
Коэффициент ранговой корреляции Спирмена


Сравниваем это значение с табличным при 5%-м уровне значимости и числе степеней свободы df = 8  т.к. 0,2929 < 2,306, то на уровне значимости 5% принимается гипотеза об отсутствии гетероскедастичности.
т.к. 0,2929 < 2,306, то на уровне значимости 5% принимается гипотеза об отсутствии гетероскедастичности.
4. Отсутствие автокорреляции остатков.
Это значит, что остатки  i распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений.
i распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений.  i – текущие,
i – текущие,  j – предыдущие. Пусть j=i-1, n=10, отбрасываем одно значение будетn-1=9
j – предыдущие. Пусть j=i-1, n=10, отбрасываем одно значение будетn-1=9
| № п/п |  j j
|  i i
|  i* i*  j j
|  j2 j2
|  i2 i2
|
| 1 | 0,2049 | ||||
| 2 | -0,186 | 0,2049 | -0,03811 | 0,0346 | 0,04198 |
| 3 | 1,236 | -0,186 | -0,2299 | 1,5277 | 0,0346 |
| 4 | -0,317 | 1,236 | -0,3918 | 0,1005 | 1,5277 |
| 5 | -0,091 | -0,317 | 0,0288 | 0,0083 | 0,1005 |
| 6 | 0,4572 | -0,091 | -0,0416 | 0,2090 | 0,0083 |
| 7 | -1,334 | 0,4572 | -0,6099 | 1,7796 | 0,2090 |
| 8 | -1,569 | -1,334 | 2,0930 | 2,4618 | 1,7796 |
| 9 | 0,340 | -1,569 | -0,5335 | 0,1156 | 2,4618 |
| 10 | 1,262 | 0,340 | 0,4291 | 1,5926 | 0,1156 |
| 1.262 | |||||

| -0,2018 | -1,262 | 0,70609 | 7,8297 | 6,2710 |
| ср. зн. | -0,0224 | -0,1402 | 0,0785 | 0,87 | 0,6968 |

 0,0785 – (-0,0224)(-0,1402) = 0,07536
0,0785 – (-0,0224)(-0,1402) = 0,07536



 при 9 – 2 = 7 степенях свободы явно незначимо и демонстрирует отсутствие автокорреляции остатков.
при 9 – 2 = 7 степенях свободы явно незначимо и демонстрирует отсутствие автокорреляции остатков.
5. Остатки подчиняются нормальному закону распределения.
Эта предпосылка позволяет проводить проверку параметров регрессии и корреляции с помощью t- и F-критериев. Даже если предпосылка не выполняется, МНК дает хорошие результаты.
Вывод: все предпосылки проверены, метод наименьших квадратов использован верно для расчета коэффициентов уравнения регрессии.
Дата добавления: 2018-05-12; просмотров: 289; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 квадр.
квадр.