ТЕМА 7 Дифференциальное исчисление функций нескольких переменных
Министерство сельского хозяйства Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
Казанский государственный аграрный университет
Кафедра физики и математики
МАТЕМАТИКА
Семестр 2
Учебно-методическое пособие
Для студентов заочной формы обучения
Казань 2018
ТЕМА 6 Интегральное исчисление функции
Одной Переменной
Неопределенный интеграл. Основные понятия и свойства
Неопределенным интегралом от функции  называется выражение вида
называется выражение вида  если
если  . Функция
. Функция  называется первообразной для заданной функции
называется первообразной для заданной функции  .
.
Свойства неопределенного интеграла:
1. 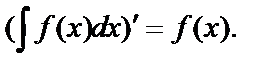
2. 
3. 
4.  , где A ≠ 0.
, где A ≠ 0.
5. 
6.2 Таблица основных неопределенных интегралов
1.  где
где  (
(  ).
).
2. 
3. 
4. 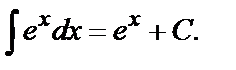
5. 
6. 
7. 
8. 
9. 
10. 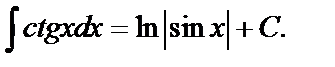
11. 
12. 
13. 
14. 
15. 
16. 
Основные методы интегрирования
Интегрирование способом подстановки
В основе интегрирования способом подстановки (или замены переменной) лежит свойство инвариантности формул интегрирования, которое заключается в следующем: если  , то
, то  , где
, где  - произвольная дифференцируемая функция от x.
- произвольная дифференцируемая функция от x.
Замена переменной в неопределенном интеграле производится с помощью подстановки:  , где t – новая переменная, а
, где t – новая переменная, а 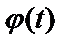 – непрерывно дифференцируемая функция. В этом случае формула замены переменной:
– непрерывно дифференцируемая функция. В этом случае формула замены переменной:
 (6.1)
(6.1)
|
|
|
Функцию 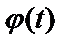 стараются выбирать таким образом, чтобы правая часть формулы приобрела более удобный для интегрирования вид.
стараются выбирать таким образом, чтобы правая часть формулы приобрела более удобный для интегрирования вид.
Интегрирование по частям
Интегрирование по частям называется нахождение интеграла по формуле:
 (6.2)
(6.2)
где u и v – непрерывно дифференцируемые функции от x. С помощью формулы (6.2) отыскание интеграла  сводится к нахождению другого интеграла
сводится к нахождению другого интеграла  ; ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
; ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
При этом в качестве u берется функция, которая при дифференцировании упрощается, а в качестве v – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Так, при нахождении интегралов вида

за u следует принять многочлен P(x), а за dv - соответственно выражения  при отыскании интегралов вида
при отыскании интегралов вида 
 за u принимаются соответственно функции
за u принимаются соответственно функции  , а за dv – выражение
, а за dv – выражение  .
.
Интегрирование рациональных дробей
Интегрирование рациональных дробей, т.е. отношений двух многочленов  и
и  (соответственно
(соответственно  й и n
й и n  й степени):
й степени):  сводится к разложению подынтегральной функции
сводится к разложению подынтегральной функции 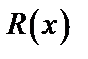 на элементарные, всегда интегрируемые дроби вида:
на элементарные, всегда интегрируемые дроби вида:
 , (6.3)
, (6.3)
|
|
|
где l и m –целые положительные числа, а трехчлен  не имеет действительных корней. При этом в случае неправильной дроби (
не имеет действительных корней. При этом в случае неправильной дроби (  ) должна быть предварительно выделена целая часть.
) должна быть предварительно выделена целая часть.
Определенный интеграл. Формула Ньютона-Лейбница.
Формула Ньютона-Лейбница для вычисления определенного интеграла имеет вид:
 (6.4)
(6.4)
если  и первообразная
и первообразная  непрерывна на отрезке
непрерывна на отрезке  .
.
Определенный интеграл численно равен площади криволинейной трапеции, ограниченной прямыми x=a, x=b, y=0 и частью графика функции  взятой со знаком плюс, если
взятой со знаком плюс, если  , и со знаком минус, если
, и со знаком минус, если  .
.
Решение типового задания
Пример 1. Найти  .
.
Решение.Применим метод подстановки. Положим  , тогда
, тогда  . Используя формулу (6.1), имеем
. Используя формулу (6.1), имеем
 .
.
Пример 2. Найти  .
.
Решение. Применим метод интегрирования по частям. Положим  ,
,  тогда
тогда 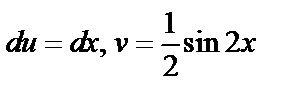 . Используя формулу (6.2), имеем
. Используя формулу (6.2), имеем
 .
.
Пример 3. Найти  .
.
Решение. Подынтегральная рациональная дробь является правильной и разлагается на элементарные дроби вида (6.3):
 .
.
Освобождаясь от знаменателей в обеих частях этого равенства и приравнивая числители, получаем тождество для вычисления неопределенных коэффициентов  :
:
 .
.
Составим систему трех уравнений с тремя неизвестными. Одно уравнение получим, полагая х=2 (корень знаменателя подынтегральной функции). Два других получим, приравнивая коэффициенты при одинаковых степенях х в обеих частях тождества, например  и
и  при:
при:
|
|
|

Решение этой системы дает:  . Таким образом,
. Таким образом,


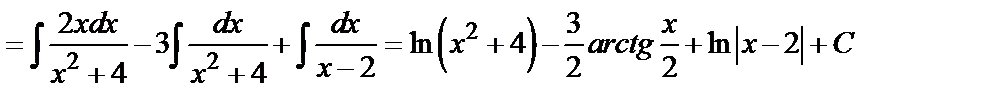 .
.
Задачи 181-210:
Вычислите неопределенные интегралы:
181. а) 
| б) 
| в) 
|
182. а) 
| б) 
| в) 
|
183. а) 
| б) 
| в) 
|
184. а) 
| б) 
| в) 
|
185. а) 
| б) 
| в) 
|
186. а) 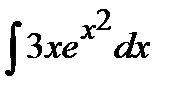
| б) 
| в) 
|
187. а) 
| б) 
| в) 
|
188. а) 
| б) 
| в) 
|
189. а) 
| б) 
| в) 
|
190. а) 
| б) 
| в) 
|
191. а) 
| б) 
| в) 
|
192. а) 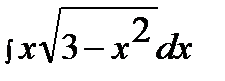
| б) 
| в) 
|
193. а) 
| б) 
| в) 
|
194. а) 
| б) 
| в) 
|
195. а) 
| б) 
| в) 
|
196. а) 
| б) 
| в) 
|
197. а) 
| б) 
| в) 
|
198. а) 
| б) 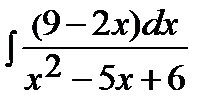
| в) 
|
199. а) 
| б) 
| в) 
|
200. а) 
| б) 
| в) 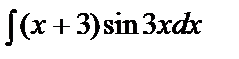
|
201.a) 
| б) 
| в) 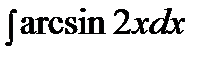
|
202. a) 
| б) 
| в) 
|
203. a) 
| б) 
| в) 
|
204. a) 
| б) 
| в) 
|
205. a) 
| б) 
| в) 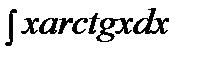
|
206. a) 
| б) 
| в) 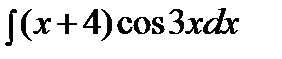
|
207. a) 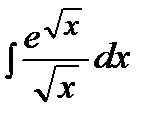
| б) 
| в) 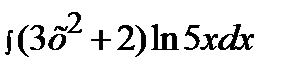
|
208. a) 
| б) 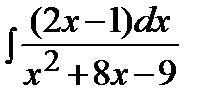
| в) 
|
209. a) 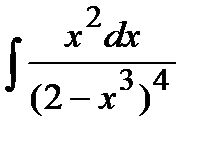
| б) 
| в) 
|
210.a) 
| б) 
| в) 
|
Задачи 211-240:
Вычислить площадь фигуры, ограниченной данными линиями: Сделать чертеж и заштриховать искомую площадь.
211.  
| 226.  
|
212.  
| 227.  
|
213.  
| 228.  
|
214.  
| 229.  
|
215.  
| 230.  
|
216.  
| 231.  
|
217.  
| 232.  
|
218.  
| 233.  
|
219.  
| 234.  
|
220. 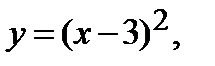 
| 235. 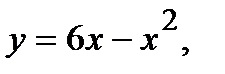 
|
211.  
| 236.  
|
222.  
| 237. 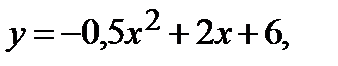 
|
223.  
| 238.  
|
224.  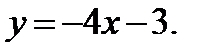
| 239.  
|
225.  
| 240.  
|
ТЕМА 7 Дифференциальное исчисление функций нескольких переменных
|
|
|
Дата добавления: 2018-05-12; просмотров: 252; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
