Особенности расчета цепей, содержащих зависимые источники.
Методы расчета сложных электрических цепей Недостатком метода расчета, основанным на непосредственном применении законов Кирхгофа компонентных уравнений, является то, что число уравнений равно числу неизвестных токов ветвей. Для сложных цепей, содержащих большое число ветвей, данный метод становится чрезмерно громоздким. Уменьшить число уравнений позволяют косвенные методы, в которых используется один закон Кирхгофа (первый или второй).К таким методам относится : 1) метод контурных токов; 2) метод узловых напряжений (потенциалов).
Метод контурных токов
Для применения метода контурных токов MKT предварительно необходимо преобразовать электрическую цепь в схему замещения, содержащую только комплексные источники напряжения и комплексные сопротивления. MKT заключается в том, что вместо токов ветвей на основании второго закона Кирхгофа определяется так называемые контурные токи, замыкающиеся в контурах.
Для примера рассмотрим двухконтурную цепь (Рисунок 2.29), в котором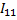 
и 
-контурные токи.
Рисунок 2.29 Двухконтурная электрическая схема
Токи ветвей 
, 
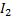и 
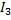в соответствии с первым законом Кирхгофа определяется через контурные токи: 
; 
; 
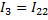. Отметим, что направление контурных токов задается произвольно. Направление обхода контура обычно берется совпадающим с направлением контурного тока.
Для схемы рисунок 2.29 по второму закону Кирхгофа можно записать два уравнения через контурные токи:
|
|
|
(2.83) 
Система уравнений (2.83) может быть представлена (2.83) в матричной форме:
(2.84) 
решение системы (,2.84)относительно неизвестных токов 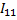и :
(2.85) 
и 
,
Где 
и - алгебраические дополнения, а 
– определитель матрицы [Z].
Алгебраические дополнения и 
являются определителями матрицы [Z] , в которой первый и второй столбцы заменяются столбцам напряжений соответственно:
(2.86) 
; 
.
Представленный выше порядок составления контурных уравнений можно распространить на произвольную линейную цепь. Для этого введем ряд обозначений:
1. 
- собственное сопротивление контура, которое равно сумме всех сопротивлений i-oro контура
2. 
- общее или взаимное сопротивление, равное сумме сопротивлений ветвей,
являющимся общими для i-го к-oго контуров
3. 
-контурная ЭДС , равная алгебраической сумме источников напряжения
входящих в I -й контур.
Для схемы (Рисунок 2.29): собственные сопротивления: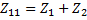 
; 
; общие сопротивления: 
; 
; контурные: 
; 
.
С учетом введенных обозначений предлагается следующий алгоритм составления контурных уравнений для произвольной линейной цепи :
|
|
|
1. Пассивные элементы цепей (R, L, С) заменяются их комплексными сопротивлениями 
, 
, 
.
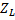2. Имеющиеся в цепи источники тока, путем эквивалентного преобразования, заменяются на комплексные источники ЭДС.
3. Определяется число независимых контуров, для которых составляются контурные управления. Число независимых контуров 
, где р - число ветвей, q - комплект узлов.
4. Назначаются контурные токи, при этом направление обхода контуров совпадает с напряжением контурных токов.
5. Составляется матрица контурных сопротивлений, в которой по главной диагонали находится собственные сопротивления контуров ( 
, 
… ).
Остальные члены матрицы [Z] являются общимисопротивлениями 
( 
и т.д.)
При этом, если контурные токи направлены навстречу друг другу ( 
), то берется со знаком минус, и если совпадают по на правлению ( 
), то плюс. При отсутствии общих ветвей между контурами, или отсутствия сопротивления в общей ветви 
.
6. Составляется матрица столбец контурных ЭДС ( 
), при этом, напряжениеисточника берется со знаком плюс, если его направление совпадает с напряжением контурного тока.
7. Система линейных уравнений разрешается любым известным методом (Крамера, редукции Гаусса) относительно контурных токов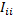 
.
|
|
|
8. Определяются токи ветвей через контурные токи с учетом их условно-положительного направления.
При этом, система уравнений в матричной форме будет выглядеть в виде:
(2.86) 
,
Где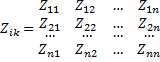 
- матрица контурных сопротивлений;
- столбец контурных токов;
- столбец контурных напряжений ;n -число контуров
Приведем пример составления уравнений в матричной форме по MKT для схемы, изображенной на (Рисунке 2.30)
Пример 
=
Рис. 2.30 Электрическая схема (а) и ее схема замещения по МКТ(б).
Представленная на (Рисунке 2.30 (а)) электрическая схема содержит 6 ветвей и 4 узла, поэтому число независимых контуров равно: 
. Преобразуем исходную схему в соответствующую MKT схему замещения.
Обозначим независимые контура и задания направлением контурных токов (Рисунок 2.30 (б)). Определим контурные сопротивления: 
; 
; 
– собственные сопротивления контуров; 
; 
; 
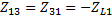- общие (взаимные) сопротивления. Все общие сопротивления берутся со знаком минус, т.к. контурные токи в них направлены навстречу друг другу. Следующим шагом найдем контурные ЭДС: 
; 
; 
. Система контурных уравнений в матричной форме будет выглядеть в следующем виде:
(2.87) 
токи ветвей определяются через контурные токи: ; 
; 
; 
; 
; 
.
|
|
|
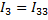Метод узловых напряжений
В основе метода узловых напряжений используется первый закон Кирхгофа, в соответствии с которым число независимых уравнений равно: 
. Один из узлов схемы принимается базовым (опорным). Напряжения в остальных узлах относительно базового называются узловыми напряжениями.
Так в любой ветви находится как произведение проводимости ветви на разность узловых напряжений на концах данной ветви. Таким образом, зная узловые напряжения в электрической цепи, можно найти токи в ветвях.
Если принять потенциал базового узла равным нулю, то напряжение между остальными узлами и базовым будут равны потенциалам этих узлов. Поэтому данный метод также называется методом узловых потенциалов (МУП).
Предварительно в расчетной схеме по МУП все комплексные сопротивления заменяются на комплексные проводимости ( 
), а имеющиеся источники напряжения преобразуются в источники тока. Рассмотрим в качестве примера МУП схему, изображенную на Рис. 2. 31
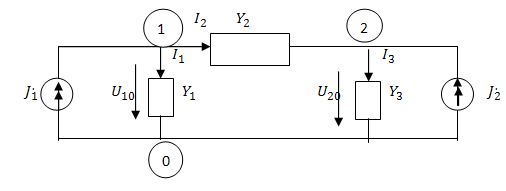
Рис. 2.31 Пример к методу узловых напряжений.
Схема Рис. 2.31 содержит три узла (0,1,2), в которой за базовый выберем нулевой узел. Узловые напряжения в первой и втором узлах обозначим через 
и 
.
В соответствии с первым законом Кирхгофа для узла 1 и узла 2 запишем:
(2.88)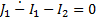 
Выразим токи ветвей через узловые напряжения ( 
) и подставим в уравнение (2.88)
(2.89) 
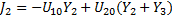
Перепишем уравнение (2.89) в виде матрицы:
(2.90) [ 
]= 
Обозначим через 
- собственная проводимость 1-ого узла,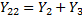 
- второго узла, которые равны сумме проводимости сходящихся в узлах ветвей.
Величина 
, входящая в уравнение (2.89) со знаком минус называется взаимной проводимостью между 1-ым и 2-ым узлом 
и между 2-ым и 1-ым узлами 
.
В общем случае для схемы, содержащей q-узлов, получается система из q-1 уравнений следующего вида:
(2.91) 
Где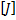 
- матрица столбец узлового тока, которая равняется сумме источников тока, подключаемых к узлу. При этом подходящий к узлу источник тока берется со знаком плюс, а отходящий – со знаком минус. 
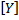- матрица проводимостей, в которой по диагонали расположены собственное значение проводимости - 
, взаимные проводимости между узлами берутся со знаком минус.
Отметим, что для схем, не содержащих зависимых источников, матрица 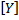симметрична относительно главной диагонали, т.е. 
и т.д.
Неизвестными в данной системе уравнений являются узловые напряжения 
, которые находятся любым известным методом решения линейных уравнений.
Например, используя формулу Крамера, можно записать, что:
, где 
– алгебраическое дополнение элемента 
определителя системы;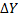 
- определитель матрицы .
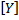Для приведенного выше примера имеем:
.
В общем случае порядок составления узловых уравнений по МУП
1. Электрическая схема преобразуется в комплексную схему замещения, в которой элементы или их соединения представляются комплексными проводимостями;
2. Имеющиеся источники напряжения преобразовываются в комплексные источники тока;
3. Один из узлов схемы берется за базовый, которому присваивается номер «0», остальные нумеруются;
4. Составляется матрица проводимостей [Y], состоящая из собственных и взаимных проводимостей, а также матрица столбец узловых токов;
5. Записывается система уравнений в матричном виде (2.91), которая разрешается относительно узловых напряжений.
Пример
Составить по МУП систему узловых напряжений для схемы, изображенной на Рис. 2.32
а) б)
Рис. 2.32 Электрическая схема (а) и ее схема замещения(б) по МУП.
На схеме замещения 2.32 (б) 
.
Схема имеет три узла, один из которых базовый, поэтому система узловых уравнений равна двум:
(2.92) 
Особенности расчета цепей, содержащих зависимые источники.
Метод узловых напряжений применяется и для цепей, содержащих зависимые источники. Схемы с зависимыми источниками, как правило, используются для моделирования биполярных и полевых транзисторов, в которых в основном применяются зависимые источники тока, управляемые током или напряжением. Порядок составления узловых уравнений для схем с зависимыми источниками тока следующий:
1. Вначале полагаем, что все источники тока независимы и составляем систему узловых уравнений в матричном виде (2.91).
2. Зависимые источники тока записываются в матрицу-столбец узловых токов через узловые напряжения уравнения ( 
, 
- управляющее напряжение)
3. Коэффициент пропорциональности S переносится в соответствии с правилом переноса в матрицу, в которой номер строки соответствует номеру узла подключения зависимого источника, а номера столбцов соответствуют номерам узлов управляющего напряжения.
Пример.
Рассмотрим в качестве примера схему с зависимым источником, изображенную на Рис. 2.33
Рис. 2.33 Схема с зависимым источником (а), и ее схема замещения (б).
Вначале в соответствии с МУП для схемы рис 2.33 (б) записываем систему узловых напряжений в виде:
(2.94) 
Переносим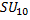 
из правой части в левую и записываем систему уравнений:
(2.95) 
Дата добавления: 2018-05-12; просмотров: 1122; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!