Первая теорема Больцано-Коши.
Билет №1.
Доказать теорему Ролля.
Пусть дана функция  .
.
1. Определена и непрерывна на отрезке  .
.
2. Дифференцируема на интервале  .
.
3. И на концах отрезка принимает одинаковые значения.  .
.
Тогда найдется, по крайней мере, 1 
 , принадлежащая интервалу
, принадлежащая интервалу  .
.
Доказательство: Т.к. функция  непрерывна на отрезке
непрерывна на отрезке  , то согласно 2 теореме Вейерштрасса она достигает своего минимального и максимального значения.
, то согласно 2 теореме Вейерштрасса она достигает своего минимального и максимального значения.
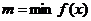 ,
,  ,
,
 ,
,  .
.
Случаи:
1.  ,
,  - любое из интервала
- любое из интервала 
2.  в силу 3-го условия теоремы, одно из значений минимального или максимального достигается функцией во внутренней точке интервала
в силу 3-го условия теоремы, одно из значений минимального или максимального достигается функцией во внутренней точке интервала  .
.
Согласно второму условию теоремы Ролля, функция дифференцируема на интервале  в любой точке, то по теореме Ферма существует
в любой точке, то по теореме Ферма существует  .
.
Доказать теорему о предельном переходе в неравенстве.
Пусть 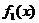 при
при  имеет конечный предел А1,
имеет конечный предел А1,  при
при  имеет конечный предел А2, и существует
имеет конечный предел А2, и существует  :
:  для
для  , тогда
, тогда  .
.
Доказательство:
 ,
, 
 ,
, 



Пусть 
Это неравенство выполняется для любого  ,
,  отсюда
отсюда 
Билет №2.
Доказать теорему Лагранжа.
Пусть функция  .
.
4. Определена и непрерывна на отрезке  .
.
5. Дифференцируема на интервале  .
.
Тогда существует  из интервала
из интервала  .
.
Доказательство: Рассмотрим вспомогательную функцию  , где
, где  - константа.
- константа.

1. Она непрерывна на 
2. дифференцируема на  .
.
Все условия теоремы Ролля выполняются  существует
существует  из
из 

Формула Маклорена для 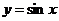 с остаточным членом в форме Пеано.
с остаточным членом в форме Пеано.
 , где
, где
|
|
|
1)  Пеано
Пеано
2)  где
где  - Лагранж
- Лагранж
3)  - Коши
- Коши
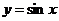 ,
,  ,
,  ,
, 
 , т.к. sin x - нечет., то вып. усл.:
, т.к. sin x - нечет., то вып. усл.: 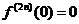
Билет №3.
Формула Маклорена для  с остаточным членом в форме Пеано.
с остаточным членом в форме Пеано.
 , где
, где
1)  Пеано
Пеано
2)  где
где  - Лагранж
- Лагранж
3)  - Коши
- Коши
 ,
,  ,
,  ;
; 
Сравнение на бесконечности роста показательной, степенной и логарифмических функций.
1) 
 , где s>0, x>0;
, где s>0, x>0;  .
. 
2)  ;
;  ;
;  =
=  ;
; 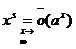 .
.
3)  (по транзитивности)
(по транзитивности) 
Билет №4.
Доказать первое достаточное условие экстремума функции.
Пусть функция  определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
Доказательство: Рассмотрим точку X из указанной окрестности, тогда:
1. на 
 - непрерывна.
- непрерывна.
2. на  - дифференцируема.
- дифференцируема.
По т. Лагранжа  , где
, где  , т.к.
, т.к. 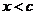 , то
, то 
на 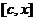 :
:  где
где  ,
, 
Доказать теорему о связи функции, её предела и бесконечно малой.
Для того, чтобы функция  , определённая в
, определённая в  имела конечный предел при
имела конечный предел при  , необходимо и достаточно чтобы эту функцию можно было представить в виде суммы предела и б.м.ф. при
, необходимо и достаточно чтобы эту функцию можно было представить в виде суммы предела и б.м.ф. при  (
( 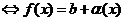 , где
, где  - б.м.ф. при
- б.м.ф. при  ).
).
Доказательство: I Необходимость:
|
|
|
Дано: 
Доказать: 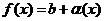 , где
, где  - б.м.ф. при
- б.м.ф. при  .
.

Пусть  по определению б.м.ф
по определению б.м.ф  - б.м.ф. при
- б.м.ф. при  .
.

II Достаточность:
Дано: 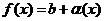 , где
, где  - б.м.ф. при
- б.м.ф. при  .
.
Доказать: 

Билет №5.
Доказать второе достаточное условие экстремума.
Пусть функция  определена и имеет в окрестности точки с производную до n-го порядка включительно, причем в самой точке с все производные до (n-1)-го порядка включительно равны 0, а n-ая производная в точке С отлична от нуля. Если n – четное, тогда С – точка локального экстремума, в частности, если
определена и имеет в окрестности точки с производную до n-го порядка включительно, причем в самой точке с все производные до (n-1)-го порядка включительно равны 0, а n-ая производная в точке С отлична от нуля. Если n – четное, тогда С – точка локального экстремума, в частности, если  , то x=c – локальный минимум, если
, то x=c – локальный минимум, если 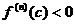 , то x=c – локальный максимум.
, то x=c – локальный максимум.
Доказательство: Запишем формулу Тейлора с остаточным членом в форме Пеано с центром в точке С.
 , где
, где  - б.м.ф. при
- б.м.ф. при  . Пусть n – четное, тогда
. Пусть n – четное, тогда  не меняет знак при переходе через С.
не меняет знак при переходе через С. 
 в которой функция сохраняет знак своего предела.
в которой функция сохраняет знак своего предела.  ,
,  .
.  .
.  , если
, если 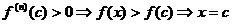 - точка локального экстремума.
- точка локального экстремума.
Вывести уравнение наклонной асимптоты.
Прямая  - называется правосторонней наклонной асимптотой графика
- называется правосторонней наклонной асимптотой графика  при
при  , если
, если  , где
, где  -б.м.ф. при
-б.м.ф. при  . Прямая
. Прямая  - называется левосторонней наклонной асимптотой графика
- называется левосторонней наклонной асимптотой графика  при
при  , если
, если  , где
, где  -б.м.ф. при
-б.м.ф. при  . Если
. Если  ,
,  , то y=kx+b – двусторонняя наклонная асимптота.
, то y=kx+b – двусторонняя наклонная асимптота.
Теорема. Для того, чтобы y=kx+b была правосторонней (левосторонней) наклонной асимптотой y=  при
при  (при
(при  ) необходимо существование двух пределов:
) необходимо существование двух пределов:  ;
;  И достаточно существование
И достаточно существование  .
.
|
|
|
Необходимость Дано: y=kx+b – правосторонняя наклонная асимптота.
Доказать:  ;
;  .
.
Док-во:  , где
, где  - б.м.ф. ;
- б.м.ф. ;  .
.  . Т.к.
. Т.к.  И
И 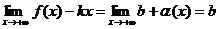 .
.
Достаточность Дано: 
Доказать: y=kx+b – правосторонняя наклонная асимптота.
Док-во. Т.к. существует предел  , то
, то  .
.  - правосторонняя наклонная асимптота (из определения).
- правосторонняя наклонная асимптота (из определения).
Билет №6.
Доказать необходимое условие возрастания дифференцируемой функции.
Для того, чтобы  , определённая и дифференцируемая на интервале (а;b) была возраст. на этом интервале, необходимо, чтобы ,
, определённая и дифференцируемая на интервале (а;b) была возраст. на этом интервале, необходимо, чтобы ,  .
.
Дано:f(x)-возраст.
Док-ть:  .
.
Доказательство: из опред. возраст. ф-ции 
 ;
;
 ;
;
 если
если  , то
, то  . Т.к. f(x) – диф-ма, то
. Т.к. f(x) – диф-ма, то  .
.
По св-ву сохранения знака нестрогого нер-ва при предельном переходе :  .
.
(2 дост.- по т. Лагранжа).
Предел числовой последовательности. Сформулировать признак сходимости монотонной последовательности. Доказать теорему о единственности предела.
Число а называется пределом числовой последовательности  при
при  если для любого Е>0 существует натуральное число N(E), такое, что для любых n>N(E) выполняется условие
если для любого Е>0 существует натуральное число N(E), такое, что для любых n>N(E) выполняется условие  , записывают
, записывают  .
.
|
|
|

Числовая последовательность  монотонно не убывает (не возрастает) при
монотонно не убывает (не возрастает) при  , если для
, если для  выполнено
выполнено  .
.
Признак: если числовая последовательность  при
при  , монотонно не убывает (не возрастает) и ограничена сверху (снизу) числом A (B), тогда она сходится и её предел не больше, чем A (не меньше, чем B)
, монотонно не убывает (не возрастает) и ограничена сверху (снизу) числом A (B), тогда она сходится и её предел не больше, чем A (не меньше, чем B)
Если последовательность  , при
, при  имеет конечный предел, то он единственный .
имеет конечный предел, то он единственный .
Доказательство: Пусть  имеет 2 предела a и b при
имеет 2 предела a и b при  . Пусть для определённости a>b
. Пусть для определённости a>b  .
.
 ;
;
 .
.
N=max(N1;N2) 
 эти неравенства выполняются одновременно, чего быть не может, т.к. по определению E окрестность точки а содержит все члены последовательности, и E окрестность точки b содержит все члены последовательности
эти неравенства выполняются одновременно, чего быть не может, т.к. по определению E окрестность точки а содержит все члены последовательности, и E окрестность точки b содержит все члены последовательности  все члены не могут быть одновременно в 2 окрестностях, т.к. они не пересекаются.
все члены не могут быть одновременно в 2 окрестностях, т.к. они не пересекаются.
Билет №7.
Доказать необходимое условие экстремума дифференцируемой функции.
Для того, чтобы функция, дифференцируемая в точке  , имела локальный экстремум необходимо, чтобы производная в этой точке
, имела локальный экстремум необходимо, чтобы производная в этой точке  была равна 0.
была равна 0. 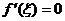
Доказательство: следует из теоремы Ферма.
Дано: точка  – точка локального экстремума.
– точка локального экстремума.
Доказать:  .
.
Согласно определению локального экстремума, функция принимает в  либо максимальное, либо минимальное значение
либо максимальное, либо минимальное значение  по теореме Ферма производная в точке
по теореме Ферма производная в точке  равна 0.
равна 0.
Т. Ферма:
Пусть y=f(x) определена на (a;b) и в некоторой точке этого интервала принимает наибольшее или наименьшее значение. Если в этой точке функция имеет производную, то эта производная равна нулю.
Доказательство: (Для наибольшего значения). Пусть  так как функция дифференцируема в
так как функция дифференцируема в 
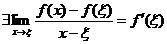 .
.  ;
;  ; Т.к.
; Т.к.  .
.
Вывести 1 замечательный предел: 
 Пусть
Пусть 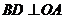 ,
,  .
.
Ясно, что  , но
, но


 , т.е.
, т.е.
 , т.к.
, т.к.  .
.
Билет №8-1.
Доказать теорему Бернулли-Лопиталя для предела отношения двух бесконечно малых функций.
Теорема. Пусть ф-ции f(x) и g(x) определены и дифференцируемы в  , представляют собой б.м.ф. при
, представляют собой б.м.ф. при  , причем
, причем  в
в  . Если
. Если  .
.
Доказательство: Рассмотрим {  . Доопределим по непрерывности данные функции нулем в точке a (f(a)=0, g(a)=0). Тогда на [a,
. Доопределим по непрерывности данные функции нулем в точке a (f(a)=0, g(a)=0). Тогда на [a,  ] функции f(x) и g(x) непрерывны, на (a;
] функции f(x) и g(x) непрерывны, на (a;  ) f(x) и g(x) дифференцируемы. По теореме Коши
) f(x) и g(x) дифференцируемы. По теореме Коши 
 при
при  по условию теоремы
по условию теоремы  >
>
Замечание 1: точка а может быть бесконечной, тогда  или
или  Формулировка: пусть f(x) b g(x) определены и дифференцируемы на
Формулировка: пусть f(x) b g(x) определены и дифференцируемы на 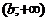 и представл. Б.м.ф. при
и представл. Б.м.ф. при  , причем
, причем  Если
Если 
Замечание 2: если  и
и  удовлетворяют всем условиям Б-Л и
удовлетворяют всем условиям Б-Л и  , то
, то  и т. д.
и т. д.
Билет №8-2.
Векторная функция скалярного аргумента:  и её производная. Касательная к пространственной кривой. Теорема о производной вектор-функции постоянной длины.
и её производная. Касательная к пространственной кривой. Теорема о производной вектор-функции постоянной длины.
Рассмотрим [a,b]. Пусть любому 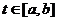 поставлен в соответствии некоторый вектор
поставлен в соответствии некоторый вектор  , тогда говорят, что на [a,b] задана векторная функция скалярного аргумента.
, тогда говорят, что на [a,b] задана векторная функция скалярного аргумента.
Пусть задана ортонормированная система координат с базисом  , тогда
, тогда 
Функции x(t), y(t), z(t)- скалярные функции действительного аргумента – координатные функции для вектор-функции  .
.
Геометрический смысл векторной функции:
 Функции
Функции  соответствует некоторая кривая
соответствует некоторая кривая
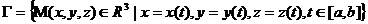
Такое представление кривой называют годографом.  называется пределом функции
называется пределом функции  скалярного аргумента при
скалярного аргумента при  если:
если:
 .
.
Рассмотрим приращение векторной функции, придадим t приращение  , тогда
, тогда
 .
.
Производной  в точке
в точке 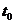 называется предел разностного отношения при
называется предел разностного отношения при 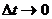
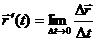 ,
,  .
.
 ,
,  .
.
 =
=
= 
Пусть  . Предельное положение секущей
. Предельное положение секущей  при
при  называют касательной к кривой Г в точке
называют касательной к кривой Г в точке  .
.  . Тогда при
. Тогда при  касательная в точке
касательная в точке  параллельна вектору
параллельна вектору  . Уравнение касательной:
. Уравнение касательной:  .
.

 - каноническое уравнение касательной.
- каноническое уравнение касательной.
Теорема: Пусть векторная функция скалярного аргумента  ,
,  - является непрерывно-дифференцируемой функцией на
- является непрерывно-дифференцируемой функцией на  , которой соответствует некоторая кривая Г:
, которой соответствует некоторая кривая Г:  . Тогда
. Тогда 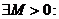 длина дуги Г удовлетворяет:
длина дуги Г удовлетворяет:  (при этом Г имеет конечную длину).
(при этом Г имеет конечную длину).
Доказательство: 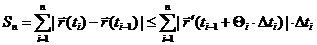 , где
, где 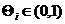 , по условию теоремы, функция непрерывно-дифференцируема, значит
, по условию теоремы, функция непрерывно-дифференцируема, значит  на отрезке
на отрезке  - непрерывная функция.
- непрерывная функция.  ,
,  (по 1 теореме Вейерштрасса).
(по 1 теореме Вейерштрасса).  при
при  .
.
Билет №9-1.
Формула Тейлора с остаточным членом в форме Пеано, Лагранджа.
Теорема. Пусть ф-ция F(x) определена в  и имеет в
и имеет в  производные до (n+1)-го порядка включительно. Пусть x – произвольное значение аргумента ф-ции из
производные до (n+1)-го порядка включительно. Пусть x – произвольное значение аргумента ф-ции из  , тогда для произвольного значения P, p>0
, тогда для произвольного значения P, p>0  , расположенная между a и x, такие что справедлива следующая формула:
, расположенная между a и x, такие что справедлива следующая формула:  .
.  . Формула называется формулой Тейлора с центром в точке a;
. Формула называется формулой Тейлора с центром в точке a;  - остаточный член в формуле Тейлора в общем виде.
- остаточный член в формуле Тейлора в общем виде.

 эта функция – многочлен степени n – многочлен Тейлора с центром в точке а.
эта функция – многочлен степени n – многочлен Тейлора с центром в точке а.
Обозначим  . Рассмотрим вспомогательную функцию
. Рассмотрим вспомогательную функцию  .
.
 , где
, где  Покажем, что на [a;x]
Покажем, что на [a;x]  удовлетворяет всем условиям теоремы Ролля:
удовлетворяет всем условиям теоремы Ролля:
1) непрерывность на [a;x];
2) дифференцируема на (a;x);
3) 
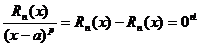
 ;
; 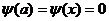 ;
; 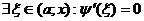


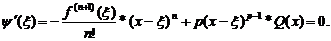
 ;
; 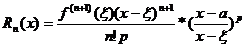
Теорема. Остаточный член в форме Тейлора представляет собой б. м. более высокого порядка малости, чем  при
при  .
.  ,
,  .
.
Доказать: 

 ;
;  =0;
=0;  ;
; 

 n раз применяем пр. Б-Л.=
n раз применяем пр. Б-Л.= 
Такую запись остаточного члена называют ост. Чл. В форме Пеано:  .
.
Рассмотрим другие формы записи остаточного члена.  ,
, 
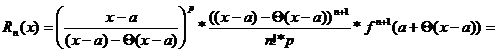

1) p=n+1, тогда  - остаточный член в форме Лагранжа.
- остаточный член в форме Лагранжа.
2) p=1 – в форме Коши:  Число
Число  в формуле Лагранжа и формуле Коши разные, т. К. зависят от P. Остаточный член в форме Лагранжа и Коши представляют собой погрешность, которую мы получаем, заменяя функцию f(x) ее многочленом Тейлора. Если нас интересует порядок малости такой замены при
в формуле Лагранжа и формуле Коши разные, т. К. зависят от P. Остаточный член в форме Лагранжа и Коши представляют собой погрешность, которую мы получаем, заменяя функцию f(x) ее многочленом Тейлора. Если нас интересует порядок малости такой замены при  , то он совпадает с порядком малости остаточного члена в форме Пеано.
, то он совпадает с порядком малости остаточного члена в форме Пеано.
Оценка остаточного члена в форме Лагранжа.
Пусть функция имеет производную любого порядка в  и эти производные ограничены одной и той же константой M.
и эти производные ограничены одной и той же константой M. 
 ;
; 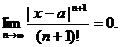
Билет №9-2.
Свойства б.м. функций.
1. Сумма конечного числа б.м.ф. при  представляет собой б.м. функцию при
представляет собой б.м. функцию при  .
.


 - б.м.ф.
- б.м.ф. 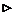
2. Произведение конечного числа б.м.ф. при  представляет собой б.м. функцию при
представляет собой б.м. функцию при  .
.


 - б.м.ф.
- б.м.ф. 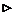
3. Пусть  - б.м.ф. при
- б.м.ф. при  , а
, а  - ограничена в
- ограничена в  , тогда
, тогда  - б.м.ф. при
- б.м.ф. при  .
.


 . Пусть
. Пусть  , тогда
, тогда  , для
, для  , тогда
, тогда  - б.м.ф. при
- б.м.ф. при  .
. 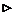
Билет №10.
Доказать первое достаточное условие экстремума функции.
Пусть функция  определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
Доказательство: Рассмотрим точку х из указанной окрестности, тогда на  :
:
1.  - непрерывна.
- непрерывна.
2. на  - дифференцируема.
- дифференцируема.
По т. Лагранжа  , где
, где  , т.к.
, т.к. 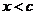 , то
, то 
на 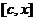 :
:  где
где  ,
, 
Дифференциал функции – определение, геометрический смысл. Доказать инвариантность формы дифференциала первого порядка.
Дифференциалом функции y=f(x) в точке называют главную линейную, относительно приращения аргумента, часть полного приращения функции в данной точке.
Инвариантность формы первого дифференциала.
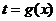 ;
;  , где Х – независимая переменная.
, где Х – независимая переменная. 
Билет №11.
Доказать второе достаточное условие экстремума.
Пусть ф-ция  определена и имеет в окрестности точки с производную до n-го порядка включительно, причем в самой точке с все производные до (n-1)-го порядка включительно равны 0, а n-ная производная в точке С отлична от нуля. Если n – четное, тогда С – точка локального экстремума, в частности, если
определена и имеет в окрестности точки с производную до n-го порядка включительно, причем в самой точке с все производные до (n-1)-го порядка включительно равны 0, а n-ная производная в точке С отлична от нуля. Если n – четное, тогда С – точка локального экстремума, в частности, если  , то x=c –локальный минимум, если
, то x=c –локальный минимум, если 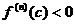 , то x=c –локальный максимум.
, то x=c –локальный максимум.
Доказательство: Запишем формулу Тейлора с остаточным членом в форме Пеано с центром в точке С.  , где
, где  -б.м.ф. при
-б.м.ф. при  . Пусть n – четное, тогда
. Пусть n – четное, тогда  не меняет знак при переходе через С.
не меняет знак при переходе через С. 
 в которой функция сохраняет знак своего предела.
в которой функция сохраняет знак своего предела.  ,
,  .
.  .
.  , если
, если 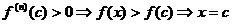 - точка локального экстремума.
- точка локального экстремума.
Доказать теорему о пределе произведения функций.
Пусть  и
и  при
при  имеют конечные пределы равные A и B соответственно, тогда
имеют конечные пределы равные A и B соответственно, тогда 
Дано: 
Доказательство:  ,
,  ,
,

Билет №12.
Доказать достаточное условие выпуклости графика функции.
Пусть  определена и дважды дифференцируема на
определена и дважды дифференцируема на  . Для того, чтобы график функции имел направление выпуклости вниз (вверх) достаточно, чтобы
. Для того, чтобы график функции имел направление выпуклости вниз (вверх) достаточно, чтобы  была неотрицательная (неположительная) на
была неотрицательная (неположительная) на  .
.
Доказательство:
Дано: 
Доказать:  - выпуклость вниз на
- выпуклость вниз на  .
.
Пусть  .
.
Уравнение касательной: 
 , где
, где  , если
, если  ,
, 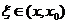 , если
, если  ,
,
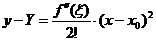 , т.к.
, т.к. 
 график функции
график функции  на
на  лежит не ниже касательной
лежит не ниже касательной 
 выпуклость вниз на
выпуклость вниз на  .
.
Доказать теорему о знакопостоянстве функции, имеющей отличный от нуля предел.
Если  , то существует окрестность точки а, в которой
, то существует окрестность точки а, в которой  и знак
и знак  совпадает со знаком значения b.
совпадает со знаком значения b.
Доказательство: по условию  , т.е.
, т.е.  , или
, или  справедливы неравенства
справедливы неравенства  .
.
Возьмём за  число
число  . Тогда
. Тогда  ,
,  ,
,  являются числами одного знака. Следовательно, в силу неравенства
являются числами одного знака. Следовательно, в силу неравенства  ,
,  и имеет знак числа b в указанной
и имеет знак числа b в указанной  -окрестности точки а.
-окрестности точки а.
Билет №13.
Необходимое и достаточное условие существования точки перегиба графика функции. Доказать необходимое условие.
Пусть функция  определена и дважды непрерывно-дифференцируема в окрестности точки С. Для того, чтобы (с,
определена и дважды непрерывно-дифференцируема в окрестности точки С. Для того, чтобы (с,  ), была точкой перегиба графика функции
), была точкой перегиба графика функции  , необходимо чтобы
, необходимо чтобы  .
.
Доказательство:
Дано: (с,  ) – точка перегиба.
) – точка перегиба.
Доказать:  .
.
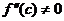 - это значит, согласно свойству непрерывности, что функция обладает знакопостоянством.
- это значит, согласно свойству непрерывности, что функция обладает знакопостоянством.
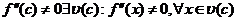 , т.е. в этой окрестности график функции имеет одинаковые направления выпуклости слева и справа от точки С, что противоречит определению точки перегиба
, т.е. в этой окрестности график функции имеет одинаковые направления выпуклости слева и справа от точки С, что противоречит определению точки перегиба  в точке С
в точке С  .
.
Доказать теоремы об эквивалентных бесконечно малых.
Теорема. Для того, чтобы б.м.ф.  и
и  при
при  были эквивалентными, при
были эквивалентными, при  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы  ,
,  .
.
Доказательство. Необходимость. Дано.  Доказать, что (
Доказать, что (  .
. 
Достаточность. Дано.  Доказательство.
Доказательство.  .
.
Рассмотрим сумму конечного числа б.м.ф.  , где
, где  - б.м.ф. при
- б.м.ф. при  .
.
Пусть  , k=2,3,….n тогда
, k=2,3,….n тогда  - главная часть б.м.ф.
- главная часть б.м.ф.
Билет №14.
Доказать теорему Коши.
Пусть функции f(x) и g(x): 1) определены и непрерывна на [a,b]; 2) дифференцируемы на интервале (a,b); 3) 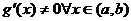 тогда
тогда  .
.
Доказательство: 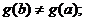 Вводим вспомогательную функцию
Вводим вспомогательную функцию  . Эта функция удовлетворяет всем условиям теоремы Ролля: 1)
. Эта функция удовлетворяет всем условиям теоремы Ролля: 1) 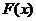 непрерывна на [a,b]; 2)
непрерывна на [a,b]; 2) 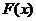 дифференцируема на (a,b); 3)
дифференцируема на (a,b); 3)  .
.
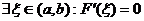 (по теор. Ролля).
(по теор. Ролля).  .
.  .
.
Вывести формулу для производной сложной функции.
Пусть функция  , дифф. В точке t=t0, а функция
, дифф. В точке t=t0, а функция  - дифференцируема в точке
- дифференцируема в точке  , тогда функция
, тогда функция 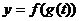 дифференцируема в точке t=t0, причем
дифференцируема в точке t=t0, причем  .
.
Док-во (должны доказать, что  ). Имеем, что
). Имеем, что  .
.  .
. 
 .
.
Билет №15.
Доказать достаточное условие возрастания дифференцируемой функции.
Для того, чтобы функция  , определённая и дифференцируемая на
, определённая и дифференцируемая на  , возрастала на
, возрастала на  , достаточно, чтобы
, достаточно, чтобы  на
на  .
.
Доказательство:
Дано: 
Доказать:  - возрастает на
- возрастает на 

1)  - определена
- определена
2)  - дифференцируемая.
- дифференцируемая.
Согласно т. Лагранжа  , т.к.
, т.к.  ,
,  - возрастает на
- возрастает на  .
.
Длина дуги плоской кривой. Производная и дифференциал длины дуги плоской кривой.
Рассмотрим в XOY плоскую кривую Г.

 ;
; 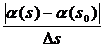 - Средняя кривизна кривой Г. Кривизной кривой Г в точке
- Средняя кривизна кривой Г. Кривизной кривой Г в точке  называют предел (если он существует) средней коивизны при
называют предел (если он существует) средней коивизны при  .
.  ;
;  ; Если
; Если  , то полагают
, то полагают 
Билет №16-1.
Формула Тейлора с остаточным членом в форме Пеано, Лагранджа.
Теорема. Пусть ф-ция F(x) определена в  и имеет в
и имеет в  производные до (n+1)-го порядка включительно. Пусть x – произвольное значение аргумента ф-ции из
производные до (n+1)-го порядка включительно. Пусть x – произвольное значение аргумента ф-ции из  , тогда для произвольного значения P, p>0
, тогда для произвольного значения P, p>0  , расположенная между a и x, такие что справедлива следующая формула:
, расположенная между a и x, такие что справедлива следующая формула:  .
.  . Формула называется формулой Тейлора с центром в точке a;
. Формула называется формулой Тейлора с центром в точке a;  - остаточный член в формуле Тейлора в общем виде.
- остаточный член в формуле Тейлора в общем виде.

 эта функция – многочлен степени n – многочлен Тейлора с центром в точке а.
эта функция – многочлен степени n – многочлен Тейлора с центром в точке а.
Обозначим  . Рассмотрим вспомогательную функцию
. Рассмотрим вспомогательную функцию  .
.
 , где
, где  Покажем, что на [a;x]
Покажем, что на [a;x]  удовлетворяет всем условиям теоремы Ролля:
удовлетворяет всем условиям теоремы Ролля:
- непрерывность на [a;x];
- дифференцируема на (a;x);
-

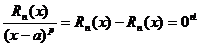
 ;
; 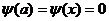 ;
; 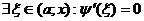


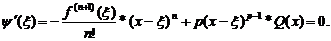
 ;
; 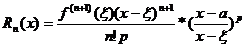
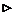
Теорема. Остаточный член в форме Тейлора представляет собой б. м. более высокого порядка малости, чем  при
при  .
.  ,
,  .
.
Доказать: 

 ;
;  =0;
=0;  ;
; 

 n раз применяем пр. Б-Л.=
n раз применяем пр. Б-Л.= 
Такую запись остаточного члена называют ост. чл. в форме Пеано:  .
.
Рассмотрим другие формы записи остаточного члена.  ,
, 
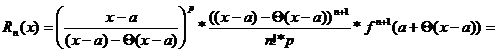

1) p=n+1, тогда  - остаточный член в форме Лагранжа.
- остаточный член в форме Лагранжа.
2) p=1 – в форме Коши:  Число
Число  в формуле Лагранжа и формуле Коши разные, т. к. зависят от P. Остаточный член в форме Лагранжа и Коши представляют собой погрешность, которую мы получаем, заменяя функцию f(x) ее многочленом Тейлора. Если нас интересует порядок малости такой замены при
в формуле Лагранжа и формуле Коши разные, т. к. зависят от P. Остаточный член в форме Лагранжа и Коши представляют собой погрешность, которую мы получаем, заменяя функцию f(x) ее многочленом Тейлора. Если нас интересует порядок малости такой замены при  , то он совпадает с порядком малости остаточного члена в форме Пеано.
, то он совпадает с порядком малости остаточного члена в форме Пеано.
Оценка остаточного члена в форме Лагранжа.
Пусть функция имеет производную любого порядка в  и эти производные ограничены одной и той же константой M.
и эти производные ограничены одной и той же константой M. 
 ;
; 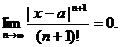
Билет №16-2.
Доказать непрерывность функций 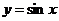 и
и 
1) 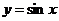
Зададим приращение аргумента функции 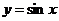 в точке X:
в точке X:

Здесь использовано неравенство  . Итак,
. Итак,  . Тогда
. Тогда  , т.е.
, т.е.  функция
функция 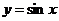 непрерывна в точке X, а т.к. точка X принадлежит R , т.е. произвольна, то можна сказать, что функция
непрерывна в точке X, а т.к. точка X принадлежит R , т.е. произвольна, то можна сказать, что функция 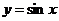 непрерывна на всей числовой оси.
непрерывна на всей числовой оси.
2)  ыв
ыв
Зададим приращение аргумента функции  в точке X:
в точке X:
 ,
,  - непрерывная функция.
- непрерывная функция.
Билет №17.
Доказать первое достаточное условие экстремума функции.
Пусть функция  определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
Доказательство: Рассмотрим точку X из указанной окрестности, тогда:
1. на 
 - непрерывна.
- непрерывна.
2. на  - дифференцируема.
- дифференцируема.
По т. Лагранжа  , где
, где  , т.к.
, т.к. 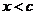 , то
, то 
на 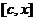 :
:  где
где  ,
, 
Непрерывность сложной функции.
Пусть  - непрерывна в точке x=a, а функция
- непрерывна в точке x=a, а функция  - непрерывна в точке b=f(a), тогда сложная функция z=g(f(x)) – непрерывна в точке x=a.
- непрерывна в точке b=f(a), тогда сложная функция z=g(f(x)) – непрерывна в точке x=a.
Доказательство: Т.к g(y) – непрерывна в точке y=b, то  , т.к. y=f(x) – непрерывна в точке x=a, то
, т.к. y=f(x) – непрерывна в точке x=a, то 
 .
.
Замечание: 
Билет №18.
Теорема о связи дифференцируемости и непрерывности.
Для того чтобы функция была дифференцируема в точке, необходимо, чтобы она была непрерывной в этой точке.
Дано:  - дифференцируема в точке.
- дифференцируема в точке.
Доказать:  - непрерывна в точке.
- непрерывна в точке.
 , где
, где  - б.м.ф. при
- б.м.ф. при  .
.
 - непрерывна в заданной точке.
- непрерывна в заданной точке.
Доказать теорему о пределе промежуточной функции.
Пусть функции  и
и  имеет конечный предел А при
имеет конечный предел А при  и пусть
и пусть  тогда
тогда 
Доказательство:
 ,
, 
 ,
, 


Рассмотрим  , начиная с некоторого номера N
, начиная с некоторого номера N  и
и  , будут одинакого выполняться
, будут одинакого выполняться  . Значит,
. Значит, 
Билет №19.
Доказать теорему Лагранжа.
Пусть функция  .
.
6. Определена и непрерывна на отрезке  .
.
7. Дифференцируема на интервале  .
.
Тогда существует  из интервала
из интервала  .
.
Доказательство: Рассмотрим вспомогательную функцию  , где
, где  - константа.
- константа.

3. Она непрерывна на 
4. дифференцируема на  .
.
Все условия теоремы Ролля выполняются  существует
существует  из
из 

Дифференциал функции – определение, геометрический смысл. Доказать инвариантность формы дифференциала первого порядка.
Дифференциалом функции y=f(x) в точке называют главную линейную, относительно приращения аргумента, часть полного приращения функции в данной точке.
Инвариантность формы первого дифференциала.
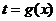 ;
;  , где Х - независимая переменная.
, где Х - независимая переменная. 
Билет №20.
Доказать теоремы Ролля и Ферма.
Пусть дана функция  .
.
8. Определена и непрерывна на отрезке  .
.
9. Дифференцируема на интервале  .
.
10. И на концах отрезка принимает одинаковые значения.
Тогда существует точка  , принадлежащая отрезку
, принадлежащая отрезку  .
.
Доказательство: Т.к. функция  непрерывна на отрезке
непрерывна на отрезке  , то согласно 2 теореме Вейерштрасса она достигает своего минимального и максимального значения.
, то согласно 2 теореме Вейерштрасса она достигает своего минимального и максимального значения.
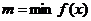 ,
,  ,
,
 ,
,  .
.
Случаи:
3.  ,
,  - любое из интервала
- любое из интервала 
4.  в силу 3-го условия теоремы, одно из значений минимального или максимального достигается функцией во внутренней точке отрезка
в силу 3-го условия теоремы, одно из значений минимального или максимального достигается функцией во внутренней точке отрезка  .
.
Согласно второму условию теоремы Ролля, функция дифференцируема на интервале  в любой точке, то по теореме Ферма существует
в любой точке, то по теореме Ферма существует  .
.
Т. Ферма:
Пусть y=f(x) определена на (a;b) и в некоторой точке этого интервала принимает наибольшее или наименьшее значение. Если в этой точке функция имеет производную, то эта производная равна нулю.
Доказательство: (Для наибольшего значения). Пусть 
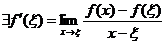 .
.  ;
;  ; Т.к.
; Т.к.  .
.
Доказать теорему о связи функции, её предела и бесконечно малой.
Для того, чтобы функция  , определённая в
, определённая в  имела конечный предел при
имела конечный предел при  , необходимо и достаточно чтобы эту функцию можно было представить в виде суммы предела и б.м.ф. при
, необходимо и достаточно чтобы эту функцию можно было представить в виде суммы предела и б.м.ф. при  (
( 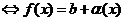 , где
, где  - б.м.ф. при
- б.м.ф. при  ).
).
Доказательство: I Необходимость:
Дано: 
Доказать: 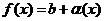 , где
, где  - б.м.ф. при
- б.м.ф. при  .
.

Пусть  по определению б.м.ф
по определению б.м.ф  - б.м.ф. при
- б.м.ф. при  .
.

II Достаточность:
Дано: 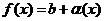 , где
, где  - б.м.ф. при
- б.м.ф. при  .
.
Доказать: 

Билет №21.
Формула Маклорена для 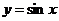 с остаточным членом в форме Пеано.
с остаточным членом в форме Пеано.
 , где
, где
1)  Пеано
Пеано
2)  где
где  - Лагранж
- Лагранж
3)  - Коши
- Коши
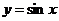 ,
,  ,
,  ,
, 
 (Пеано) , т.к. sin x - нечет., то вып. усл.:
(Пеано) , т.к. sin x - нечет., то вып. усл.: 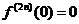
 ,
,  (Лагранж)
(Лагранж)
Сформулировать определение функции, непрерывной на отрезке. Основные теоремы о функциях, непрерывных на отрезке.
Функцию f(x) называют непрерывной на [a,b], если она непрерывна на (a,b) и непрерывна справа в точке x=a и непрерывна слева в точке x=b.
Первая теорема Вейерштрасса.
Если f(x) непрерывна на [a,b], то она ограничена на этом отрезке.  .
.
Вторая теорема Вейерштрасса.
Если f(x) непрерывна на [a,b], то она достигает на этом отрезке своего наименьшего (наибольшего) значения.
Первая теорема Больцано-Коши.
Функция  , тогда
, тогда 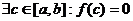
Доказательство: [a,b] разделим пополам и получим отрезки [a,a+b/2] и [a+b/2,b]. Из них выберем тот, на концах которого ф-ция принимает значения, разные по знаку и обозначим [a1,b1], f(a1)*f(b1)<0. С этим отрезком поступим так же. [a1,a1+b1/2] и [a1+b1/2,b1]. Выберем отрезок с разными по знаку концами. Когда-нибудь получим отрезок  .
.  . При
. При  ,
, 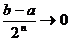 . Получим систему вложенных отрезков
. Получим систему вложенных отрезков  . Если при делении отрезка пополам значение функции в середине отрезка равно нулю, то теорему можно считать доказанной. Система вложенных отрезков, длина которых стремится к нулю, имеет одну общую точку => существует точка С. Докажем, что f(с)=0. Предположим, что
. Если при делении отрезка пополам значение функции в середине отрезка равно нулю, то теорему можно считать доказанной. Система вложенных отрезков, длина которых стремится к нулю, имеет одну общую точку => существует точка С. Докажем, что f(с)=0. Предположим, что  . Для определенности f(c)>0. Т.к. ф-ция непрерывна на отрезке [a,b], то она непрерывна в точке С. Раз f(c)>0, то
. Для определенности f(c)>0. Т.к. ф-ция непрерывна на отрезке [a,b], то она непрерывна в точке С. Раз f(c)>0, то  ;
;  - притиворечие, что и треб. доказ.
- притиворечие, что и треб. доказ.
Дата добавления: 2018-05-12; просмотров: 384; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
