Линейно-зависимые и линейно-независимые системы векторов

⇐ ПредыдущаяСтр 3 из 3

Пусть имеем векторное пространство V и систему векторов A={ } (система отличается от множества тем, что в ней могут быть одинаковые элементы). Вектор называется линейной комбинацией системы векторов A. Если все скаляры α₁ = α₂ = α₃... = α_k = 0, то такая комбинация называется тривиальной (простейшей), (и ). Если хотя б один скаляр отличен от 0, то такая комбинация называется нетривиальной.

Определение 1: система векторов A называется линейно-независимой, если только тривиальная линейная комбинация векторов системы равна , (т.е. Определение 2: система векторов A называется линейно-зависимой, если существует хотя бы одна нетривиальная линейная комбинация, равная .

Упражнения и примеры

На практике, чтобы установить линейную зависимость системы векторов, нужно, зачастую установить истинность высказывания Покажем, что A={ }-линейнонезависимая система.

Решение: α(1,0)+β(0,1)=(0,0) ↔ (α,0)+(0,β)=(0,0) ↔ α=0, β=0, следовательно, A линейно-независимая система.Покажем, что A={ } - линейно-зависимая система.

Решение. Найдём нетривиальную комбинацию, равную .

, т.е.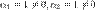

Элементами векторного пространства V являются линейные функции (т.е.вида y=kx+b). Установите, являются ли линейно-зависимыми (-независимыми) следующие системы: 1) A=(y=2x+3, y=x-√2) 2) B=( y=2x+12, y=x-√3, y=x+6)

ЭВКЛИДОВО ПРОСТРАНСТВО

Нормированные векторные пространстваПонятие абсолютного значения распространяется на векторные пространства над нормированным полем K. Нормой в векторном пространстве E называется отображение удовлетворяющее следующим аксиомам: 1) ;2) ;3) (неравенство треугольника).

Евклидово пространство Пусть E - векторное пространство над полем R. Отображение которое каждым двум элементам ставит в соответствие действительное число, обозначаемое символом , называетсяскалярным произведением, если и выполняются следующие аксиомы:1) 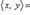;2) ;3) ;4) .Векторное пространство, в котором определено скалярное произведение, называется евклидовым пространством.Примеры

Наглядными примерами евклидовых пространств могут служить пространства: размерности 1 (вещественная прямая) размерности 2 (евклидова плоскость) размерности 3 (евклидово трехмерное пространство) Евклидово пространство можно считать современной интерпретацией и обобщением (так как оно допускает размерности больше трех) классической (Евклидовой) геометрии. Более абстрактный пример: пространство вещественных многочленов p(x) степени, не превосходящей n, со скалярным произведением, определенным как интеграл произведения по конечному отрезку (или по всей прямой, но с быстро спадающей весовой функцией, например )

Норма вектора

Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина

определяет квадрат длины вектора x. Для обозначения длины (называемой также нормой вектора) используется обозначение Например, Рис. 16 Норма вектора Вектор единичной длины (||x|| = 1) называется нормированным. Ненулевой вектор (x ≠ 0) можно нормировать, разделив его на длину, т.е. x = ||x|| (x/||x||) = ||x|| e. Здесь e =x/||x|| — нормированный вектор.Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.

Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы.

Формулировка

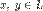Пусть дано линейное пространство L со скалярным произведением . Пусть — норма, порождённая скалярным произведением, то есть . Тогда для любых имеем:

причём равенство достигается тогда и только тогда, когда векторы x и y пропорциональны (коллинеарны).

[править]Комментарии

В конечномерном случае можно заметить, что , где — площадь параллелограмма, натянутого на векторы x и y.

В общем случае: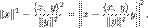

Нера́венство треуго́льника в геометрии, функциональном анализе и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Неравенство треугольника включается как аксиома в определение метрического пространства, нормы и т.д.; также, часто является теоремой в различных теориях. Пусть дан треугольник ΔABC. Тогда причём равенство | AC | = | AB | + | BC | достигается только тогда, когда треугольник вырожден, и точка B лежит строго между A и C.

Евклид в Началах доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного. Из неё выводится теорема о том, что против большей стороны треугольника лежит больший внутренний угол. Далее, методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. А из этой теоремы выводится неравенство треугольника.

азис e₁, e₂, … , e_n в n –мерном евклидовом пространстве E_n называется ортогональным, если (e_i, e_j) = 0 "i ≠ j , т.е. все векторы попарно ортогональны.

Ортогональный базис из единичных векторов называется ортонормированным.

Ортогонализация

Пусть и векторы составляют базис . Этот базис называется ортогональным если векторы попарно ортогональны: ; базис называется нормированным если каждый его вектор имеет единичную длину: ; базис называется ортонормированнымесли он ортогонален и нормирован, т.е.

Здесь — символ Кронекера.

Ортогональный базис будем обозначать .

В пространстве стандартным ортогональным базисом является базис, состоящий из векторов

Существование же ортогонального базиса в произвольном евклидовом пространстве еще требует доказательства. Предварительно установим следующий результат.

Теорема. Если ненулевые векторы попарно ортогональны, то они линейно независимы.

Доказательство. В самом деле, если

то, домножив это равенство скалярно на , получим

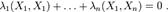
Поскольку для , то , откуда . Аналогично показывается, что и все остальные равны 0. ♦

Задача. Пусть имеется произвольная система линейно независимых векторов. Требуется построить систему ортогональных векторов такую, чтобы линейные оболочки любых подсистем совпадали:

Иными словами, вектор должен линейно зависеть от , вектор должен линейно выражаться через , — через и т.д.

Алгоритм ортогонализации Грама - Шмидта ⁵⁾

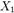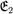В случае возьмем : поскольку вектор входит в линейно независимую систему , то . Далее, будем искать в виде

при пока неопределенном коэффициенте 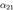. Очевидно, что при таком выборе условие будет выполнено. Подберем так, чтобы выполнялось .

Таким образом, коэффициент 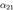, а вместе с ним и вектор определяются единственным образом. При этом , ибо, в противном случае, векторы и были бы л.з., что противоречит предположению о л.н.з. системы . Продолжаем процесс далее: вектор 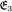ищем в виде

при пока неопределенных коэффициентах и 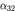. Условие выполняется поскольку

Подберем скаляры и так, чтобы выполнялось и . Два этих условия задают систему линейных уравнений

Процесс продолжается далее аналогично. Допустим, что векторы 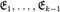уже построены, они ненулевые, попарно ортогональные и

Вектор ищем в виде:

при пока неопределенных коэффициентах . Условие выполнено и, кроме того, (в противном случае , т.е. система л.з. Коэффициенты подбираются из условий . Получающаяся система линейных уравнений имеет единственное решение