Теорема Остроградского-Гаусса
Теорема Остроградского-Гаусса одна из важнейших для практики теорем электродинамики. Доказанная в ней формула устанавливает связь между потоком векторного поля через замкнутую поверхность и источниками этого поля, находящимися в объёме, ограниченном этой поверхностью.
Краткая история. Теорема сформулирована французским математиком Лагранжем в 1762 году. Применительно к электрическому полю теорему доказал российский математик и механик Остроградский Михаил Васильевич в 1826 году, а в 1831 году опубликовал результаты, представив формулу в дифференциальной форме. Доказанная им теорема получила название основной теоремы электростатики в дифференциальной форме. Примерно одновременно с этим немецкий математик, астроном и физик Карл Гаусс разработал общий метод преобразования тройного интеграла к поверхностному на примере решения задач электродинамики, а затем в 1839 году получил результат в интегральной форме и опубликовал его.
Суть теоремы. Полное векторное поле в любой точке является векторной суммой (интегралом) вкладов всех источников. Однако, за исключением самых простых случаев, вычислить эту сумму, как поверхностный интеграл крайне сложно. Тогда как, пользуясь теоремой Остроградского-Гаусса, удается рассчитать гораздо проще и изящнее.
Приведем формулу Остроградского-Гаусса без доказательств, поскольку это задача интересна только математикам.
|
|
|
Формулировка задачи. Пусть в некоторой области трехмерного пространства V, ограниченной замкнутой кусочно-гладкой поверхностью S, задано непрерывно-дифференцируемого векторное поле 
. Тогда, как установлено ранее, поток векторного поля через внешнюю сторону замкнутой поверхности S равен поверхностному интегралу первого рода по поверхности S от скалярного произведения вектора нормали к этой поверхности и вектора-функции поля.
Формула Остроградского-Гаусса позволяет математически выразить поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность более простым интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью.
Формула Остроградского-Гаусса в инвариантной и координатной форме соответственно имеет следующий вид:
, и (17)
. (18)
Из этих выражений становится понятным, почему теорему Остроградского-Гаусса иногда называют терему о дивергенции.
Данная теорема расширяет понятие дивергенции для конечного объема. Произведение 
дает мощность источников в элементарном объеме dV, поэтому полная мощность источников поля в объеме V определяется объемным интегралом в правой части формулы (17) или (18). Поток через замкнутую поверхность состоит из суммы входящего и выходящего потоков (точнее из разности выходящего и входящего из-за противоположных направлений нормалей к S). Итоговый поток будет положительным, если в объеме преобладают источники поля, и отрицательным, если преобладают «стоки». Следовательно, выходящий наружу поток равен интегральной мощности источников в объеме V.
|
|
|
Таким образом, формула (23) позволяет свести задачу вычисления поверхностного интеграла второго рода по замкнутой поверхности S к более простой: вычислению тройного интеграла по области V.
Основная ценность теоремы в области электродинамики состоит в том, что она позволяет глубже понять природу электростатического поля и устанавливает более общую связь между зарядами и полем. Она представляет собой более общую и более изящную формулировку закона Кулона.
Обобщением формулы Остроградского является формула Стокса для многообразий с краем, т.е. для замкнутых полупространств с границей.
Теорема Кельвина-Стокса
Другой не менее важной теоремой электродинамики является теорема Кельвина-Стокса, которую применительно к электродинамики часто, не совсем заслужено, называют теоремой Стокса. Данная теорема в обобщенном виде называется теоремой об интегрировании дифференциальных форм. В частотном случае теорема позволяет рассчитывать циркуляцию вектора по контуру конечной длины с помощью ротора этого вектора.
|
|
|
Историческая справка. Формула, устанавливающая данную взаимосвязь, была получена в 1949 году британским математиком и физиком Уильямом Томсоном лордом Кельвин. Тогда как, английским математиком, механиком и физиком-теоретиком ирландского происхождения Джорджем Стоксом она использовалась в качестве задачи на олимпиадах, проводимых в Кембриджском университете, а также была включена в обобщенную теорему в качестве частного случая. Стоит отметить, что главный приз за 1854 год достался 23-летнему английскому математику Джеймсу Максвеллу, который в последствие заложил основы электродинамики (уравнения Максвелла). Есть основания считать, что оно справился с этой теоремой. Вместе с тем, первое доказательство формулы Стокса было опубликовано только в 1861 году немецким математиком Германом Ганкелем.
Теорема Кельвина-Стокса позволяет рассчитывать циркуляцию вектора по контуру конечной длины с помощью ротора этого вектора.
|
|
|
Формулировка теоремы: Циркуляция векторного поля по замкнутому положительно ориентированному контуру L (т.е. направление нормали выбрано) равна потоку ротора этого поля через любую гладкую поверхность S, опирающуюся (натянутую) на данный контур.
Формула Кельвина-Стокса в инвариантной и координатной форме соответственно имеет следующий вид:
, и (19)
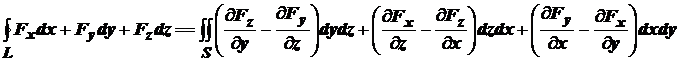. (20)
Для доказательства теоремы рассмотрим контур ABCA с охватываемой им площадью S (см. рис. 6). Весь контур разбивается на элементарные контуры той же ориентации AB0A, A0CA, BC0B, площадь которых равна dS.
Рис. 6 – Пояснение к криволинейному интегрированию
Для вычисления интеграла по контуру ABCA, воспользуемся свойством аддитивности криволинейного интеграла второго рода, и представим интеграл по замкнутому контуру ABCA в виде суммы интегралов по контурам AB0A, BC0B и CA0C, лежащим в координатных плоскостях (см. рис. 6).
/
Легко убедиться что это действительно так, поскольку отрезки А0, В0 и С0 вносят нулевой вклад в суммарную циркуляцию, т.к. интегрирование по ним производится дважды, по в противоположных направлениях, следовательно циркуляция всех этих внутренних участков взаимно компенсируется. Некомпенсированными остаются только внешние участки принадлежащие контуру АВСА (контуру L в общем виде), что в итоге и дает формулу Кельвина-Стокса.
Формулы (19) и (20) позволяют свести вычисление более сложного криволинейного интеграла второго рода к вычислению более простого двойного интеграла по поверхности S.
Доказательство формулы Кельвина-Стокса, строго подтверждает критерий потенциальности полей, согласно которому необходимым и достаточным условием (критерием) того, что векторное поле является потенциальным, оказывается тождественное равенство нулю его ротора.
Частным случаем теоремы Кельвина-Стокса является теорема Грина, устанавливающая связь между криволинейным интегралом по замкнутому контуру и двойным интегралом по односвязной области, ограниченной этим контуром. Теорема названа в честь английского математика Джорджа Грина.
Формула Кельвина-Стокса находит широкое применение в гидро- и аэродинамике, электродинамике и т.д.
Заключение
Итак, в ходе лекции рассмотрены дифференциальные операции в скалярных и векторных полях, раскрыта сущность таких дифференциальных операторов, как градиент, лапласиан, дивергенция и ротор, приведен их физический смысл.
Векторные операторы ротор и дивергенция наиболее часто применяются для векторных полей, тогда как градиент и лапласиан – для скалярных полей.
Приведённая ниже таблица содержит все данные, относящиеся к дифференциальным операциям над векторными и скалярными полями.
Рассмотернные в лекции основные теоерем электродинамики Остроградского-Гаусса и Кельвина-Стокса имеют большую практическую значимость, поскольку сводят сложные задачи вычисления соответственно поверхностного интеграла и криволинейного интегралов второго рода к вычислению более простых интегралов.
Дата добавления: 2018-05-12; просмотров: 1531; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!