Задача линейного программирования
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ “МИСИС”
Кафедра БИСУП
Курсовая работа на тему:
Математические методы в экономике
Вариант: 16
Выполнила: студентка гр. МИБ-11-1
Мельникова Т.М.
Преподаватель:
Литвин И.З.
Москва 2011
Содержание
Введение………………………………………………………………………………………....3
1 Модель межотраслевого баланса…..………………….. …………………………………….4
2 Задача линейного программирования…………………………………………………….....7
3 Транспортная задача………………….....................................................................................17
3 Задача о назначениях…………………....................................................................................23
3 Решение игр………………….................................................................................................. 27
3 Игры с природой…………………...........................................................................................30
Выводы………………….............................................................................................................33
Литература……………………………………………………………………….................…...34
Введение
Математические методы являются важнейшим инструментом анализа экономических явлений и процессов, построения теоретических моделей, позволяющих отобразить существующие связи в экономической жизни, прогнозировать поведение экономических субъектов и экономическую динамику.
|
|
|
Одним из самых перспективным направлений в математических методах в экономике на данный момент является экономико-математическое моделирование с использованием комплексных переменных.
Математика как основа теории принятия решений широко применяется для управления (планирования, прогнозирования, контроля) экономическими объектами и процессами.
Целью курсовой работы являетсяподготовить слушателя к самостоятельному проведению бизнес-операционного исследования, основными этапами которого являются построение математической модели, решение управленческой задачи и анализ практических результатов.
В процессе написания курсовой работы будут решены следующие задачи:
1. Приобретение практических навыков построения экономико-математических моделей
2. Обучение применению компьютерных технологий при решении задач
3. Обучение постановке экономической задачи и переводу ее на математический язык.
Модель межотраслевого баланса
Задана таблица межотраслевого баланса:
| Производящие отрасли | Потребляющие
отрасли | Валовый продукт Х | Конечный продукт У | |||||
| 1 | 2 | 3 | 4 | |||||
| Металлургия | 30 | 30 | 50 | 35 | 205 | 60 | ||
| Нефтехимия | 25 | 50 | 40 | 42 | 182 | 25 | ||
| Оборонка | 30 | 40 | 35 | 50 | 190 | 35 | ||
| Машиностроение | 30 | 50 | 50 | 35 | 205 | 40 | ||
- составить матрицу прямых затрат
- проверить ее продуктивность
- рассчитать валовый продукт, соответствующий увеличению конечного продукта на (0,5V = 0,5 * 16 = 8) 8 %.
- расчеты выполнить в среде EXCEL.
1. Требуется найти совокупный продукт (Х=?), при котором конечный продукт достигнет уровня
Y=  =
= 
2. Матрица прямых продуктивных затрат имеет следующий вид:
30/205; 30/182; 50/190; 35/205
А = 25/205; 50/182; 40/190; 42/205
30/205; 40/182; 35/190; 50/205
30/205; 50/182; 50/190; 35/205
А = 
Матрица продуктивна, если наибольшая из сумм элементов в столбцах не превосходит единицы, причем для хотя бы одного столбца сумма меньше единицы => матрица А продуктивна.
Анализ таблицы приводит к следующей системе балансовых соотношений:
Система балансовых соотношений:
x1 = a11 x1 + a12 x2 +… a1n xn + y1
x2 = a21 x1 + a22 x2 +… a2n xn + y2 (1)
|
|
|
…………………………………..
xn = an1 x1 + an2 x2 +… ann xn + yn
В матричной форме:
x = Ax + y, где  ,
,
А- матрица прямых материальных затрат.
Из матричного уравнения сразу следует:
x = (E – A)-1 y (2)
Правую часть формулы (2) удобно вычислить в EXCEL:
1. Выделить диапазон ячеек для размещения обратной матрицы.
2. На верхней панели нажать f x.
3. Выбрать функцию МОБР в категории Математические.
4. Указать диапазон ячеек, в которых размещена матрица Е-А.
5. Нажать клавиши CTRL + SHIFT + ENTER
6. Записать результат.
Чтобы умножить полученную обратную матрицу на вектор у нужно
1. Выделить диапазон ячеек для размещения результатов умножения.
2. На верхней панели нажать f x.
3. Выбрать функцию МУМНОЖ в категории Математические.
4. Указать диапазоны ячеек, в которых размещены матрица (Е-А)-1 и у.
6. Нажать клавиши CTRL + SHIFT + ENTER
В результате расчетов в среде Excel получается следующее:

Рисунок 1 – Решение задачи в среде Excel
Таким образом,
Х = 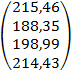
Это означает, что чтобы обеспечить требуемый конечный продукт, металлургия должна произвести совокупный продукт в объеме  , нефтехимия -
, нефтехимия -  , оборонка -
, оборонка -  , машиностроение -
, машиностроение -  .
.
|
|
|
Задача линейного программирования
Менеджеру производственной фирмы требуется составить оптимальный по прибыли план выпуска запчастей двух видов, используя для этого ресурсы трех типов. Их запасы ограничены значениями в1, в2, в3 соответственно. Пусть а11, а12 количество ресурсов первого типа, расходуемых на запчасти каждого вида, соответственно. Аналогичный смысл имеют символы а21, а22 и а31, а32.
Ожидаемая прибыль от реализации одной запчасти каждого вида составляет с1, с2 условных единиц, соответственно.
Требуется:
а) записать условия задачи в таблицу стандартной формы;
б) решить задачу табличным симплекс- методом
в) решить задачу в среде EXCEF
г) составить и решить двойственную задачу.
Исходные данные:
а) Условия задачи в таблице стандартной формы:
| Ресурсы | Запасы | Расх. коэфф. | |
| 1 | 2 | ||
| Количество ресурсов I типа | 268 | 12 | 4 |
| Количество ресурсов II типа | 120 | 4 | 4 |
| Количество ресурсов III типа | 252 | 3 | 12 |
| Прибыль, у.е. | - | 30 | 40 |
б) Решить задачу табличным симплекс-методом
Пусть х1, х2, х3 – количество изделий каждого вида.
12х1 + 4х2 ≤ 268
4х1 + 4х2 ≤ 120
3х1 + 12х2 ≤ 252
х1, х2 ≥ 0
F= 30х1 + 40х2 → max
1. Система ограничений должна быть приведена к каноническому виду.
К левой части неравенства 1 системы ограничений следует прибавить неотрицательную переменную х3 – чтобы преобразовать неравенство 1 в равенство.
К левой части неравенства 2 системы ограничений следует прибавить неотрицательную переменную х4 - чтобы преобразовать неравенство 2 в равенство.
К левой части неравенства 3 системы ограничений следует прибавить неотрицательную переменную х5 - чтобы преобразовать неравенство 3 в равенство.
12х1 + 4х2 + х3 = 268
4х1 + 4х2 + х4 = 120
3х1 + 12х2 + х5 = 252
Система ограничений приведена к каноническому виду, т.е. все условия системы представляют собой уравнения.
Определимся с начальным опорным решением.
Наличие единичного базиса в системе ограничений позволяет легко найти начальное опорное решение. Рассмотрим подробнее:
Переменная x3 входит в уравнение 1 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. х3 - базисная переменная.
Переменная x4 входит в уравнение 2 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. х4 - базисная переменная.
Переменная x5 входит в уравнение 3 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. х5 - базисная переменная.
Переменные, которые не являются базисными называются свободными переменными. Приравняв свободные переменные нулю в получившийся системе ограничений мы получим начальное опорное решение.
X н = ( 0 , 0 , 268 , 120 , 252 )
Вернемся к функции F.
F = 30х1 + 40х2 → max
Функция F не содержит базисных переменных.
Для составления начальной симплекс таблицы выполнены все условия.
В процессе дальнейших преобразований возможны два случая. Если в симплекс таблице, на каком то шаге, можно получить строку F состоящую из неотрицательных элементов - задача решена, найдено оптимальное решение. В противном случае - функция не является ограниченной.
При составлении исходной симплекс таблицы, коэффициенты при переменных функции F записываются с противоположными знаками, а свободный член со своим знаком.
1. Составляется исходная симплекс-таблица:
| Базисные переменные | х1 | х2 | x3 | x4 | x5 | Свободные члены | Отношение |
| x3 | 12 | 4 | 1 | 0 | 0 | 268 | 268/4=67 |
| x4 | 4 | 4 | 0 | 1 | 0 | 120 | 120/4=30 |
| x5 | 3 | 12 | 0 | 0 | 1 | 252 | 252/12=21 |
| F | -30 | -40 | 0 | 0 | 0 | 0 |
За ведущий выбирается столбец 2 , так как -40 - наименьший элемент в F строке. Элемент F строки, принадлежащий столбцу свободных членов не рассматриваем.
За ведущую выбирается строка 3, так как отношение свободного члена к соответствующему элементу выбранного столбца для 3 строки является наименьшим. Отношение вычисляется только для положительных элементов столбца 3.
Разделим элементы ведущей строки на 12:
| Базисные переменные | х1 | х2 | x3 | x4 | x5 | Свободные члены |
| x3 | 12 | 4 | 1 | 0 | 0 | 268 |
| x4 | 4 | 4 | 0 | 1 | 0 | 120 |
| x5 | 1/4 | 1 | 0 | 0 | 1/12 | 21 |
| F | -30 | -40 | 0 | 0 | 0 | 0 |
От элементов строки 1 нужно отнять соответствующие элементы строки 3, умноженные на 4.
От элементов строки 2 нужно отнять соответствующие элементы строки 3, умноженные на 4.
От элементов строки F нужно отнять соответствующие элементы строки 3, умноженные на - 40.
| Базисные переменные | х1 | х2 | x3 | x4 | x5 | Свободные члены |
| x3 | 11 | 0 | 1 | 0 | -1/3 | 184 |
| x4 | 3 | 0 | 0 | 1 | -1/3 | 36 |
| x2 | 1/4 | 1 | 0 | 0 | 1/12 | 21 |
| F | -20 | 0 | 0 | 0 | 10/3 | 840 |
х2 = ( 0 , 21 , 184 , 36 , 0)
F = 840 = 20 х1 -10/3 х5
Значение функции F для данного решения: F (х2) = 840
2. За ведущий выберем столбец 1 , так как -20 наименьший элемент в F строке. Элемент F строки, принадлежащий столбцу свободных членов не рассматривается.
За ведущую выберается строку 2, так как отношение свободного члена к соответствующему элементу выбранного столбца для 2 строки является наименьшим. Отношение вычисляется только для положительных элементов столбца 2
| Базисные переменные | х1 | х2 | x3 | x4 | x5 | Свободные члены | Отношение |
| x3 | 11 | 0 | 1 | 0 | -1/3 | 184 | 184/11=16,7 |
| x4 | 3 | 0 | 0 | 1 | -1/3 | 36 | 36/3=12 |
| x2 | 1/4 | 1 | 0 | 0 | 1/12 | 21 | 21/0,25=84 |
| F | -20 | 0 | 0 | 0 | 10/3 | 840 | - |
Можно разделить элементы строки 2 на 3.
| Базисные переменные | х1 | х2 | x3 | x4 | x5 | Свободные члены |
| x3 | 11 | 0 | 1 | 0 | -1/3 | 184 |
| x4 | 1 | 0 | 0 | 1/3 | -1/9 | 12 |
| x2 | 1/4 | 1 | 0 | 0 | 1/12 | 21 |
| F | -20 | 0 | 0 | 0 | 10/3 | 840 |
От элементов строки 1 отнимаются соответствующие элементы строки 2, умноженные на 11.
От элементов строки 3 отнимаются соответствующие элементы строки 2, умноженные на 1/4.
От элементов строки F отнимаются соответствующие элементы строки 2, умноженные на -20.
| Базисные переменные | х1 | х2 | x3 | x4 | x5 | Свободные члены |
| x3 | 0 | 0 | 1 | -11/3 | 8/9 | 52 |
| x1 | 1 | 0 | 0 | 1/3 | -1/9 | 12 |
| x2 | 0 | 1 | 0 | -1/12 | 1/9 | 18 |
| F | 0 | 0 | 0 | 20/3 | 10/9 | 1080 |
Таким образом, F = 1080
F = 20/3 x4 +10/9 x5
Значение функции F для данного решения: F (X 1) = 1080
Учитывая, что все x i ≥ 0, по условию задачи, наибольшее значение функции F равно свободному члену 1080, т.е. мы получили оптимальное решение.
X опт = (12 , 18 , 0 , 0 , 0 )
в) решить задачу в среде EXCEL
Для того, чтобы решить задачу в среде Excel, следует воспрользоваться программой «Поиск решения».
Ввод исходных значений в соответствии с рисунком 2.

Рисунок 2 – Исходные значения к задаче линейного программировании
После этого устанавливаются необходимые ограничения в программе «Поиск решения» и получаются следующие результаты в соответствии с рисунком 3.
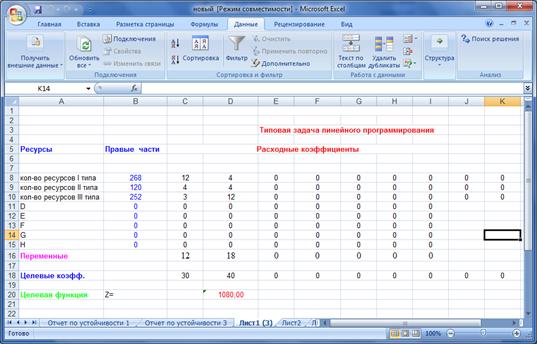
Рисунок 3 – Результат вычислений
Таким образом, видно, что результаты вычислений в среде Excel полностью совпадают с результатами табличных вычислений
г) Составить и решить двойственную задачу
Для составления двойственной задачи следует вернуться к исходной:
12х1 + 4х2 + 4х3 ≤ 268 12у1 +4у2 + 3у3 ≥ 30
4х1 + 4х2 + 4х3 ≤ 120 4у1 +4у2 + 12у3 ≥ 40
3х1 + 12х2 + 3х3 ≤ 252
х1, х2 ≥ 0 у1, у2, у3 ≥ 0
F= 30х1 + 40х2 → max G = 268y1 + 120 у2 + 252 у3 → min
Напоминание: х опт = (12,18), Fmax = 1080
1) Из любого ограничения двойственной задачи следует, что размерность уi совпадает с размерностью правой части (рубли/ ед. ресурса). Поэтому уi имеют смысл цены единицы ресурса. Их так и называют – теневые цены ресурсов.
Сравнивая теневые цены ресурсов можно решить, в какой из них выгоднее вкладывать дополнительные средства.
Выше было отмечено, что у1 = 2/3, у2=10/3. Таким образом, дополнительные средства выгоднее вкладывать в закупку сырья.
3) Так как х1 > 0 и х2 > 0, то
12у1 +4у2 + 3у3 = 30
4у1 +4у2 + 12у3 = 40
А так как первое ограничение исходной задачи обращается при оптимальном решении в строгое неравенство, то у1 = 0.
Итак, у2 =20/3, у3 =10/9.→ уопт = (0, 20/3, 10/9)
2) Fmax = 1080, Gmin =0*268 + 120* (20/3) + 252* (10/9) = 1080.
Таким образом, пункт а) теоремы двойственности выполнен
4) Можно подчеркнуть, что у1 = 0 означает не дефицитность первого ресурса,
у2 =20/3, у3 =10/9 - дефицитность последних двух ресурсов.
Транспортная задача
Торговый дом имеет четыре супермаркета, расположенные в четырех районах P, Q, R, S. Поставки продукции в эти супермаркеты осуществляются с двух, всегда полностью заполненных, складов А и В, площади которых вмещают по 40 контейнеров.
Прогнозирование спроса, выполненное службой маркетинга, показывает, что потребность супермаркетов в продукции в скором времени составит 50, 25, 30 и 35 контейнеров в день, соответственно.
Поэтому, планируется построить третий склад, который также всегда будет полностью заполнен и площадь которого вместит 60 контейнеров.
В таблице 1 приведены транспортные затраты (в руб.), соответствующие перевозкам одного контейнера со складов А и В и нового склада в каждый из супермаркетов. При этом рассматриваются два варианта размещения нового склада.
Менеджеру торгового дома требуется выбрать и обосновать оптимальный вариант размещения нового склада. Указать соответствующие оптимальные затраты. Результаты представить в графической форме.
Решить в среде EXCEL.
Среди задач линейного программирования особое место занимает транспортная задача. Ее методы широко используются в экономике и бизнесе, особенно в транспортных и дистрибьютерских фирмах.
Традиционная постановка транспортной задачи такова:

Имеются m поставщиков и n потребителей. У поставщиков сосредоточен однородный груз в количестве a1, a2,…..am.
Спрос потребителей на груз: в1, в2,….вn.
Известны стоимости (тарифы) сij на перевозку единицы груза от i-го поставщика к j- му потребителю.
Требуется составить оптимальный план перевозок грузов такой, чтобы:
1. вывести весь груз поставщиков
2. удовлетворить весь спрос потребителей
3. минимизировать суммарные затраты.
Построение математической модели:
Пусть хij – количество груза, перевозимого от i-го исх. пункта к j-му пункту потребления.
х11 + х12+ ….+х1n= а1
х21 + х22+ ….+х2n= а2 →все грузы должны быть вывезены
……………………..
хm1 + хm2+ ….+хmn= аm
х11 + х21+ ….+хm1= b1
х12 + х22+ ….+хm2= b2 → весь спрос удовлетворен
…………………….
х1n + х2n+ ….+хmn= bn
F = 
Таблица 1 – Транспортные затраты
| Склад | P | Q | R | S |
| A | 70 | 85+ 16 | 55- 16 | 120 |
| B | 110-16 | 90 | 75 | 110+ 16 |
| С (вариант 1) | 115 | 115- 16 | 70 | 90 |
| D (вариант 2) | 135 | 95 | 80 | 75+ 16 |
| Склад | P | Q | R | S |
| A | 70 | 101 | 39 | 120 |
| B | 94 | 90 | 75 | 126 |
| С (вариант 1) | 115 | 99 | 70 | 90 |
| D (вариант 2) | 135 | 95 | 80 | 91 |
Таблица 2 – Первый вариант размещения нового склада
| Пост. | 1 | 2 | 3 | 4 | ЗАПАСЫ |
| Потр. | |||||
| 1 | 70 | 101 | 39 | 120 | 40 |
| 2 | 94 | 90 | 75 | 126 | 40 |
| 3 | 115 | 99 | 70 | 90 | 60 |
| СПРОС | 50 | 25 | 30 | 35 | 140 |
Таблица 3 – Второй вариант размещения нового склада
| Пост. | 1 | 2 | 3 | 4 | ЗАПАСЫ |
| Потр. | |||||
| 1 | 70 | 101 | 39 | 120 | 40 |
| 2 | 94 | 90 | 75 | 126 | 40 |
| 3 | 135 | 95 | 80 | 91 | 60 |
| СПРОС | 50 | 25 | 30 | 35 | 140 |
Так как  , следовательно, задача – закрытая. Доказано, что закрытая транспортная задача всегда имеет оптимальное решение.
, следовательно, задача – закрытая. Доказано, что закрытая транспортная задача всегда имеет оптимальное решение.
Для решения задачи нужно воспользоваться функцией Excel «Поиск решения».

Рисунок 4 – Исходные данные для задачи с размещением первого склада

Рисунок 5 – Результат для задачи с размещением первого склада
Хопт = 
Общие затраты на доставку всей продукции, для оптимального решения, составляют 11205 ден. ед.

Рисунок 6 – Исходные данные для задачи с размещением второго склада

Рисунок 7 – Результат для задачи с размещением второго склада
Хопт = 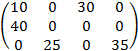
Общие затраты на доставку всей продукции, для оптимального решения, составляют 11190 ден. ед.
Таким образом, менеджеру компании предпочтительнее выбрать второй вариант размещения склада, т.к. там меньше общие затраты.
Задача о назначениях
Задана матрица затрат:
С = 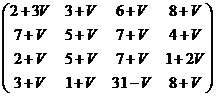
С =  =
= 
Известны затраты с i j , связанные с выполнением i-м кандидатом j - й работы. Предполагается, что каждый кандидат может быть назначен только на одну работу и каждая работа может быть выполнена только одним кандидатом.
Требуется так распределить (назначить) кандидатов на работы, чтобы суммарные затраты были минимальны.
Построение математической модели:
хi j =1, если i -й кандидат назначен на j- ю работу
хi j =0, в противном случае.
По условию:

Легко увидеть, что модель соответствует модели транспортной задачи, однако специальная форма записи модели позволила разработать более эффективный алгоритм (венгерский метод).
Теперь можно воспользоваться функцией «Поиск решения». Для этого следует ввести данные платежной матрицы, в поле «Запасы» и «Заказы» следует ввести единицы в соответствии с заданной моделью в соответствии с рисунком 8.

Рисунок 8 – Исходные данные к задаче о назначениях
После обработки данных получены следующие результаты в соответствии с рисунком 9.
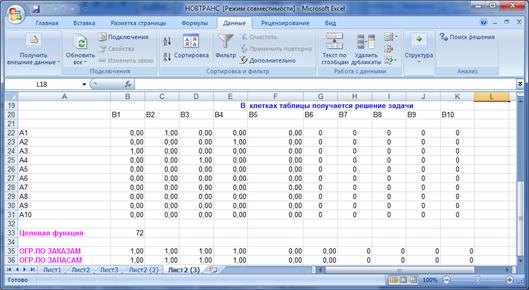
Рисунок 9 – Результат задачи о назначениях
Таким образом, оптимальная матрица назначений имеет следующий вид:

Минимальное значение целевой функции Fmin = 72
Графически данную задачу можно представить в соответствии с рисунком 10.
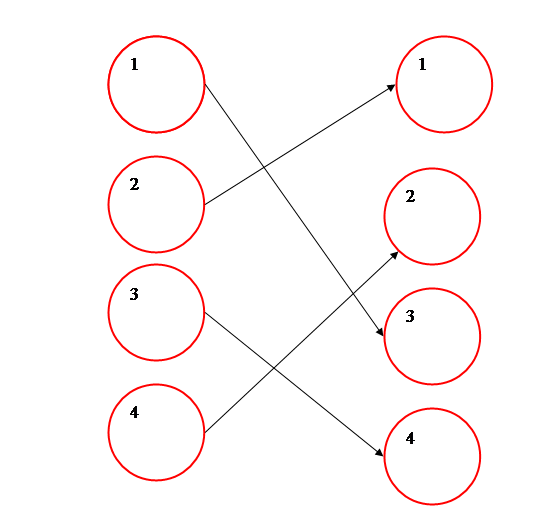
Рисунок 10 – Результат задачи о назначениях
Решение игр
Решить игру, заданную платежной матрицей, используя сведение к двойственным задачам линейного программирования:


Решение: max{7,11,13)=13
min {19,14,19)=19
Пусть (р1, р2, р3) – смешанная стратегия игрока А, (q1, q2, q3) – смешанная стратегия игрока В.
Напомним, что суммы вероятностей равны 1.
Для игрока А:
18р1 +19 р2 +15 р3≥ v
11р1 +14 р2 +13 р3≥ v
7р1 +11 р2 +19 р3≥ v
F = v → max
Преобразуем ограничения, разделив все члены неравенств на v (обозначим y1 = р1/v, y2 = р2/v, y3 = р3/v заметим, что v = 1/(y1 + y2+ y3)).
18y1 +19 y2 +15 y3≥ 1
11y1 +14 y2 +13 y3≥1
7y1 +11y2 +19 y3≥ 1
F = y1+ y2+ y3→ min
Для игрока B:
18q1 + 11q2 +7q3 ≤ v
19q1 + 14q2 +11q3 ≤ v
15q1 + 13q2 +19q3 ≤ v
F = v → min
Преобразуем ограничения, разделив все члены неравенств на v (обозначим х1 = q1/v, х2 = q2/v, x3= q3/v, заметим, что
v= 1/(x1 + x2+x3)).
Итак, задача принимает вид:
18x1+11x2+7x3 ≤ 1
19x1+14x2+11x3 ≤ 1
15x1+13x2+19x3 ≤ 1
f = x1+x2+x3 → max
Таким образом, получена пара двойственных задач. Напомним, что решив одну из них, например, симплекс-методом, мы автоматически найдем решение другой.
Получено оптимальное решение в соответствии с рисунком 11.
х1 = 0,05, х2 =0, х3= 0,01
v = 1/(x1 + x2 + x3) = 0,06
q1 = 0,0003, q2 = 0, q3 = 0,0006
Расчеты выполняются в среде EXCEL

Рисунок 11 – Результат задачи
Вывод: чтобы обеспечить гарантированный средний проигрыш 0,06 игроку В нужно с вероятностью 0,0003 выбрать первую стратегию и с вероятностью 0,0006 – третью стратегию (или так- чередовать стратегии 1 и 3 в соотношении 1:2).
Игры с природой
Издатель обратился в отдел маркетинга, чтобы выяснить предполагаемый спрос на книгу.
Исследования показали: предполагаемый спрос в ближайшие четыре года (штук): 2000, 3000, 4000 или 5000.
Вероятности спроса (соответственно): 0,1+ 0,005*16; 0,5; 0,2; 0,2 – 0,005*16.
Доход от реализации книги составит (100 + 16 ) руб. за книгу. Если книга не продастся, убытки составят (50- 0,5*16) руб. за книгу. Если издатель не удовлетворит спрос, убытки (упущенная выгода) составят (10 + 0,5*16) руб. за книгу.
Используя, по очереди, различные критерии принятия решений в условиях неопределенности и риска определить, сколько книг должно быть издано в расчете на четырехлетний период.
Вероятности спроса (соответственно): 0,18; 0,5; 0,2; 0,12.
Доход от реализации книги составит 116 руб. за книгу. Если книга не продастся, убытки составят 42 руб. за книгу. Если издатель не удовлетворит спрос, убытки (упущенная выгода) составят 18 руб. за книгу.
Используя, по очереди, различные критерии принятия решений в условиях неопределенности и риска определить, сколько книг должно быть издано в расчете на четырехлетний период.
 неопределенность
решение неопределенность
решение 
| 2 | 3 | 4 | 5 |
| 2 тыс. книг | 116*2 | 116*2-18 | 116*2-18*2 | 116*2-18*3 |
| 3 | 116*2-42 | 116*3 | 116*3-18 | 116*3-18*2 |
| 4 | 116*2-42*2 | 116*3-42 | 116*4 | 116*5-18 |
| 5 | 116*2-42*3 | 116*3-42*2 | 116*4-42 | 116*5 |
 неопределенность
решение неопределенность
решение 
| 2 | 3 | 4 | 5 |
| 2 тыс. книг | 232 | 214 | 196 | 178 |
| 3 | 190 | 348 | 330 | 312 |
| 4 | 148 | 306 | 464 | 562 |
| 5 | 106 | 264 | 422 | 580 |
1. Критерий крайнего оптимизма.
 = 580- выпускать книги в количестве 5 тыс.
= 580- выпускать книги в количестве 5 тыс.
2. Критерий Вальда.
 = 190- выпускать книги в количестве 3 тыс.
= 190- выпускать книги в количестве 3 тыс.
3. Критерий Гурвица.

Пусть коэффициент пессимизма λ равен 0,6.
Тогда  =max(0,6*178+0,4*232; 0,6*190+0,4*348; 0,6*148+0,4*562; 0,6*106+0,4*580) = max(199,6; 253,2; 313,6; 295,6) = 313,6. Т.е. выпускать книги в количестве 4 тыс.
=max(0,6*178+0,4*232; 0,6*190+0,4*348; 0,6*148+0,4*562; 0,6*106+0,4*580) = max(199,6; 253,2; 313,6; 295,6) = 313,6. Т.е. выпускать книги в количестве 4 тыс.
4. Критерий Сэвиджа.
Матрица потерь (рисков).
 неопределенность
решение неопределенность
решение 
| 2 т. (0,18) | 3 (0,5) | 4 (0,2) | 5 (0,12) |
| 2 т. | 0 | 134 | 268 | 402 |
| 3 | 42 | 0 | 134 | 268 |
| 4 | 84 | 42 | 0 | 18 |
| 5 | 126 | 84 | 42 | 0 |
 =84 - издать 4 т. книжек
=84 - издать 4 т. книжек
5. Критерия Лапласа.
Критерий Лапласа является наиболее разумным, логически обоснованным критерием, т.к. учитывает математическое ожидание.
max(232*0,18 + 214*0,5 + 196*0,2 + 178*0,12; 190*0,18 + 348*0,5 + 330*0,2 + 312*0,12; 148*0,18 + 306*0,5 + 464*0,2 + 562*0,12; 106*0,18 + 264*0,5 + 422*0,2 + 580*0,12) = max(41,76+107+39,2+21,36; 34,2+174+66+37,44; 26,64+153+92,8+67,44; 19,08+132+84,4+69,6) = max(209,32; 311,64; 339,88; 305,08) = 339,88, т.е. издать 4 т. книг.
Выводы
Таким образом, в процессе написания курсовой работы были решены следующие задачи:
1. Приобретение практических навыков построения экономико-математических моделей
2. Обучение применению компьютерных технологий при решении задач
3. Обучение постановке экономической задачи и переводу ее на математический язык.
Литература
1. Орлова И.В. Экономико - математическое моделирование.ВЗФЭИ, 2004 г.
2. Розоноэр Л.И. Математические методы решения экономических задач. – М.: МИСИС, 1982 г.
3. Невежин В.Р. Сборник задач по курсу “ ‘Экономико-математическое моделирование “. Москва. 2005 г.
4. Экономико- математические методы и модели. Под ред. Макарова С.И. Москва. 2007.
5. Исследование операций в экономике. Под ред. Кремера Н.Ш. 2007. ЮНИТИ.
6. Хазанова Л.Э. Математическое моделирование в экономике. 1998 г.
7. Полисмаков А.И. Математическая экономика. 2005 г.
8. Лабскер Л.Г. Теория массового обслуживания в экономической сфере. 2008 г.
9. Афанасьев М.Ю. Исследование операций в экономике, Инфра-М., 2009 г.
10. Малыхин В.И. Высшая математика. Инфра-М. 2009.
Дата добавления: 2018-05-12; просмотров: 1969; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
