Извлечение корней комплексных чисел

Комплексные числа и геометрия

СОДЕРЖАНИЕ

ВВЕДЕНИЕ. 3

§ 1. Комплексная плоскость. 4

1.1. Основные понятия и определения. 4

1.2 Примеры.. 7

§ 2. Тригонометрическая форма записи. 14

2.1. Основные понятия и определения. 14

2.2. Примеры.. 14

§3 Произведение в тригонометрической форме. 16

3.1 Основные понятия и определения. 16

3.2 Примеры.. 16

§ 4. Извлечение корней из комплексных чисел. 21

4.1 Основные понятия и определения. 21

§ 5. Показательная форма записи. 23

5.1 Основные понятия и определения. 23

ЗАКЛЮЧЕНИЕ. 25

СПИСОК ЛИТЕРАТУРЫ.. 26

ВВЕДЕНИЕ

Актуальность исследования. Большое значение комплексных чисел в математике и ее приложениях широко известно. Особенно часто применяются функции комплексного переменного. Вместе с тем алгебру комплексных чисел можно успешно использовать в элементарной геометрии, тригонометрии, теории геометрических преобразований, а также в электротехнике и различных задачах с механическим и физическим содержанием.

Метод комплексных чисел позволяет решать планиметрические задачи по готовым формулам прямым вычислением, элементарными выкладками. Выбор этих формул с очевидностью диктуется условиями задачи и ее требованием. В этом состоит простота данного метода, по сравнению с другими методами, ведь готовое решение может быть очень коротким.

В данной работе рассматривается применение комплексных чисел в геометрии.

Объект работы: комплексные числа.

Предмет работы: комплексные числа в геометрии.

Цель работы:исследовать применение комплексных чисел в геометрии.

Основные задачи исследования:

1. изучить комплексную плоскость;

2. определить тригонометрическую форму записи;

3. исследовать произведение в тригонометрической форме;

4. извлечь корни из комплексных чисел;

5. определить показательную форму записи.

Основные методы исследования:изучение литературы по теме, самостоятельное решение задач.

Практическая значимостьпроведённого исследования состоит в том, что в нём подобран материал по теме курсовой работы и решены задачи.

На защиту выносится:теоретический и практический материал по теме исследования.

Курсовая работа состоит из введения, пять параграфов и заключения.

Список литературы содержит 5 наименований.

§ 1§ 1. Комплексная плоскость

Основные понятия и определения

Рассмотрим плоскость и прямоугольную систему координат на ней. Ось абсцисс (ось Ox) обозначим Re z, а ось ординат (ось Oy) обозначим Im z (см. рис 1.1.). Каждому комплексному числу z = x + iy сопоставим точку на этой плоскости с координатами (x, y), и, другими словами, радиус-вектор с координатами (x, y).

Рис. 1.1. Комплексная плоскость z

Заметим, что каждому комплексному числу соответствует только одна точка плоскости, и, наоборот, каждой точке на плоскости соответствует только одно комплексное число.

Длина вектора с координатами (x, y) равна . Таким образом, модуль комплексного числа z = x + iy равен длине вектора, который соответствует данному числу на комплексной плоскости. Часто модуль обозначают |z| = ρ. Несложно проверить, что расстояние между двумя точками комплексной плоскости z₁ и z₂ равно |z₁ − z₂|. Таким образом, модуль разности двух комплексных чисел есть расстояние между точками на комплексной плоскости, которые соответствуют этим числам [4, c. 7-10].

Аргументом комплексного z = x + называется угол ϕ вектором (x, ) и положительным действительной оси z измеряемый хода часовой (рис. 1.2).

Аргумент z обозначается z.

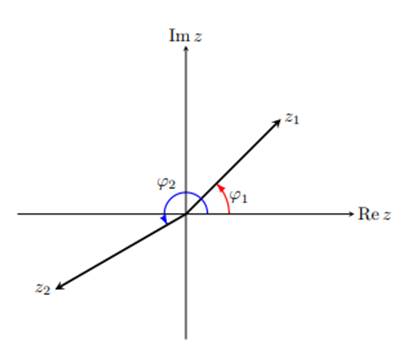
Рис. 1.2. комплексного числа: z₁ = ϕ₁, Arg = ϕ₂

Строго говоря, комплексного числа не однозначно, общем виде можно записать

Arg z = z + 2πk, где ∈ Z, (1.1)

где 0 z < 2π — главное аргумента. В очередь, главное аргумента комплексного определено однозначно ( принимает значения промежутке [0, 2π)).

Единственное число, для значение аргумента определяют, это = 0. Впрочем, это единственное число, которого модуль нулю, поэтому аргумента в случае не проблемой. Также отметить: для чисел (Im = 0) arg z = 0, число положительное, arg z = π, число отрицательное.

сложение чисел и z₂ по правилу векторов (по параллелограмма). Разность −z₂ представляется , конец которого в точке , а начало — точке z₂ (. рис. 1.3).

Рисунок . 1.3. представление суммы разности

Геометрический умножения на единицу i в повороте угол π/2 (или 90⁰). , пусть z = + iy, тогда ·z = − y + . Преобразование (x, ) → (−y, x) — поворот вектора (, y) на π/2 часовой стрелки [2, . 45-46].

Умножение комплексного z = x + на комплексную e^iθ соответствует на угол θ часовой стрелки.

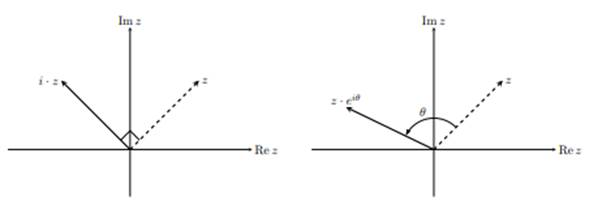
. 1.4. Геометрический смысл на i на e^iθ

смысл операции z → в отражении оси Ox.

1.2

Пример 1. Исходя геометрических рассуждений, неравенство

Решение.

находится на окружности.

Рис. 1.5. дуги больше отрезка.

Построим комплексной плоскости , соответствующий разности − 1 (. 1.5).

Длина дуги окружности, соединяющей 1 и | , равна z и может быть длины отрезка эти точки.

2. Зафиксируем z₀ ∈ и r ∈ , r > 0. Изобразить комплексной плоскости точек, соответствующих числам z, удовлетворяют условиям:

1) | − z₀| = r, 2) | − z₀| r.

1) Пусть z = + iy и = x₀ + iy₀. модуль комплексного |z − z₀| определению:

|z − | = |x + iy − ( + iy₀) | =

|x − + i(y − ) | = )²

Тогда |z − z₀| = равносильно )² = или

(x − ) ² + (y − y₀)² = ².

В свою , уравнение (x − )² + (y − y₀) ² = ² задаёт окружность центром в (x₀, y₀) радиусом r.

2) аналогичным образом, к выводу, неравенство |z − | r равносильно (x − x₀)² + ( − y₀)² r², задаёт круг.

. 1.6. Окружность и с центром точке z₀.

образом уравнения | − z₀| = r |z − z₀| определяют на плоскости окружность круг с в точке и радиусом (рис. 6).

Пример 3. геометрический смысл соотношений:

а) || = Re z + 1, ) |z| = Im + 1.

Решение.

а) z = x + , тогда первое можно переписать

(1.2)

Отметим, модуль комплексного |z| всегда или равен . Поэтому x −1 ( Re z −1).

обе части (1) в квадрат приведём подобные:

= 2x + 1

Уравнение задаёт с вершиной точке (− 1 2 , 0).

б) аналогичные рассуждения, , что второе эквивалентно уравнению

² = 2y + 1, (1.3)

которое задаёт с вершиной точке (0, − ) (см. . 1.7).

Рис. 1.7. Параболы

4. Изобразить множество на комплексной , соответствующих числам, удовлетворяют условию

| − 1| + |z + 1| = 3.

Решение.

z = x + , тогда (3) равносильно

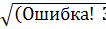+ = 3 (1.4)

Перенесём второе вправо и обе части в квадрат:

( − 1)² + y ² = 9 − 6 + (x + 1)² + y² , (1.5)

, сокращая,

= 9 + 4x. (1.6)

Возведём обе равенства в :

36 (x ² + 2x + 1 + y ² ) = 81 + 2 · 36x + 16x² ,

20x ² + 36y ² = 45.

Перепишем в виде

² /a ² + y ²/ ² = 1,

где a² = 9/4 , = 5/4.

Таким образом, уравнение равносильно уравнению эллипса (. 1.8).

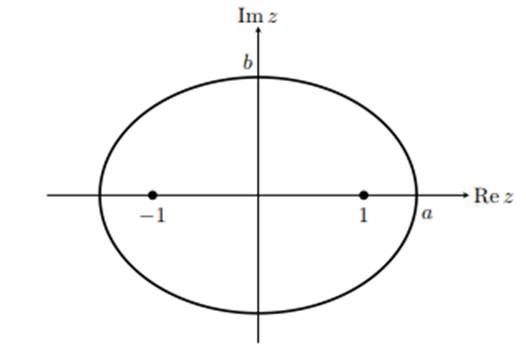
Рис. 1.8. Эллипс ( полуось a = 3/2, полуось b = √5/2 )

. Вообще говоря, самого начала было заметить, уравнение (3) задаёт точек z, которых сумма до двух (−1 и 1) постоянна ( равна 3). Другими , это уравнение с фокусами точках −1 и 1.

5. Найти множество z на плоскости, для выполняется условие | − i| = |z − 1|.

. Заметим, что | −i| — это от z i, а | −1| — расстояние от до 1.

Таким , множество точек , удовлетворяющих, является точек, равноудалённых двух данных ( i и 1).

Это множество собой серединный к отрезку, данные точки (. 1.9).

Рис. 1.9. Серединный к отрезку [1, ]

Пример 6. Для комплексных чисел и w, соотношениям |z| = 12 |w − 3 − 4i| = 5, найти и максимум разности |z − |.

Решение.

Заметим, все числа , удовлетворяющие соотношению || = 12, образуют окружность центром в и радиусом 12. |w − 3 − 4i| = 5 задаёт с центром точке 3 + 4i и 5.

В свою , величина |z − | есть расстояние точками z w.

Таким , задача состоит том, чтобы минимальное и расстояние между z и , лежащими на окружностях. Построим окружности.

Рис. 1.10. |z| = 12 и | − 3 − 4i| = 5

Из рис. 1.10 , что 12 — максимальное , а 2 — минимальное.

Форма записи

Понятия и

Пусть z = + iy и ϕ = z, тогда

ϕ , sin ϕ . (2.7)

Обозначим ρ .

Из (7)

Re z = = ρ cos ϕ и z = y = ρ ϕ. (2.8)

В итоге (1.8) имеем

z = + iy = ρ(cos ϕ + ϕ).

Запись комплексного вида z = ρ( ϕ+isin ϕ), где ρ = ||, а ϕ = Arg , называется тригонометрической.

2.2.

Пример 7. Записать z = 1 + i тригонометрической форме.

Данное число на комплексной является вектором координатами (1, 1).

Вектор по диагонали квадрата, и угол ϕ = π/4. Длина (мо- дуль ) ρ = 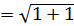= √ 2.

Таким образом,

= √ 2(cos π/ 4 + isin π/ 4 ).

2.11 - Радиусов R r равно − (R + r), одна окружность вне другой, R − (d + ), если одна – другой (d — между центрами).

В тригонометрической

Основные понятия определения

Пусть = ρ₁(cos ϕ₁ + isin ϕ₁), z₂ = ρ₂(cos ϕ₂ + ϕ₂) — два комплексных (в тригонометрической ), тогда несложно , что их можно вычислить образом:

z₁ · = ρ₁ · ρ₂(cos (ϕ₁ + ϕ₂) + isin (ϕ₁ + ϕ₂)) (3.9)

словами, модуль двух комплексных равен произведению этих чисел, аргументов сомножителей аргументом произведения.

свою очередь, комплексных чисел, в тригонометрической , имеет вид

/z₂ = ρ₁/ρ₂ (cos (ϕ₁ − ϕ₂) + (ϕ₁ − ϕ₂)).

Таким образом, частного двух чисел равен модулей этих , разность аргументов и делителя аргументом частного.

3.2

Пример 8. Найти и частное чисел:

z₁ = 3 ( (3π/ 4) + isin ( 3π/ 4)) , z₂ = 2 ( ( − π /2) + isin (− π /2)) .

Решение. формуле умножения чисел в форме получаем

· z₂ = 3 · 2 (cos ( 3π /4 + (− π/ 2)) + ( 3π/ 4 + (− π 2 ))) = 6 · (cos (π/4) + isin (π/ 4)) = 3√ 2 + √ 2.

По формуле получаем

z₁/ = 3/ 2 (cos ( 3π /4 - (− π/ 2)) + isin ( 3π/ 4 - (− π 2 ))) = 3/2 · ( (5π/4) + isin (5π/ 4)) = 3√ 2 + i3 √ 2.

(3.9) для произведения комплексных чисел быть обобщена. частности,

z ² = ρ ² ( 2ϕ + isin 2ϕ),

z ⁻¹ = ρ ⁻¹ ((−ϕ) + isin(−ϕ)).

И любого целого k верно

^k = ρ ^k ( kϕ + isin ) (3.10)

Другими словами, (10) задаёт способ комплексного числа степень.

Пример 9.

(1/2 − i √3/2)¹⁰

Решение.

число 1/2−i √3/2 тригонометрической форме.

1/2 − i √3/2 = 1 · (cos ( − π /3) + (− π /3)) .

Далее по (10) вычисляем:

(cos( − π /3) + ( − π /3)) ¹⁰ = (cos( − 10π /3) + isin ( − 10π /3)) = ( (2π/3) + isin (2π /3)) = − 1/2 + i √3/2

ρ = 1 из выражения (10) формула Муавра:

( ϕ + isin ϕ)^k = kϕ + isin (3.11)

Эту формулу использовать для синусов и кратных углов.

10. Вывести формулы sin 3ϕ и 3ϕ.

Решение.

Запишем (11) в частном (k = 3):

(cos ϕ + ϕ) ³ = cos 3ϕ + isin 3ϕ.

формулу, распишем часть:

(cos ϕ + ϕ) ³ = cos³ ϕ + 3i cos² ϕ ϕ − 3 cos ϕ sin² ϕ − ϕ =

cos³ ϕ − 3 cos ϕ ϕ + i(3 cos²ϕ ϕ − sin³ ϕ).

Таким ,

cos³ ϕ − 3 cos ϕ ϕ + i(3 cos² ϕ ϕ − sin³ ϕ) = cos 3ϕ + 3ϕ.

Приравнивая действительные мнимые части,

sin 3ϕ = 3 cos² ϕ ϕ − sin³ ϕ,

cos 3ϕ = ϕ − 3 cos ϕ sin² ϕ.

11. Вычислить (cos 2ϕ + 2ϕ + 1)ⁿ .

Решение.

следующими тригонометрическими :

1 + cos 2ϕ = 2 cos² ϕ sin 2ϕ = 2 sin ϕ · ϕ.

Тогда имеем

2ϕ + isin 2ϕ + 1 = 2 cos² ϕ + 2isin ϕ · ϕ = 2 cos ϕ(cos ϕ + ϕ). \

Далее с формулы Муавра (3.11) в степень :

(cos 2ϕ + isin 2ϕ + 1)= 2ⁿ · cosn ϕ · (cos + isin nϕ).

12. Пусть n ∈ , z ∈ C, || = 1 и известно, z²ⁿ −1. Проверить, zⁿ/1 + z²ⁿ действительным числом (. е. Im ⁿ/1+z ²ⁿ = 0).

Поскольку |z| = 1,

z = cos ϕ + ϕ,

a по (3.11)

z ⁿ = nϕ + isin и z ²ⁿ = 2nϕ + isin 2nϕ.

Далее, формулы

1 + cos 2ϕ = 2 ϕ и sin 2ϕ = 2 ϕ · cos ϕ,

имеем

1 + 2n = 1 + cos ²nϕ + isin 2nϕ = 2 nϕ + i2 nϕ cos =

2 cos nϕ( nϕ + isin ).

Тогда

zⁿ/1 + = (cos nϕ + nϕ)/ (2 cos (cos nϕ + nϕ)) = 1/ 2 cos .

Извлечение корней комплексных чисел

Понятия и

Тригонометрическая запись чисел оказывается и для корней n- степени.

Напомним, корень n- степени (или ) — комплексное число , для которого условие wⁿ = , т. е. возведении этого в степень мы получим .

Если z 0 , существует n корней n- степени из z:

w_k = cos (ϕ + 2πk)/n + (ϕ + 2πk)/ n ), (4.12)

где = 0, 1, 2, . . . , n − 1 и ϕ = z.

При числа w_k одинаковый модуль ( ) и в вершинах n-угольника ( случая см. . 4.12).

Если n = 2, значения корня на диаметре с центром нуле.

Рис. 4.12. значения

Заметим, в формуле (12) — это арифметический рень из числа, а , определён однозначно.

извлечения корня комплексного числа в следующем. мы будем как от z:

(z) = ,

в каждой (за исключением ) f(z) принимать ровно различных значений. образом, √n является примером функции.

Показательная записи

Основные и определения

ещё одна записи комплексных . Для этой потребуется ввести комплексной экспоненты .

Экспонента e^z примером комплексной комплексного переменного.

экспоненту определяют виде суммы ряда:

e^z = 1 + + z²/2! + z³/3! + · · · = ,

как предел :

e^z = lim_n→∞ (1 + /n)ⁿ .

свойства функции — это

e^z+ = e^z · ^w и (^z ) ^w = (^z)·^w, (14)

z, w ∈ — любые комплексные .

Далее нам формула Эйлера:

ⁱ^ϕ = cos ϕ + ϕ, (5.15)

где ϕ ∈ R — число.

В получаем, что | ^iϕ| = 1

для ϕ ∈ R.

При в формулу (5.15) значений ϕ выводим соотношения:

e ⁰= 1, ^π^i/2 = i, e^πⁱ = −1, ³^π^i/2 = −i, e²^πⁱ = 1,

e ^2πki= 1, где ∈ Z.

Равенство

^iπ + 1 = 0,

связывает собой пять распространённых математических и считается из величайших соотношений.

Пусть ∈ C, ρ = |z| ϕ = arg z, число z записать в

z = ρe^iϕ .

ЗАКЛЮЧЕНИЕ

Известно, сколь широко используются комплексные числа в математике и её приложениях. Особенно часто применяется функции комплексного переменного, в частности, аналитические функции.

В §1 были определены основные понятия комплексной плоскости, и были приведены примеры комплексной плоскости в геометрии.

В §2 были определены основные понятия тригонометрической формы записи, и были приведены примеры тригонометрической формы записи в геометрии.

В §3 были определены основные понятия произведения в тригонометрической форме, и были приведены примеры произведения в тригонометрической форме.

В §4 были определены основные понятия извлечения корней из комплексных чисел.

В §5 были определены основные понятия показательной формы записи.

Подводя итоги курсовой работы можно сказать, что поставленная цель достигнута.

СПИСОК

1. Маркушевич А. . Комплексные числа конформные отображения – .: Государственное издательство -теоретической литературы, 1954. – 52 .

2. Понарин Я. . Алгебра комплексных в геометрических : Книга для математических классов , учителей и педагогических вузов – .: МЦНМО, 2004. - 160 с.

3. Д. От Симсона до Дроз-Фарни, . - №6, 2009. – с. 44-48

4. Яглом . М. Геометрические . Линейные и преобразования. - Государственное технико-теоретической , 1956. – 612 с.

5. Яглом . М. Комплексные и их в геометрии – .: Физматгиз, 1963. – 192 с.

Дата добавления: 2018-05-12; просмотров: 336; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!